СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ С ИСПОЛЬЗОВАНИЕМ СХЕМЫ MIMO В ГИПЕРКОМПЛЕКСНОМ ПРОСТРАНСТВЕ Российский патент 2023 года по МПК H04B7/413 

Изобретение относится к системам передачи информации, в частности способам реализации схемы MIMO [H04B7/0413].

Из уровня техники известен МЕТОД И СИСТЕМА БЕСПРОВОДНОЙ СВЯЗИ MIMO, ИСПОЛЬЗУЮЩИЕ СОВМЕСТНОЕ ПРЕОБРАЗОВАНИЕ АДАМАРА И СХЕМУ АЛАМУТИ (KR20160010799(A), опубл. 28.01.2016) включающий: модулирование данных в цифровые символы, выполнение преобразования Адамара модулированных символов для генерации нового созвездия; и кодирование сгенерированного созвездия с использованием метода Аламути в качестве входных данных. При этом на этапе модуляции модулируется схема QPSK посредством комбинации преобразования Адамара и схемы Аламути. При этом на этапе преобразования объединяются две точки модулированного символа в один символ, при этом используется комбинация преобразования Адамара и схемы Аламути. При этом на этапе преобразования создается новая совокупность путем суммы или разности двух точек с использованием комбинации преобразования Адамара и метода Аламути. При этом система беспроводной связи MIMO содержит: модулятор для модуляции данных в цифровые символы на стороне передачи системы беспроводной связи MIMO; преобразователь для преобразования Адамара модулированного символа для создания нового созвездия; и кодер для кодирования сгенерированного созвездия в качестве входных данных с использованием метода Аламути. При этом модулятор представляет собой систему беспроводной связи MIMO с модуляцией QPSK, использующую комбинацию преобразования Адамара и преобразования Аламути, а преобразователь объединяет две точки модулированного символа в один символ, комбинируя преобразование Адамара и схему Аламути. При этом преобразователь генерирует новое созвездие путем суммирования или вычитания двух точек.

Недостатком аналога является низкая скорость передачи информации.

Также известен СПОСОБ ПЕРЕДАЧИ ДАННЫХ В СИСТЕМЕ СВЯЗИ "MIMO" (RU2553679C2, опубл. 20.06.2015) с использованием пространственно-временным кодированием, в котором используется таблица отображения, которая отображает множество символов на антенны и на ресурсы передачи, которые могут быть временными интервалами или участками полосы частот OFDM. Таблица отображения содержит вложенные первичные сегменты кодов Аламоути, а именно кодирование Аламоути на уровне символов, внутри вторичных сегментов, которые могут содержать кодирование Аламоути первичных сегментов.

Недостатком аналога является низкая скорость передачи информации.

Наиболее близкой по технической сущности СПОСОБ ПЕРЕДАЧИ ДАННЫХ С ИСПОЛЬЗОВАНИЕМ ПРОСТРАНСТВЕННО-ВРЕМЕННЫХ БЛОЧНЫХ КОДОВ (US2008063110 А1,опубл., 13.03.2008) который характеризуется тем, что для передачи данных предоставляется набор из по меньшей мере 2^mnxn матриц, которые представляют собой расширение группы без фиксированных точек. Каждой из 2^m матриц присваивается уникальное двоичное число в диапазоне от 0 до 2^m-1, тем самым обеспечивая идентификацию и отображение данных в соответствии с определенным распределением. Для оптимальной передачи, сопоставленные матрицы рекомендуется отправлять с использованием n антенн, где каждая антенна соответствует одной строке каждой матрицы, что обеспечивает многомерное пространственно-временное кодирование с максимальной полосой пропускания и надежностью передачи данных.

Основной технической проблемой прототипа является ограниченная пропускная способность, так как применение метода пространственно-временных блочных кодов (STBC) в схеме множественного входа и множественного выхода (MIMO) системе требует передачи дополнительной информации для кодирования блоков данных, что приводит к увеличению длительности передачи. Это ограничивает пропускную способность системы и может привести к ухудшению производительности в условиях с ограниченным временем передачи данных. Как следствие низкая скорость передачи информации. Другой технической проблемой прототипа является низкая помехоустойчивость, так как метод пространственно-временных блочных кодов (STBC) может быть чувствительным к помехам и искажениям, особенно в каналах с отрицательной корреляцией между антеннами MIMO. Это может привести к ухудшению качества принимаемых данных и повысить вероятность ошибок при декодировании, как следствие низкая помехоустойчивость.

Задачей изобретения является устранение недостатков аналогов и прототипа.

Техническим результатом изобретения является повышение помехоустойчивости и скорости передачи информации в системах беспроводной и проводной связи.

Указанный технический результат достигается за счет того, что способ передачи информации с использованием схемы MIMO в N=2ⁿ , n= 2, 3, 4 гиперкомплексном пространстве, характеризующийся тем, что поступающие на вход передающего устройства последовательности двоичных импульсов данных, состоящих из нулей и единиц, преобразуются в биполярные импульсы, которые преобразуются в N-мерный информационный вектор, состоящий из N информационных импульсов и образующий гиперкомплексное число в векторном представлении, при этом модуляция на передающей стороне осуществляется путем умножения информационного вектора на гиперкомплексную несущую, представляющую собой гиперкомплексное число в полярной форме с различными N-1 опорными частотами в матричном представлении и выполняющую роль канальной матрицы MIMO канала, при этом многочастотная канальная матрица MIMO раскладывается на сумму одночастотных матриц, которые модулируются отдельно и их результаты складываются, образуя многочастотные элементы N-мерного вектора, при этом модулированные по фазе элементы выходного многочастотного модулированного вектора передаются последовательно во времени или с кодовым разделением, или с частотным разделением, при этом векторы сигнала когерентно демодулируются путём умножения принимаемого вектора на транспонированные базисные матрицы одночастотных матриц, представляющих собой ортогональный базис, а прием поступающего на вход приемника вектора сигнала осуществляется с использованием интегрирования результатов умножения с последующим сложением для каждой одночастотной матрицы ортогонального базиса и принятия решения в решающем устройстве о значении элементов вектора.

В частности, гиперкомплексная несущая представляет собой гиперкомплексное число в полярной форме и в матричном представлении в виде квадратной матрицы NxN с N-1 опорными частотами, комбинации которых образуют 2^N-2 комбинационных частот, и такое же количество одночастотных матриц.

Краткое описание чертежей.

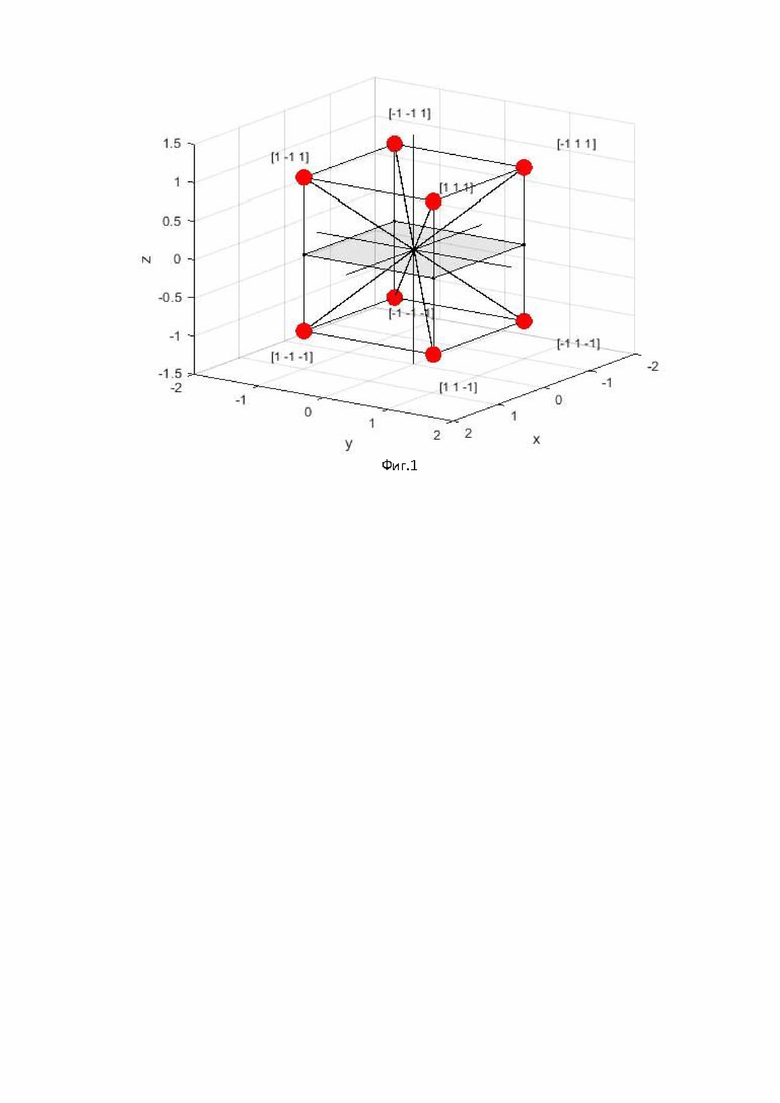
На фиг. 1 показаны векторы информационных импульсов в виде кватерниона для положительного значения первого элемента информационного вектора.

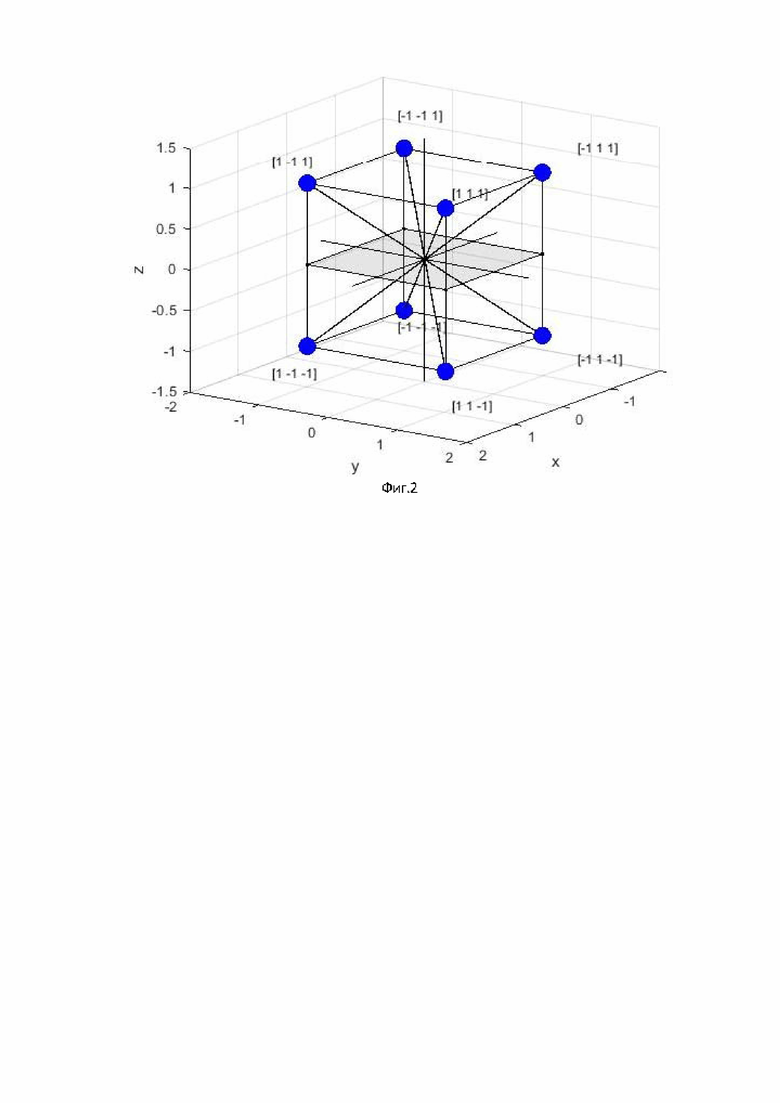
На фиг. 2 показаны векторы информационных импульсов в виде кватерниона для отрицательного значения первого элемента информационного вектора.

На фиг. 3 показан трёхчастотный модулированный по фазе вектор при информационном векторе X0 [11-11] №2.

На фиг. 4 показан трехчастотный модулированный по фазе вектор при информационном векторе X0=[1-1-11] №6.

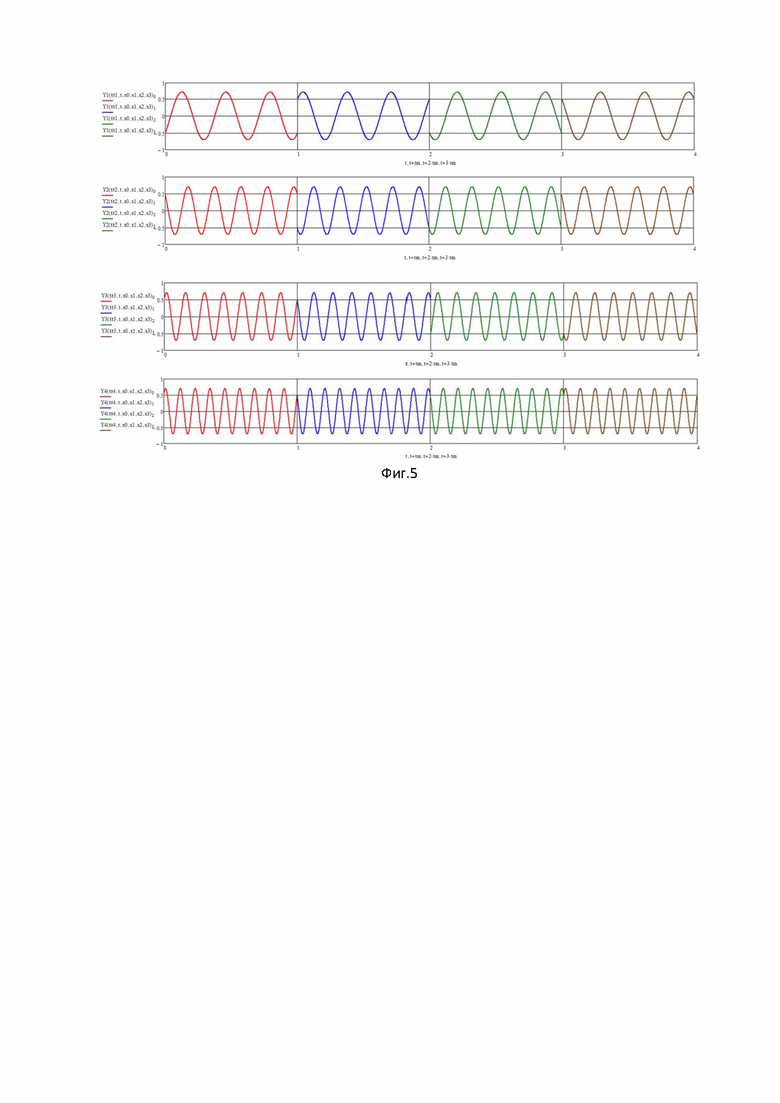
На фиг. 5 показаны одночастотные модулированные по фазе векторы при информационном векторе X0=[11-11] №2.

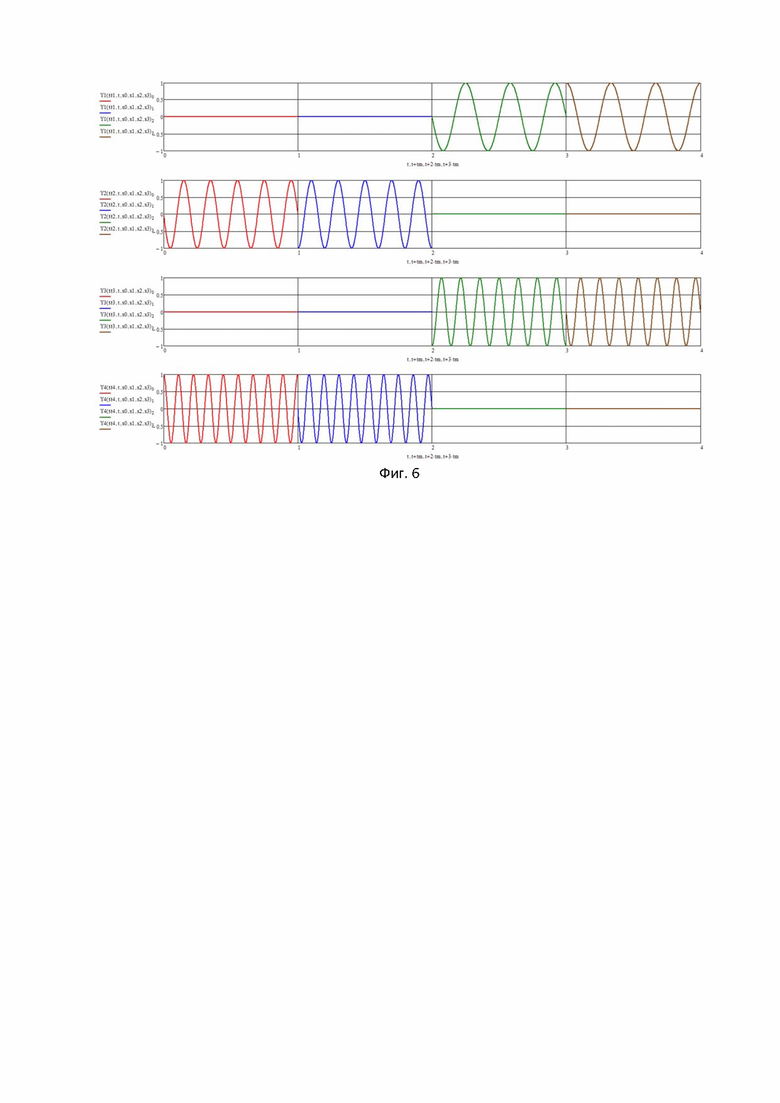
На фиг. 6показаны одночастотные модулированные по фазе векторы при информационном векторе X0=[1-1-11] №6.

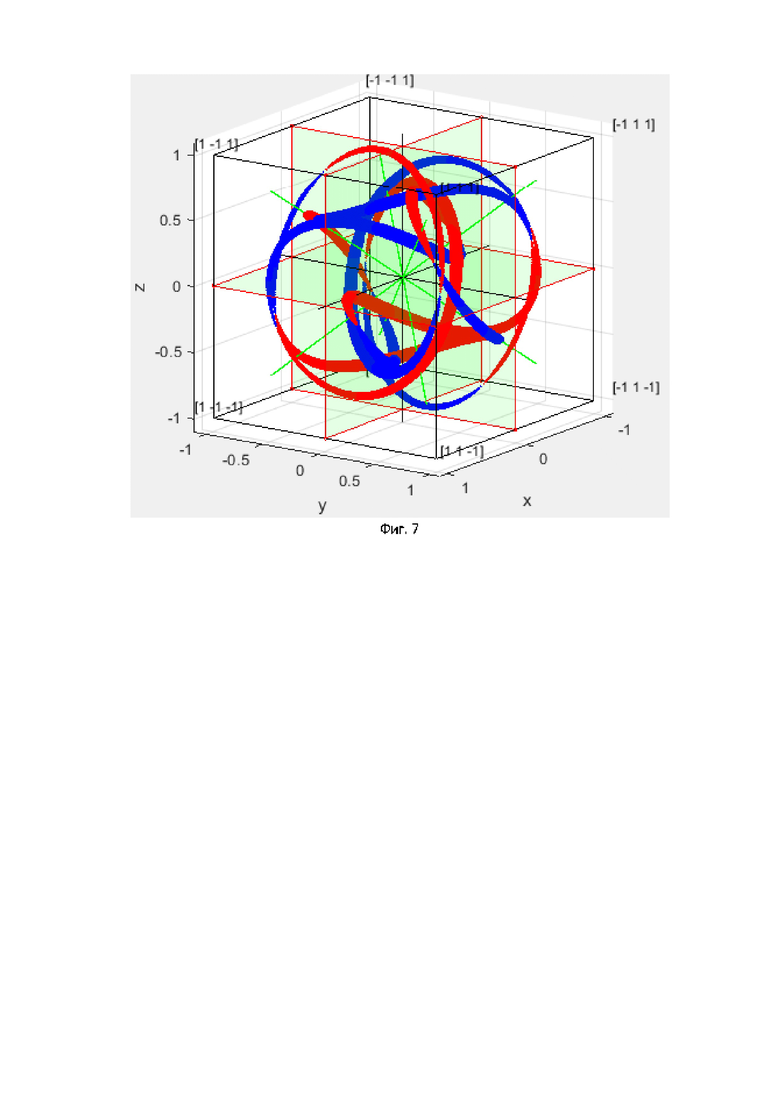
На фиг. 7 показана орбита вращения скалярной части трехчастотного кватерниона для начального вектора X0=[11-11].

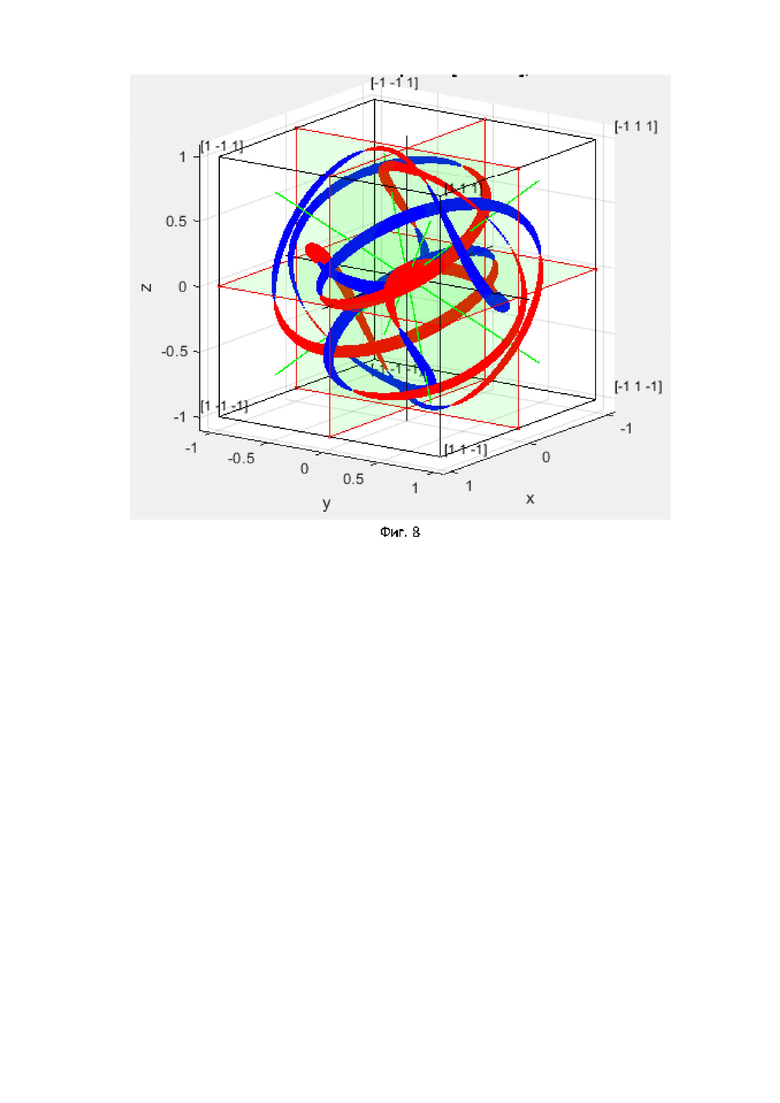
На фиг. 8 показана орбита вращения скалярной части трехчастотного кватерниона для начального вектора X0=[1-1-11].

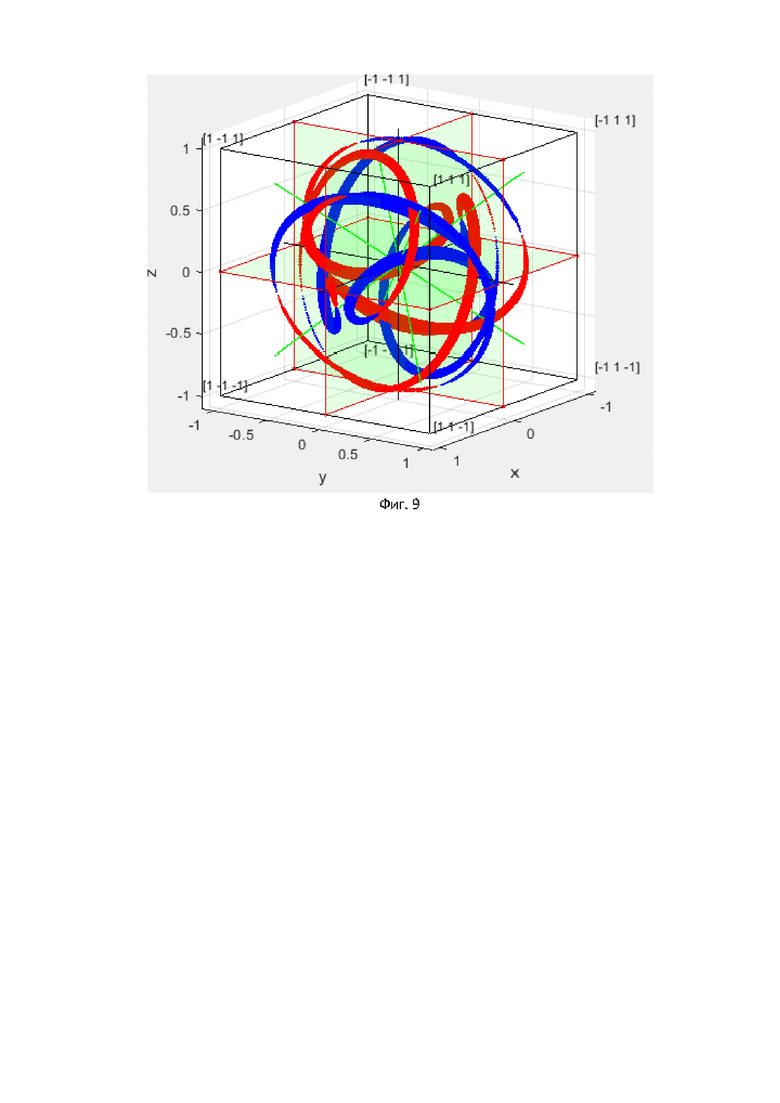
На фиг. 9 показана орбита вращения скалярной части трехчастотного кватерниона для начального вектора X0=[-11-11].

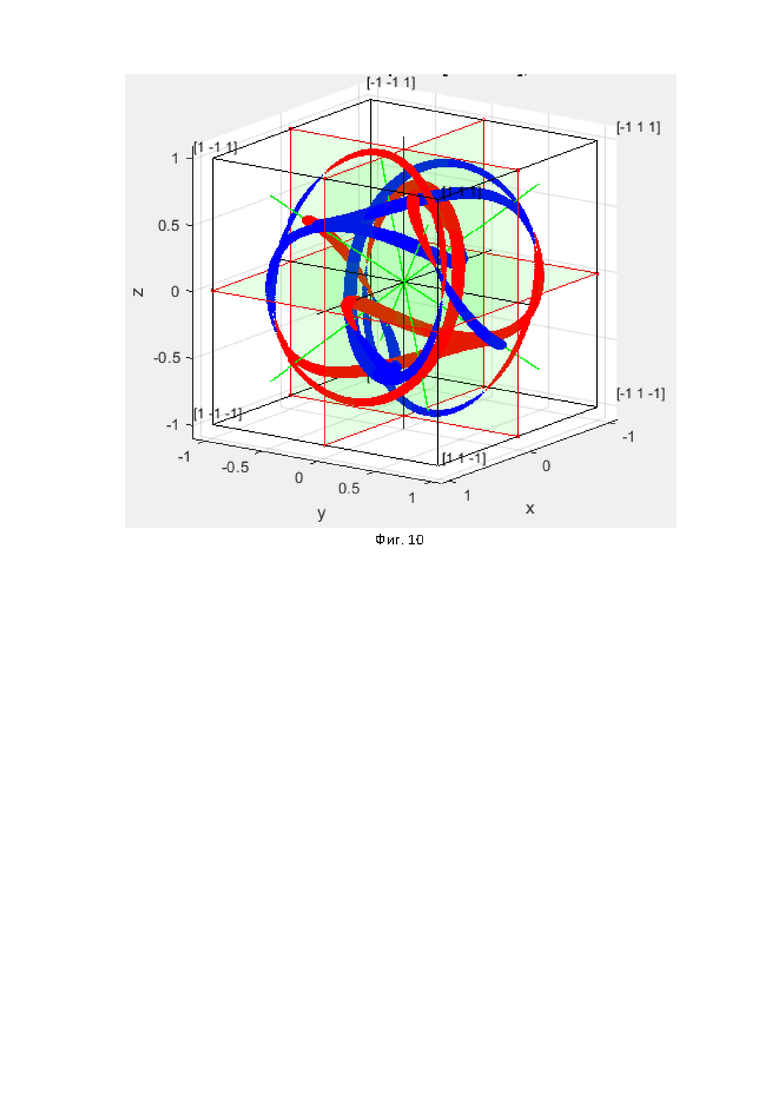
На фиг. 10 показана орбита вращения скалярной части трехчастотного кватерниона для начального вектора X0=[-1-1-11].

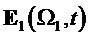
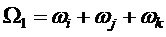
На фиг. 11 показан результат демодуляции по базисной матрице$${\text{E}}_1\left({\Omega }_1,t\right)$$с частотой $${\Omega }_1={\omega }_i+{\omega }_j+{\omega }_k$$.

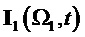
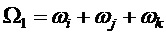
На фиг. 12 показан результат демодуляции по базисной матрице$$I_1\left({\Omega }_1,t\right)$$с частотой $${\Omega }_1={\omega }_i+{\omega }_j+{\omega }_k$$.

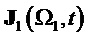
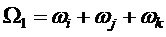
На фиг. 13 показан результат демодуляции по базисной матрице $${\text{J}}_1\left({\Omega }_1,t\right)$$с частотой $${\Omega }_1={\omega }_i+{\omega }_j+{\omega }_k$$.

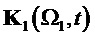
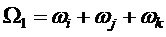
На фиг. 14 показан результат демодуляции по базисной матрице$$K_1\left({\Omega }_1,t\right)$$с частотой $${\Omega }_1={\omega }_i+{\omega }_j+{\omega }_k$$.

На фиг. 15 показана сумма значений по базисным матрицам с частотой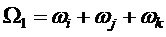$${\Omega }_1={\omega }_i+{\omega }_j+{\omega }_k$$.

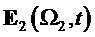
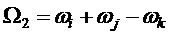
На фиг. 16 показан результат демодуляции по базисной матрице $${\text{E}}_2\left({\Omega }_2,t\right)$$с частотой$${\Omega }_2={\omega }_i+{\omega }_j-{\omega }_k$$.

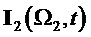
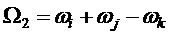
На фиг. 17 показан результат демодуляции по базисной матрице $$I_2\left({\Omega }_2,t\right)$$с частотой $${\Omega }_2={\omega }_i+{\omega }_j-{\omega }_k$$.

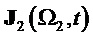
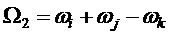
На фиг. 18 показан результат демодуляции по базисной матрице $$J_2\left({\Omega }_2,t\right)$$с частотой $${\Omega }_2={\omega }_i+{\omega }_j-{\omega }_k$$.

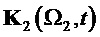
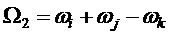
На фиг. 19 показан результат демодуляции по базисной матрице $$K_2\left({\Omega }_2,t\right)$$ с частотой $${\Omega }_2={\omega }_i+{\omega }_j-{\omega }_k$$.

На фиг. 20 показана сумма значений по базисным матрицам с частотой 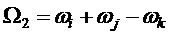$${\Omega }_2={\omega }_i+{\omega }_j-{\omega }_k$$.

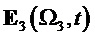
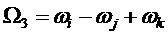
На фиг. 21 показан результат демодуляции по базисной матрице $${\text{E}}_3\left({\Omega }_3,t\right)$$ с частотой $${\Omega }_3={\omega }_i-{\omega }_j+{\omega }_k$$.

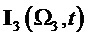
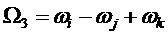
На фиг. 22 показан результат демодуляции по базисной матрице $$I_3\left({\Omega }_3,t\right)$$ с частотой $${\Omega }_3={\omega }_i-{\omega }_j+{\omega }_k$$.

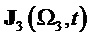
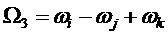
На фиг. 23 показан результат демодуляции по базисной матрице $$J_3\left({\Omega }_3,t\right)$$ с частотой $${\Omega }_3={\omega }_i-{\omega }_j+{\omega }_k$$.

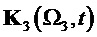
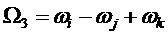
На фиг. 24 показан результат демодуляции по базисной матрице $$K_3\left({\Omega }_3,t\right)$$ с частотой $${\Omega }_3={\omega }_i-{\omega }_j+{\omega }_k$$.

На фиг. 25 показана сумма значений по базисным матрицам с частотой 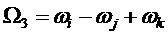$${\Omega }_3={\omega }_i-{\omega }_j+{\omega }_k$$.

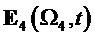
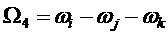
На фиг. 26 показан результат демодуляции по базисной матрице $$E_4\left({\Omega }_4,t\right)$$ с частотой $${\Omega }_4={\omega }_i-{\omega }_j-{\omega }_k$$.

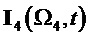
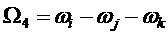
На фиг. 27 показан результат демодуляции по базисной матрице $$I_4\left({\Omega }_4,t\right)$$ с частотой $${\Omega }_4={\omega }_i-{\omega }_j-{\omega }_k$$.

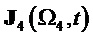
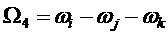
На фиг. 28 показан результат демодуляции по базисной матрице $$J_4\left({\Omega }_4,t\right)$$ с частотой $${\Omega }_4={\omega }_i-{\omega }_j-{\omega }_k$$.

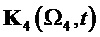
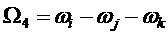
На фиг. 29 показан результат демодуляции по базисной матрице $$K_4\left({\Omega }_4,t\right)$$ с частотой $${\Omega }_4={\omega }_i-{\omega }_j-{\omega }_k$$.

На фиг. 30 показана сумма значений по базисным матрицам с частотой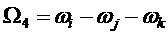$${\Omega }_4={\omega }_i-{\omega }_j-{\omega }_k$$.

На фиг. 31 показана сумма значений по всем частотам.

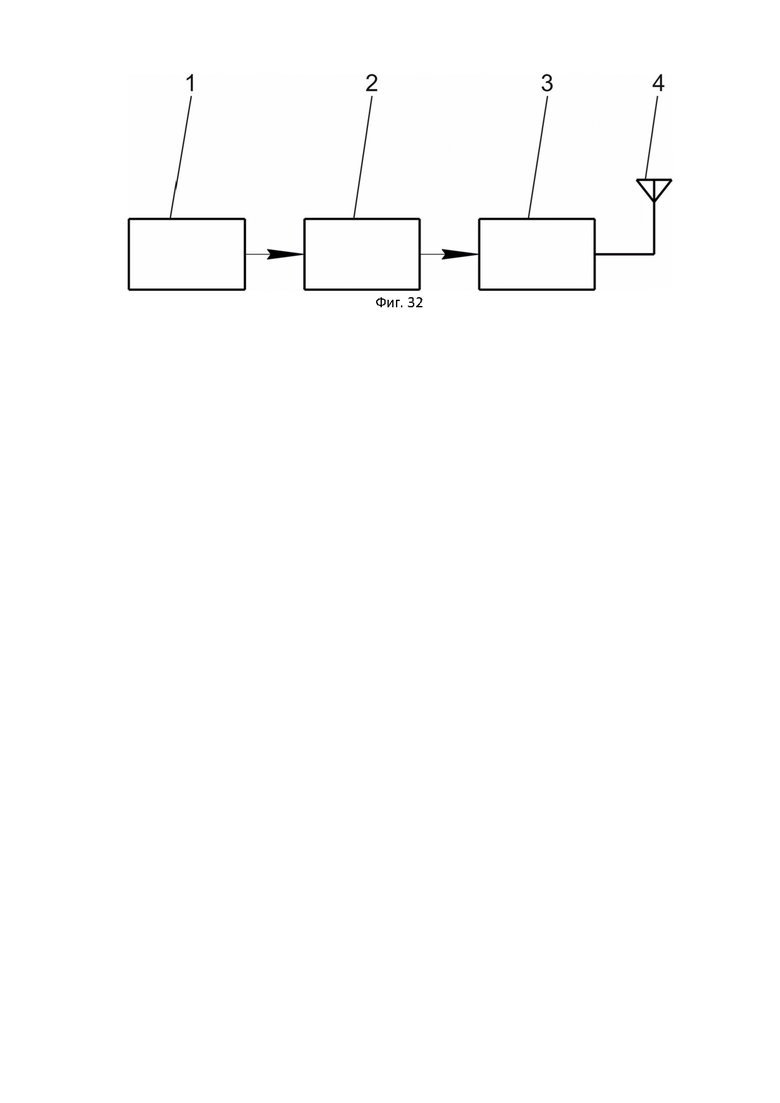
Фиг. 32 показана функциональная блок-схема, демонстрирующая структуру иллюстративного беспроводного передатчика.

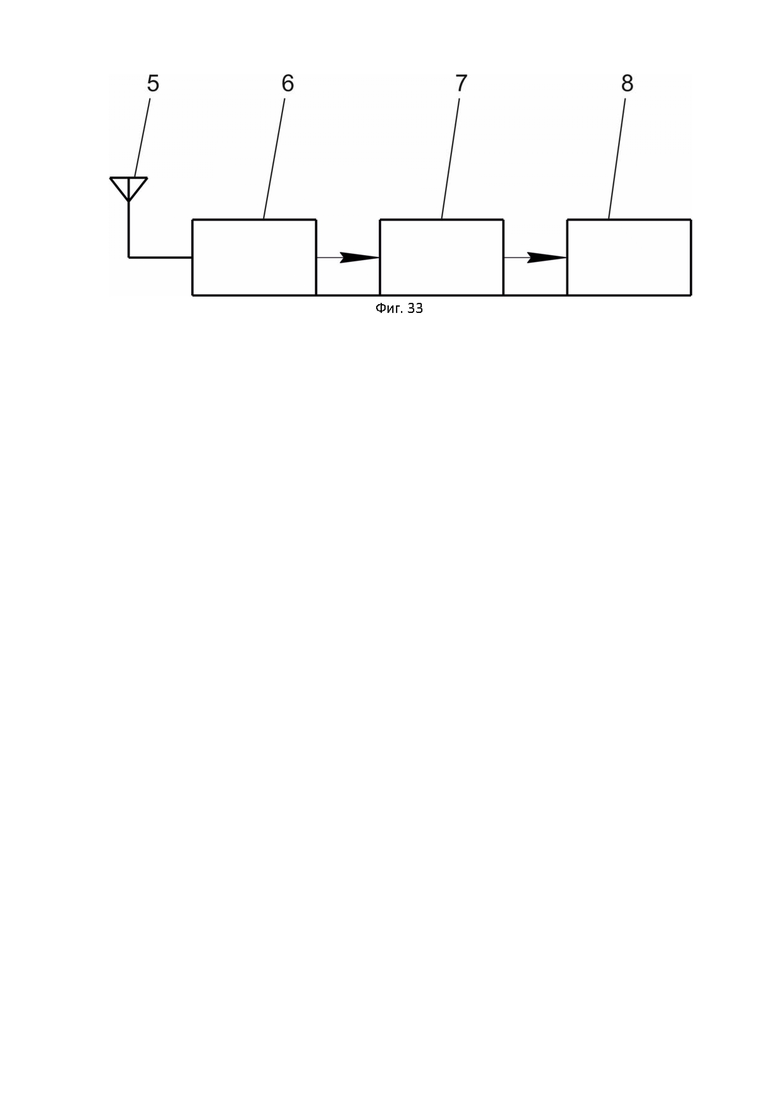
Фиг. 33 показана функциональная блок-схема, демонстрирующая структуру иллюстративного беспроводного приемника.

На фигурах обозначено: 1 –источник информации, 2 – кодер гиперкомлексных чисел, 3 – модулятор гиперкомлексных чисел, 4 – передающая антенна, 5 – принимающая антенна, 6 - демодулятор гиперкомлексных чисел, 7 – декодер гиперкомлексных чисел, 8 – получатель информации.

Осуществление изобретения.

Рассмотрим способ передачи информации с использованием схемы MIMO в гиперкомплексном пространстве при использовании кватерниона.

Кватернион представляет гиперкомплексное число, имеющее три мнимых единицы i, j, k. В алгебраической форме кватернион запишем, как

$$q=s+xi+yj+zk$$ , (1)

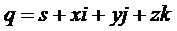
где s, x, y, z – действительные числа.

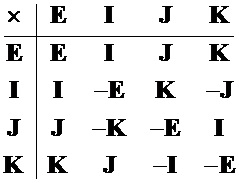
Представим операции с мнимыми единицами в виде таблицы.

Таблица 1. Операция умножения мнимых единиц кватерниона.

$$\begin{array}{ccccc}\times & 1& i& j& k\\ 1& 1& i& j& k\\ i& i& -1& k& -j\\ j& j& -k& -1& i\\ k& k& j& -i& -1\end{array}$$ .

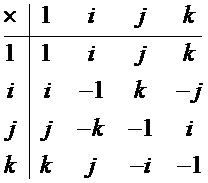
Как известно, в задачах радиотехники и передачи информации используются действительные сигналы, поэтому, чтобы избавиться от мнимых единиц, представим кватернион в алгебраической форме (1) в матричном виде:

$$Q=\left[\begin{array}{cccc}s& x& y& z\\ -x& s& -z& y\\ -y& z& s& -x\\ -z& -y& x& s\end{array}\right]$$ . (2)

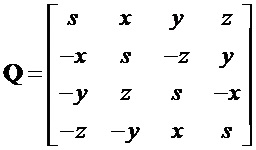
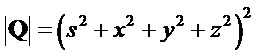
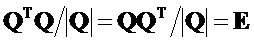
Определитель матрицы$$\left|Q\right|={\left(s^2+x^2+y^2+z^2\right)}^2$$. Матрица Q ортогональная, так как

$$Q^{\mathrm{T}}Q/\left|Q\right|=Q{Q}^{\mathrm{T}}/\left|Q\right|=E$$ .

Мнимые единицы в матричном представлении для матрицы (2) запишем, как

$$I=\left[\begin{array}{cccc}0& 1& 0& 0\\ -1& 0& 0& 0\\ 0& 0& 0& -1\\ 0& 0& 1& 0\end{array}\right]$$ , $$J=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ -1& 0& 0& 0\\ 0& -1& 0& 0\end{array}\right]$$, $$K=\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& -1& 0\\ 0& 1& 0& 0\\ -1& 0& 0& 0\end{array}\right]$$. (3)

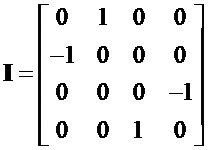
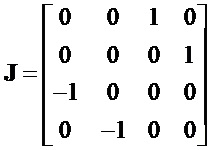
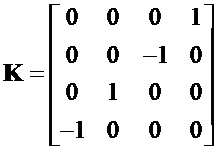
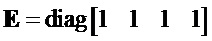
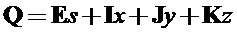
Матрицы мнимых единиц совместно с единичной матрицей с единицами на главной диагонали $$E=\mathrm{diag}\left[\begin{array}{cccc}1& 1& 1& 1\end{array}\right]$$, называют базисными матрицами кватерниона. Матрицу кватерниона (2) записывают с использованием базисных матриц (3) и единичной матрицы E, как

$$Q=Es+Ix+Jy+Kz$$ . (4)

Для базисных матриц (3) справедлива аналогичная Таблице 1 таблица умножения:

Таблица 2. Операция умножения мнимых единиц кватерниона в матричном представлении.

$$\begin{array}{ccccc}\times & E& I& J& K\\ E& E& I& J& K\\ I& I& -E& K& -J\\ J& J& -K& -E& I\\ K& K& J& -I& -E\end{array}$$ .

Для кватерниона (1) запишем экспоненциальную функцию, как

$${\mathrm{e}}^q={\mathrm{e}}^{s+xi+yj+zk}={\mathrm{e}}^s\left(\cos x+i\sin x\right)\left(\cos y+j\sin y\right)\left(\cos z+k\sin z\right)$$ . (5)

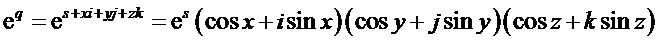
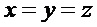
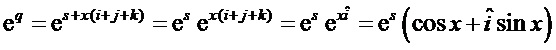
Отметим, что при $$x=y=z$$ выражение (5) примет вид:

$${\mathrm{e}}^q={\mathrm{e}}^{s+x(i+j+k)}={\mathrm{e}}^s{\mathrm{e}}^{x(i+j+k)}={\mathrm{e}}^s{\mathrm{e}}^{x\widehat{i}}={\mathrm{e}}^s\left(\cos x+\widehat{i}\sin x\right)$$ ,

где 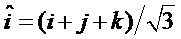$$\widehat{i}=(i+j+k)/\sqrt{3}$$.

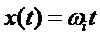
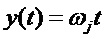
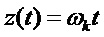
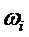
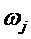
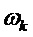
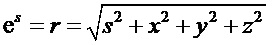
Также, как и для комплексного числа при экспоненциальном отображении, коэффициенты при мнимых единицах кватерниона в полярной форме записи имеют физический смысл угла поворота. Поэтому, запишем углы в (5) как функции времени: $$x(t)={\omega }_{i}t$$, $$y(t)={\omega }_{j}t$$, $$z(t)={\omega }_{k}t$$, где $${\omega }_i$$, $${\omega }_j$$, $${\omega }_k$$ - угловые частоты на осях i, j, k. Будем полагать, что $${\mathrm{e}}^s=r=\sqrt{s^2+x^2+y^2+z^2}$$ - радиус вращения в 4D пространстве.

После перемножения выражений в круглых скобках в формуле (5) и группировки по действительной и мнимым частям, получим экспоненциальную функцию в виде трёхчастотного кватерниона, которую обозначим, как

$$f\left(q(t)\right)=p(t)+iu(t)+jv(t)+kw(t)$$ . (6)

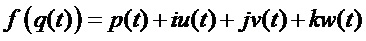
После приведения подобных членов, составляющие в выражении (6) экспоненциальной функции от трёхчастотного кватерниона примут вид:

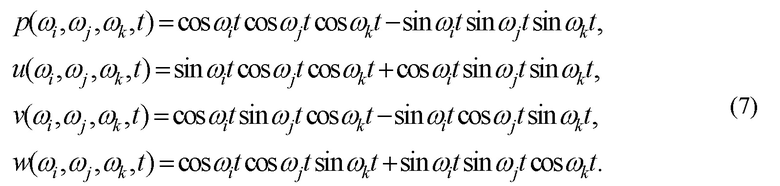
Экспоненциальную функцию от трёхчастотного кватерниона (5) запишем в матричном виде с использование полученных выражений (7), как

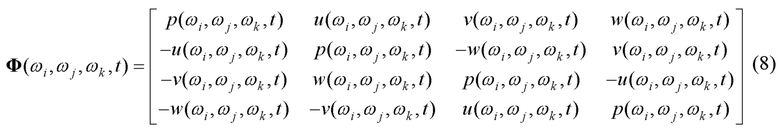
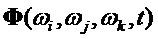
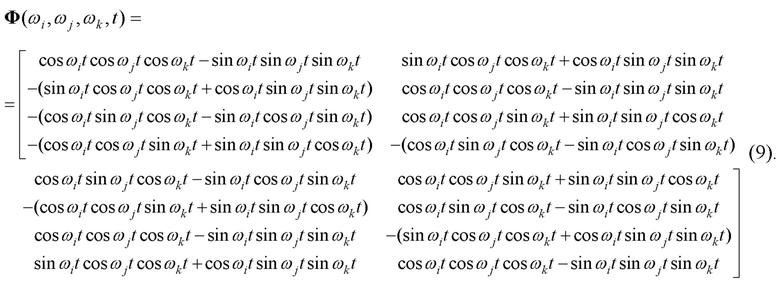
При матричном представлении (8) выражения (6) получим трехчастотную фундаментальную матрицу $$\Phi ({\omega }_i,{\omega }_j,{\omega }_k,t)$$:

Базисные матрицы (9) представим в виде (4):

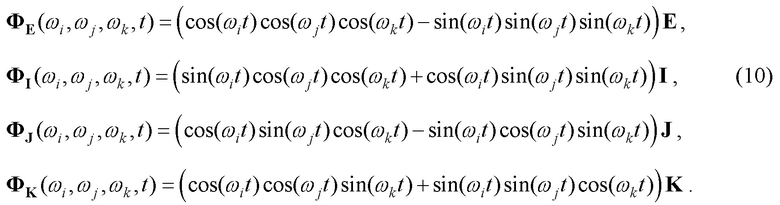
Запишем разложение фундаментальной матрицы (9) по базисным матрицам, как

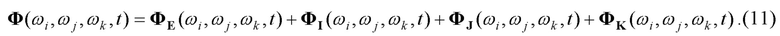
Выражение (5) при единичном радиусе также представим в матричном виде, с использованием одночастотных матриц:

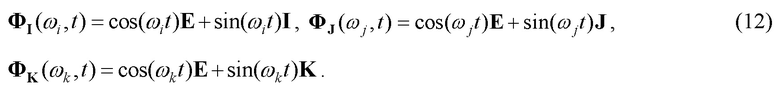
Перемножив одночастотные базисные матрицы (12), получим матрицу (9).

Таким образом, фундаментальную матрицу 3-х частотного кватерниона (9) можно представить в виде суммы базисных 3-х частотных матриц (11) или в виде произведения одночастотных матриц (12).

Рассмотрим основные свойства фундаментальной матрицы трехчастотного кватерниона в виде суммы (11) и произведения (12). Фундаментальная матрица (9) является ортогональной, так как

$${\Phi }^{\mathrm{T}}({\omega }_i,{\omega }_j,{\omega }_k,t)\Phi ({\omega }_i,{\omega }_j,{\omega }_k,t)=\Phi ({\omega }_i,{\omega }_j,{\omega }_k,t){\Phi }^{\mathrm{T}}({\omega }_i,{\omega }_j,{\omega }_k,t)=E$$ .

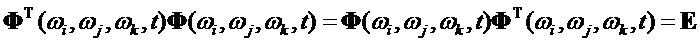
Определитель матрицы (9) вычисляется с использованием (7), как

$$\left|\Phi ({\omega }_i,{\omega }_j,{\omega }_k,t)\right|={\left(p^2({\omega }_i,{\omega }_j,{\omega }_k,t)+u^2({\omega }_i,{\omega }_j,{\omega }_k,t)+v^2({\omega }_i,{\omega }_j,{\omega }_k,t)+w^2({\omega }_i,{\omega }_j,{\omega }_k,t)\right)}^2$$ .

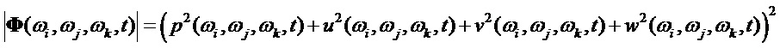
Подставив в формулу определителя выражения (7), получим

$$\left|\Phi ({\omega }_i,{\omega }_j,{\omega }_k,t)\right|=E$$ .

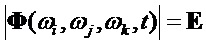
Определитель произведения базисных одночастотных матриц (12) равен определителю 3-х частотной матрицы (9):

$$\left|{\Phi }_I({\omega }_i,t){\Phi }_J({\omega }_j,t){\Phi }_K({\omega }_k,t)\right|=\left|\Phi ({\omega }_i,{\omega }_j,{\omega }_k,t)\right|$$ .

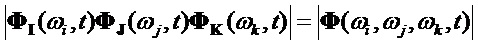
Согласно известному свойству произведения определителей, определитель произведения одночастотных фундаментальных матриц для разных частот равен произведению определителей этих матриц:

$$\left|{\Phi }_I({\omega }_i,t){\Phi }_J({\omega }_j,t){\Phi }_K({\omega }_k,t)\right|=\left|{\Phi }_I({\omega }_i,t)\right|\left|{\Phi }_J({\omega }_j,t)\right|\left|{\Phi }_K({\omega }_k,t)\right|$$ .

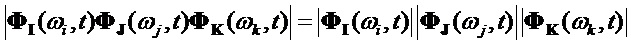
Отсюда,

$$\left|\Phi ({\omega }_i,{\omega }_j,{\omega }_k,t)\right|=\left|{\Phi }_I({\omega }_i,t)\right|\left|{\Phi }_J({\omega }_j,t)\right|\left|{\Phi }_K({\omega }_k,t)\right|=$$

$$={\left({\cos }^2({\omega }_{i}t)+{\sin }^2({\omega }_{i}t)\right)}^2{\left({\cos }^2({\omega }_{j}t)+{\sin }^2({\omega }_{j}t)\right)}^2{\left({\cos }^2({\omega }_{k}t)+{\sin }^2({\omega }_{k}t)\right)}^2=1$$ .

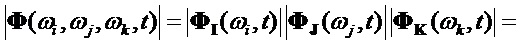
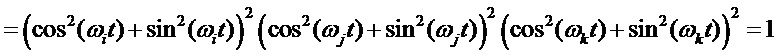
Как видно из (10), мы получили 8 комбинаций произведений косинусов и синусов разных частот. Используем для преобразования выражений (7) известные формулы тригонометрии для произведений трёх комбинаций с синусами и косинусами. Согласно этим формулам, произведения трех синусов и косинусов в различных сочетаниях преобразуются в сумму синусов и косинусов от суммы частот в различных сочетаниях. Обозначим полученные в результате разложения комбинации угловых частот, как

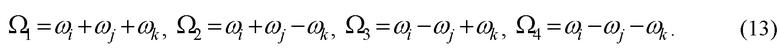
Соответствующая матрица преобразования опорных частот в комбинационные имеет вид:

$$\Omega =\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& -1\\ 1& -1& 1\\ 1& -1& -1\end{array}\right]$$ . (14)

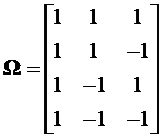
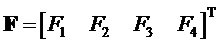
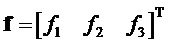
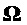
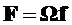
Соответствующие комбинационные частоты получаем в виде вектора $$F={\left[\begin{array}{cccc}{F}_1& F_2& F_3& F_4\end{array}\right]}^{\mathrm{T}}$$ путем умножения вектора опорных частот $$f={\left[\begin{array}{ccc}{f}_1& f_2& f_3\end{array}\right]}^{\mathrm{T}}$$ на матрицу $$\Omega$$:$$F=\Omega f$$.

Матрица преобразования комбинационных частот в опорные вычисляется из (14), как

$$\frac{1}{4}{\Omega }^{\mathrm{T}}=\frac{1}{4}\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 1& -1& -1\\ 1& -1& 1& -1\end{array}\right]$$ .

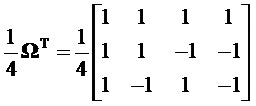
Рассмотрим пример:

$$f=\left[\begin{array}{c}6\\ -2\\ -1\end{array}\right]$$ , $$F=\Omega f=\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& -1\\ 1& -1& 1\\ 1& -1& -1\end{array}\right]\left[\begin{array}{c}6\\ -2\\ -1\end{array}\right]=\left[\begin{array}{c}3\\ 5\\ 7\\ 9\end{array}\right]$$.

$$f=\frac{1}{4}{\Omega }^{\mathrm{T}}F=\frac{1}{4}\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 1& -1& -1\\ 1& -1& 1& -1\end{array}\right]\left[\begin{array}{c}3\\ 5\\ 7\\ 9\end{array}\right]=\left[\begin{array}{c}6\\ -2\\ -1\end{array}\right]$$ .

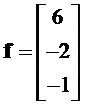
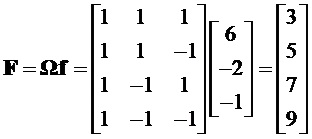
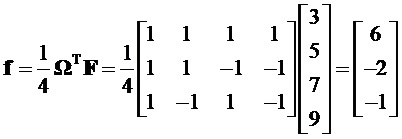
После вычисления произведений синусов и косинусов в (10) с использованием указанных формул тригонометрии, приведения подобных членов и группировки по частотам, получим следующие выражения для экспоненциальных функций (10) для комбинационных частот (13):

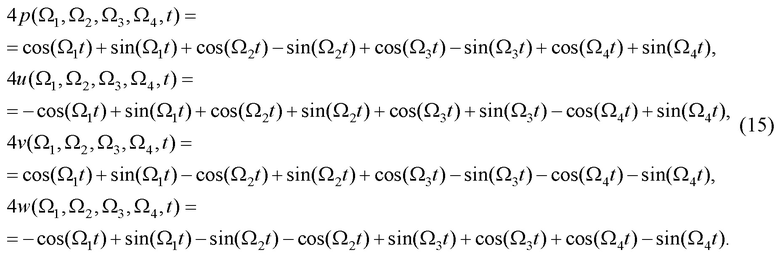
Подставив выражения (15) для комбинационных частот в матрицу произведений (12) и сгруппировав члены по частотам, получим представление фундаментальной матрицы в виде суммы одночастотных матриц:

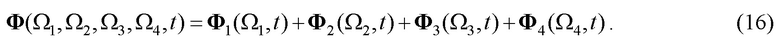
Где

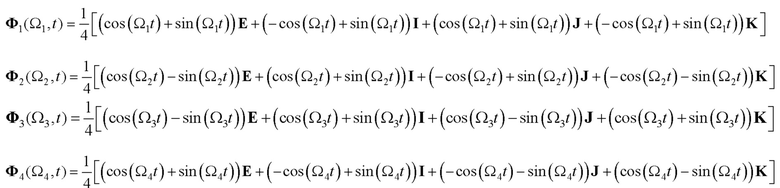
Соответствующие нормированные базисные матрицы для комбинационных частот обозначим, как

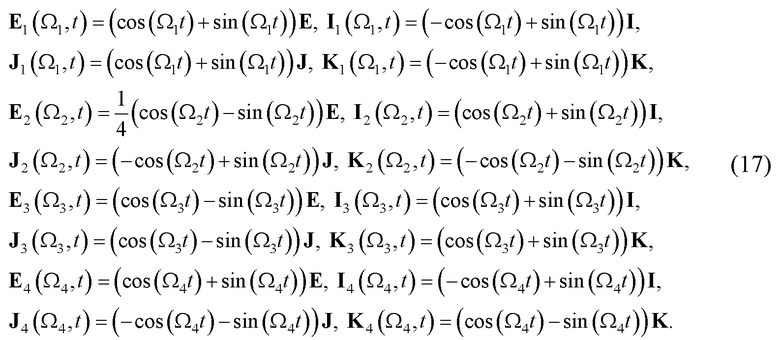
В процессе корреляционного приема при интегрировании произведений базисных матриц на соответствующие транспонированные матрицы (17) на длительности T=1 получим, что

$$E_m{}^{\mathrm{T}}\left({\Omega }_m,t\right)E_m\left({\Omega }_m,t\right)=E$$ , $$I_m{}^{\mathrm{T}}\left({\Omega }_m,t\right)I_m\left({\Omega }_m,t\right)=E$$, $$J_m{}^{\mathrm{T}}\left({\Omega }_m,t\right)J_m\left({\Omega }_m,t\right)=E$$,

$$K_m{}^{\mathrm{T}}\left({\Omega }_m,t\right)K_m\left({\Omega }_m,t\right)=E$$ ,

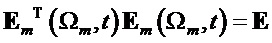
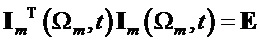
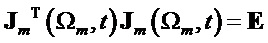
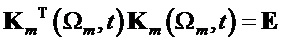
где m=1, 2, 3, 4.

Таким образом, мы получили выражения для экспоненциальной функции (5) трехчастотного кватерниона в виде суммы функций (6), которые представляются 8 комбинациями произведений косинусов и синусов опорных частот (7). Также, с использованием формул тригонометрии для произведений трёх комбинаций с синусами и косинусами, получили экспоненциальную функцию (5) в виде сумм косинусов и синусов (15) различных комбинаций частот (13).

Манипуляция многочастотной матрицы.

Возможные комбинации двоичных символов представим в виде векторов начальных состояний, записанных в матрицу:

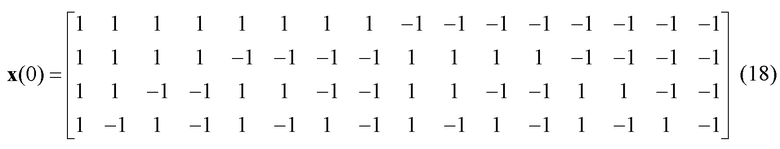
Амплитуда информационных векторов равна

$$A=\sqrt{x_0^2+x_1^2+x_2^2+x_3^2}=\sqrt{\pm 1^2\pm 1^2\pm 1^2\pm 1^2}=\sqrt{4}=2$$ .

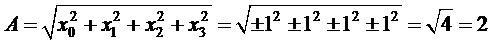
Мощность информационных векторов равна

$$P=x_0^2+x_1^2+x_2^2+x_3^2=\pm 1^2\pm 1^2\pm 1^2\pm 1^2=4$$ .

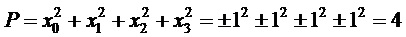
Трехчастотную фундаментальную матрицу (9) будем использовать в качестве канальной матрицы MIMO канала в математической модели системы передачи информации. При использовании несущей частоты опорные частоты будут сдвинуты на величину несущей, образуя спектры на положительных и отрицательных опорных частот. Так как при приеме сигналов на несущей частоте происходит обратное преобразование, то будем рассматривать канальную матрицу на опорных и комбинационных частотах.

Манипуляцию запишем в виде умножения вектора начальных состояний на трехчастотную фундаментальную матрицу опорных частот, которую определим по аналогии с методами модуляции сигналами, рассматриваемыми на действительной оси или плоскости, как «кватернионную несущую», в общем случае – «гиперкомплексную несущую»:

$$y({\omega }_i,{\omega }_j,{\omega }_k,t)=\Phi ({\omega }_i,{\omega }_j,{\omega }_k,t)x(0)$$ . (19)

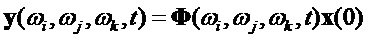
В результате умножения, получим модулированный вектор выхода 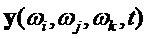$$y({\omega }_i,{\omega }_j,{\omega }_k,t)$$.

Так как многочастотная матрица равна сумме одночастотных матриц (16), то манипуляция по одночастотным матрицам будет, соответственно, иметь вид:

$$y({\omega }_i,{\omega }_j,{\omega }_k,t)=\left[{\Phi }_1({\Omega }_1,t)+{\Phi }_2({\Omega }_2,t)+{\Phi }_3({\Omega }_3,t)+{\Phi }_4({\Omega }_4,t)\right]x(0)$$ . (20)

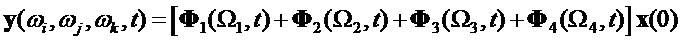
Запишем (20) в виде отдельных векторов выхода:

$$y_1({\Omega }_1,t)={\Phi }_1({\Omega }_1,t)x(0)$$ , $$y_2({\Omega }_2,t)={\Phi }_2({\Omega }_2,t)x(0)$$, $$y_3({\Omega }_3,t)={\Phi }_3({\Omega }_3,t)x(0)$$, (21)

$$y_4({\Omega }_4,t)={\Phi }_4({\Omega }_4,t)x(0)$$ .

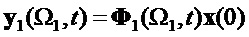
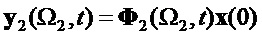
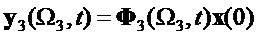
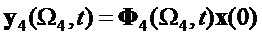
Возможные комбинации информационных векторов (18) изобразим в виде состояний в 3D пространстве, как показано на фигурах 1 и 2. На фиг.1 в узловых точках показаны положительные значения старшего разряда информационного вектора, на фиг.2 в узловых точках показаны отрицательные значения старшего разряда информационного вектора.

Элементы вектора (19) могут передаваться с использованием различного вида разделения: кодового, частотного или по времени.

На фигурах 3 и 4 показаны графики выходного вектора (19) с последовательной передачей во времени для опорных частот 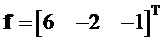$$f={\left[\begin{array}{ccc}6& -2& -1\end{array}\right]}^{\mathrm{T}}$$ для двух возможных комбинаций векторов начального состояния. Отрицательная частота для синуса означает просто смену знака амплитуды.

Так как фундаментальная матрица (9) ортогональная и не изменяет норму информационного вектора, то мощности элементов выходного вектора равны 1.

На фигурах 5 и 6 показаны графики элементов выходных векторов (21) для четырех одночастотных матриц при двух комбинациях информационных векторов.

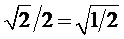
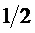
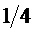
При 4-х ненулевых значениях элементов амплитуда будет $$\sqrt{2}/2=\sqrt{1/2}$$, мощность с учетом коэффициента $$1/2$$ для гармоники получим $$1/4$$.

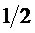
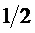
Амплитуда элементов векторов выхода одночастотных матриц может быть A=1 для 2 элементов и 0 для других 2-х элементов. Мощность элемента с учетом коэффициента $$1/2$$ для гармоники будет$$1/2$$, т.е. мощность 1 элемента будет в 2 раза меньше.

В сумме по элементам мощность вектора будет 1 для элементов векторов на фигуре 5 и на фигуре 6. Мощность одного вектора одночастотной матрицы будет 1. Для 4 векторов по одночастотным матрицам мощность будет равна 4.

Таким образом, мощность выходного вектора будет равна мощности входного вектора по многочастотной и в сумме по одночастотным матрицам.

На фигурах 7 и 8 показаны графики орбит вращения скалярной части кватерниона для различных начальных нормированных к 1 векторов с положительной скалярной частью, представляющую старший разряд двоичного вектора.

На фигурах 9 и 10 показаны графики орбит вращения скалярной части кватерниона для тех же начальных нормированных к 1 векторов с отрицательной скалярной частью, представляющую старший разряд двоичного вектора.

Всего получим 8 орбит для положительного значения скалярной части и 8 орбит для отрицательной скалярной части. Данные орбиты сгруппируем по одинаковым траекториям и запишем как номера информационных векторов (18):

1, 6 и11,16 2,3 и 14,15 4, 7 и 10, 13 5, 8 и 9,12.

Как видно, всего имеем 4 различных конфигураций траекторий для четырех различных информационных векторов. При воздействии помех в виде 4D вектора белого шума с центральной симметрией помехи будут не коррелированы даже при условии одинаковой траектории, так как начальные состояния располагаются в разных местах траектории.

Известно, что для одночастотного кватерниона имеются также 4 траектории вращения скалярной части. Однако эти траектории располагаются на плоскостях в 3D. Для трехчастотного кватерниона, так как вращение для 4 комбинационных частот будет с разной скоростью, то траектория будет более сложной и в 3D траектории охватывают намного большее 3D пространство и, как следствие, сигналы имеют существенно большее разнообразие. Как известно, чем больше разнообразие сигнала, тем он меньше подвержен воздействию помех и тем больше скорость передачи информации возможно получить. В предельном случае, когда сигнал похож на белый шум и занимает весь объем, получим пропускную способность MIMO канала. Отметим также, что мощность, а, следовательно, и длина вектора вращения, остается постоянной.

Проходя по каналу связи, к модулированным колебаниям из комбинационных частот добавляются помехи. В качестве помехи рассмотрим 4D белый шум с циркулярной симметрией. В результате получи вектор сигнала с помехой:

$$s(t)=\left[\begin{array}{c}{y}_1({\Omega }_1,{\Omega }_2,{\Omega }_3,{\Omega }_4,t)\\ y_2({\Omega }_1,{\Omega }_2,{\Omega }_3,{\Omega }_4,t)\\ y_3({\Omega }_1,{\Omega }_2,{\Omega }_3,{\Omega }_4,t)\\ y_4({\Omega }_1,{\Omega }_2,{\Omega }_3,{\Omega }_4,t)\end{array}\right]+\left[\begin{array}{c}{n}_1(t)\\ n_2(t)\\ n_3(t)\\ n_5(t)\end{array}\right]$$ .

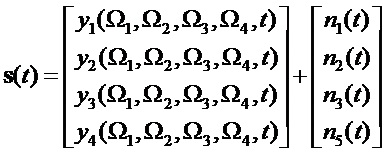
Так как в качестве помехи рассматривается белый шум, то оптимальным приемником для каждого элемента является коррелятор.

Демодуляцию принимаемого вектора будем производить по нормированным транспонированным базисным матрицам (17) по каждой одночастотной матрице отдельно, в которых комбинационные частоты заменим на опорные в соответствии с (13).

Умножение принимаемой последовательности элементов вектора $$s(t)$$ на элементы базисных матриц и их интегрирование с последующим суммированием результатов осуществляется в реальном масштабе времени без задержки импульсов. В конце накопления энергии сигнала производится отсчет, который запоминается. Так как каждый элемент последовательности $$s(t)$$ содержит все элементы информационного вектора, то при умножении его на элементы столбцов базисных матриц получим оценки всех четырех информационных элементов. В последующем, все отсчеты каждого элемента по всем базисным матрицам каждой одночастотной матрицы складываются и подаются на решающее устройство.

На фигурах 11-30 показаны результаты умножения принятого вектора на базисные матрицы одночастотных матриц после интегрирования на длительности импульсов.

На фигуре 31 показана сумма результатов по матрицам 4-х частот.

При приеме элементов выходного вектора (19) путем умножения на базисные ортогональные матрицы норма вектора не изменяется. Однако при этом осуществляется перестановка элементов вектора помехи в соответствии со структурой матриц E, I, J, K. Следовательно, при сложении элементов векторов они складываются по энергии, а элементы вектора помех складываются по мощности. Поэтому, для каждой матрицы мы получаем выигрыш в отношении сигнал/шум, по сравнению с приёмом действительных сигналов с BPSK, в 4 раза. Так как прием одних и тех же значений осуществляется на разных частотах, то общий выигрыш в отношении сигнал/шум при некоррелированности помех и при достаточном разносе частот для устранения их влияния друг на друга будет равен 16, если не считать увеличение полосы частот. Обычно при работе в высокочастотных диапазонах волн увеличение полосы не ведет за собой каких-либо больших издержек.

Техническим результатом изобретения является повышение помехоустойчивости и скорости передачи информации в системах беспроводной и проводной связи, который достигается за счет того, что поступающие на вход передающего устройства последовательности двоичных импульсов данных, состоящих из нулей и единиц, преобразуются в биполярные импульсы, которые преобразуются в N-мерный информационный вектор, состоящий из N информационных импульсов и образующий гиперкомплексное число в векторном представлении, при этом обеспечивается большее энергетическое расстояние (в сравнение с физическим пространством, пространственно-временным кодом), а также эффективное использование N-мерного гиперкомплексного пространства гиперкомлексного числа по времени и частоте, увеличение помехоустойчивости передаваемой информации, как следствие, достигается повышение скорости передачи информации.

При этом модуляция на передающей стороне осуществляется путем умножения информационного вектора на гиперкомплексную несущую, представляющую собой гиперкомплексное число в полярной форме с различными N-1 опорными частотами в матричном представлении и выполняющую роль канальной матрицы MIMO канала, при этом многочастотная канальная матрица MIMO раскладывается на сумму одночастотных матриц, которые модулируются отдельно и их результаты складываются, образуя многочастотные элементы N-мерного вектора, при этом модулированные по фазе элементы выходного многочастотного модулированного вектора передаются последовательно во времени или с кодовым разделением, или с частотным разделением, тем самым достигается снижение количества передающих и принимающих антенн за счет использования одной антенны на передаче и одной антенны на приеме, при этом использование N-мерного гиперкомплексного пространства и вращение информационных элементов при модуляции кватернионной несущей позволяет максимизировать энергетическое расстояние между информационными элементами, что приводит к улучшенной помехоустойчивости, большей скорости передаваемой информации, эффективному использованию частотных ресурсов и повышенной скрытности передачи информации, как следствие достигается повышение помехоустойчивости и скорости передачи информации.

При этом, так как канальная матрица MIMO канала – ортогональна, то норма информационного вектора до передачи данных через канал связи будет равна норме информационного вектора после передачи, если канал не изменяет ее, как следствие достигается повышение помехоустойчивости и скорости передачи информации.

При этом выигрыш в отношении сигнал/шум при использовании одночастотной кватернионной канальной матрицы, по сравнению с приемом действительных сигналов с BPSK, в 4 раза и в 16 раз для 4-х частотной канальной матрицы комбинационных частот.

При этом мощность выходного вектора будет равна мощности входного вектора по многочастотным и в сумме по одночастотным матрицам, таким образом, система передачи информации сохраняет мощность сигнала на каждой частоте или в каждом отдельном канале, как следствие:

1. Эффективно используются ресурсы: нет избыточной потери энергии или резких изменений мощности (пикфактор) на разных частотах. Это позволяет оптимально использовать мощность усилителей передатчика и доступную пропускную способность канала связи;

2. Подавление интерференции: Поскольку каждый информационный импульс передается на каждой позиции во времени и на каждой частоте модулированного сигнала и мощность сигнала сохраняется на всех частотах и всех позициях во времени, то система может быть более устойчивой к внешней интерференции. Интерференция на одной частоте не будет влиять на мощность сигнала на других частотах и позициях во времени. Это особенно важно в случае многолучевого распространения (multipathfading) или наличия других источников интерференции, а также при селективных по частоте и по времени замираниях;

3. Поддержка качественной передачи информации: Поскольку мощность сигнала не меняется, сохраняется качество переданных данных. Это особенно важно для передачи аналоговых или цифровых сигналов, где изменение мощности может привести к искажению данных;

4. Удобство обработки: когда мощность входного вектора равна мощности выходного, обработка сигнала становится более предсказуемой и удобной. Нет необходимости корректировать или компенсировать различия в мощности сигнала на разных частотах.

Как следствие достигается повышение помехоустойчивости и скорости передачи информации.

При этом общий выигрыш в отношении сигнал/шум при некоррелированности помех будет равен 16, если не считать увеличение полосы частот.

При этом помехи на ортогональном базисе не коррелируемы, как следствие:

1. Улучшенная разделимость сигналов: помехи можно более эффективно отделить от желаемых сигналов;

2. Улучшенное качество приема: Помехи не суммируются или не усиливаются друг с другом. Это означает, что сигналы могут быть приняты с меньшим искажением и потерей качества. Некоррелированные помехи не создают интерференцию на основных частотах передачи информации;

3. Повышенная безопасность: Помехи, которые не коррелируют, затрудняют или делают более сложной задачу несанкционированного доступа или взлома системы связи. Некоррелированные помехи могут затруднить или сделать невозможным извлечение конфиденциальной информации из передаваемого сигнала;

4. Более эффективное использование радиочастотного спектра: Некоррелированные помехи могут быть лучше изолированы и подавлены при использовании радиочастотного спектра. Это позволяет эффективно использовать доступные частотные полосы, минимизировать взаимное влияние сигналов и помех.

Как следствие достигается повышение помехоустойчивости и скорости передачи информации.

При этом векторы сигнала когерентно демодулируются путём умножения принимаемого вектора на транспонированные базисные матрицы одночастотных матриц, представляющих собой ортогональный базис, а прием поступающего на вход приемника вектора сигнала осуществляется с использованием интегрирования результатов умножения с последующим сложением для каждой одночастотной матрицы ортогонального базиса и принятия решения в решающем устройстве о значении элементов вектора. При этом достаточно вычислить фазу несущего колебания с использованием обычных методов синхронизации и не требуется знание фазы от каждой передающей антенны к каждой приемной антенне, чтобы определить параметры пространственно-временного кода. Обычно для получения таких данных используется обратная связь, пилот-сигнал и сложное вычислительное устройство. Таким образом, реализуется технологии раздельного приёма информационных элементов по базисным матрицам кватерниона, как следствие:

1. Улучшенная спектральная эффективность: увеличение отношения сигнал/шуми возможности передачи информации с большей скоростью;

2. Увеличение помехоустойчивости приема;

3. Повышенная скрытность передачи данных, так как каждый информационный символ содержится в каждом символе передаваемого вектора и тем или иным образом изменяет его параметры модуляции. Поэтому, не зная канальную матрицу и её частоты, невозможно выделить информационные символы.

При этом реализуется возможность проводить оценку каждого элемента информационного вектора при воздействии различных помех, так как помехи раскладываются на составляющие на ортогональном базисе, а при узкополосном спектре не действуют на информационные элементы, передаваемые на других частотах.

Как следствие достигается повышение помехоустойчивости и скорости передачи информации.

При этом гиперкомплексная несущая представляет собой гиперкомплексное число в полярной форме и в матричном представлении в виде квадратной матрицы NxN с N-1 опорными частотами, комбинации которых образуют 2^N-2 комбинационных частот, и такое же количество одночастотных матриц.

При использовании многочастотных гиперкомплексных несущих, в общем случае, или, в частном случае, трёхчастотных кватернионных несущих, модулированные сигналы имею большее разнообразие, т.е. занимают больший объем гиперкомплексного пространства, как показано на фигурах 7-10. Как следствие, они в меньшей степени подвержены помехам, которые отличаются от белого шума и сосредоточены по времени (импульсные помехи) или по частоте (узкополосные помехи).Так как при воздействии помехи типа «белый шум» пропускная способность определяется разностью разнообразия сигнала и энтропии помехи, то при использовании гиперкомплексного многочастотного пространства возможно достичь более высокого разнообразия сигнала, чем при обычных методах модуляции действительных сигналов на плоскости, даже при увеличении числа уровней амплитуд сигналов или частот. Как следствие, существенно повышается пропускная способность таких каналов.

Согласно фиг. 32 и 33 Источник информации 1 преобразует поступающие на вход двоичные импульсы 0, 1 в биполярные 1, -1 и из них образует, в общем случае, N-мерный информационный вектор путем соответствующей задержки импульсов. При этом последний импульс поступает без задержки.

Кодер гиперкомплексных чисел 2 формирует, в общем случае, гиперкомплексную многочастотную несущую в виде NxN матрицы, в частном случае – кватернионную несущую в виде 4х4 матрицы с тремя частотами. Гиперкомплексная несущая представляет собой экспоненциальное отображение гиперкомплексного числа в матричном представлении, которая, в свою очередь, раскладывается на сумму одночастотных матриц.

Модулятор гиперкомплексных чисел 3 осуществляет модуляцию гиперкомплексной несущей путем умножения одночастотных матриц на информационный вектор с последующим сложением результатов для получения модулированного многочастотного колебания, в частном случае, четырехчастотного колебания.

На передающую антенну 4 поступают модулированные сигналы на несущей частоте и усиленные усилителем мощности. Антенна 4 излучает их в заданном направлении.

Приемная антенна 5 усиливает принимаемый сигнал, который далее поступает на малошумящий усилитель и переносится на частоты гиперкомплексной несущей.

Демодулятор гиперкомплексных чисел 6 осуществляет корреляционный приём в реальном времени принимаемых модулированных элементов вектора путем умножения его на элементы в столбцах транспонированных базисных матриц одночастотных матриц комбинационных частот с последующим интегрированием и сложением результатов.

Декодер гиперкомплексных чисел 7 суммирует результаты корреляционного приема по всем многочастотным матрицам, в частном случае, по всем 4-х частотным матрицам трехчастотного кватерниона и подает их на решающее устройство. Решение может приниматься по каждому информационному элементу вектора отдельно или с вычислением нормы Фробениуса.

Получатель информации 8 преобразует биполярные импульсы 1,-1 в 0, 1 и подает их потребителю в требуемом представлении.

Пример реализации.

Заявляемый способ был реализован для кватерниона с использованием канальной матрицы 4х4. В качестве источника данных применен генератор М-последовательности на JK-триггерах с обратной связью. Для формирования 4-х мерного вектора данных из поступающих импульсов первый импульс задерживался с помощью D-триггеров на 3 такта, 2-й - на 2, третий на 1, а 4-й принимался без задержки в реальном масштабе времени.

Трехчастотная канальная матрица опорных частот представлялась в виде суммы 4-х одночастотных матриц комбинационных частот. Для формирования одночастотных канальных матриц использовался высокочастотный генератор, который выдавал на выходе два сдвинутые на π/2 гармонические колебания комбинационных частот, которые образовывали сумму косинуса и синуса с разными знаками в соответствии со структурой канальной матрицы. Модуляция осуществлялась путем перемножения вектора данных на элементы столбцов четырех одночастотных канальных матриц с использованием 4-х перемножителей для каждой матрицы. На один вход перемножителей подавался сигнал с генератора несущей заданной частоты, а на другой – соответствующий элемент вектора импульсов. Результаты, полученные на выходах перемножителей для матриц разных комбинационных частот, суммировались в сумматорах, в результате чего получался 4-х мерный вектор многочастотного сигнала. Описанная процедура соответствует перемножению 4-х мерного информационного вектора на трехчастотную матрицу опорных частот кватернионной несущей.

Перемножение информационного вектора на каждый столбец осуществлялось за один такт длительности информационного импульса и полученный импульс в виде суммы 4-х комбинационных частот переносился на несущую частоту и передавался последовательно во времени через усилитель мощности в антенну. При этом каждый элемент передавался с использование всей мощности усилителя мощности.

Проходя по каналу связи к сигналу добавлялся шум. Для получения характеристик помехоустойчивости на вход приемника дополнительно подавался шум с генератора шума.

Принятый сигнал переносился на исходные комбинационные частоты и принимался с использованием корреляторов. В качестве опорных частот использовались элементы 4-х одночастотных базисных матриц, на которые раскладывались одночастотные матрицы комбинационных частот и представляли собой ортогональный базис.

Все 16 перемножителей с интеграторами для каждой одночастотной матрицы объединялись в шину по 4 в каждом проводе. Демодуляция осуществлялась в реальном времени. При поступлении 1-го элемента он подавался на 1 -й провод шины и умножался на элементы первых столбцов базисных одночастотных матриц. В конце накопления производился отсчет результатов и их суммирование по всем элементам столбца для всех 4-х одночастотных матриц. Результат суммы 16 отсчетов подавался на решающее устройство, которое принимало решение о значении информационного импульса. Вероятность ошибки определялась путем сравнения поданного импульса с принятым. Аналогичные операции производились при поступлении 2-го принимаемого импульса, который подавался на 2-й провод шины и т.д.

Измерение отношения сигнал/шум проводилось с использованием селективного милливольтметра. В результате получили повышение отношения сигнал/шум в 16 раз по сравнению с BPSK и в 8 раз по сравнению со схемой Аламути с MIMO 2х2.

Использование: изобретение относится к системам передачи информации, в частности способам реализации схемы MIMO. Сущность: в способе передачи информации с использованием схемы MIMO в N=2ⁿ, n = 2, 3, 4, гиперкомплексном пространстве, поступающие на вход передающего устройства последовательности двоичных импульсов данных, состоящих из нулей и единиц, преобразуются в биполярные импульсы, которые преобразуются в N-мерный информационный вектор, состоящий из N информационных импульсов и образующий гиперкомплексное число в векторном представлении, при этом модуляция на передающей стороне осуществляется путем умножения информационного вектора на гиперкомплексную несущую, представляющую собой гиперкомплексное число в полярной форме с различными N-1 опорными частотами в матричном представлении и выполняющую роль канальной матрицы MIMO канала, при этом многочастотная канальная матрица MIMO раскладывается на сумму одночастотных матриц, которые модулируются отдельно и их результаты складываются, образуя многочастотные элементы N-мерного вектора, при этом модулированные по фазе элементы выходного многочастотного модулированного вектора передаются последовательно во времени или с кодовым разделением, или с частотным разделением, при этом векторы сигнала когерентно демодулируются путём умножения принимаемого вектора на транспонированные базисные матрицы одночастотных матриц, представляющих собой ортогональный базис, а прием поступающего на вход приемника вектора сигнала осуществляется с использованием интегрирования результатов умножения с последующим сложением для каждой одночастотной матрицы ортогонального базиса и принятия решения в решающем устройстве о значении элементов вектора, при этом гиперкомплексная несущая представляет собой гиперкомплексное число в полярной форме и в матричном представлении в виде квадратной матрицы NxN с N-1 опорными частотами, комбинации которых образуют 2^N-2 комбинационных частот и такое же количество одночастотных матриц. Технический результат: повышение помехоустойчивости и скорости передачи информации в системах беспроводной и проводной связи. 1 з.п. ф-лы, 33 ил.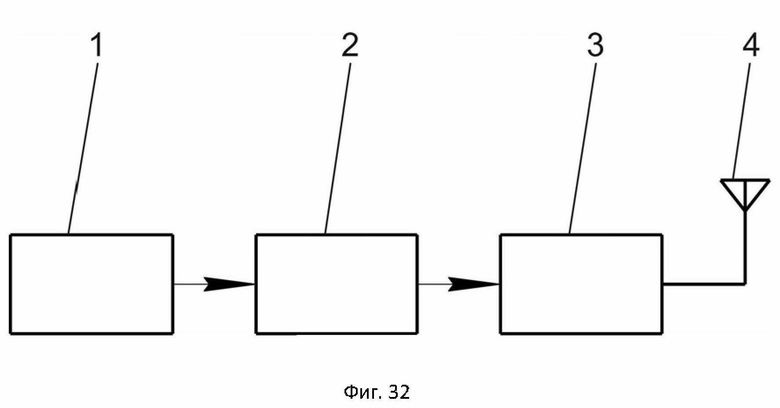

1. Способ передачи информации с использованием схемы MIMO в N=2ⁿ, n = 2, 3, 4, гиперкомплексном пространстве, характеризующийся тем, что поступающие на вход передающего устройства последовательности двоичных импульсов данных, состоящих из нулей и единиц, преобразуются в биполярные импульсы, которые преобразуются в N-мерный информационный вектор, состоящий из N информационных импульсов и образующий гиперкомплексное число в векторном представлении, при этом модуляция на передающей стороне осуществляется путем умножения информационного вектора на гиперкомплексную несущую, представляющую собой гиперкомплексное число в полярной форме с различными N-1 опорными частотами в матричном представлении и выполняющую роль канальной матрицы MIMO канала, при этом многочастотная канальная матрица MIMO раскладывается на сумму одночастотных матриц, которые модулируются отдельно и их результаты складываются, образуя многочастотные элементы N-мерного вектора, при этом модулированные по фазе элементы выходного многочастотного модулированного вектора передаются последовательно во времени или с кодовым разделением, или с частотным разделением, при этом векторы сигнала когерентно демодулируются путём умножения принимаемого вектора на транспонированные базисные матрицы одночастотных матриц, представляющих собой ортогональный базис, а прием поступающего на вход приемника вектора сигнала осуществляется с использованием интегрирования результатов умножения с последующим сложением для каждой одночастотной матрицы ортогонального базиса и принятия решения в решающем устройстве о значении элементов вектора.

2. Способ передачи информации с использованием схемы MIMO в гиперкомплексном пространстве по п.1, отличающийся тем, что гиперкомплексная несущая представляет собой гиперкомплексное число в полярной форме и в матричном представлении в виде квадратной матрицы NxN с N-1 опорными частотами, комбинации которых образуют 2^N-2 комбинационных частот и такое же количество одночастотных матриц.