Область изобретения
Настоящее изобретение относится к отслеживанию и управлению наклоняющимися телами.
Уровень техники, к которой относится изобретение
Известно использование кватернионов для представления ориентации объекта в пространстве. Кватернионная система обозначений, вообще говоря, является более эффективной для использования в вычислительной технике, чем применяемое более широко эйлерово представление данных. Кроме того, кватернионная система обозначений не подвержена сингулярностям, которые могут встречаться при использовании эйлеровой системы обозначений. Следующие патенты США раскрывают использование кватернионов для управления, определения и/или отображения ориентации объекта в пространстве: №5875993; 5212480; 4797836; 4742356 и 4737794.
Общее определение термина “кватернионы”
Кватернион представляет собой гиперкомплексное число с четырьмя элементами, впервые предложенное сэром Уильямом Роуаном Гамильтоном в 1843 г. Кватернион состоит из скалярной части и комплексной векторной части. Векторная часть состоит из упорядоченной тройки (вектора) трех действительных компонент, которым направление присваивается тремя ортогональными комплексными единичными векторами: i, j, k. Ниже приводится пример кватерниона Q в общем виде:
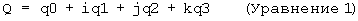
Сложение кватернионов выполняется посредством сложения компонент в аналогичных направлениях. Умножение выполняется с учетом следующих произведений единичных базисных векторов:
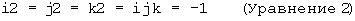



Поскольку кватернион является гиперкомплексным, он также имеет комплексно сопряженный кватернион, в котором направление векторной части изменено на обратное. Ниже приведен пример:
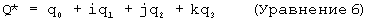
Квадрат величины кватерниона может быть вычислен путем формирования произведения кватерниона с его комплексным сопряжением следующим образом:
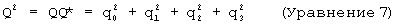
Кватернион единичной величины (Q2=1) имеет специальное значение. В частности, он действует как двусторонний оператор вращения. Полезно заметить, что Гамильтон открыл кватернионы в своих поисках развить трехмерное расширение вращательного эффекта, производимого в комплексной плоскости, когда комплексное число умножается на единичное комплексное число в виде exp(iθ ). Вращательный эффект от exp(iθ ) происходит в результате того, что умножение комплексных чисел требует умножения их соответствующих величин и сложения их соответствующих фаз. Поскольку exp(iθ ) имеет единичную величину, она может только влиять на фазу произведения. В комплексной плоскости это проявляется как вращение относительно начала координат на угол θ . При попытках обобщить данный эффект на векторные вращения Гамильтон первоначально пробовал использовать трехэлементные гиперкомплексные числа. Его попытки были безуспешны до тех пор, пока он не понял, что для того, чтобы учесть изменения "фазы" в трехмерном пространстве, требуется четыре элемента, и тогда он успешно добился требуемого результата.
Обычно векторное вращение выполняется с использованием одностороннего оператора вращения, R, который в трехмерном пространстве может быть представлен в виде действительной ортогональной матрицы размерами 3× 3. Такая матрица преобразования поворачивает вектор х в вектор х' посредством умножения слева следующим образом:
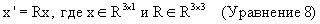
Двусторонний оператор должен применяться, используя умножение и слева, и справа. В случае оператора кватерниона вращение выполняется тогда, когда данный кватернион (X) с нулевой скалярной частью (то есть вектор) умножается сначала слева, а затем справа на единичный кватернион и его сопряженную величину следующим образом:
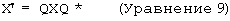
Результирующий вектор, X', поворачивается относительно главной оси на определенный угол, обе компоненты которого определяются единичным кватернионом, Q. Если ось вращения обозначена единичным вектором n, а угол вращения обозначен углом θ , тогда единичные компоненты кватерниона могут быть записаны в виде:
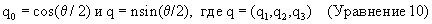
Указанные компоненты удовлетворяют условию нормирования:
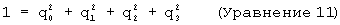
Определенные таким образом компоненты кватерниона также называются эйлеровыми параметрами. Эти параметры содержат всю необходимую информацию для определения оси и угла вращения. Ось вращения, определенная единичным вектором n, также называется собственной осью, поскольку она является собственным вектором односторонней матрицы вращения R, соответствующей собственному значению λ =+1. Это происходит потому, что ось вращения должна быть общей для обоих - исходной и повернутой систем и поэтому не должна изменяться оператором вращения. Заметим, что так называемое вращение собственной оси является единственным вращением относительно главной оси по сравнению с вращением эйлерова угла, которое выполняет то же самое преобразование посредством выполнения трех отдельных вращении: рыскания (поворот вокруг вертикальной оси), тангажа (раскачка относительно поперечной оси) и крена (бокового наклона), относительно осей z, y и х соответственно.
Комплексные единичные векторы кватерниона (i, j, k) связаны со спиновыми матрицами Паули таким образом:
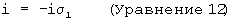
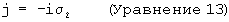
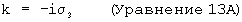
где
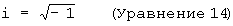
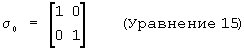
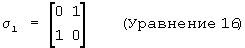
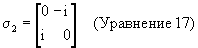
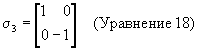
(См.: The Theory of Spinors, E.Cartan (Теория спиноров, Е.Картан))
Используя определения спиновых матриц Паули и единичных кватернионных коэффициентов, единичный кватернион может быть записан следующим образом;
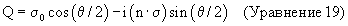
где
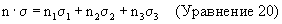
Можно также показать, что оно является эквивалентным следующей матричной экспоненциальной записи:
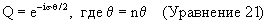
Заметим сходство между данной формой кватерниона и экспоненциальной формой единичного комплексного числа, обсуждавшегося выше. Такая форма предполагает трехмерное изменение в "фазе", которое первоначально искал Гамильтон. Появление половинного угла обусловлено тем, что Q является двусторонним преобразованием. Таким образом, каждый - и левый, и правый множители Q и Q*, вносят половину требуемого пространственного сдвига фазы.
Часто более удобно использовать форму спиновых матриц Паули, чем традиционную гамильтониановскую форму кватерниона. Например, вектор может быть представлен в виде матрицы, посредством формирования внутреннего произведения следующим образом:
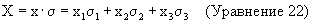
что дает:
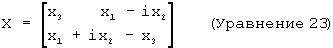
Такая форма матрицы обладает многими полезными свойствами. Например, можно показать, что отражение вектора х плоскостью, определенной посредством единичного вектора нормали а, легко производится, используя матричную форму векторов следующим образом:
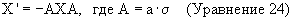
Можно также показать, что любое вращение может быть произведено посредством двух отражений. Если плоскости отражения пересекаются под углом θ /2, а линия пересечения определяется единичным вектором n, то результирующее преобразование повернет любой вектор х относительно собственных осей n на угол θ . Данный факт иллюстрируется ниже, где единичные нормали к плоскостям являются векторами а и b.
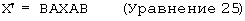
Такой двусторонний оператор, который выполняет вращение, имеет близкое сходство с вращением кватерниона, описанным выше. Действительно, можно показать, что Q=ВА. Следующее мультипликативное тождество следует из свойств матричной формы вектора:
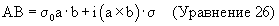
В случае вращения на угол θ единичные нормальные вектора, а и b, должны пересечься под углом θ /2. Поэтому их скалярные и векторные произведения дают a· (b=cos (θ /2) и a× b=nsin(θ /2), где вектор n параллелен линии пересечения. Подстановка этих значений в уравнение 26 дает требуемый результат:
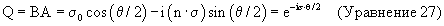
Интересная особенность такого рассмотрения заключается в том, что коэффициенты кватерниона могут быть найдены, используя простые скалярные и векторные произведения соответствующих единичных векторов. В частности, два вектора, а и b, должны быть перпендикулярны к оси вращения и разнесены на угол θ /2. Можно также показать, что если задать координаты двух произвольных векторов α и β в одной системе координат и координаты их повернутых эквивалентов α ' и β ' в повернутой системе координат, то могут быть однозначно определены кватернион и связанная с ним матрица вращения, ответственная за преобразование. Таким образом, задавая два вектора, определенные в базовой системе координат между исходной и двумя внешними опорными точками, пространственное положение системы может быть однозначно определено посредством взятия дополнительных "прицеливаний" для тех же самых двух внешних опорных точек вращаемой системы и сравнения координат опорных векторов, измеренных в конечной системе, с координатами, измеренными в исходной системе.
Можно также рассмотреть, как вычислить компоненты кватерниона прямым интегрированием кватернионной скорости. Такая процедура требует выражения для производной кватерниона как функции угловой скорости. Производная может быть получена дифференцированием уравнения 21. Результирующие производные для каждого из коэффициентов кватерниона являются линейными комбинациями компонент угловых скоростей, взвешенных существующими компонентами кватерниона. Если кватернион и угловые скорости записаны в векторной форме, то получается следующее матричное уравнение:
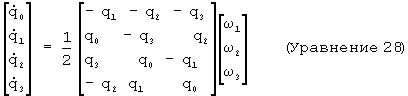
где qi с точкой являются компонентами скорости кватерниона, a ω i являются компонентами угловых скоростей ω (=θ ).
Ориентация и/или вращение тела могут быть представлены более чем в одной системе координат. Например, можно определить систему координат относительно самого тела, представляющего интерес, или определить систему координат относительно внешнего фиксированного объекта. Для некоторых приложений в качестве фиксированного объекта для определения системы координат может быть принята земля. В уравнении 28 угловая скорость отсчитывается по отношению к системе координат, связанной с телом. Аналогичное матричное уравнение, в котором угловая скорость отсчитывается по отношению к системе координат, связанной с землей, приведено ниже - см. уравнение 29. Заметим, что смещение системы отсчета производит несколько изменений знаков в матрице кватернионов.
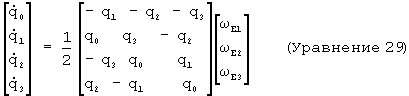
Уравнение 29 может быть записано в более компактной форме, используя матричные переменные, следующим образом:
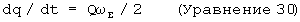
Уравнение 30 может также быть решено для ω Е, как показано ниже, заметив, что QTQ=I:
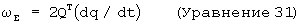
Если уравнение для кватернионной скорости интегрируется, используя мгновенную угловую скорость рассматриваемого тела, результирующий кватернион содержит информацию, необходимую для преобразования координат от исходной системы координат к вращаемой системе. Таким образом, компоненты кватерниона могут использоваться для формирования матрицы вращения R, описанной выше (уравнение 8). Матрица вращения, которая преобразует координаты тела в земные координаты, приводится ниже в терминах кватернионных компонент:
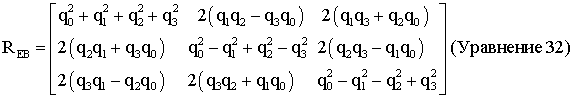
Поскольку матрица преобразований, REB, является ортогональной, ее транспозиция является обратным преобразованием, RBE. Следовательно, кватернионы могут использоваться для отслеживания пространственного положения тела при произвольном угловом движении.
С целью сравнения ниже приводятся уравнения для вычисления эйлеровых угловых скоростей. Соответствующая матрица вращении, R, также приводится как функция эйлеровых углов.
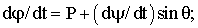
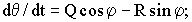
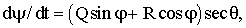
где 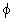 = угол крена;
= угол крена;
θ = угол тангажа;
ψ = угол рыскания;
ω = вектор угловой скорости=[PQR]1;
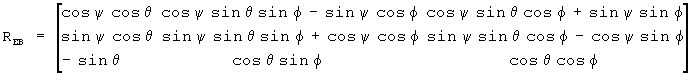
Как известно, способ Эйлера существенно зависит от тригонометрических функций и является весьма интенсивным в вычислительном отношении. Кроме того, скоростные уравнения Эйлера зависят от секанса угла тангажа, что приводит к сингулярности, когда угол тангажа достигает ±90 градусов. Напротив, кватернионный способ не содержит никаких тригонометрических функций и опирается только на операции умножения и сложения. Следовательно, кватернионный способ в вычислительном отношении гораздо более эффективен. Как было отмечено выше, пространственное положение тела может быть однозначно представлено в форме кватерниона, задавая два вектора, определенных в системе координат тела, и две внешних опорных точки. Однако может оказаться трудным и/или дорогостоящим установить две внешних опорных точки, в частности, в случае наземных объектов, расположенных как на земле, так и на или ниже поверхности воды.
Изобретатель настоящего изобретения полагает, что он является первым, кому удалось понять, каким образом можно выгодно модифицировать кватернионную систему обозначений, так, чтобы для получения модифицированной кватернионной формы достаточно было бы использовать только одну внешнюю опорную точку, и что такая модифицированная кватернионная форма может с пользой применяться к телам, которые могут свободно наклоняться, но для которых курс (поворот вокруг вертикальной оси) является ограниченным, или нет необходимости в его управлении системой, использующей модифицированные кватернионы,
Сущность изобретения
Задача изобретения заключается в обеспечении усовершенствованного отслеживания и/или управления наклоняющихся объектов.
Дополнительная задача изобретения заключается в обеспечении системы слежения и системы управления, которые менее требовательны в вычислительном отношении, чем системы из уровня техники.
Также еще задача изобретения заключается в обеспечении применения кватернионной обработки к системе, в которой имеется только одна внешняя опорная координата.
Еще одна задача изобретения заключается в обеспечении надежного отслеживания ориентации объекта в более широкой полосе частот.
Аспект изобретения обеспечивает способ оценки пространственного положения наклоняющегося тела, в котором тело включает устройство, воспринимающее наклон, такое, как жидкостные датчики наклона, а также устройства, воспринимающие угловую скорость, такие, как гироскоп.
Способ включает следующие этапы: выведение информации об угловой скорости из устройств, воспринимающих угловую скорость, преобразование и интегрирование выведенной информации угловой скорости, для формирования первой кватернионной информации положения, так, чтобы первая кватернионная информация положения ограничивалась, чтобы представлять вращение относительно горизонтальной оси в системе координат, связанной с землей, выведение информации наклона из устройств, воспринимающих наклон, обработка выведенной информации наклона для формирования второй кватернионной информации положения, так, чтобы вторая кватернионная информация положения ограничивалась, чтобы представлять вращение относительно горизонтальной оси в системе координат, связанной с землей, сравнение первой кватернионной информации положения для формирования информации о погрешности и использование информации о погрешности для компенсирования дрейфа в устройстве восприятия угловой скорости.
Другой аспект изобретения обеспечивает способ оценки пространственного положения наклоняющегося тела, в котором тело включает устройства, воспринимающие наклон, такие, как жидкостные датчики наклона, а также устройства, воспринимающие угловую скорость, такие, как гироскоп. Способ включает следующие этапы: выведение информации об угловой скорости из устройств, воспринимающих угловую скорость, формирование модифицированной кватернионной информации об угловой скорости из выведенной информации скорости, причем модифицированная кватернионная информация скорости представляется в форме скалярной величины и двухкомпонентного вектора, интегрирование модифицированной кватернионной информации об угловой скорости для формирования первой модифицированной кватернионной информации пространственного положения, при этом этап формирования модифицированной кватернионной информации скорости ограничивается так, чтобы первая модифицированная кватернионная информация пространственного положения была представлена в форме: е=eо+e1i+e2j, где i, j - единичные мнимые векторы, которые удовлетворяют следующим соотношениям друг с другом и с третьим мнимым единичным вектором k: i2=j2=k2=-ijk=-1, ij=-ji=k, jk=-kj=i, ki=-ik=j; выведение информации наклона из устройств, воспринимающих наклон, генерация второй модифицированной кватернионной информации положения из выведенной информации наклона, при этом вторая кватернионная информация положения представляется в форме: е=eо+e1i+е2j, сравнение первой модифицированной кватернионной информации положения со второй модифицированной кватернионной информацией положения для формирования модифицированной кватернионной информации погрешности положения, преобразование модифицированной кватернионнной информации погрешности положения в сигнал ошибки угловой скорости и использование сигнала ошибки угловой скорости для компенсации погрешности в выведенной информации угловой скорости.
При использовании способа, обеспеченного согласно изобретению, информация наклона, выведенная из жидкостного датчика или ему подобного, используется для осуществления компенсации дрейфа или других смещений в датчике угловых скоростей, обладающем широкой полосой пропускания, таком, как набор гироскопов. Компенсация погрешности, обеспеченная через опорные данные наклона, позволяет получить скорректированные широкополосные данные угловой скорости, которые будут интегрироваться для обеспечения оценки отслеживания пространственного положения в реальном масштабе времени, не накапливающую погрешностей смещения. Информация угловой скорости курса (информация угловой скорости рыскания) отбрасывается, чтобы сформировать модифицированное (3-компонентное) кватернионное представление, которое сравнивается с аналогичной модифицированной кватернионной информацией, выведенной из информации наклона и базирующейся на единственной гравитационной опорной точке. Для обеспечения эффективности вычислений компенсация погрешности и фильтрация осуществляются с использованием кватернионной системы обозначений.
Вышеупомянутые аспекты, а также другие аспекты, особенности и преимущества изобретения будут сформулированы и/или очевидны из последующего описания и чертежей. Краткое описание чертежей
В дальнейшем изобретение поясняется описанием конкретных вариантов его воплощения со ссылками на сопровождающие чертежи, на которых:
фиг.1 представляет схематический обобщенный вид сбоку наклоняющегося тела, в отношении которого применяется настоящее изобретение,
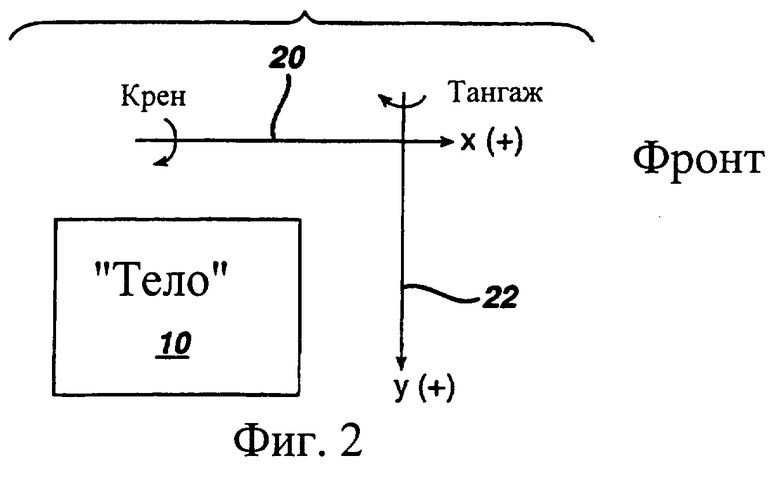
фиг.2 изображает вид сверху наклоняющегося тела согласно фиг.1,
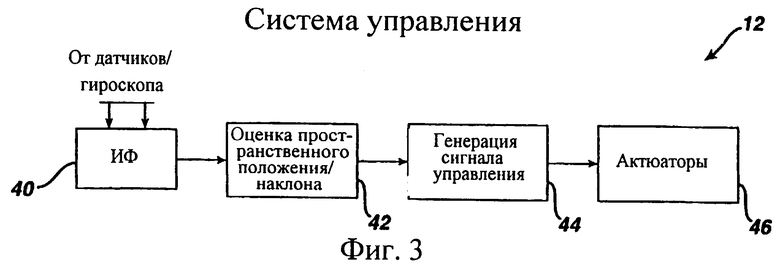
фиг.3 иллюстрирует блок-схему системы управления наклоняющегося тела согласно фиг.1,
фиг.4 изображает блок-схему устройств оценки пространственного положения и вращения, обеспеченных в соответствии с изобретением, для системы управления согласно фиг.3.
Подробное описание предпочтительных вариантов реализации изобретения
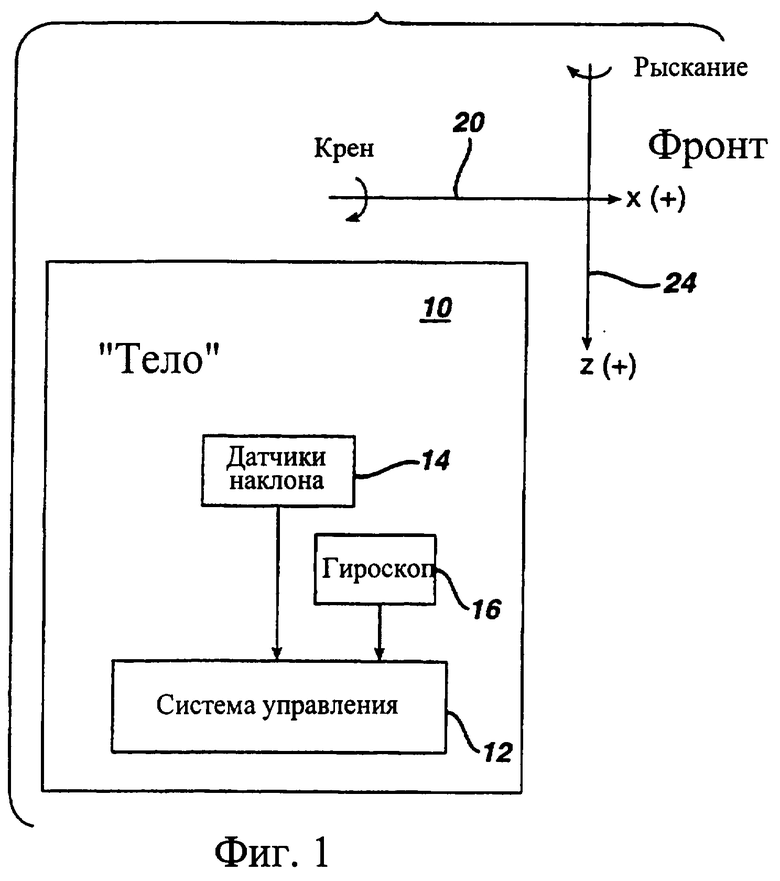
Фиг.1 представляет собой схематический обобщенный вид сбоку наклоняющегося тела 10, в отношении которого применяется настоящее изобретение.
Фиг.2 вид сверху того же самого тела 10. Тело 10 может быть произвольным объектом, для которого должно отслеживаться, представляться и/или управляться отклонение от заданного состояния. Например, тело 10 может быть роботом, управляемым двигателем наклоняемым инвалидным креслом, удаленной от берега буровой платформой, надводным кораблем, или лодкой, или подводным морским судном, наклоняющимся железнодорожным локомотивом или автомобилем, заполненной пассажирами замкнутой оболочкой или транспортным средством в развлекательной поездке, устройством моделирования полета, или хранилищем, используемым для того, чтобы содержать и избирательно вливать материал, используемый в химической реакции или в другом производственном процессе. Тело 10 также может быть автомобилем. Система управления 12, соединенная с телом 10, принимает входные сигналы из одного или более устройств 14, воспринимающих наклон, и из одного или более устройств 16 восприятия угловой скорости. Устройства 14, воспринимающие наклон, могут быть обычными жидкостными датчиками наклона и/или акселерометрами. Предполагается, что имеется один или более датчиков наклона. Датчик 16 угловой скорости может быть представленным обычным гироскопом или другим известным устройством восприятия угловой скорости. Предполагается, что имеется один или большее количество датчиков угловой скорости.
Система координат для последующего обсуждения может быть установлена так, как иллюстрируется на фиг.1 и 2. Горизонтальное направление вперед рассматривается как положительное направление оси х, которое обозначено стрелкой 20. Положительное направление оси у рассматривается в горизонтальном направлении, указывающем направо и перпендикулярном к оси х, как обозначено стрелкой 22 (фиг.2). Положительное направление оси z рассматривается как указанное вертикально прямо вниз, как обозначено стрелкой 24 (фиг.1). Наклон будет определяться как угловое отклонение от вертикальной линии, имеющее диапазон, ограниченный от плюс до минус 180° . Направление наклона определяется в терминах осей х и у. Вращение вокруг оси х будет рассматриваться как крен, причем положительный крен является отклонением вправо. Тангаж определяется как вращение вокруг оси у, при этом положительный тангаж является наклоном назад. Рыскание определяется как вращение вокруг (вертикальной) оси z, при этом положительное рыскание определяется как вращение направо. Следует отметить, что данные определения подчиняются правилу правой руки. Вышеупомянутые определения углов тангажа и крена являются аналогичными для эйлеровых углов тангажа и крена, за исключением того, что эйлеровы углы применяются в специфическом порядке и создают промежуточные системы координат. В наклоняющейся системе координат, обсуждаемой здесь, принимается, что вращение вокруг вертикальной оси не существует или может игнорироваться. Для примера, курс тела 10 может быть фиксированным или не относящимся к отслеживанию и управлению наклоном или подчиняется управлению оператором - человеком, или управляется системой, которая не учитывает или не должна учитывать информацию наклона.
Фиг.3 иллюстрирует блок-схему компонентов системы 12 управления, показанной на фиг.1. Система 12 управления включает интерфейс 40, через который система 12 управления принимает сигналы, выводимые из датчиков 14 наклона и гироскопа 16. Указанные сигналы обрабатываются блоком 42 оценки пространственного положения/вращения в соответствии с изобретением. На основе сигналов, выведенных из гироскопа и датчиков, блок 42 обеспечивает оценку пространственного положения и/или угловых скоростей вращения тела 10 способом, который будет описан ниже. На основе пространственного положения и/или информации вращения, обеспеченной блоком 42, блок 44 генерирует сигналы управления, для управления актюаторами 46, для управления пространственным положением тела 10. Актюаторы могут включать двигатели, соленоиды, заполняемые камеры или другие известные механические, электромеханические, гидравлические или пневматические устройства, используемые для управления пространственным положением тел различных типов, упомянутых выше. Электронные аппаратные средства, предназначенные для выполнения функций, по меньшей мере, части блоков 42 и 44, могут быть представлены одним или более обычными микропроцессорами. Кроме того, блок 44 генерации сигналов управления также предпочтительно включает схему возбуждения для обеспечения соответствующих сигналов возбуждения актюаторам 46.
Хотя система 12 управления показана на фиг.1, как находящаяся на теле 10, должно быть понятно, что, по меньшей мере, некоторые части системы 12 управления могут располагаться физически отделенными от тела 10. Например, схема обработки, предназначенная для выполнения некоторых или всех функций блоков 42 и 44, может быть удаленной от тела 10 и может принимать выходные сигналы от датчиков 14 наклона и гироскопа 16 посредством телеметрии, а также может передавать сигналы управления обратно, к телу 10, посредством подходящих беспроводных каналов связи.
Оценка пространственного положения и вращения
Далее будет описано функционирование блока 42 оценки пространственного положения/вращения.
Датчики наклона, такие, как общеизвестные жидкостные датчики, могут быть относительно свободными от дрейфа и, следовательно, обеспечивать достоверную индикацию гравитационного вектора. Таким образом, пространственное положение статической системы может быть определено относительно гравитации с использованием данных датчиков. Однако в динамических системах датчики такого типа являются чувствительными к угловому и колебательному ускорениям, и, следовательно, их сигналы должны быть отфильтрованы фильтром нижних частот для уменьшения влияния ускорений, отличных от ускорения силы тяжести. Результирующие данные обеспечивают усредненное направление силы тяжести по конечному периоду времени, заданному шириной полосы фильтра. Однако в системах, требующих быстрого времени отклика, одни только гравитационные датчики являются не адекватными.
С другой стороны, гироскоп или другой датчик угловой скорости может обеспечивать более широкую полосу пропускания и быстрый отклик, без неблагоприятного воздействия, вызванного ускорением. Хотя угловая скорость, детектируемая посредством таких датчиков, непосредственно не указывает пространственное положение системы, данные скорости могут быть проинтегрированы для формирования информации положения. Однако датчики скорости подвержены дрейфу, который может вызвать существенные погрешности при интегрировании. Процесс оценки, обеспеченный блоком 42, объединяет информацию, полученную в широкой полосе частот и в узкой полосе частот, обеспеченную соответственно гироскопом 16 и датчиками 14 наклона, для обеспечения точных данных положения и вращения, используя топологию средства оценки на основе модели.
В средстве оценки на основе модели оценка истинного положения осуществляется посредством сравнения данных датчика с внутренней моделью динамики системы. Для обеспечения непрерывного уточнения оценки используется погрешность между измеренными данными и прогнозированными данными. Степень, до которой такая погрешность воздействует на оценку, определяется весовой матрицей, Н, которая подает соответствующие погрешности состояния обратно в средство оценки. Уравнения переменных состояния для такого средства оценки приведены ниже:
dXe/dt=АХе+bu+Н(y-yе);
yе=Схе+du;
dx/dt=Ax+Вu;
y=Сх+Du,
где х - вектор состояния системы;
xе - оцененный вектор состояния;
y - выходной вектор системы;
yе - оцененный выходной вектор;
u - входной вектор системы/ средства оценки;
А - системная матрица;
В - входная матрица;
С - выходная матрица;
D - матрица входных/выходных параметров;
Н - матрица обратной связи.
Заметим, что нижний индекс "е" обозначает оцененные параметры. Внутренняя модель системы определена матрицей (А, В, С, D). Матрица Н обратной связи определяет устойчивость оценки. Устойчивая формула оценки через какое-то время достигнет равновесия, в котором и фактическое, и оцененное состояния равны (xе=х). Внутренняя модель часто основана на простых интеграторах. Эффективность такой простой модели связана с тем фактом, что интегрирование и дифференцирование являются фундаментальными для физических явлений. Например, скорость - это производная от положения: v=dx/dt. Следовательно, задавая простой интегратор первого порядка с параметрами А=0, В=1, С=1, D=0 и коэффициент обратной связи Н=k1, можно создать средство оценки, которое комбинирует измеренное статическое положение системы, θ о, и измеренное динамическое положение, θ , так, что оценка, θ е, является точной в полном частотном диапазоне. В действительности же оценка является частотно-зависимой взвешенной суммой, взятой из двух измерений. Ниже приведено преобразование Лапласа для указанного результата:
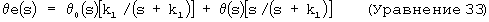
Заметим, что на низкой частоте (s=0), оцененное положение приближается к измерению положения с низкой полосой пропускания, θ o, а на высокой частоте оцененное положение приближается к измерению положения с широкой полосой пропускания, θ . Таким образом, данные для широкой и узкой ширины полосы объединяются.
Более полезная оценка может быть получена, если средство оценки основано на простом интеграторе второго порядка. В этом случае для осуществления обратной связи с измерениями θ о, выполняемыми в узкой полосе частот, может использоваться матрица обратной связи в виде Н=[k1, k2]T посредством выходной матрицы С=[1, 0]. Преобразование Лапласа результирующего положения и оценок скорости приведены ниже:
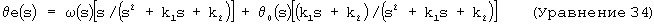
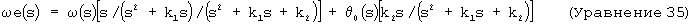
где ω (s) - измеренное значение dθ /dt в s - области.
Следовательно, такая топология средства оценки объединяет положение, измеренное с узкой полосой спектра, θ о, со скоростью ω , измеренной в широкой полосе. На низких частотах оцененное положение приближается к положению θ о, измеренному с узкой полосой спектра, как и прежде. На высокой частоте оцененное положение приближается к интегралу измерений скорости ω , измеренных в широкой полосе, что эквивалентно положению θ , измеренному с широкой полосой пропускания. Аналогичный результат получается для оцененной скорости. Таким образом, данный тип средства оценки хорошо подходит для создания оценки углового положения и скорости из данных наклона, полученных с узкой полосой, и данных скорости, полученных с широкой полосой. Коэффициенты передачи k1 и k2 выбираются таким образом, чтобы была получена соответствующая ширина полосы пропускания фильтра и стабильность. Заметим, что подстановка k2=0 и ω (s)=sθ (s) в уравнение 34 производит ту же самую оценку положения первого порядка, которая приведена в уравнении 33.
Известно, что кватернионы могут использоваться для отслеживания пространственного положения системы при произвольном угловом движении. Кроме того, кватернионы представляют собой эффективную в вычислительном отношении систему обозначений, а также свободны от сингулярностей, с которыми сталкиваются углы Эйлера. Также известно, что данные от широкополосных и узкополосных датчиков могут быть объединены, используя средства оценки для обеспечения точных данных в пределах всей полосы пропускания. Однако кватернионы не поддаются прямым физическим измерениям, и это усложняет вывод абсолютной кватернионной опорной координаты из данных датчика наклона. Без такой опорной координаты для средства оценки становится невозможным предотвратить дрейф гироскопа от искажения проинтегрированного кватерниона и, в конечном счете, приводит к потере отслеживания системой ее углового положения.
Из предыдущего обсуждения напомним, что обычные кватернионы для однозначного представления вращения требуют двух вращающихся векторов и двух внешних опорных координат. Однако с одними датчиками наклона только одна опорная координата, направленная к центру земли, является доступной. Настоящее изобретение решает данную задачу для систем, связанных с наклоном, посредством обеспечения модифицированной кватернионной системы обозначений, в которой только три элемента из четырех обычных элементов являются ненулевыми, и необходима только одна опорная координата для того, чтобы однозначным образом представить пространственное положение (наклон) в кватернионной форме. Данное решение предполагает, что системе не требуется знание о ее курсе, и, следовательно, нет необходимости отслеживать изменения угла рыскания (вращение относительно вертикальной оси).
Основываясь на предыдущем рассмотрении, вычисление кватернионных коэффициентов от единственной опорной точки требует, чтобы опорный вектор в каждой системе был перпендикулярен оси вращения. Для наклоняющихся систем, с направлением силы тяжести в качестве опорного, это эквивалентно требованию, чтобы ось вращения всегда оставалась горизонтальной. Если ось вращения, n, всегда является горизонтальной, то z-компонента оси должна быть тождественно равна нулю. Обращаясь к определению кватернионных единичных компонент, это обстоятельство подразумевает, что q3-компонента кватерниона также должна быть тождественно равна нулю. Следовательно, условие q3=0 становится ограничением. Таким образом, результирующий кватернион был модифицирован и содержит только три значащих компоненты.
Ограничение q3=0 также должно быть удовлетворено, в то время как уравнение для скорости кватерниона (уравнение 28 или 29) интегрируется. Данное условие может сохраняться в процессе интегрирования до тех пор, пока также сохраняется условие dq3/dt=0. Из уравнений 28 и 29 следует, что должно выполняться одно из следующих условий:
0=dq3/dt=-q2ω 1+q1ω 2+q0ω 3 (для интегрирования в системе координат тела) (уравнение 36)
0=dq3/dt=-q2ω E1+q1ω E2+q0ω E3 (для интегрирования в системе координат земли) (уравнение 37)
Для того чтобы удовлетворить одному из этих ограничений, по меньшей мере, одному параметру нужно позволить изменяться произвольным образом, как требуется. В системе координат тела три компоненты угловых скоростей и три модифицированных кватернионных компоненты - все содержат необходимую информацию. Однако в земной системе координат предполагалось, что компонента рыскания угловой скорости не важна, потому что система основана на исследовании наклона. Следовательно, истинная компонента рыскания может быть заменена виртуальной компонентой рыскания, которая удовлетворяет вышеупомянутому ограничению. Практически это может быть выполнено посредством преобразования измеренных угловых скоростей в системе координат тела к земной системе координат. Результирующий угол рыскания в земной системе координат, затем может быть заменен виртуальным углом рыскания в земной системе координат, который удовлетворяет следующему уравнению ограничения:
ω 'E3=(q1ω E2-q2ω E1)/q0 (виртуальный угол рыскания в земной системе координат, удовлетворяющий условию: dq3/dt=0) (уравнение 38)
Данная компонента угла рыскания в земной системе координат может быть подставлена обратно в первоначальное кватернионное уравнение скорости (уравнение 29) для устранения явной зависимости от угла рыскания. Для того чтобы отличать модифицированный кватернион с тремя элементами от других кватернионов, модифицированный кватернион будет теперь обозначен символом "е", а не "q". Компоненты могут тогда быть записаны:
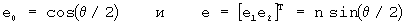
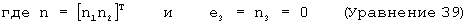
После исключения ω E3 и e3 модифицированное кватернионное уравнение для скорости принимает вид:
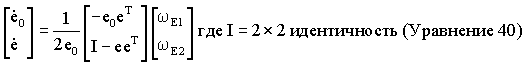
Матрица вращении REB (уравнение 32) также может быть упрощена путем исключения ω E3 и е3 следующим образом:
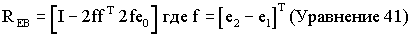
Объединяя эти результаты и учитывая, что ω е=RЕВω, модифицированная кватернионная скорость по отношению к земной системе координат может быть записана как функция угловой скорости в системе координат, связанной с телом, следующим образом:
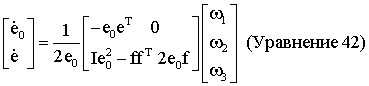
Данное выражение может быть записано более кратко в матричной форме следующим образом:

Используя указанный результат, модифицированные кватернионные скорости могут быть проинтегрированы, чтобы получить модифицированный кватернион. Однако в данном уравнении вектор угловой скорости, ω , предполагается идеальным и не обеспечивается никакой компенсации дрейфа в фактических данных угловой скорости из гироскопа. Вообще говоря, для осуществления коррекции дрейфа смещение должно быть вычтено из исходных данных гироскопа. Затем скорректированная угловая скорость в виде ω '=ω -ω drift используется в вышеупомянутом уравнении вместо параметра ω . Ситуация дополнительно усложняется тем, что дрейф гироскопа является функцией времени. Следовательно, член коррекции дрейфа должен непрерывно обновляться. Поэтому требуется использование топологии средства оценки второго порядка, описанной ранее.
Задача средства оценки заключается в сравнении кватерниона, полученного интегрированием кватернионной скорости, с кватернионом, полученным из данных наклона. Полагая, что какая-либо установившаяся ошибка обусловлена только дрейфом гироскопа, величина такой погрешности может использоваться для регулировки члена коррекции дрейфа гироскопа. Коэффициенты передачи средства оценки выбираются так, что установившаяся ошибка через какое-то время сводится к нулю. Выбор значений коэффициентов передачи лежит в пределах возможностей специалистов, и, следовательно, нет необходимости в его дальнейшем обсуждении.
Для отрегулирования члена коррекции кватернионная погрешность должна быть преобразована обратно в погрешность угловой скорости. Это осуществляется, используя первоначальное кватернионное уравнение скорости, которое было решено для угловой скорости в земной системе координат, как было показано:
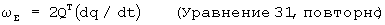
Интегрирование этого выражения по времени дает следующий результат:
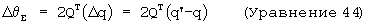
Следовательно, вышеупомянутое уравнение может использоваться для преобразования погрешности между оцененным кватернионом и кватернионом наклона (δ q=q'-q) в погрешность угла наклона, Δ θ E. Напомним, что в данном случае мы используем модифицированный кватернион, для которого q3=0 как для q, так и для Q. Однако компонента рыскания в земной системе координат, полученная таким образом, не имеет силы, поскольку кватернион был произведен, используя виртуальный угол рыскания в земной системе координат. Для получения правильной угловой погрешности вместо компоненты погрешности Δ θ E3 должен быть подставлен исходный угол рыскания в земной системе. Выражение для угла рыскания в земной системе координат может быть получено из ω е=RЕВω, где q3=0, и приведено ниже:
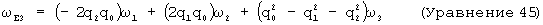
После подстановки результирующий вектор угловой погрешности в земной системе определяется выражением: Δ θ E'=[Δ θ E1, Δ θ E2, Δ θ E3]T. Так как гироскоп находится в системе координат тела, угловая погрешность в земной системе координат должна быть преобразована в систему, связанную с телом, используя выражение: Δ θ E3=REBΔθ E'. Затем результирующая угловая погрешность может использоваться средством оценки для формирования члена коррекции дрейфа гироскопа.
Далее рассмотрим способ, посредством которого данные наклона преобразуются в модифицированный кватернион. Ранее было показано, что кватернионные компоненты могут быть получены посредством формирования скалярного и векторного произведения двух единичных векторов, перпендикулярных к оси вращения и разнесенных на угол θ /2. Два таких вектора могут быть построены, используя внешнюю опорную точку в центре земли (то есть направление силы тяжести, которое измерено датчиком наклона). Пусть исходный вектор силы тяжести будет обозначен как Gi и конечный вектор силы тяжести будет обозначен символом Gf. (Данные, соответствующие исходному вектору силы тяжести Gi, могут быть получены во время процедуры инициализации и могут быть сохранены для дальнейшего использования. "Конечный" вектор силы тяжести Gf должен быть обновлен в процессе действия средства оценки.)
Пусть эти два вектора пронормированы следующим образом:
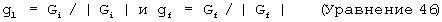
При использовании указанных нормализованных векторов силы тяжести требуемые единичные векторы могут быть построены следующим образом:
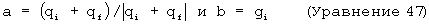
Наконец, кватернионные компоненты могут быть получены, вычисляя скалярные и векторные произведения, как показано ниже:
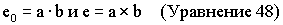
Согласно построению векторное произведение а и b формирует вектор, который является перпендикулярным к вектору силы тяжести в каждой системе. Следовательно, этот вектор также должен быть горизонтальным. Тем самым подразумевается, что z-компонента кватерниона - тождественно нулевая, как требуется. Таким образом, только три первых элемента кватерниона нетривиальны и удовлетворяют форме модифицированного кватерниона.
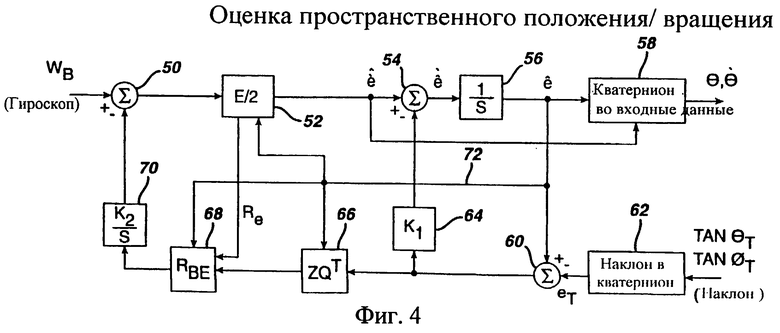
Полный процесс оценки, описанный выше, иллюстрируется на блок-схеме, изображенной на фиг.4.
Топология средства оценки разделяется на два контура: контур k1 и контур k2. Контур k1 обеспечивает узкополосную фильтрацию данных от датчика наклона и определяет величину погрешности, которая используется для регулирования оцененной кватернионной скорости. Контур k2 обеспечивает коррекцию дрейфа для данных гироскопа. Поскольку гироскоп находится в системе координат тела, контур k2 должен находиться на стороне тела преобразования координат. Коэффициент передачи k2 определяет величину погрешности, которая используется для корректировки дрейфа в данных гироскопа. Затем взвешенная погрешность интегрируется так, чтобы контур через какое-то время достиг нулевой установившейся ошибки. Другими словами, когда кватернионная погрешность достигает нуля, выходной сигнал из k2 интегратора прекращает изменяться и член коррекции дрейфа остается постоянным.
На фиг.4 блок 50 суммирования в контуре k2 прикладывает взвешенный сигнал погрешности (который может также рассматриваться как сигнал коррекции дрейфа) к информации угловой скорости, выведенной из гироскопа 16, чтобы произвести скорректированную информацию угловой скорости. Скорректированная информация угловой скорости преобразуется в земную систему координат и преобразуется в модифицированный кватернион в блоке 52. Как обозначено меткой Е/2 в блоке 52, вычисления, выполняемые в данном блоке, производятся в соответствии с уравнениями 43 и 42, которые обсуждались выше. Результирующая информация оцененной скорости, которая представлена в вышеописанной модифицированной кватернионной форме, подается в качестве входного сигнала в блок 54 суммирования. В блоке 54 коррекция, обеспеченная контуром k1, применяется к кватернионной информации оцененной скорости для формирования данных, указывающих на изменения в оцененном положении. Эти данные (которые могут быть упомянуты нами как сигнал оцененной разности положения), в свою очередь, интегрируются в блоке 56 для обеспечения модифицированных кватернионных данных оцененного положения. В блоке 58 модифицированные кватернионные данные оцененного положения, выведенные из блока 56, а также модифицированная кватернионная информация оцененной скорости, выведенная из блока 52, преобразуются в углы Эйлера для выведения их в блок 44 формирования сигнала управления (фиг.3). Такое преобразование легко осуществляется при использовании следующих уравнений. (Хотя эти уравнения используют тригонометрические функции, сложность вычислений является минимальной, и вычисления могут быть легко выполнены, используя справочные таблицы.)
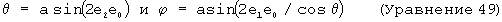
Данные уравнения также можно упростить, используя аппроксимации для малых углов, в случае, когда область движения наклоняющейся системы является ограниченной.
Если генератор 44 управляющих сигналов такого типа, который обеспечивает выходные кватернионные сигналы, а не эйлеровы сигналы, то блок 58 может быть опущен, и кватернионная информация оцененного положения и скорости (в модифицированной форме, обеспеченной в соответствии с изобретением) может подаваться непосредственно в генератор управляющего сигнала.
В любом случае информация оцененного положения в модифицированной кватернионной форме подается в качестве входного сигнала в блок 60 суммирования, в котором она сравнивается с текущей информацией наклона, выведенной из датчиков 14 наклона, как преобразованной в модифицированную кватернионную форму в блоке 62. (Сигнал, сформированный в блоке 62, может быть упомянут нами как модифицированный кватернионный опорный сигнал положения.) Преобразование, выполняемое в блоке 62, осуществляется в соответствии с процедурой, описанной выше, в связи с уравнениями 46-48. Результирующий сигнал погрешности, выведенный из блока 60 суммирования, взвешивается на коэффициент передачи k1 в блоке 64 и затем подается в качестве вышеупомянутого корректирующего сигнала в блок 54. Выходной сигнал из блока 60 (который может рассматриваться как сигнал погрешности положения) также подается в качестве входного сигнала в блок 66. В соответствии с уравнением 44 блок 66 преобразует погрешность между оцененным кватернионом и кватернионом наклона в погрешность угла наклона. Непродуктивная компонента рыскания результирующего выхода сигнала из блока 66 заменяется компонентой рыскания в земной системе координат, которая является доступной из результатов обработки блока 52, и результирующий вектор погрешности угла преобразуется в систему координат тела в блоке 68. Затем выходной сигнал из блока 68 интегрируется и взвешивается на коэффициент передачи k2 в блоке 70, и результирующий сигнал подается в блок 50 суммирования в качестве вышеупомянутого сигнала коррекции дрейфа.
Следует отметить, что коэффициенты, требуемые для процессов в блоках 52, 66 и 68, берутся из модифицированной кватернионной информации, выведенной из блока 56 интегрирования, как показано поз. 72 на фиг.4.
Как будет понятно специалистам, процессы, иллюстрируемые в виде блок-схемы фиг.4, предпочтительно могут быть выполнены одним или более соответственно запрограммированными вычислительными устройствами (например, одним или более микропроцессорами), которые составляют часть системы 12 управления.
В устройстве оценки пространственного положения и вращения, обеспеченном в соответствии с изобретением, информация в широкой полосе частот, обеспеченная датчиками вращения, и информация в узкой полосе частот от датчиков наклона объединяются в новейшей модифицированной кватернионной системе обозначений, имеющей три элемента вместо обычных четырех элементов. Результирующий оцененный кватернион имеет силу в пределах заданной ширины полосы частот и не дрейфует со временем. Вычисления, которые должны будут осуществлены, могут быть эффективно обработаны, используя простую арифметику, такую, как умножение, сложение и извлечение квадратного корня. Модифицированное кватернионное средство оценки применимо к широкому диапазону систем, в которых должен отслеживаться и/или управляться наклон.
Вышеупомянутое описание изобретения предназначено для иллюстративных целей, а не для ограничения. Специалист может предложить различные изменения или модификации описанных вариантов воплощения, которые не выходят за рамки и не отклоняются от сущности настоящего изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ управления космическим аппаратом дистанционного зондирования Земли | 2019 |
|
RU2722598C1 |
| Способ калибровки погрешностей электростатических гироскопов бескарданной инерциальной системы ориентации в условиях орбитального космического аппарата | 2018 |
|
RU2678959C1 |
| Способ определения параметров ориентации объекта при помощи полуаналитической инерциальной навигационной системы с географической ориентацией осей четырехосной гироплатформы | 2022 |
|
RU2782334C1 |
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2635820C1 |
| Бесплатформенная инерциальная курсовертикаль | 2016 |
|
RU2643201C2 |
| Малогабаритный навигационный комплекс | 2016 |
|
RU2644632C1 |
| РЕЗЕРВНАЯ СИСТЕМА ДЛЯ ИНДИКАЦИИ КУРСА И ПРОСТРАНСТВЕННОГО ПОЛОЖЕНИЯ НА САМОЛЕТЕ | 2000 |
|
RU2236697C2 |
| Способ коррекции углов ориентации ЛА по сигналам от одноантенной СНС | 2022 |
|
RU2790081C1 |
| Способ автономной ориентации объектов в околоземном пространстве | 2022 |
|
RU2787971C1 |
| Способ определения углов ориентации ЛА на вертикальных траекториях полета | 2017 |
|
RU2671291C1 |
Изобретение относится к отслеживанию и управлению наклоняющимися телами. На основе сигналов, выводимых из гироскопа и датчиков наклона, осуществляется отслеживание и управление пространственным положением наклоняющегося тела. Сигнал, выводимый из гироскопа, преобразуется и интегрируется для формирования информации оцененного положения в форме модифицированного кватерниона, в которой компонента рыскания ограничена нулевым значением. Модифицированная кватернионная информация в аналогичной форме также формируется из сигналов, выводимых из датчика наклона, и используется для определения и корректировки компоненты погрешности в информации оцененного положения. Дрейф гироскопа также корректируется на основе выходного сигнала датчика наклона. Техническим результатом является повышение надежности отслеживания ориентации объекта в более широкой полосе частот, а также упрощение вычислительного процесса. 4 с.. и 7 з.п. ф-лы, 4 ил.
выведение информации угловой скорости из упомянутого устройства, воспринимающего угловую скорость;
преобразование и интегрирование упомянутой выведенной информации угловой скорости для формирования первой кватернионной информации положения так, чтобы упомянутая первая кватернионная информация положения была ограничена таким образом, чтобы представлять вращение относительно горизонтальной оси в системе координат, связанной с землей;
выведение информации наклона из указанного устройства, воспринимающего наклон;
обработка упомянутой выведенной информации наклона для формирования второй кватернионной информации положения так, чтобы вторая кватернионная информация положения была ограничена таким образом, чтобы представлять вращение относительно горизонтальной оси в системе координат, связанной с землей;
сравнение упомянутой первой кватернионной информации положения с упомянутой второй кватернионной информацией положения для формирования информации о погрешности и
использование упомянутой информации о погрешности для компенсирования дрейфа в упомянутом устройстве восприятия угловой скорости.
выведение информации угловой скорости из упомянутого устройства, воспринимающего угловую скорость;
формирование модифицированной кватернионной информации об угловой скорости из упомянутой выведенной информации угловой скорости, причем упомянутая модифицированная кватернионная информация скорости представляется в форме скалярной величины и двухкомпонентного вектора;
интегрирование упомянутой модифицированной кватернионной информации об угловой скорости для формирования первой модифицированной кватернионной информации пространственного положения, причем упомянутый этап формирования модифицированной кватернионной информации скорости ограничивается так, чтобы первая модифицированная кватернионная информация пространственного положения была представлена в форме:
е=e0+e1i+e2j, где i, j - единичные мнимые векторы, которые удовлетворяют следующим соотношениям друг с другом и с третьим мнимым единичным вектором k:
i2=j2=k2=ijk=-1, ij=-ji=k, jk=-kj=i, ki=-ik=j;
выведение информации наклона из устройства, воспринимающего наклон;
формирование второй модифицированной кватернионной информации положения из упомянутой выведенной информации наклона, причем упомянутая вторая модифицированная кватернионная информация положения представляется в упомянутой форме:
e=e0+e1i+e2j;
сравнение упомянутой первой модифицированной кватернионной информации положения с упомянутой второй модифицированной кватернионной информацией положения для формирования модифицированной кватернионной информации погрешности положения;
преобразование упомянутой модифицированной кватернионной информации погрешности положения в сигнал ошибки угловой скорости; и
использование упомянутого сигнала ошибки угловой скорости для компенсации погрешности в упомянутой выведенной информации угловой скорости.
упомянутая информация угловой скорости обеспечивается в первой системе координат, а упомянутая информация наклона генерируется во второй системе координат, отличной от упомянутой первой системы координат;
упомянутый этап формирования упомянутой модифицированной кватернионной информации включает преобразование упомянутой выведенной информации угловой скорости из упомянутой первой системы координат в упомянутую вторую систему координат; и
дополнительно содержит этап преобразования упомянутого сигнала ошибки угловой скорости и упомянутой второй системы координат в упомянутую первую систему координат до использования упомянутого этапа.
формирование информации угловой скорости в системе координат тела;
приложение сигнала коррекции дрейфа к упомянутой информации угловой скорости для формирования скорректированной информации угловой скорости;
обработка упомянутой скорректированной информации угловой скорости с использованием модифицированной кватернионной информации оцененного положения, чтобы формировать модифицированную кватернионную информацию оцененной скорости, отнесенную к земной системе координат, причем упомянутая модифицированная кватернионная информация оцененной скорости состоит из скалярной компоненты и двух векторных компонент;
регулировка упомянутой модифицированной кватернионной информации оцененной скорости на основе взвешенного сигнала коррекции положения для формирования сигнала оцененной разности положения;
интегрирование упомянутого сигнала оцененной разности положения для формирования упомянутой модифицированной кватернионной информации оцененного положения, причем упомянутая модифицированная кватернионная информация оцененного положения состоит из скалярной компоненты и двух векторных компонент;
формирование информации наклона в упомянутой земной системе координат;
использование упомянутой информации наклона для формирования модифицированной кватернионной информации опорного положения, причем упомянутая модифицированная кватернионная информация опорного положения состоит из скалярной компоненты и двух векторных компонент;
вычитание упомянутой модифицированной кватернионной информации опорного положения из упомянутой модифицированной кватернионной информации оцененного положения для формирования сигнала ошибочного положения;
взвешивание упомянутого сигнала ошибочного положения для формирования упомянутого взвешенного сигнала погрешности положения;
преобразование упомянутого сигнала ошибочного положения в сигнал погрешности угла наклона, используя упомянутую модифицированную кватернионную информацию оцененного положения;
формирование вектора погрешности угла из компонент тангажа и крена упомянутого сигнала угла наклона, и из компоненты рыскания сигнала угловой скорости, сформированного посредством преобразования упомянутой скорректированной информации угловой скорости в упомянутую земную систему координат, используя упомянутую модифицированную кватернионную информацию оцененного положения;
преобразование упомянутого вектора погрешности угла из упомянутой земной системы координат в упомянутую систему координат тела, используя упомянутую модифицированную кватернионную информацию оцененного положения, и
применение взвешенного интегрирования к упомянутому преобразованному вектору погрешности угла для формирования упомянутого сигнала коррекции дрейфа.
преобразование упомянутой модифицированной кватернионной информации оцененной скорости и упомянутой модифицированной кватернионной информации оцененного положения для формирования выходной информации углов Эйлера и
выведение упомянутой выходной информации углов Эйлера в устройство формирования управляющего сигнала.
устройство, воспринимающее наклон, установленное на упомянутом теле для выведения информации наклона;
устройство, воспринимающее угловую скорость, установленное на упомянутом теле для выведения информации угловой скорости;
устройство формирования модифицированной кватернионной информации скорости из упомянутой информации угловой скорости, выводимой из упомянутого устройства, воспринимающего угловую скорость, причем упомянутая модифицированная кватернионная информация скорости представляется в форме скалярной величины и двухкомпонентного вектора;
блок интегрирования упомянутой модифицированной кватернионной информации скорости для формирования первой модифицированной кватернионной информации пространственного положения, причем упомянутая первая модифицированная кватернионная информация пространственного положения представляется в форме е=e0+e1i+e2j, где i, j - единичные мнимые векторы, которые удовлетворяют следующим соотношениям друг с другом и с третьим мнимым единичным вектором k:
i2=j2=k2=ijk=-1, ij=-ji=k, jk=-kj=i, ki=-ik=j;
блок формирования второй модифицированной кватернионной информации положения из упомянутой информации наклона, выводимой из упомянутого устройства, воспринимающего наклон, причем упомянутая вторая модифицированная кватернионная информация положения представляется в упомянутой форме:
e=e0+e1i+e2j;
блок сравнения упомянутой первой модифицированной кватернионной информации положения с упомянутой второй модифицированной кватернионной информацией положения для формирования модифицированной кватернионной информации погрешности положения;
блок преобразования упомянутой модифицированной кватернионной информации погрешности положения в сигнал ошибки угловой скорости; и
блок компенсации погрешности в упомянутой информации угловой скорости, выводимой из упомянутого устройства, воспринимающего угловую скорость, на основе упомянутого сигнала ошибки угловой скорости.
| US 5875993 А, 02.03.1999 | |||
| Устройство для упругого шлифования | 1981 |
|
SU963817A1 |
| US 4742356 A, 03.05.1988 | |||
| СПОСОБ УПРАВЛЕНИЯ РАЗВОРОТОМ КОСМИЧЕСКОГО АППАРАТА | 1994 |
|
RU2093433C1 |
| СПОСОБ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ПО МЕСТНОЙ ВЕРТИКАЛИ ПЛАНЕТЫ | 1991 |
|
RU2021174C1 |
Авторы
Даты
2005-05-27—Публикация
2001-02-01—Подача