ОБЛАСТЬ ТЕХНИКИ
Изобретение относится к области квантовых технологий, в частности к способу получения управляющих параметров для квантовых вычислительных систем на основе ионов в ловушке, которые заставляют систему менять состояния, заданные собственным гамильтонианом, так, что эволюция в системе соответствует применению (последовательности) логических операций.
УРОВЕНЬ ТЕХНИКИ
Классическая проблема компиляции состоит в переводе кода, написанного на языке высокого уровня, в набор инструкций, которые должен выполнять компьютер. Точно так же квантовая компиляция переводит квантовые алгоритмы в серию операций, которые данный квантовый компьютер может выполнять изначально. Квантовые алгоритмы выражаются последовательностью логических (унитарных) вентилей, работающих с начальным квантовым состоянием, и приводят к унитарной эволюции указанного квантового состояния.
Следовательно, квантовый компьютер должен иметь возможность выполнять универсальный набор квантовых вентилей. Подобно классическому универсальному набору вентилей (например, И, ИЛИ и НЕ), эти универсальные наборы квантовых вентилей способны подготовить произвольную унитарную эволюцию с учетом достаточно длинной последовательности.
В уровне техники квантовая компиляция на квантовых компьютерах на основе ионов основана на компиляции каждого отдельного квантового элемента в алгоритме с использованием эвристики [1].
Заявляемый подход отличается тем, что компиляция выполняется с помощью классического (цифрового) компьютера. Техническая задача состоит в том, чтобы с помощью классического компьютера получить управляющие параметры для квантовой вычислительной системы на основе ионов в ловушке, которые заставляют квантовую систему менять состояния, заданные собственным гамильтонианом, так, что эволюция в квантовой системе соответствует применению (последовательности) логических операций.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Технический результат заключается в обеспечении получения с помощью цифрового вычислительного устройства управляющих параметры для квантовой вычислительной системы на основе ионов в ловушке, которые заставляют квантовую систему менять состояния, заданные собственным гамильтонианом, так, что эволюция в квантовой системе соответствует применению (последовательности) логических операций.
Указанный технический результат достигается за счет того, что:
В способе получения управляющих параметров для квантовой вычислительной системы на основе ионов в ловушке:
для последовательности квантовых логических элементов с помощью цифрового вычислительного устройства, реализующего вариационный квантовый алгоритм, находят на основе параметризованного анзаца управляющие параметры, которые заставляют квантовую вычислительную систему на основе ионов в ловушке менять состояния, заданные собственным гамильтонианом, так, что эволюция в указанной квантовой системе соответствует применению указанной последовательности квантовых логических элементов, причем параметризованный анзац представляет собой последовательность гейтов, параметризованную набором управляющих параметров, где указанные гейты являются гейтами квантовой вычислительной системы на основе ионов в ловушке.
В способе гейт является поворотом в гильбертовом пространстве, и управляющий параметр является углом поворота в гильбертовом пространстве.
В способе цифровое вычислительное устройство, реализующее вариационный квантовый алгоритм, выполняет итеративное обновление углов поворота в гильбертовом пространстве параметризованного анзаца для минимизации функции стоимости
В способе параметризованный анзац имеет заданную структуру и заданную глубину.
В способе структура анзаца является структурой шахматной доски.
В способе глубина параметризованного анзаца зависит от последовательности квантовых логических элементов и структуры анзаца.
В способе найденные управляющие параметры переводят в эквивалентные физические параметры для управления физическими ионами, электромагнитно захваченными в ловушку, для выполнения квантовой эволюции, в соответствии с последовательностью квантовых логических элементов.
В способе эквивалентными физическими параметрами являются, по меньшей мере, следующие: отстройка лазера от перехода несущей, отстройка лазера от перехода боковой полосы, длительность импульса, частота Раби, контролируемая интенсивностью лазерного импульса.
В способе транслятор дополнительно использует градиентные и безградиентные оптимизаторы.
Указанный технический результат достигается также за счет того, что:
цифровое вычислительное устройство для получения управляющих параметров для квантовой вычислительной системы на основе ионов в ловушке в соответствии с вышеизложенным способом реализует вариационный квантовый алгоритм, причем с помощью указанного цифрового вычислительного устройства для последовательности квантовых логических элементов находят на основе параметризованного анзаца управляющие параметры, которые заставляют квантовую вычислительную систему на основе ионов в ловушке менять состояния, заданные собственным гамильтонианом, так, что эволюция в указанной квантовой системе соответствует применению указанной последовательности квантовых логических элементов, причем параметризованный анзац представляет собой последовательность гейтов, параметризованную набором управляющих параметров, где указанные гейты являются гейтами квантовой вычислительной системы на основе ионов в ловушке.
ОПИСАНИЕ ЧЕРТЕЖЕЙ
Реализация изобретения будет описана в дальнейшем в соответствии с прилагаемыми чертежами, которые представлены для пояснения сути изобретения и никоим образом не ограничивают область изобретения.
Заявляемое изобретение проиллюстрировано фигурами 1-2, на которых изображены:
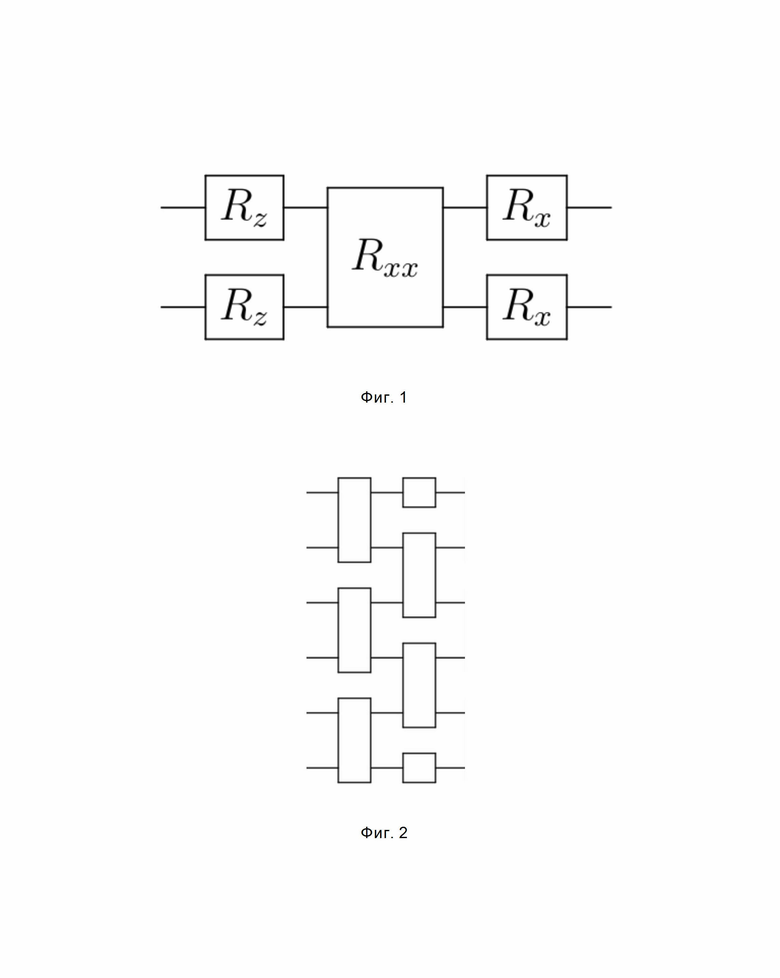
Фиг. 1 - иллюстрирует одиночный блок 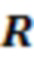 шахматного анзаца, состоящий из операций поворотов
шахматного анзаца, состоящий из операций поворотов 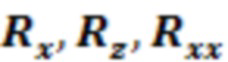 .
.
Фиг. 2 - иллюстрирует один слой шахматного анзаца, состоящий из блоков 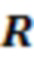 .
.
ДЕТАЛЬНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
В приведенном ниже подробном описании реализации изобретения приведены многочисленные детали реализации, призванные обеспечить отчетливое понимание настоящего изобретения. Однако, квалифицированному в предметной области специалисту будет очевидно, каким образом можно использовать настоящее изобретение, как с данными деталями реализации, так и без них. В других случаях хорошо известные методы, процедуры и компоненты не были описаны подробно, чтобы не затруднять излишне понимание особенностей настоящего изобретения.
Кроме того, из приведенного изложения будет ясно, что изобретение не ограничивается приведенной реализацией. Многочисленные возможные модификации, изменения, вариации и замены, сохраняющие суть и форму настоящего изобретения, будут очевидными для квалифицированных в предметной области специалистов.
В настоящем решении раскрыт способ управления произвольной унитарной эволюцией на ионном квантовом компьютере, описываемом последовательностью квантовых логических вентилей. Компиляция выполняется с помощью программы классического (цифрового) компьютера, реализующей вариационный квантовый алгоритм, в котором петля обратной связи минимизирует функцию стоимости на основе набора параметров, которые раскрываются в настоящем решении. Когда функция стоимости минимальна, результирующие параметры используются для управления квантовым компьютером на основе ионов для выполнения той же унитарной эволюции, что и исходный алгоритм. Следовательно, в заявленном решении также раскрыт компилятор для полного исходного квантового логического вентиля (последовательности).
Программа трансляции классического (цифрового) компьютера находит оптимальные параметры ионного квантового компьютера для составления унитарных вентилей. Впоследствии параметры могут использоваться для управления физическими ионами, электромагнитно захваченными в подходящем устройстве, для выполнения квантовой эволюции, как описано последовательностью квантовых логических вентилей.
Программа использует параметризованный анзац 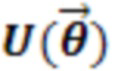 для аппроксимации исходной последовательности логических элементов
для аппроксимации исходной последовательности логических элементов  . Определения:
. Определения:
• Параметризованный анзац 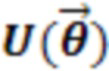 :
:
это последовательность вентилей, состоящая из поворотов в гильбертовом пространстве, параметризованная набором углов поворота 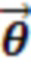 . Гейты, используемые в этой последовательности, являются родными для платформы. В установке квантовых компьютеров на основе ионов в комплект входят:
. Гейты, используемые в этой последовательности, являются родными для платформы. В установке квантовых компьютеров на основе ионов в комплект входят:
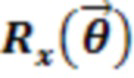 ,
, 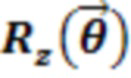 и
и 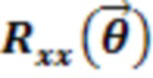 см. ссылку [2].
см. ссылку [2].
Эти гейты расположены в фиксированной структуре (также известной как слой) и повторяются фиксированное количество раз (также известной как глубина). В этом алгоритме мы используем структуру, называемую анзацем шахматной доски, изображенную на Фиг. 1 и Фиг. 2.
• Логическая (унитарная) последовательность вентилей  :
:
Это может быть любая унитарная эволюция, например, последовательность вентилей или конкретный квантовый вентиль, не входящий в собственный набор вентилей ионного квантового компьютера. Глубина (т.е. количество слоев, например, см. на Фиг. 2), необходимая для компиляции данного унитарного кода, будет зависеть от унитарного  и структуры анзаца.
и структуры анзаца.
Для параметризованного анзаца 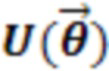 и начального логического элемента (последовательности)
и начального логического элемента (последовательности)  программа для классического компьютера реализует трансляцию путем итеративного обновления параметров (углов
программа для классического компьютера реализует трансляцию путем итеративного обновления параметров (углов 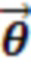 ) для минимизации реальной многозначной функции стоимости
) для минимизации реальной многозначной функции стоимости 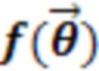 определяемое выражением (1):
определяемое выражением (1):
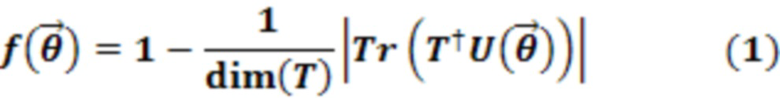
Это обозначение подразумевает вычисление абсолютного значения 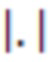 , взятого для следа матрицы
, взятого для следа матрицы 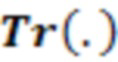 , полученного в результате умножения между матричным представлением транспонированной комплексно-сопряженной исходной логической последовательности
, полученного в результате умножения между матричным представлением транспонированной комплексно-сопряженной исходной логической последовательности 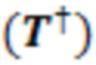 , и матричным представлением параметризованного анзаца.
, и матричным представлением параметризованного анзаца.
Если функция стоимости 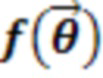 минимизируется, то
минимизируется, то 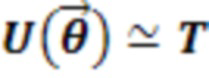 с точностью до глобальной фазы волновой функции, к которой применяется операция [3]. Глобальная фаза не поддается измерению, поэтому указанная программа выполняет перевод исходной последовательности логических элементов в исходные операции квантового компьютера на основе ионов.
с точностью до глобальной фазы волновой функции, к которой применяется операция [3]. Глобальная фаза не поддается измерению, поэтому указанная программа выполняет перевод исходной последовательности логических элементов в исходные операции квантового компьютера на основе ионов.
Это раскрытие относится к параметрам, реализованным с помощью анзаца шахматной доски, как показано на Фиг. 2. Следующие примеры случаев были проверены численно:
• 2-тоффоли гейт: [Это 3-кубитный вентиль с 2 управляющими кубитами и 1 целевым кубитом. Оператор Паули 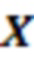 применяется к цели, если оба элемента управления находятся в состоянии
применяется к цели, если оба элемента управления находятся в состоянии 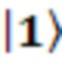 ].
].
Для составления этого гейта требуется 5 слоев анзаца в шахматном порядке.
• 3-тоффоли гейт: [Это 4-кубитный вентиль с 3 управляющими кубитами и 1 целевым кубитом. Оператор Паули 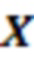 применяется к цели, если элементы управления находятся в состоянии
применяется к цели, если элементы управления находятся в состоянии 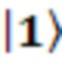 ].
].
Для составления этого гейта требуется 8 слоев анзаца в шахматном порядке.
Кроме того, было завершено исследование случайной выборки унитарных операций, которые в матричных представлениях задаются, как 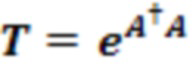 , где A - случайная (комплексная) матрица размера
, где A - случайная (комплексная) матрица размера 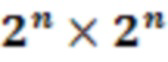 .
.
• Однородная выборка 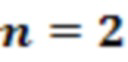 кубитных унитарных операций:
кубитных унитарных операций:
Для компиляции этих гейтов требуется в среднем 2 слоя анзаца в шахматном порядке с точностью более 1%.
• Однородная выборка 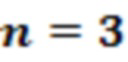 кубитных унитарных операций:
кубитных унитарных операций:
Для компиляции этих гейтов требуется в среднем 8 слоев анзаца в шахматном порядке с точностью более 1%.
• Однородная выборка 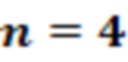 кубитных унитарных операций:
кубитных унитарных операций:
При значении функции стоимости 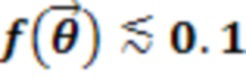 этому требованию удовлетворяют около 8 слоев шахматного анзаца.
этому требованию удовлетворяют около 8 слоев шахматного анзаца.
Программа перевода может использовать градиентные и безградиентные оптимизаторы. В случае оптимизаторов на основе градиента аналитические производные (стратегия GOAT [4]) могут быть легко рассчитаны для некоторых наиболее распространенных структур анзаца (например, анзаца в виде шахматной доски).
Физическая реализация вентилей 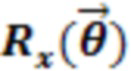 ,
, 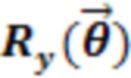 и
и 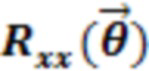 на ионном квантовом компьютере использует следующие экспериментальные параметры, которыми можно управлять напрямую:
на ионном квантовом компьютере использует следующие экспериментальные параметры, которыми можно управлять напрямую:
• 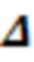 : отстройка лазера от перехода несущей;
: отстройка лазера от перехода несущей;
• 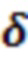 : отстройка лазера от перехода боковой полосы;
: отстройка лазера от перехода боковой полосы;
• 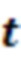 : длительность импульса.
: длительность импульса.
• 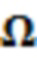 : частота Раби, контролируемая интенсивностью лазерного импульса;
: частота Раби, контролируемая интенсивностью лазерного импульса;
Другие параметры могут контролироваться программой трансляции, но обычно они фиксируются для данной экспериментальной установки:
• 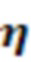 : параметр Лэмба - Дикке;
: параметр Лэмба - Дикке;
• 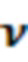 : частота электромагнитной ловушки.
: частота электромагнитной ловушки.
Мы раскрываем следующие эквивалентности, которые переводят параметры оптимизации (углы поворота 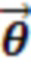 ) анзаца
) анзаца 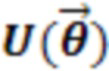 в эквивалентные экспериментальные параметры:
в эквивалентные экспериментальные параметры:
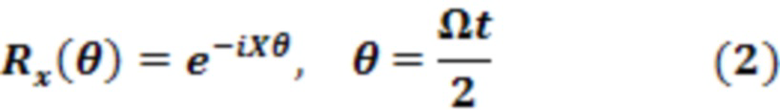
где настраиваемый параметр 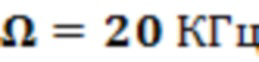 является значением по умолчанию (экспериментальным), которое мы зафиксировали в нашем численном моделировании, сделав длительность импульса
является значением по умолчанию (экспериментальным), которое мы зафиксировали в нашем численном моделировании, сделав длительность импульса 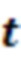 - вариационный параметр;
- вариационный параметр;
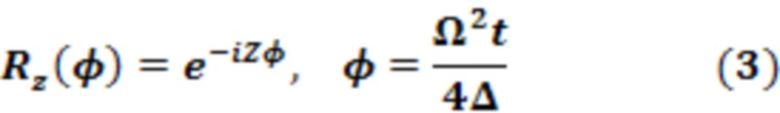
где перестраиваемый параметр 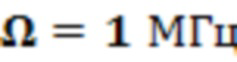 и
и 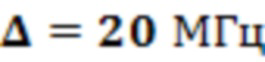 - значения по умолчанию (экспериментальные) в программе, что делает длительность импульса время
- значения по умолчанию (экспериментальные) в программе, что делает длительность импульса время 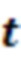 - вариационный параметр;
- вариационный параметр;
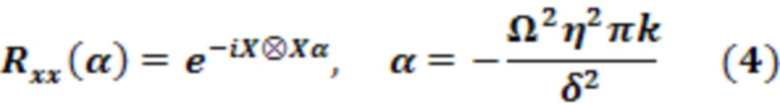
где k - целое число, параметр Лэмба-Дикке 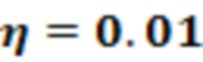 и отстройка лазера
и отстройка лазера 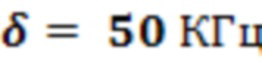 используются в нашем моделировании, что делает
используются в нашем моделировании, что делает 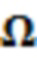 вариационным параметром.
вариационным параметром.
В другой экспериментальной установке могут использоваться другие настройки для этих физических параметров, программа перевода может приспособиться к изменению, считывая используемые значения из файла описания.
Источники
[1] С. Мартиэль, Т. Губо де Брюжьер. Метод составления квантовой схемы на квантовом процессоре с захваченными ионами. Номер публикации: 20200219002.
[2] Сирак Дж. И., Золлер П. (2000). Масштабируемый квантовый компьютер с ионами в массиве микроловушек. Nature, 404 (6778), 579-581.
[3] Хатри С., ЛаРоуз Р., Поремба А., Синчио Л., Сорнборгер А. Т. и Коулз П. Дж. (2019). Квантовая компиляция с помощью квантов. Quantum, 3, 140.
[4] Махнес С., Ассемат Э., Таннор Д. и Вильгельм Ф. К. (2018). Настраиваемая, гибкая и эффективная оптимизация управляющих импульсов для практических кубитов. Physical review letters, 120(15), 15040.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И СИСТЕМА КОМПЕНСАЦИИ ШУМОВ НА КВАНТОВОМ ПРОЦЕССОРЕ С ПОМОЩЬЮ КВАНТОВОЙ ТОМОГРАФИИ ОПЕРАЦИЙ | 2022 |
|
RU2786349C1 |
| Квантовая вычислительная система на основе фотонных чипов | 2023 |
|
RU2806840C1 |
| Система и способ решения прикладных задач материаловедения с помощью сопряжения квантовых и классических устройств | 2023 |
|
RU2814969C1 |
| Архитектура квантовых вычислительных устройств для решения прикладных задач в области материаловедения | 2023 |
|
RU2821360C1 |
| СПОСОБ ВЫПОЛНЕНИЯ КВАНТОВЫХ ВЫЧИСЛЕНИЙ С ИСПОЛЬЗОВАНИЕМ КУДИТОВ | 2020 |
|
RU2761771C1 |
| Способ формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов | 2023 |
|
RU2825968C1 |
| Устройство для реализации двухкубитного вентиля CZ между сверхпроводниковыми кубитами на основе высокой кинетической индуктивности | 2022 |
|
RU2795679C1 |
| СПОСОБ И УСТРОЙСТВО КВАНТОВОЙ ОБРАБОТКИ | 2016 |
|
RU2742504C2 |
| Квантовая вычислительная система на основе нейтральных атомов | 2023 |
|
RU2814970C1 |
| КВАНТОВАЯ СХЕМА, КВАНТОВАЯ МИКРОСХЕМА И КВАНТОВЫЙ КОМПЬЮТЕР | 2022 |
|
RU2831759C2 |
Изобретение относится к способу выполнения квантового алгоритма в виде последовательности квантовых логических вентилей с помощью квантовой системы на основе ионов в ловушке. Технический результат заключается в получении с помощью цифрового вычислительного устройства управляющих параметров для квантовой вычислительной системы на основе ионов в ловушке, которые заставляют квантовую систему менять состояния, заданные собственным гамильтонианом, так, что эволюция в квантовой системе соответствует последовательности логических операций. Способ содержит этапы, на которых с помощью вычислительного устройства, соединенного с квантовой вычислительной системой: получают исходную последовательность логических вентилей T; выполняют аппроксимацию исходной последовательности логических вентилей T; выполняют поиск оптимальных параметров в виде значений углов 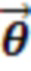 полученной последовательности логических вентилей T; выполняют перевод исходной последовательности логических элементов T в эквивалентные физические операции квантовой системы на основе ионов с помощью полученной последовательности оптимальных параметров, формируя управляющие параметры для выполнения последовательности квантового алгоритма квантовой системой, при этом упомянутые параметры включают в себя следующее: отстройка лазера от перехода несущей; отстройка лазера от перехода боковой полосы; длительность импульса; частота Раби, контролируемая интенсивностью лазерного импульса; параметр Лэмба-Дикке; частота электромагнитной ловушки; передают последовательность оптимальных параметров выполнения физических операций в квантовую систему; выполняют с помощью квантовой системы упомянутый квантовый алгоритм с помощью полученной последовательности оптимальных параметров выполнения физических операций, осуществляя управление ионами, электромагнитно захваченными в квантовой системе. 2 ил.
полученной последовательности логических вентилей T; выполняют перевод исходной последовательности логических элементов T в эквивалентные физические операции квантовой системы на основе ионов с помощью полученной последовательности оптимальных параметров, формируя управляющие параметры для выполнения последовательности квантового алгоритма квантовой системой, при этом упомянутые параметры включают в себя следующее: отстройка лазера от перехода несущей; отстройка лазера от перехода боковой полосы; длительность импульса; частота Раби, контролируемая интенсивностью лазерного импульса; параметр Лэмба-Дикке; частота электромагнитной ловушки; передают последовательность оптимальных параметров выполнения физических операций в квантовую систему; выполняют с помощью квантовой системы упомянутый квантовый алгоритм с помощью полученной последовательности оптимальных параметров выполнения физических операций, осуществляя управление ионами, электромагнитно захваченными в квантовой системе. 2 ил.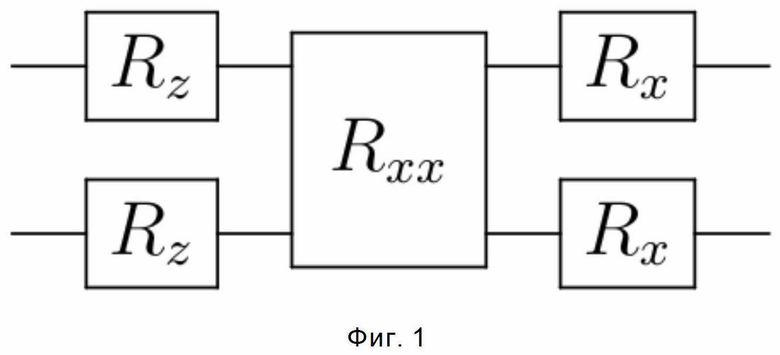
Компьютерно-реализуемый способ выполнения квантового алгоритма в виде последовательности квантовых логических вентилей с помощью квантовой системы на основе ионов, содержащий этапы, на которых:
с помощью вычислительного устройства, соединенного с квантовой вычислительной системой:
получают исходную последовательность логических вентилей T;
выполняют аппроксимацию исходной последовательности логических вентилей T;
выполняют поиск оптимальных параметров в виде значений углов 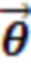 полученной последовательности логических вентилей T;
полученной последовательности логических вентилей T;
выполняют перевод исходной последовательности логических элементов T в эквивалентные физические операции квантовой системы на основе ионов с помощью полученной последовательности оптимальных параметров, формируя управляющие параметры для выполнения последовательности квантового алгоритма квантовой системой,
при этом упомянутые параметры включают в себя следующее: отстройка лазера от перехода несущей; отстройка лазера от перехода боковой полосы; длительность импульса; частота Раби, контролируемая интенсивностью лазерного импульса; параметр Лэмба-Дикке; частота электромагнитной ловушки;
передают последовательность оптимальных параметров выполнения физических операций в квантовую систему;
выполняют с помощью квантовой системы упомянутый квантовый алгоритм с помощью полученной последовательности оптимальных параметров выполнения физических операций, осуществляя управление ионами, электромагнитно захваченными в квантовой системе.
| US 11157827 B2, 26.10.2021 | |||
| WO 2021209745 A1, 21.10.2021 | |||
| US 20200219002 A1, 09.07.2020 | |||
| US 20200394547 A1, 17.12.2020 | |||
| СПОСОБ ВЫПОЛНЕНИЯ КВАНТОВЫХ ВЫЧИСЛЕНИЙ С ИСПОЛЬЗОВАНИЕМ КУДИТОВ | 2020 |
|
RU2761771C1 |
| СПОСОБ И УСТРОЙСТВО КВАНТОВОЙ ОБРАБОТКИ | 2016 |
|
RU2742504C2 |
Авторы
Даты
2024-11-12—Публикация
2022-12-23—Подача