Область техники, к которой относится изобретение.
Изобретение относится к способам формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов, при котором используют в качестве основы вычислений различные состояния набора кубитов на квантовом компьютере, выражающие вектор, при этом изменение ориентации вектора состояния кубитов реализуют при помощи квантовых вентилей, управляющие сигналы на квантовые вентили направляют с классического компьютера. Изобретение может быть использовано для произведения сложных вычислений, которые невозможно произвести на классических компьютерах.
В описании используются следующие термины:
Кубит – двухуровневая квантовая система, которой кодируется наименьшая единица информации в квантовом компьютере (аналог бита в обычном компьютере), использующаяся для квантовых вычислений. Кубит допускает два собственных состояния, обозначаемых  (обозначения Дирака), но при этом может находиться и в их суперпозиции.
(обозначения Дирака), но при этом может находиться и в их суперпозиции.
Квантовый вентиль – это базовый элемент квантового компьютера, преобразующий входные состояния кубитов на выходные по определённому закону, зависящему от физической реализации кубитов квантового процессора.
Вектор состояния кубита – вектор из двух комплексных чисел для описания состояния кубита. Вектор состояния кубита еще называют волновой функцией, и этот вектор может быть направлен в любую точку сферы Блоха. Сама сфера имеет единичный радиус, и это гарантирует, что для всех состояний сумма квадратов амплитуд будет равна единице.
Вектор состояния кубитов – вектор размерности n2 содержащий в себе коэффициенты суперпозиции базовых состояний n-кубитной системы, который описывает ее текущее квантовое состояние.
Уровень техники
Квантовый компьютер — вычислительное устройство, которое использует явления квантовой механики (квантовая суперпозиция, квантовая запутанность) для хранения, передачи и обработки данных. Квантовый компьютер (в отличие от классического) оперирует не битами (способными принимать значение либо 0, либо 1), а кубитами, значения которых представляют собой вектор - суперпозицию 0 и 1. Теоретически это позволяет обрабатывать все возможные состояния одновременно, достигая существенного преимущества (квантового превосходства) над обычными компьютерами в ряде алгоритмов.
Существует алгоритм нахождения собственных значений операторов (VQE - variational quantum eigensolver) - который позволяет на квантовых вычислителях решать узкий спектр задач гораздо эффективнее, сокращая сложность с экспоненциальной до полиномиальной. Данный алгоритм является гибридным квантовым алгоритмом, что подразумевает использование в ходе вычислений классического компьютера наряду с квантовым. Такой подход позволяет распределять части задачи между классическим и квантовым процессорами в зависимости от их специфики, достигая оптимального использования вычислительных ресурсов.
То есть для проведения вычислений требуется классический компьютер, который рассчитывает необходимые операции для их дальнейшей реализации квантовым процессором. Чтобы сделать итерацию вычислений на квантовом, нужно создать квантовое состояние каждый раз заново в неустойчивой к шумам квантовой среде, что технически сложно. Новое состояние создается квантовыми вентилями, которые математически представляются матрицами поворота (для спина, например) - мы воздействуем на систему кубитов по правилам квантового управления, а потом измеряем результат. В реальности матрицы поворота - это физические квантовые вентили, часть установки, которые снижают точность реализации из-за вносимого ими шума.
Из уровня техники известны способы формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов, например, способ, который описан в патенте на изобретение РФ № 2806840, опубликован в 2023 году.
В нем описан способ, при котором:
· используют в качестве основы вычислений различные состояния набора кубитов на квантовом компьютере, выражающие вектор, при этом
· изменение ориентации вектора состояния кубитов реализуют при помощи квантовых вентилей,
· управляющие сигналы на квантовые вентили направляют с классического компьютера, который также реализует шаг оптимизации для перерасчета параметров управляющих сигналов на квантовые вентили, при которых конечное значение математического ожидания гамильтониана состояния кубитов будет минимальным для решаемой задачи.
Данный способ является наиболее близким по технической сути и достигаемому техническому результату и выбран за прототип предлагаемого изобретения. Недостатком такого способа является то, что для решения задачи нахождения минимального математического ожидания гамильтониана состояния кубитов для решаемой задачи необходимо проделать множество итераций оптимизации как на классическом, так и на квантовом процессорах, для нахождения оптимальной конфигурации углов квантовых вентилей. Для этого исторически используются методы оптимизации первого порядка, такие как стохастический градиентный спуск или оптимизация Адама, или оптимизация второго порядка, типа BFGS и другие, однако все эти методы плохо работают с функцией, математическим ожиданием гамильтониана состояния кубитов, которая является целью оптимизации, и часто находят локальный, а не глобальный минимум. За счет длительного перебора стартовых точек оптимизации можно выявить, какая последовательность матриц поворота позволяет использовать алгоритм VQE относительно эффективно. В случае, если желаемая точность работы алгоритма не была достигнута, то добавляются дополнительные квантовые вентили, чтобы, по принципу «нового слоя», иметь возможность добавить оптимизационных степеней свободы.
Все это делает способ сложным, долгим и требует множества квантовых вентилей для управления состоянием кубитов.
Раскрытие изобретения.
Опирающееся на это оригинальное наблюдение настоящее изобретение, главным образом, имеет целью предложить способ формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов, при котором используют в качестве основы вычислений различные состояния набора кубитов на квантовом компьютере, выражающие вектор, при этом изменение ориентации вектора состояния кубитов реализуют при помощи квантовых вентилей, управляющие сигналы на квантовые вентили направляют с классического компьютера, который позволяет стабильно сокращать число шагов и повышать точность результата, а также сократить количество необходимых квантовых вентилей, что и является решаемой технической задачей.
Для достижения этой цели:
· управляющие сигналы на квантовые вентили направляют с классического компьютера, на котором происходит перерасчет параметров для обновления углов поворота спинов кубитов за счет римановской оптимизации, позволяющей рассчитать кратчайший путь до глобального минимума математического ожидания гамильтониана состояния кубитов, при этом
· на каждом шаге оптимизируют не отдельные параметры управляющего сигнала, а его матрицы поворотов векторов кубитов, которые рассматриваются как многообразие, и делают обратный пересчет на углы поворота векторов кубитов для формирования управляющего сигнала.
Благодаря данным новым характеристикам способа появляется возможность перебирать значения не вслепую, а сразу двигаться по кратчайшему пути к глобальному минимуму, существенно сокращая количество шагов оптимизации и, как следствие, количество требуемых квантовых вентилей. Действительно, римановская оптимизация позволяет рассматривает параметры матриц поворота как пространство многообразий, по которому происходит шаг градиентного спуска при поиске глобального минимума. Такой подход требует переноса классического описания многомерной оптимизации из Евклидова пространства в пространство многообразий.
Таким образом, параметры для обновления состояния квантовой схемы рассчитываются с учетом топологических свойств матриц, а не стандартными методами. Это и позволяет использовать меньше квантовых вентилей, чем в традиционном подходе.
Существует вариант изобретения, при котором для реализации шага оптимизации, а также расчета унитарных матриц применяют ротационное многообразие и спектральное линейное преобразование.
Благодаря таким данным выгодным характеристикам появляется возможность конкретизировать этап расчета унитарных матриц.
Существует еще один возможный вариант изобретения, в котором для реализации шага оптимизации, а также расчета унитарных матриц применяют ротационное многообразие и сингулярное линейное преобразование.
Благодаря таким данным выгодным характеристикам появляется возможность конкретизировать этап расчета унитарных матриц.
Существует и такой возможный вариант изобретения, в котором для реализации шага оптимизации, а также расчета эрмитовых матриц применяют многообразие Штифеля и сингулярное линейное преобразование.
Благодаря таким данным выгодным характеристикам появляется возможность конкретизировать этап расчета эрмитовых матриц.
Краткое описание чертежей.
Другие отличительные признаки и преимущества данного изобретения ясно вытекают из описания, приведенного ниже для иллюстрации и не являющегося ограничительным, со ссылками на прилагаемые рисунки, на которых:
- фигура 1 изображает стандартную схему для реализации способа формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов, уровень техники,
- фигура 2 изображает усовершенствованную схему, описываемую в данном документе, с отдельным блоком для римановской оптимизации, согласно изобретению.
На фигурах обозначены:
1 - квантовый процессор;
2 - классический компьютер (ЭВМ);
3 - цепь квантовых вентилей для подготовки состояния кубитов;
4 - блок измерения результата;
51 - блок пересчета шага параметрической оптимизации на классическом компьютере;
52 - блок выполнения римановской оптимизации на классическом компьютере для нахождения многообразия;
61 - блок пересчета обновления параметров квантовых вентилей;
62 - блок пересчета в углы квантовых вентилей;
7 - блок обновления параметров квантовых вентилей.
Осуществление изобретения.
Способ формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов осуществляют следующим образом.
Этап 1. Осуществляют подготовку стартового состояния кубитов, инициализация.
Этап 2. Собирают квантовую цепь, состоящую из квантовых вентилей, в соответствии с запланированной схемой. Квантовые вентили включают в себя такие как RX, RY, RZ, CNOT, CZ. Случайная инициализация параметров для квантовых вентилей для старта оптимизации.
Этап 3. Запускают квантовую цепь, реализуя новое квантовое состояние кубитов и составляющих Гамильтониана, производят измерение математического ожидания.
Этап 4. Осуществляют перерасчет параметров квантовых вентилей за счет реализации шага римановской оптимизации.
Этап 5. Шаг римановской оптимизации производят за счет ретракции – линейного разложения матриц, сдвига параметров и последующей нормировки матриц, сохраняющей их топологические свойства многообразия.
Этап 6. Осуществляют пересчет значений обновленных матриц в углы поворота для вентилей. Подготовка вентилей к следующему шагу.
Этап 7. Повторяют этапы начиная с первого этапа, до тех пор, пока не сработают условия останова оптимизации, например, пока градиент функции не перестанет значительно изменяться по модулю.
Этап 8. Проводят завершающие измерение для получения конечного значения математического ожидания Гамильтониана состояния кубитов.
Пример осуществления способа
Пример расчета задачи для Гамильтониана 6-кубитной системы.
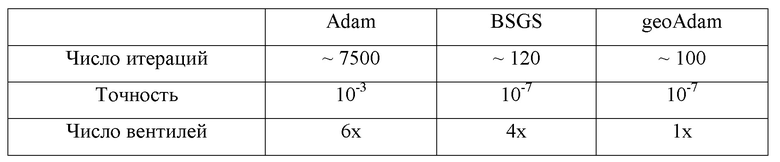
Таблица 1. Результаты многообразия Штифеля
Adam – это оптимизация методом Адама первого порядка, основанная на градиентном спуске.
geoAdam – это реализация римановской оптимизации для метода первого порядка, согласно изобретению.
BSGS – Алгоритм Бройдена - Флетчера - Гольдфарба - Шанно (Broyden–Fletcher–Goldfarb–Shanno algorithm) оптимизации второго порядка.
Промышленная применимость.
Предлагаемый способ формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов может быть осуществлен специалистом на практике и при осуществлении обеспечивает реализацию заявленного назначения, что позволяет сделать вывод о соответствии критерию «промышленная применимость» для изобретения.
Испытания предлагаемого способа квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов показали, что он позволяет повысить точность конечного значения матожидания и сократить число шагов, которые для этого требуются, при этом квантовых вентилей оказалось нужно значительно меньше.
При проведении испытаний было выяснено, что число итераций сокращается в сотни раз, точность вырастает на 4 порядка, а число квантовых вентилей сокращается в 3-10 раз в зависимости от размера схемы и числа кубитов.
Таким образом и достигается заявленный технический результат: возможность сократить количество необходимых квантовых вентилей, что упрощает создание физической квантовой установки, а кроме того при использовании предлагаемого способа на основе римановской оптимизации повышается точность измерения, снижается число итераций для сходимости алгоритма, что также является важными показателями для практического применения данной технологии.
Также можно сделать первичную оценку сокращения квантовых шумов при реализации данного алгоритма. Так как максимальная точность (quantum fidelity) сохранения сигнала после воздействия квантовым вентилем на кубит сохраняется максимум на 99,5%, а число необходимых вентилей уменьшено в среднем в 5 раз, то это даст повышение точности результата от 2,5%, что существенно для данной технологичной области.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И СИСТЕМА КОМПЕНСАЦИИ ШУМОВ НА КВАНТОВОМ ПРОЦЕССОРЕ С ПОМОЩЬЮ КВАНТОВОЙ ТОМОГРАФИИ ОПЕРАЦИЙ | 2022 |
|
RU2786349C1 |
| Квантовая вычислительная система на основе фотонных чипов | 2023 |
|
RU2806840C1 |
| Система и способ решения прикладных задач материаловедения с помощью сопряжения квантовых и классических устройств | 2023 |
|
RU2814969C1 |
| Архитектура квантовых вычислительных устройств для решения прикладных задач в области материаловедения | 2023 |
|
RU2821360C1 |
| СПОСОБ ПОЛУЧЕНИЯ УПРАВЛЯЮЩИХ ПАРАМЕТРОВ ДЛЯ КВАНТОВЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ НА ОСНОВЕ ИОНОВ В ЛОВУШКЕ, КОТОРЫЕ ЗАСТАВЛЯЮТ СИСТЕМУ МЕНЯТЬ СОСТОЯНИЯ, ЗАДАННЫЕ СОБСТВЕННЫМ ГАМИЛЬТОНИАНОМ, ТАК, ЧТО ЭВОЛЮЦИЯ В СИСТЕМЕ СООТВЕТСТВУЕТ ПРИМЕНЕНИЮ (ПОСЛЕДОВАТЕЛЬНОСТИ) ЛОГИЧЕСКИХ ОПЕРАЦИЙ | 2022 |
|
RU2830094C2 |
| СПОСОБ И УСТРОЙСТВО КВАНТОВОЙ ОБРАБОТКИ | 2016 |
|
RU2742504C2 |
| Встраиваемый в классический компьютер электронный блок и используемый в нём способ, основанный на квантовой процедуре счета | 2016 |
|
RU2632129C1 |
| СПОСОБ ВЫПОЛНЕНИЯ КВАНТОВЫХ ВЫЧИСЛЕНИЙ С ИСПОЛЬЗОВАНИЕМ КУДИТОВ | 2020 |
|
RU2761771C1 |
| СИСТЕМА АРХИТЕКТУРЫ КВАНТОВОГО КОМПЬЮТЕРА | 2022 |
|
RU2829117C2 |
| Управляющая система для квантовых вычислительных устройств | 2023 |
|
RU2814936C1 |

Изобретение относится к способу формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов. Технический результат заключается в возможности более эффективного формирования управляющих воздействий на квантовые вентили. В способе используют в качестве основы вычислений различные состояния набора кубитов на квантовом компьютере, выражающие вектор, при этом изменение состояния кубитов реализуют при помощи квантовых вентилей, управляющие сигналы на квантовые вентили направляют с классического компьютера, который также реализует шаг оптимизации для перерасчета параметров управляющих сигналов на квантовые вентили, при которых конечное значение математического ожидания гамильтониана состояния кубитов будет минимальным для решаемой задачи, при этом управляющие сигналы на квантовые вентили направляют с классического компьютера, на котором происходит перерасчет параметров для обновления углов поворота спинов кубитов за счет римановской оптимизации, позволяющей рассчитать кратчайший путь до глобального минимума математического ожидания гамильтониана состояния кубитов, при этом на каждом шаге оптимизируют не отдельные параметры управляющего сигнала, а его матрицы поворотов векторов кубитов, которые рассматриваются как многообразие, и делают обратный пересчет на углы поворота векторов кубитов для формирования управляющего сигнала. 3 з.п. ф-лы, 2 ил.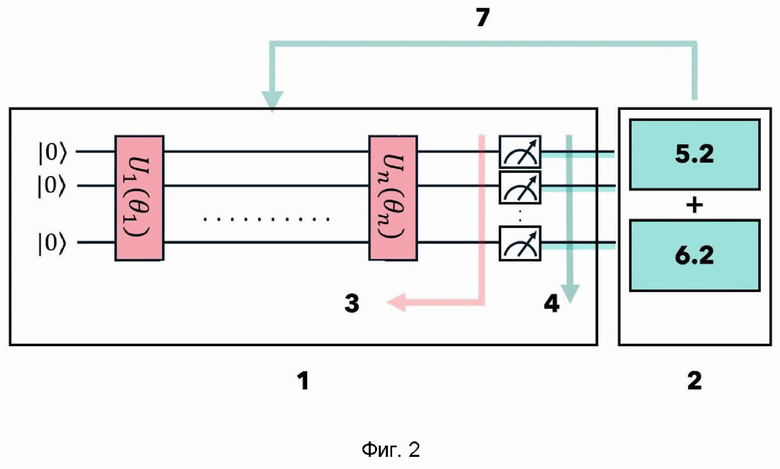
1. Способ формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов, при котором
• используют в качестве основы вычислений различные состояния набора кубитов на квантовом компьютере, выражающие вектор, при этом
• изменение состояния кубитов реализуют при помощи квантовых вентилей,
• управляющие сигналы на квантовые вентили направляют с классического компьютера, который
• также реализует шаг оптимизации для перерасчета параметров управляющих сигналов на квантовые вентили, при которых конечное значение математического ожидания гамильтониана состояния кубитов будет минимальным для решаемой задачи,
отличающийся тем, что
• управляющие сигналы на квантовые вентили направляют с классического компьютера, на котором происходит перерасчет параметров для обновления углов поворота спинов кубитов за счет римановской оптимизации, позволяющей рассчитать кратчайший путь до глобального минимума математического ожидания гамильтониана состояния кубитов, при этом
• на каждом шаге оптимизируют не отдельные параметры управляющего сигнала, а его матрицы поворотов векторов кубитов, которые рассматриваются как многообразие, и делают обратный пересчет на углы поворота векторов кубитов для формирования управляющего сигнала.
2. Способ по п.1, отличающийся тем, что для реализации шага оптимизации, а также расчета унитарных матриц применяют ротационное многообразие и спектральное линейное преобразование.
3. Способ по п.1, отличающийся тем, что для реализации шага оптимизации, а также расчета унитарных матриц применяют ротационное многообразие и сингулярное линейное преобразование.
4. Способ по п.1, отличающийся тем, что для реализации шага оптимизации, а также расчета эрмитовых матриц применяют многообразие Штифеля и сингулярное линейное преобразование.
| Квантовая вычислительная система на основе фотонных чипов | 2023 |
|
RU2806840C1 |
| СПОСОБ ВЫПОЛНЕНИЯ КВАНТОВЫХ ВЫЧИСЛЕНИЙ С ИСПОЛЬЗОВАНИЕМ КУДИТОВ | 2020 |
|
RU2761771C1 |
| US 10839306 B2, 17.11.2020 | |||
| US 20210279631 A1, 09.09.2021 | |||
| WO 2021173029 A1, 02.09.2021. | |||
Авторы
Даты
2024-09-02—Публикация
2023-12-08—Подача