Изобретение относится к измерительной технике квантовой магнитометрии и может быть использовано в составе бортовой аппаратуры подвижных носителей для дистанционного поиска магнитных аномалий, вызванных как естественными геологическими образованиями, так и наличием скрытых искусственных объектов под землей и в океанской среде.
Аналогом предлагаемого изобретения является способ измерения компонент магнитного поля на эффекте Ханле [Б.А. Андрианов, В.А. Белый, И.Е. Гринько, А.Ф. Лукошин, Квантовый магнитометр для измерения сверхслабых магнитных полей, Геофизическая аппаратура, вып. 57, 1975]. Измерительное устройство, реализующее этот способ, содержит оптический тракт, размещенный в центре трехкомпонентной системы катушек постоянного магнитного поля. Ориентационная зависимость амплитуды сигнала Ханле магнитометра используется в такой системе для градуировки токов компенсации, величины которых соответствуют трем компонентам измеряемого магнитного поля. Недостатком аналога является необходимость градуировки тока в магнитных катушках, которая приводит к измерительным погрешностям, связанным с влиянием не скомпенсированных компонент магнитного поля на форму и амплитуду детектируемого сигнала.
Аналогом предлагаемого способа, взятым за прототип, является способ измерения магнитного поля с помощью квантового магнитометра Мz типа путем измерения его резонансной частоты [Н.М.Померанцев, В.М.Рыжков, Г.В.Скроцкий Физические основы квантовой магнитометрии, Из-во Наука, М., 1972, 448 С.]. Недостатками аналога является его неработоспособность в условиях вариаций магнитного поля, не связанных с постоянным магнитным полем искомого магнитного объекта. Так, например, вариации геомагнитного поля, вызванные в период солнечной активности (период магнитных бурь) достигают амплитуд в несколько сотен нТл, что на 4-5 порядков превышает вариационную чувствительность современных МZ магнитометров, и делает их неспособными обнаруживать магнитный объект, магнитное поле которого составляет порядок величины этой чувствительности.
Задачей предлагаемого способа является измерение координат магнитного объекта в условиях вариаций геомагнитного поля путем одновременного измерения разности резонансных частот двух МZ магнитометров в составе движущегося квантового градиентометра с фиксированной базой, размещенного в плоскости, параллельной плоскости, в которой расположен искомый магнитный объект. При определенной ориентации базы градиентометра относительно направления его движения работоспособность способа не зависит от ориентации магнитного момента объекта относительно базы градиентометра. При этом точность измерения координат искомого магнитного объекта определяется предельной чувствительностью квантовых магнитометров и не зависит от вариаций магнитного поля, не связанного с магнитным объектом.
Поставленная задача достигается тем, что в известном способе измерения координат магнитного диполя, основанным на измерении резонансной частоты первого Мz квантового магнитометра с оптической накачкой, размещенного в начале оси ОZ в первой плоскости ZY декартовой системы координат ZХY, параллельной второй плоскости Z*Y* декартовой системы координат Z*Х*Y*, в которой расположен магнитный диполь, причем ось ОХ совпадает с осью ОХ*, ось ОY параллельна оси ОY* и ось ОZ параллельна оси ОZ*, на расстоянии d по оси ОХ от первого Мz квантового магнитометра в третьей плоскости Z**Y** декартовой системы координат Z**Х**Y**, параллельной первой ZY и второй Z*Y* плоскостям систем координат ZХY и Z*Х*Y* соответственно, размещается второй Мz квантовый магнитометр, образуя квантовый градиентометр с базой d, которая направлена вдоль оси ОХ, причем ось ОХ** совпадает с осью ОХ*, ось ОY** параллельна оси ОY* и ось ОZ** параллельна оси ОZ*, а первая плоскость ZY декартовой системы координат ZХY размещена между второй плоскостью Z*Y* и третьей плоскостью Z**Y**, далее с постоянной одинаковой скоростью первый и второй Мz магнитометры перемещаются в плоскости ХZ соответственно вдоль осей ОZ и ОZ** на равные расстояния, которым соответствует максимальная разность частот ∆ω1 первого и второго Мz магнитометров и определяет Z координату магнитного диполя,
далее с постоянной одинаковой скоростью первый и второй Мz магнитометры перемещаются в плоскости, отстоящей от плоскости XY на расстояние Z координаты магнитного диполя, соответственно, в направлении осей ОY и ОY** на равные расстояния, которым соответствует максимальная разность частот ∆ω2 первого и второго Мz магнитометров и определяет Y координату магнитного диполя,
далее из отношения ∆ω2/∆ω1 и по измеренным значениям Z и Y координат магнитного диполя вычисляется его Х координата вдоль оси ОХ.
Сущность предлагаемого способа измерения геомагнитного поля поясняется графическим материалом на фиг.1, фиг.2, фиг.3 и фиг.4.
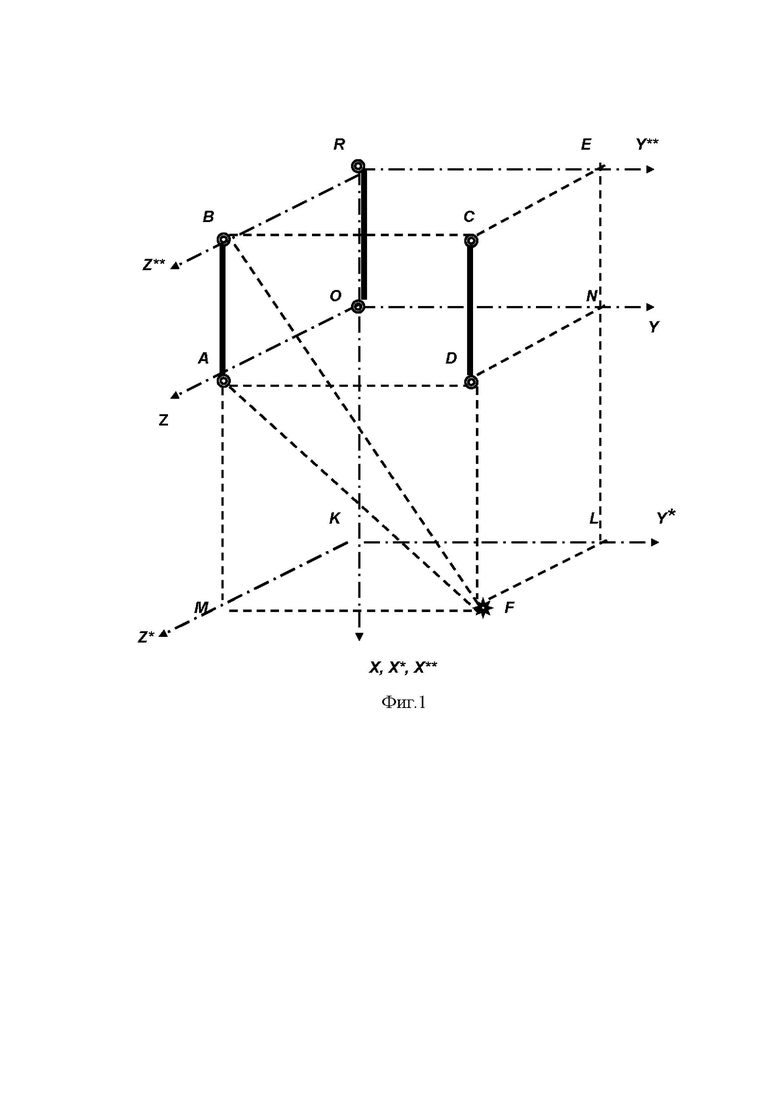
На фиг.1 изображена схема перемещения квантового градиентометра в декартовой системе координат ХYZ.
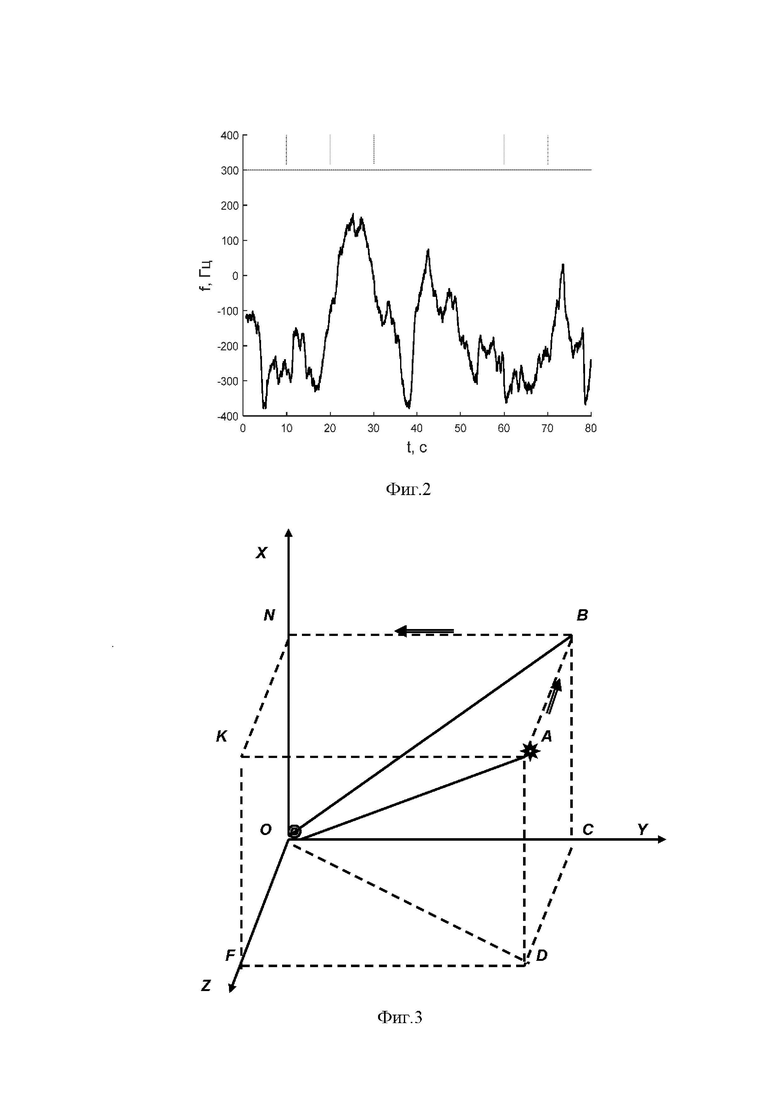
На фиг.2 представлена осциллограмма экспериментальной записи вариаций лабораторного магнитного поля, выраженных в единицах частоты радиооптического резонанса в оптически ориентированных атомах цезия.
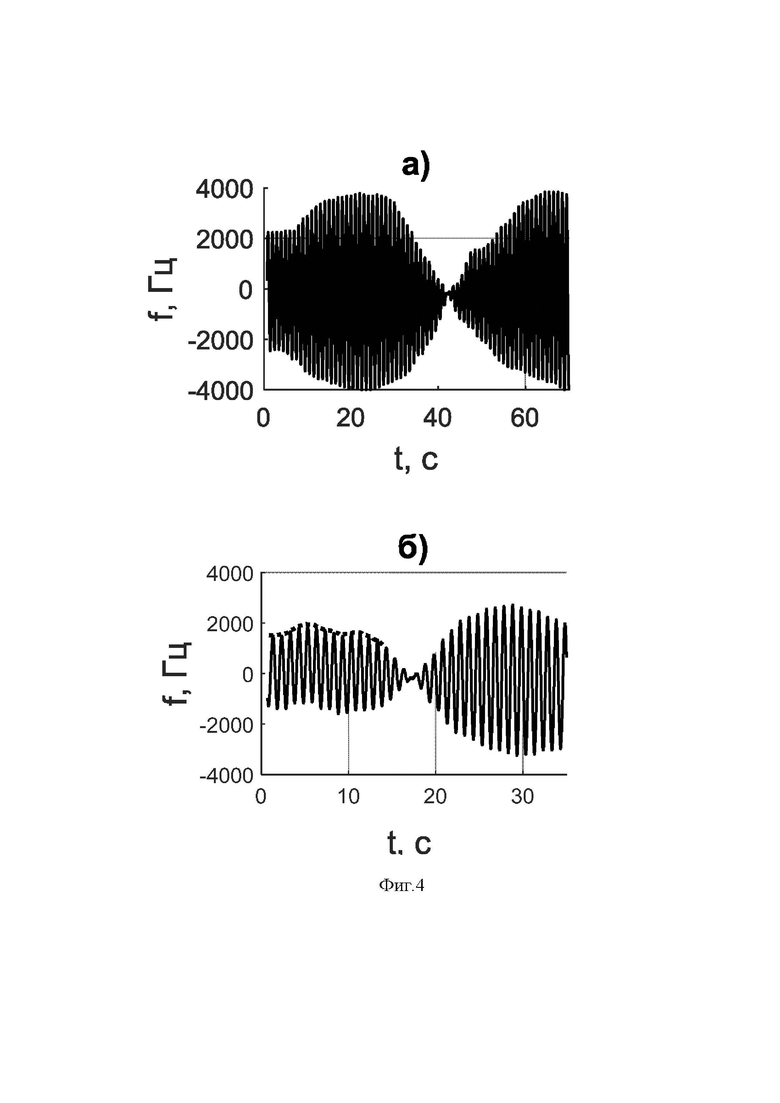
На фиг.3 изображена схема перемещения соленоида (макета магнитного диполя) относительно квантового магнитометра, размещенного в начале декартовой системе координат ХYZ.
На фиг. 4 изображены осциллограммы вариаций частоты квантового магнитометра при движении соленоида по прямолинейной траектории: а) вдоль направления АВ б) вдоль направления ВN. Пунктиром обозначена огибающая вариаций лабораторного магнитного поля, не связанных с вариациями магнитного поля соленоида, создаваемых в зоне размещения магнитометра.
На фиг.1 введены следующие обозначения:
F – точка размещения магнитного диполя в системе координат XYZ;
OA - Z координата магнитного диполя;
ON - Y координата магнитного диполя;
OK - X координата магнитного диполя;
AB = СD = OR = d - ось (база) градиентометра.
Перемещение первого квантового магнитометра осуществляется в плоскости AOND, перемещение второго квантового магнитометра осуществляется в плоскости RBCE, точечный магнитный диполь размещен в плоскости KMFL, параллельной плоскостям AOND и RBCE,
В точках А, В, С, D создаются соответственно магнитные поля диполя НА, НВ, НС, НD.
На фиг.3 введены следующие обозначения:
O – точка размещения квантового магнитометра;
OF - Z координата магнитного диполя;
ОC - Y координата магнитного диполя;
ОN - X координата магнитного диполя.
В соответствии с формулой изобретения в начальный момент времени первый квантовый Мz магнитометр с оптической накачкой, размещается в начале оси ОZ в первой плоскости ZY декартовой системы координат ZХY, параллельной второй плоскости Z*Y* декартовой системы координат Z*Х*Y*, в которой расположен магнитный диполь, причем ось ОХ совпадает с осью ОХ*, ось ОY параллельна оси ОY* и ось ОZ параллельна оси ОZ* (см. фиг.1).
В этот же начальный момент времени на расстоянии d по оси ОХ от первого Мz квантового магнитометра в третьей плоскости Z**Y** декартовой системы координат Z**Х**Y**, параллельной первой ZY и второй Z*Y* плоскостям систем координат ZХY и Z*Х*Y* соответственно, размещается второй Мz квантовый магнитометр, образуя квантовый градиентометр с базой d, которая направлена вдоль оси ОХ, причем ось ОХ** совпадает с осью ОХ*, ось ОY** параллельна оси ОY* и ось ОZ** параллельна оси ОZ*, а первая плоскость ZY декартовой системы координат ZХY размещена между второй плоскостью Z*Y* и третьей плоскостью Z**Y**.
Предполагается, что в начальный момент времени магнитное поле, наводимое магнитным диполем в зоне размещения первого и второго Мz квантового магнитометров много меньше их вариационной чувствительности. В этом случае резонансная частота первого Мz квантового магнитометра равна резонансной частоте второго Мz квантового магнитометра и определяется значением напряженности геомагнитного поля и его вариациями. Равенство резонансных частот первого и второго Мz квантовых магнитометров выполняется с погрешностью, равной величине магнитного градиента геомагнитного поля, то есть разности напряженности геомагнитного поля в пределах расстояния d. При величине d = 10 см разность напряженности геомагнитного поля на поверхности Земли вдоль оси ОХ декартовой системы координат ZХY не превышает 10-9 эрстед [Магнитное поле Земли. Напряженность магнитного поля у поверхности и на больших высотах dpva.ru› Физический справочник›…/NapruagMagneticEarth]. Тот же порядок величины градиент геомагнитного поля имеет на поверхности планеты в плоскости магнитного меридиана. Указанная выше разность на два порядка меньше вариационной чувствительности Мz квантовых магнитометров, что обуславливает равенство их резонансных частот в геомагнитном поле в случае отсутствия каких-либо магнитных аномалий (как например, залежей железной руды). Таким образом, вариации геомагнитного поля, вызванные солнечной активностью, будут вносить идентичный вклад в вариации частоты первого и второго квантового магнитометра, что автоматически приводит к нулевой разности их частот, либо незначительному постоянному значению этой разности, обусловленному различием параметров составных элементов первого и второго магнитометров (например, источников накачки и резонансных камер поглощения).
С учетом сказанного выше в начальный момент времени разность частот первого и второго магнитометров в условиях вариаций геомагнитного поля и при достаточном удалении от магнитного диполя близка к нулевому значению. Далее, в соответствии с формулой изобретения и фиг.1 осуществляется движение с постоянной одинаковой скоростью первого и второго Мz магнитометров соответственно вдоль осей ОZ и ОZ** на равные расстояния ОА и RB, при которых достигается максимальная разность частот ∆ω1 первого и второго Мz магнитометров. При этом перпендикуляр FA к оси ОZ и перпендикуляр ВF к оси ОZ** соответствуют кратчайшему расстоянию от магнитометров до магнитного диполя и определяют отрезок ОА как его Z координату.
Далее, согласно формуле изобретения и фиг.1, первый и второй Мz магнитометры перемещаются в плоскости, отстоящей от плоскости XY на расстояние Z координаты магнитного диполя, соответственно в направлении осей ОY и ОY** на равные расстояния АD и ВC, которым соответствует максимальная разность частот ∆ω2 первого и второго Мz магнитометров. При этом перпендикуляры DF и СF к плоскости МКFL системы координат Z*Х*Y*, в которой расположен магнитный диполь, соответствуют кратчайшему расстоянию от магнитометров до магнитного диполя и определяют отрезок АD как его Y координату.
Далее, согласно формуле изобретения, из отношения ∆ω2/∆ω1 и по измеренным значениям Z и Y координат магнитного диполя вычисляется его Х координата вдоль оси ОХ. Процедура вычислений подразумевает аппроксимацию зависимости напряженности магнитного поля диполя Нд на некотором расстоянии r в виде:
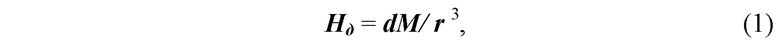
где dM - магнитный момент диполя.
Из фиг. 1 следует, что с учетом аппроксимации (1) разность магнитного поля диполя ∆Нд1 в точкаx А и В равна:
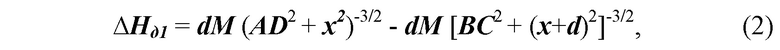
где x - Х координата магнитного диполя в системе координат ZХY.
Из фиг. 1 также следует, что с учетом аппроксимации (1) разность магнитного поля диполя ∆Нд2 в точкаx D и С равна:
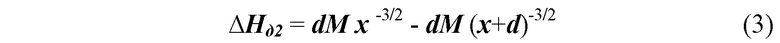
Разности частот первого и второго магнитометров ∆ω2 и ∆ω1 связаны с ∆Нд1 и ∆Нд2 равенствами:
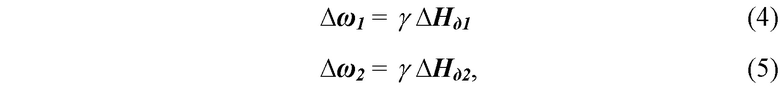
где 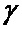 - гиромагнитное отношение атомов рабочего вещества квантовых магнитометров.
- гиромагнитное отношение атомов рабочего вещества квантовых магнитометров.
Таким образом, Х координата магнитного диполя может быть определена на основе решения следующего уравнения:
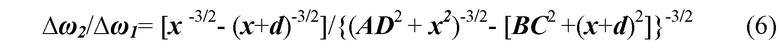
В предлагаемом способе принципиально исключена его неработоспособность в виде мертвых зон, поскольку ось d ортогональна плоскости АОND - плоскости поверхности Земли - в отличие от варианта, в котором вектор d лежит в этой плоскости. Так, например, при ориентации вектора d вдоль оси ОY и при условии размещения магнитного диполя в плоскости АМКО движение центра базы градиентометра d вдоль оси ОZ не приводит к вариации разности частот квантовых магнитометров, что эквивалентно отсутствию информации о координатах магнитного диполя.
Для проверки работоспособности предложенного способа измерения геомагнитного поля и его компонент, а также для оценки измерительной погрешности авторами заявки был осуществлен эксперимент с макетом квантового МZ магнитометра на парах цезия. Проведение эксперимента осуществлялось в лабораторных условиях, которые радикально отличаются от условий реализации предлагаемого способа на практике при поиске магнитных аномалий в геомагнитном поле испытательного полигона. В соответствии с описанием предлагаемого способа подобный поиск предполагает движение квантового градиентометра на подвижной немагнитной платформе вблизи места локализации магнитного объекта. В момент прохождения платформы вблизи аномалии разность частот квантовых магнитометров в составе единого модуля максимально изменяется, причем знак этого изменения зависит от ориентации объекта в геомагнитном пространстве.
В лабораторных условиях, где присутствуют различные приборы и металлические конструкции, однородность магнитного поля существенно зависит от координаты размещения квантовых магнитометров, что делает невозможным поиск магнитного объекта путем изменения положения магнитометров в пространстве лаборатории. Для преодоления этой трудности, а также упрощения процедуры измерений, в наших экспериментах использовался один МZ магнитометр, размещенный в точке О неподвижной декартовой системы координат ZХY, (фиг.3), который фиксировал магнитное поле точечного диполя в процессе его движения относительно магнитометра. В качестве макета точечного диполя использовался миниатюрный соленоид, питаемый переменным током на частоте 10 Гц. Для ослабления влияний вариаций лабораторного магнитного поля на проводимые измерения амплитуда вариаций магнитного поля, создаваемого соленоидом в зоне размещения магнитометра, десятикратно превышала максимальную амплитуду вариаций лабораторного магнитного поля. Величина амплитуды вариаций в единицах резонансной частоты магнитометра ∆ω1 и ∆ω2 зависела от расстояния от соленоида до магнитометра и направления движения соленоида (см. фиг. 4), что соответствовало схеме измерений вариаций резонансной частоты двух квантовых магнитометров предлагаемым способом. В начальный момент времени соленоид размещался в фиксированной точке А системы координат ZХY, (фиг.3), в которой магнитометр регистрировал вариации лабораторного магнитного поля, показанные на осциллограмме фиг. 2 .При этом, в силу относительно большого расстояния 0А (порядка 10 метров), влияние магнитного поля соленоида на вариации частоты магнитометра было незначительным.
По мере движении соленоида по траектории АВ (фиг.3) переменное магнитное поле соленоида возрастало и достигала максимального значения в точке В, которая соответствовало расстоянию АВ между соленоидом и магнитометром. При этом регистрировался сигнал, осциллограмма которого представлена на фиг.4б и, в соответствии с описанием изобретения, определялась Z координата магнитного диполя в системе координат ZХY (фиг.3), равная в нашем эксперименте 10 метров. Далее соленоид перемещался по траектории ВN до точки N, которая соответствовала кратчайшему расстоянию ОN между соленоидом и магнитометром по оси ОХ в системе координат ZХY фиг.3. При этом регистрировался сигнал, осциллограмма которого представлена на фиг.4а и, в соответствии с описанием изобретения, определялась Y координата магнитного диполя в системе координат ZХY фиг.3, равная в нашем эксперименте 1 метру. Далее по измеренным амплитудам вариаций магнитного поля на осциллограммах фиг.4 вычислялось отношение резонансной частоты магнитометра ∆ω2 к ∆ω1, которое согласно формуле изобретения и фиг. 3 было равно:
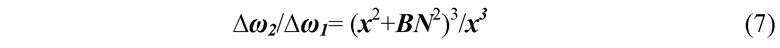
Из решения уравнения (7) определялась Х координата магнитного диполя в системе координат ZХY фиг.3, равная в нашем эксперименте 1 метру. При этом относительная погрешность измерений Х и Y координат соленоида составляла порядок величины 10% и определялась вариациями лабораторного магнитного поля в соответствии с фиг.2 (на фиг. 3 эти вариации отчетливо видны на фоне записи сигнала магнитометра).
Вариационная чувствительность используемого в эксперименте квантового магнитометра для наших экспериментальных условий составляла величину 0,014 нТл в полосе регистрации 1Гц. При установке точно такого же такого магнитометра в измерительном модуле градиентометра указанную выше погрешность можно существенно уменьшить. Так, например, с учетом зависимостей (1), (4) и (5), ожидаемая относительная погрешность измерений координат магнитного объекта на расстоянии 1 метр до измерительного модуля в проводимом эксперименте не должна превышать величины 1%, а при двукратном сокращении этого расстояния (например, в варианте поиска магнитных взрывоопасных объектов) значение измерительной погрешности может составлять менее 0,1%.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ измерения геомагнитного поля на движущихся и вращающихся носителях | 2024 |
|
RU2825539C1 |
| Градиентометр | 1978 |
|
SU789949A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СТАЦИОНАРНОГО ГЕОМАГНИТНОГО ПОЛЯ ПРИ ПРОВЕДЕНИИ МОРСКОЙ МАГНИТНОЙ СЪЕМКИ | 2010 |
|
RU2433427C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ИНДУКЦИИ ГЕОМАГНИТНОГО ПОЛЯ С ПОДВИЖНОГО ОБЪЕКТА | 2003 |
|
RU2236029C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СТАЦИОНАРНОГО ГЕОМАГНИТНОГО ПОЛЯ ПРИ ПРОВЕДЕНИИ МОРСКОЙ МАГНИТНОЙ СЪЕМКИ | 2007 |
|
RU2331090C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СТАЦИОНАРНОГО ГЕОМАГНИТНОГО ПОЛЯ ПРИ ПРОВЕДЕНИИ МОРСКОЙ МАГНИТНОЙ СЪЕМКИ | 2010 |
|
RU2433429C2 |
| Способ определения напряженности магнитного поля дипольного источника | 1984 |
|
SU1267306A1 |
| Способ спутниковой гравитационной градиентометрии | 2020 |
|
RU2745364C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ УГЛОВОГО ПОЛОЖЕНИЯ БУРОВОЙ СКВАЖИНЫ (ЕГО ВАРИАНТЫ) | 2004 |
|
RU2261324C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОМПОНЕНТ ГЕОМАГНИТНОГО ПОЛЯ | 1986 |
|
SU1426256A1 |
Изобретение относится к измерительной технике. Сущность способа измерения координат магнитного диполя заключается в том, что осуществляют измерение координат магнитного объекта в условиях вариаций геомагнитного поля путем одновременного измерения разности резонансных частот двух магнитометров в составе движущегося квантового градиентометра с фиксированной базой, размещенного в плоскости, параллельной плоскости, в которой расположен искомый магнитный объект. При определенной ориентации базы градиентометра относительно направления его движения работоспособность способа не зависит от ориентации магнитного момента объекта относительно базы градиентометра. Технический результат – повышение точности измерения координат искомого магнитного объекта. 4 ил.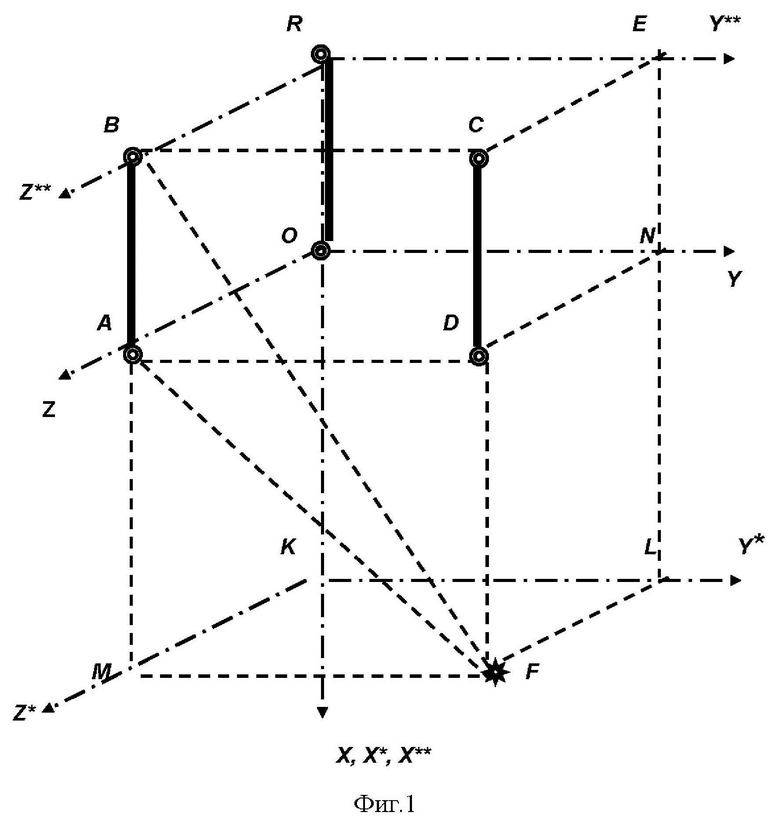
Способ измерения координат магнитного диполя, размещенного в геомагнитном поле, основанный на измерении резонансной частоты первого Мz квантового магнитометра с оптической накачкой, размещенного в начале оси 0Z в первой плоскости ZY декартовой системы координат ZХY, параллельной второй плоскости Z*Y* декартовой системы координат Z*Х*Y*, в которой расположен магнитный диполь, причем ось ОХ совпадает с осью ОХ*, ось ОY параллельна оси ОY* и ось ОZ параллельна оси ОZ*, отличающийся тем, что на расстоянии d по оси ОХ от первого Мz квантового магнитометра в третьей плоскости Z**Y** декартовой системы координат Z**Х**Y**, параллельной первой ZY и второй Z*Y* плоскостям систем координат ZХY и Z*Х*Y* соответственно, размещается второй Мz квантовый магнитометр, образуя квантовый градиентометр с базой d, которая направлена вдоль оси ОХ, причем ось ОХ** совпадает с осью ОХ*, ось ОY** параллельна оси ОY* и ось ОZ** параллельна оси ОZ*, а первая плоскость ZY декартовой системы координат ZХY размещена между второй плоскостью Z*Y* и третьей плоскостью Z**Y**,
далее с постоянной одинаковой скоростью первый и второй Мz магнитометры перемещаются в плоскости ХZ соответственно вдоль осей ОZ и ОZ** на равные расстояния, которым соответствует максимальная разность частот 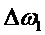 первого и второго Мz магнитометров и определяет Z координату магнитного диполя,
первого и второго Мz магнитометров и определяет Z координату магнитного диполя,
далее с постоянной одинаковой скоростью первый и второй Мz магнитометры перемещаются в плоскости, отстоящей от плоскости XY на расстояние Z координаты магнитного диполя, соответственно в направлении осей ОY и ОY** на равные расстояния, которым соответствует максимальная разность частот 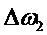 первого и второго Мz магнитометров и определяет Y координату магнитного диполя,
первого и второго Мz магнитометров и определяет Y координату магнитного диполя,
далее из отношения 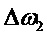 /
/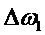 и по измеренным значениям Z и Y координат магнитного диполя вычисляется его Х координата вдоль оси ОХ.
и по измеренным значениям Z и Y координат магнитного диполя вычисляется его Х координата вдоль оси ОХ.
| Устройство для определения координат и магнитного момента дипольного источника поля | 1987 |
|
SU1437812A1 |
| СПОСОБ ЛАЗЕРНОГО ОТДЕЛЕНИЯ ЭПИТАКСИАЛЬНОЙ ПЛЕНКИ ИЛИ СЛОЯ ЭПИТАКСИАЛЬНОЙ ПЛЕНКИ ОТ РОСТОВОЙ ПОДЛОЖКИ ЭПИТАКСИАЛЬНОЙ ПОЛУПРОВОДНИКОВОЙ СТРУКТУРЫ (ВАРИАНТЫ) | 2011 |
|
RU2469433C1 |
| Способ определения магнитного момента дипольного источника поля и координат этого источника | 1985 |
|
SU1322208A1 |
| CN 112611310 A, 06.04.2021. | |||
Авторы
Даты
2024-03-21—Публикация
2023-12-27—Подача