Изобретение относится к области цифровой обработки и анализа данных и предназначено для классификации сигналов фМРТ головного мозга на отсутствие или наличие большого депрессивного расстройства (БДР). Технический результат может найти применение в программно-аппаратных комплексах для диагностики БДР, а также в комплексе программ для анализа сетевых данных нейрофизиологической и/или иной природы.
Ранняя диагностика большого депрессивного расстройства жизненно необходима для пациентов, страдающих тяжелыми и необратимыми последствиями депрессии. Анализ функциональной связности, основанный на данных фМРТ, может предоставить ценные биомаркеры для клинической диагностики БДР. Данные фМРТ представляют собой корреляционные матрицы, которые могут быть интерпретированы как матрицы смежности графов и классифицированы методами на основе искусственных нейронных сетей. Графовые нейронные сети (ГНС) были введены специально для решения задач, связанных с обработкой графовых данных. Внутренние свойства графовых данных накладывают большие ограничения на существующие методы машинного обучения и искусственного интеллекта. При анализе графовых данных необходимо учитывать структуру связей между узлами графа, свойства узлов и рёбер графа, существование зависимости между узлами и т.д.
Известна ансамблевая модель на основе ГНС для классификации БДР [1]. Модель достигла точности 73% на данных фМРТ 821 испытуемого с диагностированным БДР и 765 испытуемых контрольной группы. В подходе [1] авторам удалось решить проблему переобучения ГНС за счет использования перекрестной проверки, однако скорость обучения не была принята во внимание. Также авторам не удалось достичь эффективности классификации БДР по сравнению с другими подходами.
В решении [2] проблема постановки диагноза БДР была сформулирована как задача классификации графов. Набор данных фМРТ включал 1300 испытуемых с диагностированным БДР и 1128 испытуемых контрольной группы. Была построена графовая нейронная сеть, результат классификации которой превзошел такие нейросетевые подходы, как многослойный персептрон, машину опорных векторов, дерево решений, и составил 67,43% по метрике F1.
Недостатками указанных решений является невозможность их применения в случае недостаточного объёма исследуемой выборки, позволяющего корректно обучить искусственную нейронную сеть. Кроме того, указанные способы продемонстрировали недостаточно высокую точность классификации данных фМРТ, имеющих графовую структуру.
Предлагаемое техническое решение свободно от упомянутых недостатков: способ графовой нейросетевой классификации имеет более высокую точность по сравнению с известными решениями [1, 2] и может использоваться на относительно малых и несбалансированных выборках. Предлагаемое техническое решение отличается тем, что способ графовой нейросетевой классификации на отсутствие или наличие большого депрессивного расстройства по данным фМРТ включает анализ топологических свойств обрабатываемых данных фМРТ, что напрямую влияет на сходимость процесса обучения, вычислительные затраты и точность классификации. Предлагаемое техническое решение разработано для классификации данных фМРТ, интерпретируемых как графовые данные, которые недостаточно эффективно классифицируются с использованием других методов глубокого обучения.
Известно, что несмотря на высокую эффективность ГНС в обработке графовых данных, существует ограничение на количество слоёв в архитектуре ГНС, значительно снижающее качество классификации. Ограничение обусловлено тем, что операция свёртки в графовых сверточных сетях является частным случаем Лапласовского сглаживания, многократное применение которого приводит к схождению характеристик узлов графа к аналогичным значениям [3]. Предлагаемый способ основан на снижении количества связей в исходном наборе данных путём применения пороговых значений с целью снижения избыточности подаваемых данных и контроля переобучения, а также на использовании кратчайшего пути как параметра, определяющего оптимальное количество свёрточных слоев в ГНС для обрабатываемого набора данных.
Техническим результатом, обеспечиваемым приведенной совокупностью признаков, является подбор оптимизированной архитектуры графовой нейронной сети для классификации данных фМРТ, интерпретируемых как графовые данные. Архитектура ГНС с наиболее оптимальным результатом классификации графовых данных определяется топологическими свойствами обрабатываемых данных, выявляемых с помощью статистического анализа топологий графов. Также технический результат достигается тем, что исходный набор данных подвергается процедуре прореживания с помощью набора пороговых значений для весов узлов. Для полученных наборов данных после применения пороговых значений считаются распределения кратчайших путей, после чего полученные распределения анализируются с помощью статистического критерия для независимых выборок для получения наиболее значимого значения длины кратчайшего пути, имеющего наиболее высокое значение статистики.
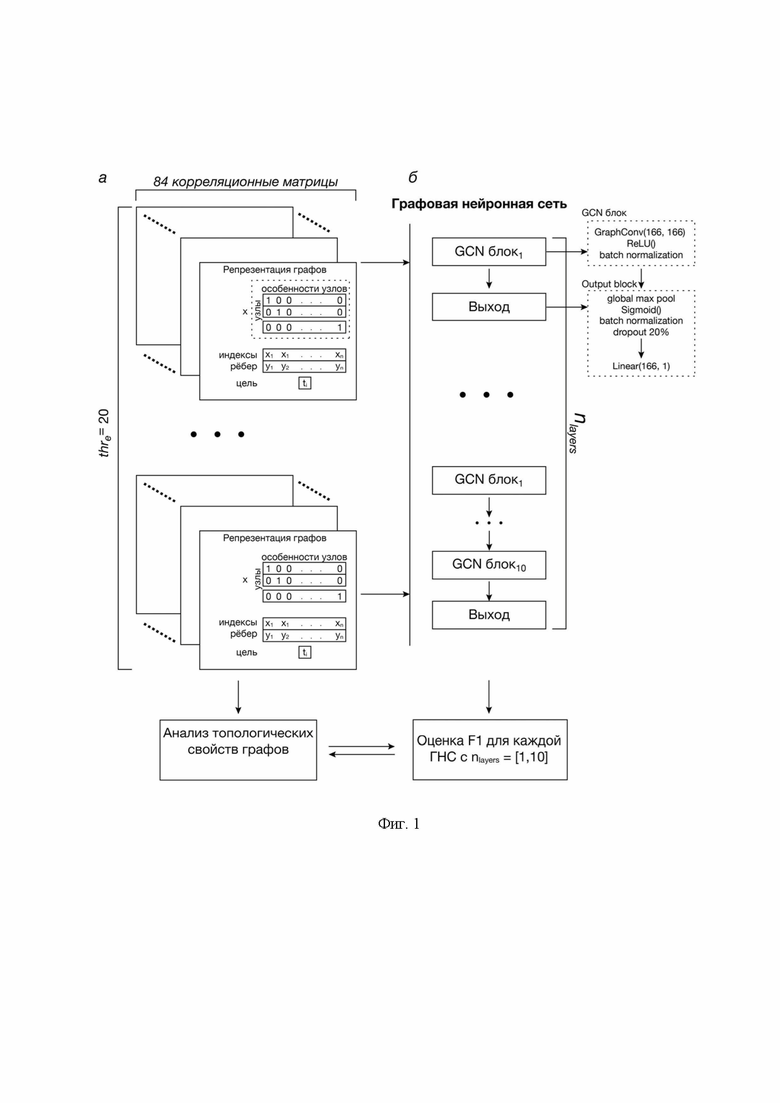
Предлагаемый способ поясняется чертежами. На фиг. 1 представлена общая схема предлагаемого способа графовой нейросетевой классификации на отсутствие или наличие большого депрессивного расстройства по данным фМРТ. На фиг. 1А показан способ репрезентации графовых данных для обучения ГНС, где количество наборов данных равняется 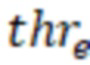 = 20 - числу применяемых пороговых значений. На фиг. 1B показана схема обучения ГНС для полученных наборов данных. На фиг. 2 показаны изменения в распределениях степеней исходного набора данных в зависимости от применяемого значения
= 20 - числу применяемых пороговых значений. На фиг. 1B показана схема обучения ГНС для полученных наборов данных. На фиг. 2 показаны изменения в распределениях степеней исходного набора данных в зависимости от применяемого значения 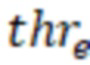 . На фиг. 3 показаны изменения в распределениях кратчайших путей в зависимости от применяемого значения
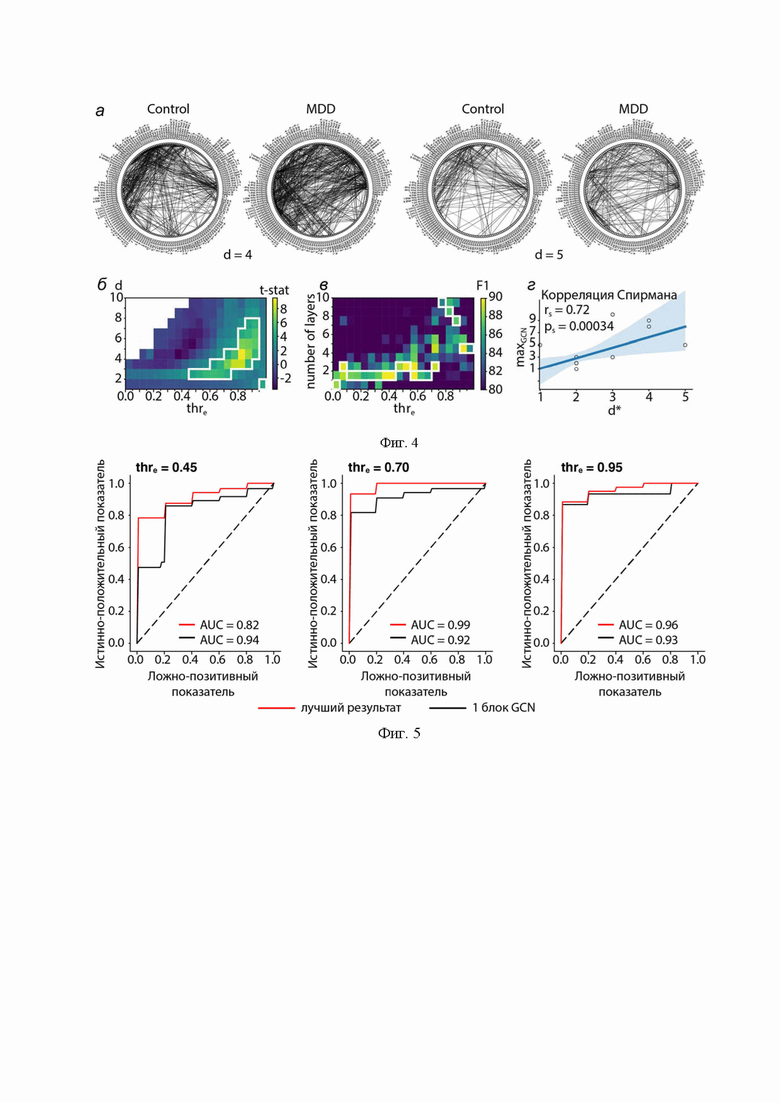
. На фиг. 3 показаны изменения в распределениях кратчайших путей в зависимости от применяемого значения 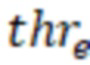 . На фиг. 4 показаны: A - зависимость значения t-статистики от значения длины кратчайшего пути d и величины порога
. На фиг. 4 показаны: A - зависимость значения t-статистики от значения длины кратчайшего пути d и величины порога 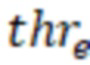 ; B - зависимость значения метрики F1 от количества слоёв в рассматриваемой ГНС (параметр number of layers) и величины порога
; B - зависимость значения метрики F1 от количества слоёв в рассматриваемой ГНС (параметр number of layers) и величины порога 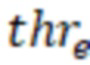 ; С - корреляция между количеством слоёв в ГНС с наибольшим F1 для каждого порога и длины кратчайшего пути с наибольшей t-статистикой (p < 0,05). На фиг. 5 показаны кривые ROC для трех
; С - корреляция между количеством слоёв в ГНС с наибольшим F1 для каждого порога и длины кратчайшего пути с наибольшей t-статистикой (p < 0,05). На фиг. 5 показаны кривые ROC для трех 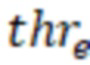 = [0,45, 0,70, 0,95] для двух случаев: модель ГНС с 1 блоком GCN (черная кривая) и модель ГНС с лучшей производительностью (красная кривая), архитектура которой подобрана в соответствии с предлагаемым способом.
= [0,45, 0,70, 0,95] для двух случаев: модель ГНС с 1 блоком GCN (черная кривая) и модель ГНС с лучшей производительностью (красная кривая), архитектура которой подобрана в соответствии с предлагаемым способом.
Предлагаемый способ осуществляется следующим образом.
На первом этапе регистрируют сигнал функциональной МРТ головного мозга в состоянии покоя у испытуемых контрольной группы и испытуемых с диагностированным большим депрессивным расстройством. На фиг. 1 представлено схематическое изображение предлагаемого способа на примере классификации корреляционных матриц фМРТ двух групп испытуемых. Исходные данные представляют собой 84 корреляционные матрицы фМРТ: 49 матриц испытуемых контрольной группы (Control), 35 матриц испытуемых с большим депрессивным расстройством (MDD). Корреляционные матрицы фМРТ строятся в соответствии с автоматическим атласом анатомической разметки AAL3 и имеют размер 166*166. Каждый элемент корреляционной матрицы хранит в себе коэффициент корреляции Пирсона (фиг. 1(а)). Здесь x - набор характеристик узла. Поскольку каждый узел в корреляционной матрице представляет одну область мозга, этот набор был представлен в виде матрицы 166х166, где первое измерение соответствует каждому узлу, а второе - признакам. Такая формулировка обозначает, что каждый узел уникален и имеет отдельный признак, без указания характера признака. Поле индексы ребер представляет собой двумерный массив, содержащий ребра корреляционной матрицы в координатном формате. Значения в первой и второй строке являются индексами исходящих и входящих узлов, соответственно. Наконец, одноэлементный массив цель содержит метку текущего графа, которая в задаче бинарной классификации была либо 0, либо 1. В данном примере, метка 0 была присвоена классу MDD, а метка 1 - классу Control.
На втором этапе каждая корреляционная матрица фМРТ проходит через процедуру прореживания, заключающуюся в том, что к значениям коэффициента Пирсона в корреляционных матрицах применяется пороговое значение, при этом все значения в матрице ниже порогового приравниваются к нулю. Применение пороговых значений позволяет отбросить наименее значимые связи и снизить избыточность в данных, на которых обучается ГНС, что позволяет контролировать переобучение. В данном решении предлагается применение 20 пороговых значений 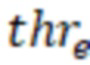 от 0,0 до 0,95 с шагом 0,05. В результате из исходной корреляционной матрицы получается 20 наборов матриц (смежности) разной степени разреженности.
от 0,0 до 0,95 с шагом 0,05. В результате из исходной корреляционной матрицы получается 20 наборов матриц (смежности) разной степени разреженности.
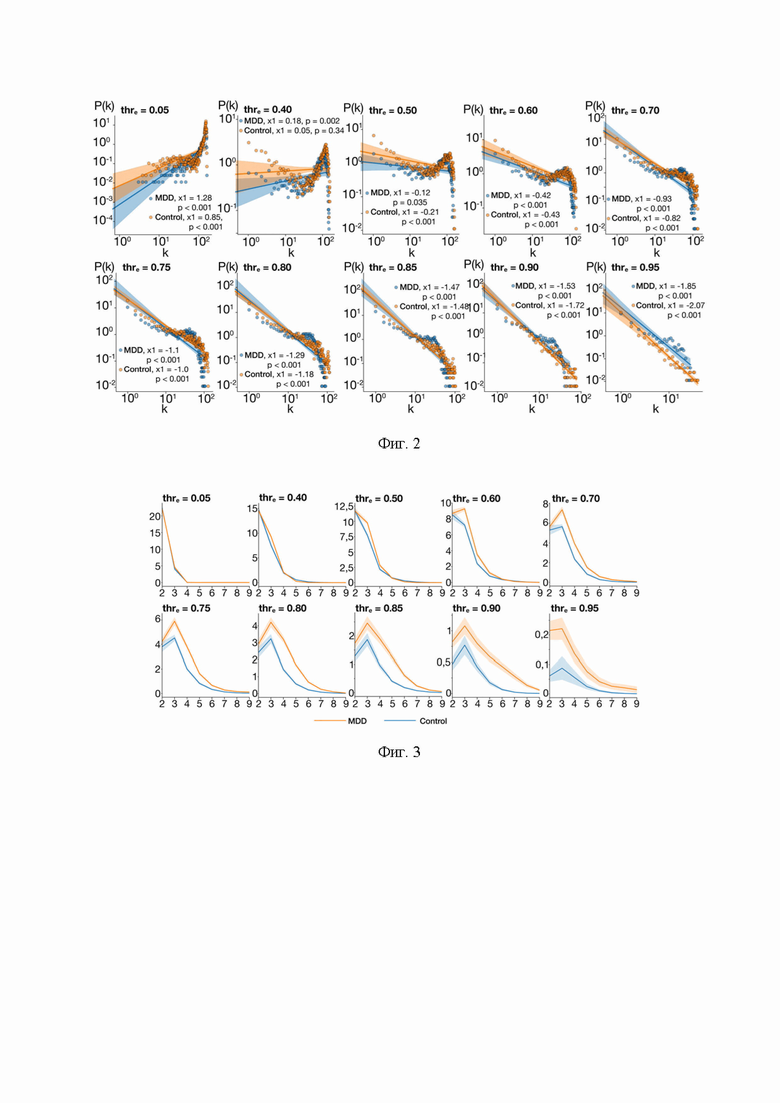
После применения порога производится анализ топологических свойств бинаризованных корреляционных матриц. Для каждого полученного набора матриц с характерным для него пороговым значением строят распределение относительных частот по значениям кратчайших путей графа для обеих групп испытуемых. Увеличение порогового значения приводит к изменению топологических характеристик анализируемых данных, переходя от распределения степеней, близкого к случайному, к безмасштабному распределению при максимальном пороге, как показано на фиг. 2. При этом вид распределения кратчайших путей меняется с увеличением порогового значения, и эти изменения различны в двух группах, как показано на фиг. 3. Для каждого распределения вычисляется значение d* - длина кратчайшего пути с максимальным значением t-статистики на основе t-критерия для независимых выборок с поправкой на задачу множественных сравнений. На фиг. 4(б) показана зависимость полученного значения t-статистики от применяемого порога 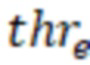 . Видно, что при увеличении порогового значения, количество кратчайших путей длины d значительно увеличивается в одной группе, но не в другой, при этом белая область, выделяющая значения t-статистики с соответствующим p < 0,05, соответствует более длинным кратчайшим путям с увеличением
. Видно, что при увеличении порогового значения, количество кратчайших путей длины d значительно увеличивается в одной группе, но не в другой, при этом белая область, выделяющая значения t-статистики с соответствующим p < 0,05, соответствует более длинным кратчайшим путям с увеличением 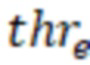 .
.
На третьем этапе осуществляется построение графового нейросетевого классификатора. Каждый набор данных, полученный с помощью применения пороговых значений 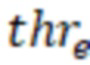 , используется для обучения трех моделей ГНС с количеством сверточных графовых слоев, равным d*, d*+1 и d*-1 для данной выборки с учетом возможной погрешности.
, используется для обучения трех моделей ГНС с количеством сверточных графовых слоев, равным d*, d*+1 и d*-1 для данной выборки с учетом возможной погрешности.
В данном изобретении используется ГНС со следующим набором гиперпараметров:
1) Скорость обучения (learning rate) - 0,0005;
2) Количество скрытых нейронов на всех слоях - 166;
3) Функция оптимизации - Adam;
4) Функция ошибки - бинарная кросс-энтропия;
5) Размер пакета - 32;
6) Исключение (dropout) - 20%;
7) Количество эпох обучения - 100.
Обязательными составляющими архитектуры ГНС являются один сверточный блок (GCN) и один выходной блок, содержание которых показано на фиг. 1(б). Сверточный блок состоит из оператора GraphConv:
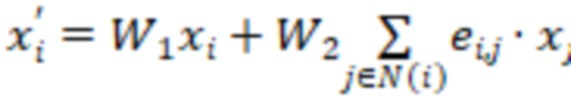 ,
,
где 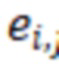 - вес ребра между узлами i и j [4].
- вес ребра между узлами i и j [4].
GCN блок также содержит функцию активации ReLU (rectified linear unit, линейный выпрямитель):
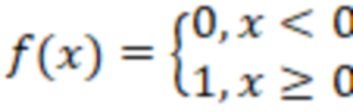 ,
,
и оператор пакетной нормализации (batch normalization).
Выходной блок (output block) содержит слой субдискретизации (global max pool) с функцией максимума для снижения размерности данных, полученных на предыдущем этапе в ходе обработки в блоке GCN, сигмоиду в качестве функции активации, оператор пакетной нормализации, оператор исключения с параметром 20% (dropout) и полносвязный линейный слой с 166 входными и одним выходным нейроном, который может находиться в состояниях «0» и «1», для финальной классификации двух целевых классов.
В процессе осуществления способа используется техника кросс-валидации на основе стратифицированного k-fold с количеством комбинаций, равным 10. Для оценки работы нейросетевого классификатора рассчитывается параметр F1-score, на основе которого принимается решение о качестве работы нейросетевого классификатора:
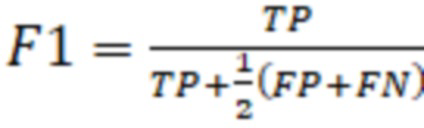 ,
,
где TP (true positive) - количество истинно-положительных решений (БДР есть, и оно обнаружено классификатором), FP (false positive) - количество ложноположительных решений (БДР отсутствует, но оно обнаружено) и FN (false negative) - количество ложноотрицательных решений (БДР есть, но оно не обнаружено). Метрика F1 имеет диапазон значений от 0 до 1, чем выше значение F1, тем выше качество классификации нейронной сети.
В результате в качестве графового нейросетевого классификатора выбирается модель с максимальным из трех построенных графовых нейронных сетей значением метрики F1. Данное решение основывается на том, что, как показано на фиг. 4(в), при увеличении порогового значения 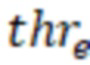 увеличивается также количество блоков GCN с максимальной оценкой F1 для данного набора данных. Помимо этого, на фиг. 4(г) показана стойкая корреляция между d* и параметром
увеличивается также количество блоков GCN с максимальной оценкой F1 для данного набора данных. Помимо этого, на фиг. 4(г) показана стойкая корреляция между d* и параметром 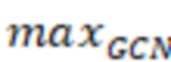 , равным количеству блоков GCN, показавшим наибольшую оценку F1 для данного набора данных (на фиг. 4(в) эти значения выделены белой рамкой). Видно, что между топологическими характеристиками исходного набора данных и «глубиной» архитектуры ГНС существует положительная корреляция с коэффициентом корреляции Спирмена 0,72 и соответствующим значением p < 0,05.
, равным количеству блоков GCN, показавшим наибольшую оценку F1 для данного набора данных (на фиг. 4(в) эти значения выделены белой рамкой). Видно, что между топологическими характеристиками исходного набора данных и «глубиной» архитектуры ГНС существует положительная корреляция с коэффициентом корреляции Спирмена 0,72 и соответствующим значением p < 0,05.
На фиг. 5 представлены ROC-кривые обучения, построенные на основе процесса обучения ГНС на корреляционных матрицах фМРТ для ГНС с одним блоком GCN (черная кривая) и ГНС с оптимальным количеством блоков GCN, выбранного на основе предлагаемого способа (красная кривая). Видно, что архитектура ГНС, подобранная индивидуально под каждый набор данных на основе топологических характеристик, показывает более стабильные результаты работы в сравнении со стандартной моделью с одним сверточным слоем.
На вход классификатора подают матрицу смежности испытуемого, для которого необходимо сделать вывод о наличии или отсутствии большого депрессивного расстройства: при получении на выходе классификатора значения «0» делают вывод об отсутствии у испытуемого большого депрессивного расстройства, при получении на выходе классификатора значения «1» делают вывод о наличии у испытуемого большого депрессивного расстройства.
Список источников
1. Venkatapathy S., Votinov M., Wagels L., Kim S., Lee M., Habel U., Ra I.H., Jo H.G. Ensemble graph neural network model for classification of major depressive disorder using whole-brain functional connectivity // Frontiers in Psychiatry. - 2023. - Vol. 14. 1125339.
2. Zhao, T., Zhang, G. Detecting Major Depressive Disorder by Graph Neural Network Exploiting Resting-State Functional MRI // In: Tanveer, M., Agarwal, S., Ozawa, S., Ekbal, A., Jatowt, A. (eds) Neural Information Processing. ICONIP 2022. Communications in Computer and Information Science. - 2023. - Springer, Singapore. - Vol. 1792.
3. Li Q., Han Z., Wu X.M. Deeper insights into graph convolutional networks for semi-supervised learning // Proceedings of the AAAI conference on artificial intelligence. - 2018. - Vol. 32. - №. 1.
4. Morris C. et al. Weisfeiler and leman go neural: Higher-order graph neural networks // Proceedings of the AAAI conference on artificial intelligence. - 2019. - Vol. 33. - №. 01. - P. 4602-4609.
Изобретение относится к способу графовой нейросетевой классификации на отсутствие или наличие большого депрессивного расстройства по данным фМРТ. Технический результат заключается в повышении точности определения наличия большого депрессивного расстройства по данным фМРТ. В способе регистрируют сигнал функциональной МРТ головного мозга в состоянии покоя у испытуемых контрольной группы и испытуемых с диагностированным большим депрессивным расстройством, в результате чего строят, в соответствии с автоматическим атласом анатомической разметки AAL3, корреляционную матрицу размером 166*166, каждый элемент корреляционной матрицы хранит в себе коэффициент корреляции Пирсона, к элементам матрицы применяют 20 пороговых значений в диапазоне от 0,0 до 0,95 с шагом 0,05, при этом значения коэффициента корреляции ниже порогового значения зануляют и из исходной матрицы получают 20 наборов матриц разной степени разреженности, бинаризуют матрицы путем присвоения значения «1» для коэффициентов корреляции, отличных от нуля, полученные 20 наборов бинаризованных матриц интерпретируют как матрицы смежности графов, для каждого набора с характерным для него пороговым значением строят распределение относительных частот по значениям кратчайших путей графа для обеих групп испытуемых, для каждого распределения вычисляют значение d* – длину кратчайшего пути с максимальным значением t-статистики на основе t-критерия для независимых выборок с поправкой на задачу множественных сравнений, строят и обучают на 20 наборах бинаризованных матриц разной степени разреженности, полученных на предыдущих этапах способа, три графовых нейронных сети с одним выходом, который может находиться в состояниях «0» и «1», и с количеством сверточных графовых слоев, равным соответственно d*, d*-1 и d*+1, рассчитывают значение метрики F1 для каждой из трех построенных графовых нейронных сетей, и в качестве классификатора выбирают сеть с максимальным из трех значением F1, подают на вход классификатора матрицу смежности испытуемого, для которого необходимо сделать вывод о наличии или отсутствии большого депрессивного расстройства: при получении на выходе классификатора значения «0» делают вывод об отсутствии у испытуемого большого депрессивного расстройства, при получении на выходе классификатора значения «1» делают вывод о наличии у испытуемого большого депрессивного расстройства. 5 ил.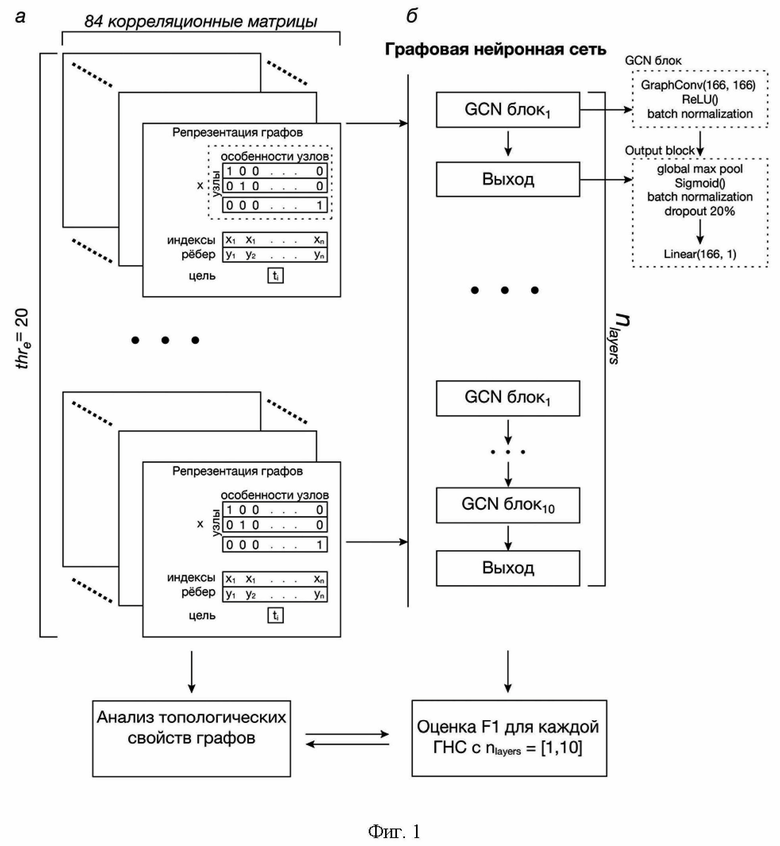
Способ графовой нейросетевой классификации на отсутствие или наличие большого депрессивного расстройства по данным фМРТ, при котором регистрируют сигнал функциональной МРТ головного мозга в состоянии покоя у испытуемых контрольной группы и испытуемых с диагностированным большим депрессивным расстройством, в результате чего строят, в соответствии с автоматическим атласом анатомической разметки AAL3, корреляционную матрицу размером 166*166, каждый элемент корреляционной матрицы хранит в себе коэффициент корреляции Пирсона, к элементам матрицы применяют 20 пороговых значений в диапазоне от 0,0 до 0,95 с шагом 0,05, при этом значения коэффициента корреляции ниже порогового значения зануляют и из исходной матрицы получают 20 наборов матриц разной степени разреженности, бинаризуют матрицы путем присвоения значения «1» для коэффициентов корреляции, отличных от нуля, полученные 20 наборов бинаризованных матриц интерпретируют как матрицы смежности графов, для каждого набора с характерным для него пороговым значением строят распределение относительных частот по значениям кратчайших путей графа для обеих групп испытуемых, для каждого распределения вычисляют значение d* – длину кратчайшего пути с максимальным значением t-статистики на основе t-критерия для независимых выборок с поправкой на задачу множественных сравнений, строят и обучают на 20 наборах бинаризованных матриц разной степени разреженности, полученных на предыдущих этапах способа, три графовых нейронных сети с одним выходом, который может находиться в состояниях «0» и «1», и с количеством сверточных графовых слоев, равным соответственно d*, d*-1 и d*+1, рассчитывают значение метрики F1 для каждой из трех построенных графовых нейронных сетей, и в качестве классификатора выбирают сеть с максимальным из трех значением F1, подают на вход классификатора матрицу смежности испытуемого, для которого необходимо сделать вывод о наличии или отсутствии большого депрессивного расстройства: при получении на выходе классификатора значения «0» делают вывод об отсутствии у испытуемого большого депрессивного расстройства, при получении на выходе классификатора значения «1» делают вывод о наличии у испытуемого большого депрессивного расстройства.
| Manyun Zhu и др | |||
| "The classification of brain network for major depressive disorder patients based on deep graph convolutional neural network", опубл | |||
| Прибор для получения стереоскопических впечатлений от двух изображений различного масштаба | 1917 |
|
SU26A1 |
| Elena Bondi и др | |||
| "A systematic review on the potential use of machine learning to classify major depressive | |||
Авторы
Даты
2024-05-17—Публикация
2023-06-16—Подача