Изобретение относится к измерительной и вычислительной технике и может быть использовано для автоматического контроля, поверки, исследования, метрологической оценки интегральной и дифференциальной нелинейностей аналого-цифровых преобразователей (АЦП) и получения информации об численных значениях погрешностях с представлением результатов в цифровой форме.
Известно устройство [1] для автоматического измерения характеристики преобразования быстродействующих АЦП, которое формирует с помощью аналогового интегратора измерительный сигнал с размахом в пределах одного кванта шкалы испытуемого АЦП. В связи с этим определяется напряжение, соответствующее среднему значению каждого кванта испытуемого АЦП. Однако, при автоматическом измерении характеристики преобразования прецизионных АЦП описанное выше условие задания измерительного сигнала невыполнимо, так как уже для 16-разрядного АЦП требования к точности задания параметров опорных сигналов становятся трудно выполнимыми.
Известно устройство [2] для автоматического измерения характеристики преобразования быстродействующих АЦП. Несмотря на то, что [2] является усовершенствованием известного устройства по авт. св. [1], за счет обеспечения одновременного автоматического измерения уровня случайных шумов АЦП в каждой измеряемой точке характеристики преобразования, его принцип работы также основан на прецизионных средствах измерений, что затрудняет использование данного устройства при испытаниях прецизионных АЦП.
Известно устройство [3] измерения характеристики преобразования высокоточных и быстродействующих АЦП. Указанное устройство также является усовершенствованием устройства по авт. св. [1], и имеет более высокую точность, которая определяется относительной погрешностью измерителя периодического временного интервала и цифрового интегрирующего вольтметра и составляет тысячные доли процента. Однако при измерении характеристики преобразования прецизионных АЦП описанное выше условие обеспечения требуемой точности невыполнимо, так как данное устройство сохраняет принцип работы, как и в вышеперечисленных устройствах, и не может быть использовано для определения интегральной и дифференциальной нелинейностей прецизионных АЦП.
Известно устройство [4] измерения характеристик АЦП с использованием цифро-аналогового преобразователя (ЦАП), которое позволяет определять реальную величину кванта, дифференциальную нелинейность и смещения уровней квантования. Это достигается за счет возможности независимого и одновременного определения смещений двух соседних реальных уровней квантования относительно номинального значения контролируемого кванта, путем формирования ЦАП сканирующего вспомогательного напряжения, размах которого перекрывает размах суммарной погрешности испытываемого АЦП. Однако использование указанного устройства для измерения характеристик прецизионных АЦП невозможно, так как принцип работы также основан на прецизионных средствах измерений.
Известно устройство [5] контроля АЦП с использованием генератора измерительного сигнала, которое позволяет проводить оценку значений характеристик по среднему значению реальных пороговых уровней преобразования. Несмотря на то, что [5] позволяет определить интегральную и дифференциальную статическую характеристику АЦП, его принцип работы также основан на прецизионных средствах измерений, где требования к точности задания параметров опорных сигналов для 24 разрядных АЦП на сегодняшний день реально не выполнимыми.
Наиболее близким к заявляемому является способ метрологического испытания и аттестации статических характеристик АЦП и устройство для его осуществления [6] с использованием генератора измерительного сигнала, управляемого аттенюатора, источника сигнала перемещения измерительного сигнала, схемы перемещения измерительного сигнала, микроконтроллера и ЭВМ, которое позволяет определять дифференциальную и интегральную нелинейность испытываемого АЦП путем перехода от прецизионных средств измерений к прецизионным методикам, при которых требования к образцовым средствам могут быть существенно снижены. Это достигается за счет смещения входного сигнала по всему динамическому диапазону АЦП, с номинальным шагом, соизмеримым с интервалом квантования АЦП. Однако способ требует больших временных затрат на проведение метрологического испытания, поскольку необходимо получить 2К (K - разрядность АЦП) локальных гистограмм для построения общей гистограммы. Кроме того, погрешность от нелинейности в [6] возникает в случае, когда имеются совместная нелинейность измерительного сигнала и интегральная нелинейность его перемещения.
Техническим результатом изобретения является возможность определения интегральной и дифференциальной нелинейностей АЦП, снизив требования к эталонным средствам измерений по классу точности за счет учета нелинейной составляющей измерительного сигнала (ИС). Это достигается за счет двух смещений входного сигнала, что значительно сокращает время проведения метрологического испытания.
Технический результат, реализуемый в способе определения интегральной и дифференциальной нелинейностей АЦП, достигается тем, что исходный измерительный сигнал (ИС) с входным диапазоном, равным входному диапазону испытываемого АЦП, подают на вход АЦП так, чтобы нижняя граница исходного ИС соответствовала минимальному напряжению кодового перехода АЦП и строят первую гистограмму распределения кодов АЦП, с помощью которой вычисляют время кодовых переходов АЦП, затем исходный ИС суммируют с сигналом перемещения, смещая исходный ИС по уровню вниз на величину, равную одной четверти входного диапазона АЦП, и строят вторую гистограмму распределения кодов АЦП, с помощью которой вычисляют время кодовых переходов АЦП при смещенном вниз ИС относительно исходного ИС, снова исходный ИС суммируют с сигналом перемещения, смещая исходный ИС по уровню вверх на величину, равную одной четверти входного диапазона АЦП, и строят третью гистограмму распределения кодов АЦП, с помощью которой вычисляют время кодовых переходов АЦП при смещенном вверх ИС относительно исходного ИС, после чего для каждого кода АЦП во второй и третьей гистограмме с помощью первой гистограммы составляют два уравнения, которые включают в себя интегральную нелинейность и время кодового перехода для текущего кода АЦП, количество интервалов квантований АЦП, нелинейную составляющую ИС и порядковый номер текущего кода АЦП, причем, одно из двух уравнений включает смещение ИС, далее два уравнения приводят к одному и решают полученные системы уравнений при смещении исходного ИС вниз и вверх методом наименьших квадратов, определяя смещение ИС и вклад нелинейной составляющей ИС в интегральную нелинейность для каждого кода АЦП во второй и третьей гистограмме, и учитывая нелинейную составляющую ИС, определяют интегральную нелинейность для каждого кода АЦП во второй и третьей гистограмме, объединяют интегральную нелинейность для кодов АЦП во второй гистограмме с интегральной нелинейностью для кодов АЦП в третьей гистограмме и получают интегральную нелинейность для каждого кода АЦП, за исключением минимального и максимального, а затем по интегральной нелинейности для каждого кода АЦП определяют дифференциальную нелинейность АЦП.
Для осуществления данного способа предлагаем устройство, содержащее генератор ИС, источник сигнала перемещения ИС, схему перемещения ИС, микроконтроллер и ЭВМ, причем первый вход схемы перемещения ИС соединен с выходом генератора ИС, а второй вход схемы перемещения ИС соединен с выходом источника сигнала перемещения ИС, управляющие входы генератора ИС и источника сигнала перемещения ИС соединены с первым и вторым выходами микроконтроллера, а выход схемы перемещения ИС соединен с входом испытываемого АЦП, выход которого соединен с входом микроконтроллера, третий выход которого связан через интерфейс с ЭВМ.
Суть способа определения интегральной и дифференциальной нелинейностей АЦП заключается в следующем. На вход испытываемого АЦП последовательно подают периодический ИС треугольной формы, смещенный по уровню вниз ИС и смещенный по уровню вверх ИС, и строят первую гистограмму распределения кодов АЦП при отсутствии смещения ИС, вторую и третью гистограммы при смещении ИС вниз и вверх, после чего для каждого кода АЦП во второй и третьей гистограмме с помощью первой гистограммы составляют два уравнения, которые приводят к одному и решают полученные системы уравнений при смещении ИС вниз и вверх методом наименьших квадратов, определяя смещение ИС и вклад нелинейной составляющей ИС в интегральную нелинейность для каждого кода АЦП во второй и третьей гистограмме, и учитывая нелинейную составляющую ИС, определяют интегральную нелинейность для каждого кода АЦП, а затем по интегральной нелинейности определяют дифференциальную нелинейность АЦП.
Для снятия трех гистограмм выполняют следующую последовательность действий.
1. Выделяют входной диапазон испытываемого АЦП: UH - нижнее напряжение АЦП, соответствующее минимальному напряжению кодового перехода испытываемого АЦП; UB - верхнее напряжение АЦП, соответствующее максимальному напряжению кодового перехода испытываемого АЦП.
2. Исходный периодический ИС треугольный формы с входным диапазоном, равным входному диапазону испытываемого АЦП, подают на вход АЦП так, чтобы нижняя граница исходного ИС соответствовала минимальному напряжению кодового перехода АЦП, и по количеству появлений каждого кода АЦП строят первую гистограмму.
3. Исходный ИС суммируют с сигналом перемещения, смещая исходный ИС по уровню вниз на величину, равную одной четверти входного диапазона АЦП, и по количеству появлений каждого кода АЦП строят вторую гистограмму.
4. Исходный ИС суммируют с сигналом перемещения, смещая исходный ИС по уровню вверх на величину, равную одной четверти входного диапазона АЦП, и по количеству появлений каждого кода АЦП строят третью гистограмму. На этом испытания заканчивают.
Покажем, как с помощью трех построенных гистограмм определяют вклад нелинейной составляющей ИС в интегральную нелинейность для каждого кода АЦП, за исключением минимального и максимального. Функцию преобразования (ФП) испытываемого АЦП с максимальным числом кодовых комбинаций N=2K в диапазоне от UH до UB можно представить следующим образом:
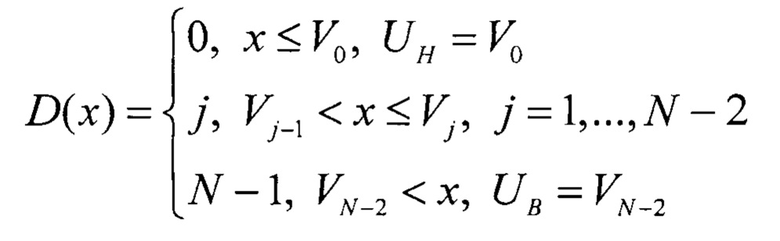
где D - выходной код АЦП;
x - входное аналоговое напряжение;
V0 - минимальное напряжение кодового перехода АЦП;
VN-2 - максимальное напряжение кодового перехода АЦП;
Vj - j-ое напряжение кодового перехода АЦП.
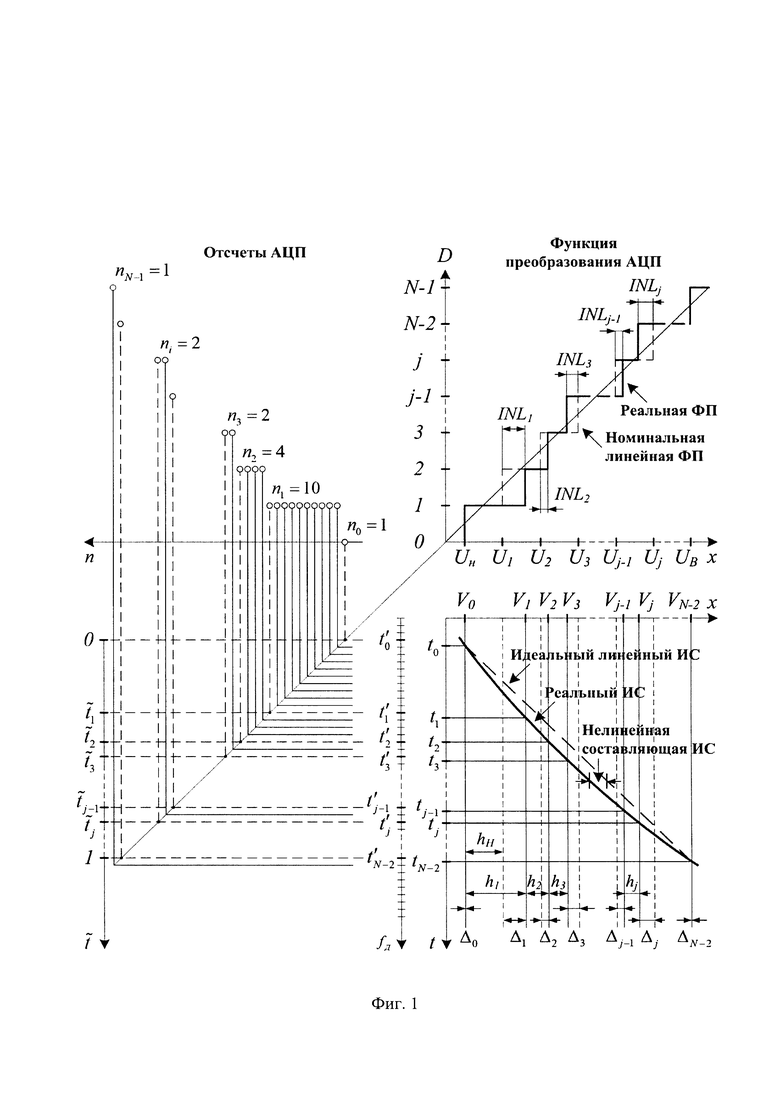
На фиг. 1 представлена реальная ФП с интегральной нелинейностью для каждого кода АЦП (INLj), за исключением минимального и максимального.
Идеальный АЦП с номинальной линейной ФП имеет равномерное распределение напряжений кодовых переходов Cj в диапазоне от UH до UB с постоянным приращением или шагом, называемым номинальным интервалом квантования hH, равным
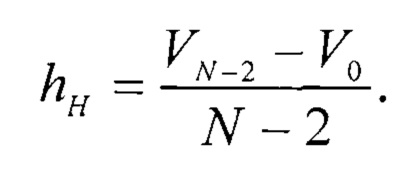
Напряжение кодового перехода идеального АЦП равно
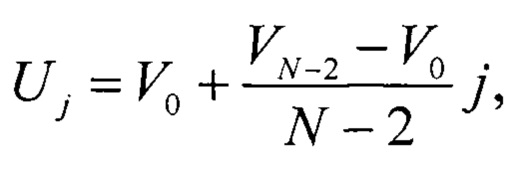
где j=0, 1, …, N-2 - порядковый номер текущего кода АЦП.
Интегральная нелинейность для j-го кода (или текущего кода) АЦП определяется как разность между реальным Vj и идеальным Uj напряжением кодового перехода АЦП
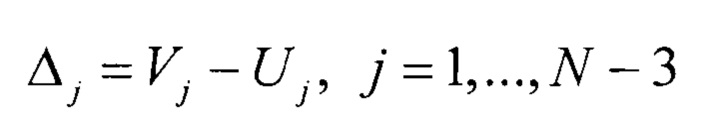
Выражая INLj относительно hH, получаем
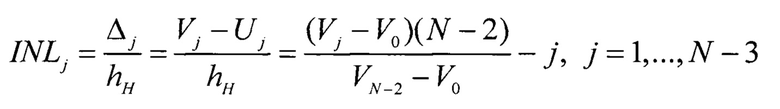
Интегральная нелинейность АЦП
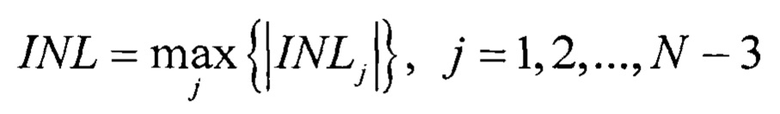
Дифференциальная нелинейность для j-го кода АЦП (DNLj) определяется как
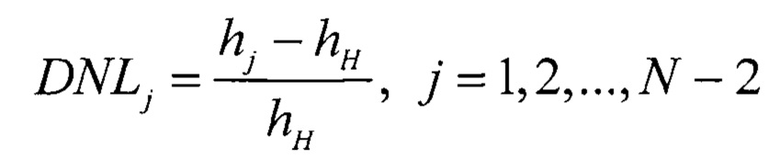
где hj - абсолютное значение j-го интервала квантования.
Так же с помощью INLj можно найти DNLj
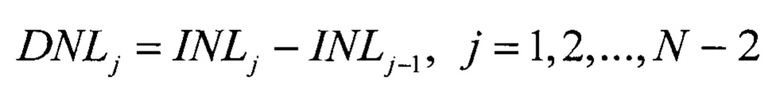
Известный гистограммный метод испытания АЦП [7] основан на формировании идеального линейного ИС, в то время как реальный ИС всегда имеет нелинейную составляющую, которая заставляет его отклоняться от прямой линии (фиг. 1).
Реальный ИС x(t) можно представить в виде
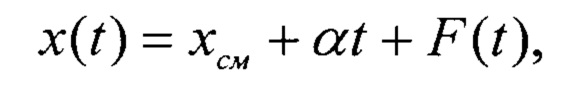
где хсм - напряжение смещения;
αt - линейная составляющая ИС;
F(t) - нелинейная составляющая ИС.
При подаче реального ИС x(t) на вход АЦП определить INLj не удается, так как любая нелинейность или искажения в ИС изменяют ожидаемое количество появлений кодов АЦП.
Введем понятие времени кодового перехода tj для j-го кода (или текущего кода) АЦП - это интервал времени, за который реальный ИС x(t) станет равным Vj и выходной код АЦП изменится с j на j+1. Условие равенства реального напряжения кодового перехода АЦП с реальным ИС x(t) выглядит следующим образом
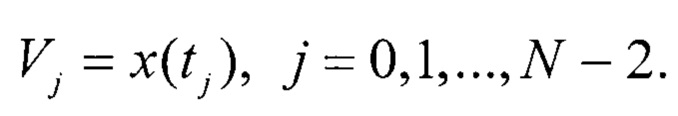
Пусть время кодового перехода для нижнего напряжения UH АЦП соответствует нулю (t0=0), а для верхнего напряжения UB АЦП соответствует единице (tN-2=1). Тогда напряжение смещения хсм реального ИС x(t) будет определяться минимальным напряжением кодового перехода АЦП (xсм=V0), а линейная составляющая ИС будет равна α=VN-2-V0. Нелинейная составляющая F(t) ИС при t0=0 и tN-2=1 будет равна нулю F(0)=F(1)=0.
Тогда, x(t) будет иметь вид
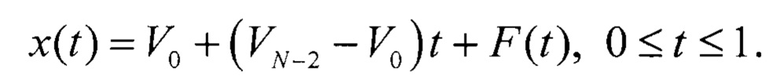
Данное выражение описывает реальный ИС, амплитуда которого равна UH при t0=0 и UB при tN-2=1, а нелинейность определяется F(t).
Представим F(t) с помощью набора базисных функций {Fi(t), i=1, 2, 3, …}. В качестве набора базисных функций используем тригонометрические функции на интервале [-1, 1].
Расширим F(t) для охвата интервала [-1, 1].
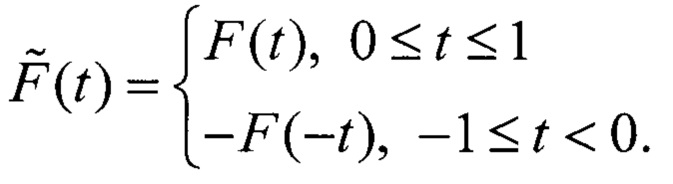
Представим 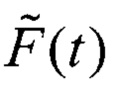 в виде тригонометрических функций
в виде тригонометрических функций
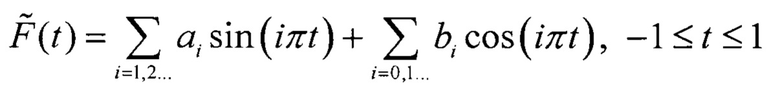
где ai, i=1, 2, … и bi, i=0, 1, 2, … - коэффициенты тригонометрических функций.
Поскольку расширенная функция нечетная, то коэффициенты функций косинуса равны нулю. Тогда, на интервале [0, 1] F(t) будет иметь вид:
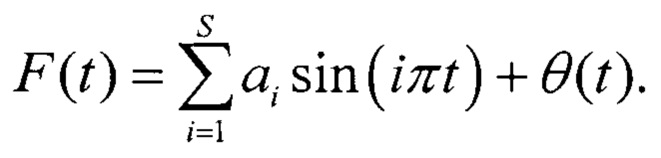
где θ(t) - остаток от нелинейности ИС, возникающий из-за ограниченного набора S базисными функциями.
Предлагаемый набор S может быть выбран таким, чтобы остаток от нелинейности ИС θ(t)→0. Выбор S зависит от скорости изменения нелинейной составляющей ИС. Нелинейность ИС может быть большой, но она не должна меняться слишком быстро для набора S≤10. В случае высокочастотной нелинейности необходимо увеличить набор базисных функций.
Считается, что функция F(t) определена, если определены коэффициенты ai, i=1, 2, …, S. Для упрощения вывода, в дальнейшем не будем использовать член θ(t).
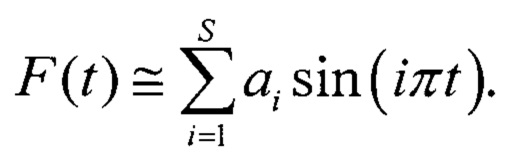
Другие варианты набора базисных функций {Fi(t), i=1, 2, 3, …} также могут быть использованы для описания F(t). Главное, чтобы все они удовлетворяли следующим условиям
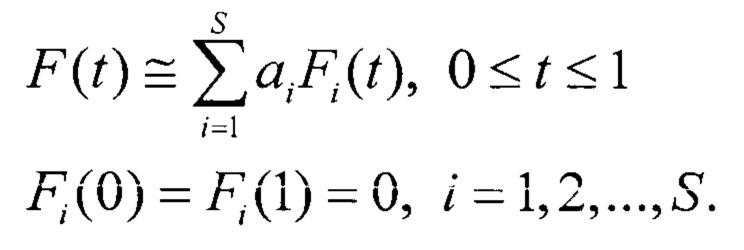
С учетом этого, выражение описывающее реальный ИС примет вид
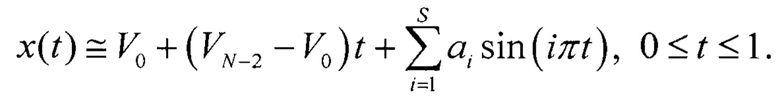
Для определения INLj представим напряжения кодовых переходов испытываемого АЦП через амплитудные значения реального ИС x(t), то есть
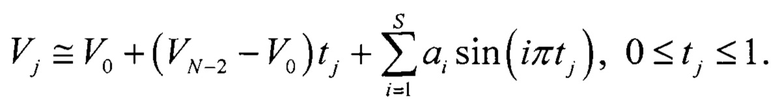
Тогда, интегральная нелинейность INLj для j-го кода АЦП равна
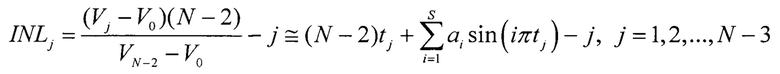
В полученном выражении коэффициенты ai представлены относительно hH.
Для вычисления tj используем гистограмму распределения кодов АЦП, где общее число отсчетов связано с частотой дискретизации fд АЦП. Так как период дискретизации АЦП является константой, то оценка времени кодового перехода 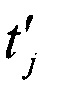 для j-го кода АЦП будет линейна пропорциональна числу отсчетов на интервале от t0=0 до tj. То есть, через количество появлений кодов АЦП ni можно оценить tj. Например (фиг. 1), n1=10 - количество появлений первого кода АЦП на интервале от t0=0 до t1, которое соответствует смене выходного кода АЦП с 1 на 2. Далее, n1+n2=14 - количество появлений первого и второго кода АЦП на интервале от t0=0 до t2, которое соответствует смене выходного кода АЦП с 2 на 3. Таким образом, n1+n2+…+ni - количество появлений кодов АЦП на интервале от t0=0 до tj, которое соответствует смене выходного кода АЦП с j на j+1, то есть
для j-го кода АЦП будет линейна пропорциональна числу отсчетов на интервале от t0=0 до tj. То есть, через количество появлений кодов АЦП ni можно оценить tj. Например (фиг. 1), n1=10 - количество появлений первого кода АЦП на интервале от t0=0 до t1, которое соответствует смене выходного кода АЦП с 1 на 2. Далее, n1+n2=14 - количество появлений первого и второго кода АЦП на интервале от t0=0 до t2, которое соответствует смене выходного кода АЦП с 2 на 3. Таким образом, n1+n2+…+ni - количество появлений кодов АЦП на интервале от t0=0 до tj, которое соответствует смене выходного кода АЦП с j на j+1, то есть
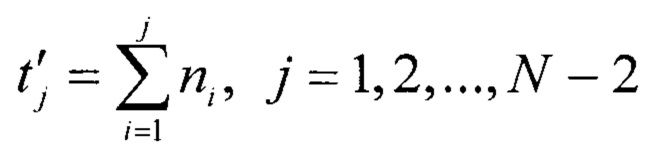
Поскольку выходной код АЦП меняется с N-2 на N-1 при tN-2=1, то общее количество появлений кодов АЦП на интервале от t0=0 до tN-2=1 определяется следующим образом
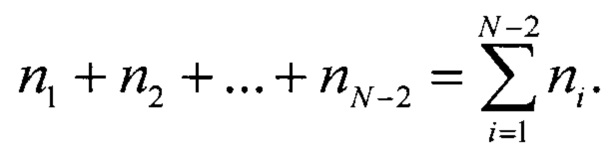
Сделаем рассматриваемый способ универсальным с помощью масштабного коэффициента 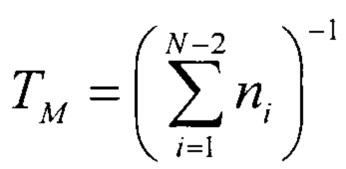 и перейдем от
и перейдем от 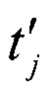 к нормированной оценки времени кодового перехода
к нормированной оценки времени кодового перехода 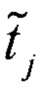 для j-го кода АЦП
для j-го кода АЦП
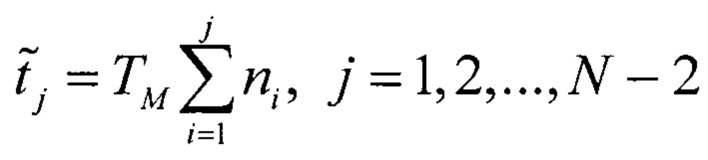
Условие смены выходного кода АЦП с j на j+1 можно представить как
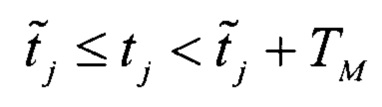
Поэтому оценка tj через количество появлений кодов АЦП ni имеет неопределенность, не более одного отсчета АЦП. Погрешность оценки tj может быть уменьшена, путем увеличения общего числа отсчетов в гистограмме.
Для этого на вход испытываемого АЦП, вместо ИС x(t), подают периодический ИС треугольный формы xT(t) в виде
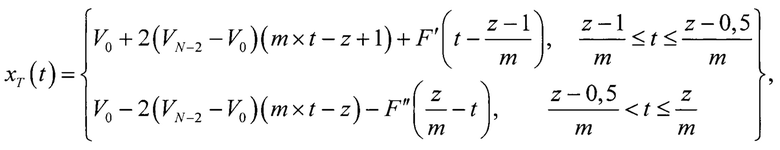
где m - число периодов ИС;
z - порядковый номер периода ИС;
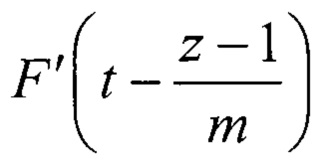 - нелинейная составляющая на возрастающем участке ИС;
- нелинейная составляющая на возрастающем участке ИС;
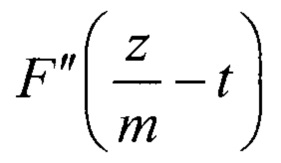 - нелинейная составляющая на убывающем участке ИС;
- нелинейная составляющая на убывающем участке ИС;
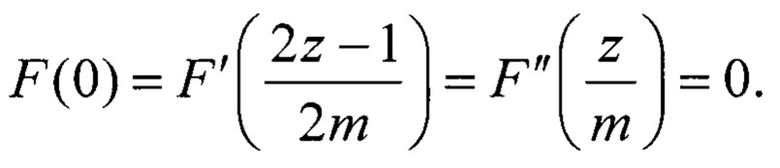
Итоговое выражение для оценки tj
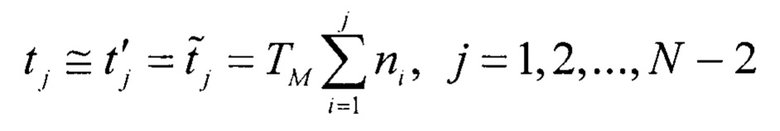
Данное выражение применимо для ИС x(t), так и для ИС xT(t), поэтому для упрощения вывода, в дальнейшем будет использовать ИС x(t) вида
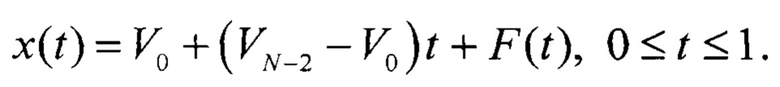
С учетом этого, оценка интегральной нелинейности 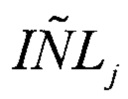 для j-го кода АЦП равна
для j-го кода АЦП равна
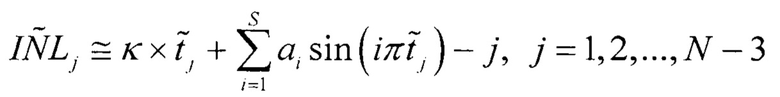
где κ=N-2 - количество интервалов квантований АЦП.
При линейном ИС коэффициенты ai равны нулю и для известного гистограммного метода испытания АЦП 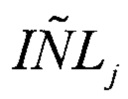 определяется как
определяется как
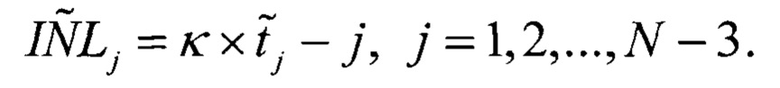
В случае реального ИС x(t) коэффициенты ai не равны нулю, в результате нелинейность АЦП и нелинейная составляющая F(t) ИС будут связаны друг с другом, и задача их одновременного определения не представляется выполнимой.
Поэтому на вход испытываемого АЦП последовательно подают ИС x1(t), смещенный по уровню вниз ИС x2(t) и смещенный по уровню вверх ИС x3(t):
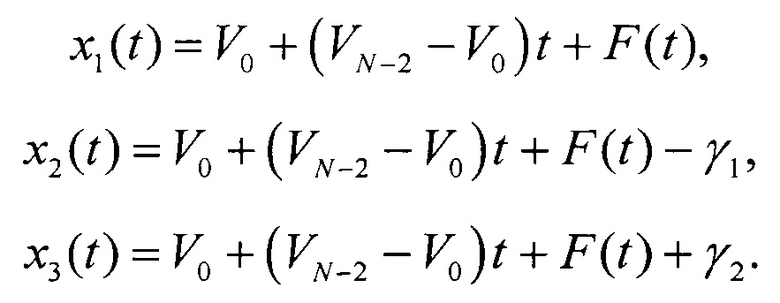
где у1 и у2 - напряжения смещений ИС.
Смещение исходного ИС x1(t) по уровню вниз и вверх позволяет найти коэффициенты ai и в итоге определить 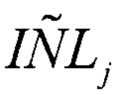 для каждого кода АЦП, за исключением минимального и максимального.
для каждого кода АЦП, за исключением минимального и максимального.
Измерительные сигналы х1(t), х2(t), х3(t) идентичны (линейные и нелинейные составляющие равны друг другу), за исключением неизвестного, но фиксированного напряжения смещения между ними. По этой причине время кодового перехода tj для одного и того же j-го кода АЦП, при отсутствии смещения ИС и
при смещении ИС вниз и вверх, будет отличаться друг от друга и поэтому обозначается по-разному.
Условие равенства реального напряжения кодового перехода АЦП с измерительными сигналами х1(t), x2(t), х3(t) выглядит следующим образом:
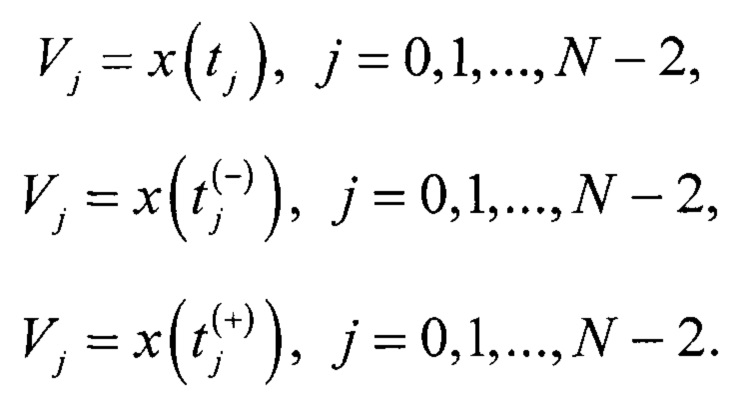
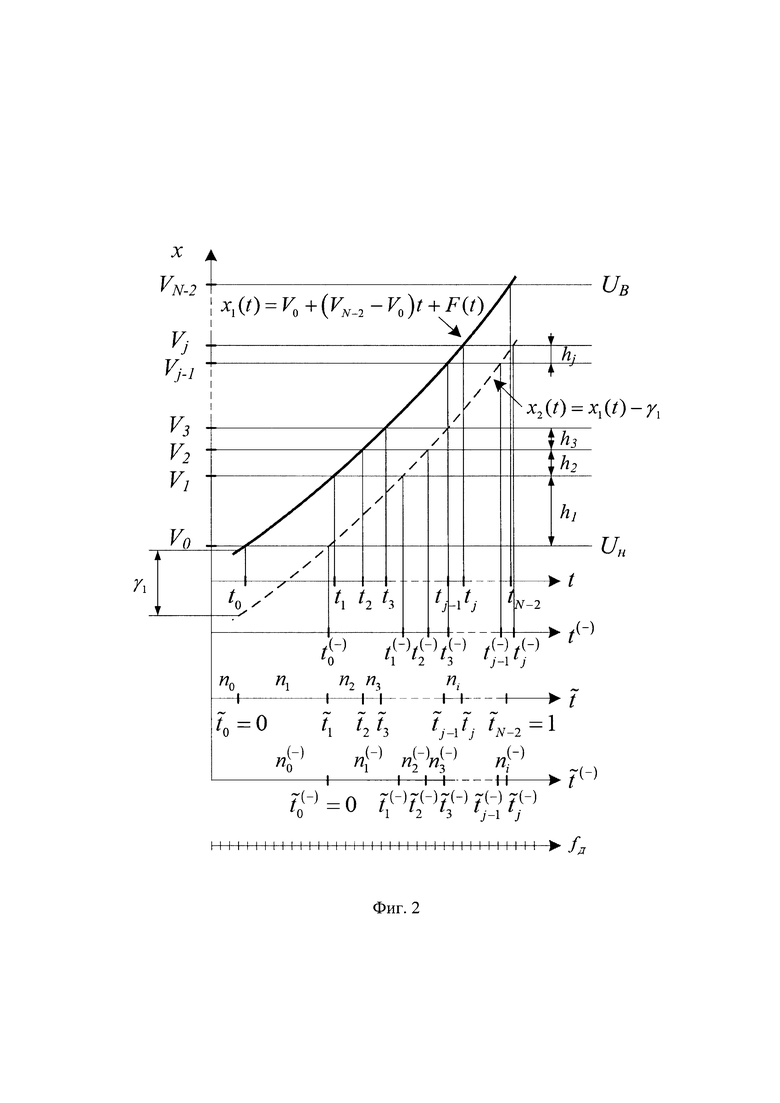
где 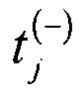 - время кодового перехода для j-го кода АЦП (фиг. 2), при смещенном вниз ИС х2(t) относительно исходного ИС х1(t);
- время кодового перехода для j-го кода АЦП (фиг. 2), при смещенном вниз ИС х2(t) относительно исходного ИС х1(t);
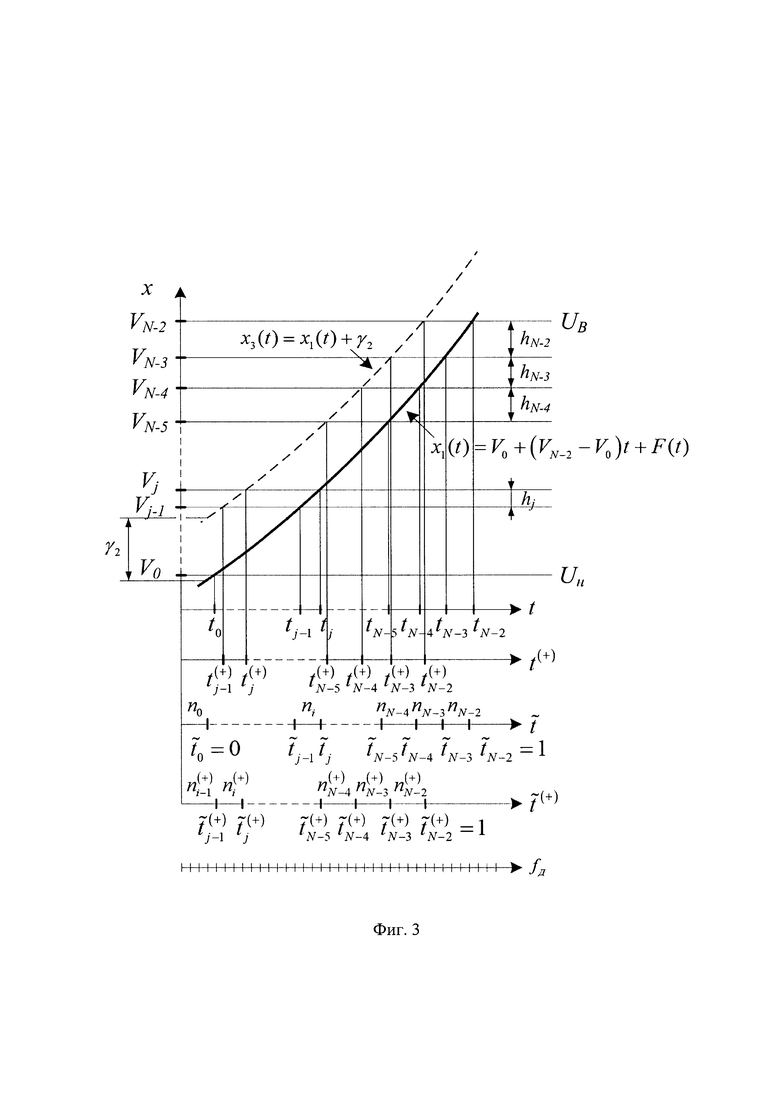
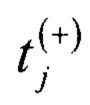 - время кодового перехода для j-го кода АЦП (фиг. 3), при смещенном вверх ИС х3(t) относительно исходного ИС х1(t).
- время кодового перехода для j-го кода АЦП (фиг. 3), при смещенном вверх ИС х3(t) относительно исходного ИС х1(t).
Смещенному вниз ИС х2(t) требуется больше времени по сравнению с исходным ИС х1(t) для достижения 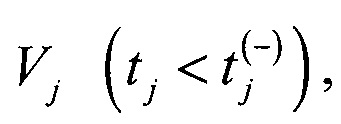 а смещенному вверх ИС х3(t) требуется меньше времени по сравнению с исходным ИС x1(t) для достижения Vj
а смещенному вверх ИС х3(t) требуется меньше времени по сравнению с исходным ИС x1(t) для достижения Vj 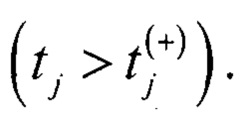
Строят первую гистограмму распределения кодов АЦП при отсутствии смещения ИС, вторую и третью гистограммы при смещении ИС вниз и вверх. С помощью первой гистограммы распределения кодов АЦП вычисляют 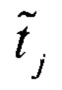
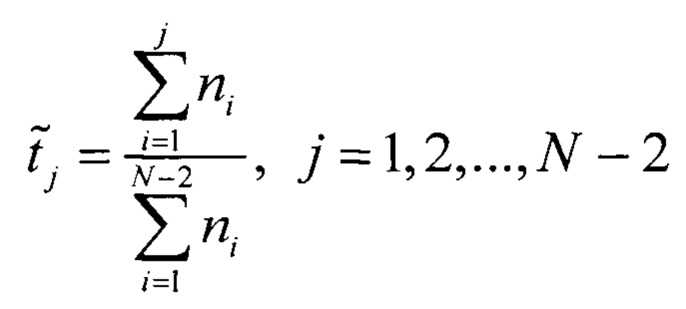
С помощью второй гистограммы распределения кодов АЦП вычисляют 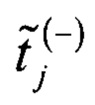
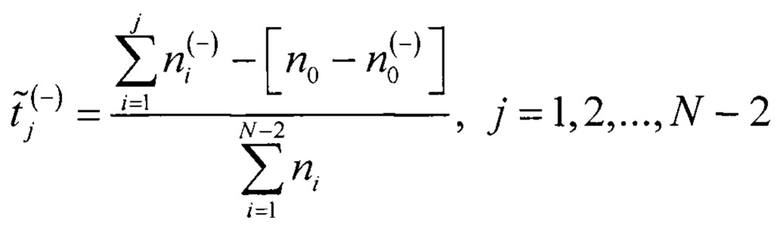
где 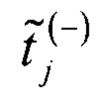 - нормированная оценка времени кодового перехода для j-го кода АЦП, при смещенном вниз ИС относительно исходного ИС;
- нормированная оценка времени кодового перехода для j-го кода АЦП, при смещенном вниз ИС относительно исходного ИС;
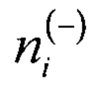 - количество появлений кодов АЦП по второй гистограмме;
- количество появлений кодов АЦП по второй гистограмме;
n0 - количество появлений кода из одних нулей (код 0) по первой гистограмме;
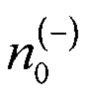 - количество появлений кода из одних нулей (код 0) по второй гистограмме;
- количество появлений кода из одних нулей (код 0) по второй гистограмме;
С помощью третьей гистограммы распределения кодов АЦП вычисляют 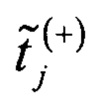
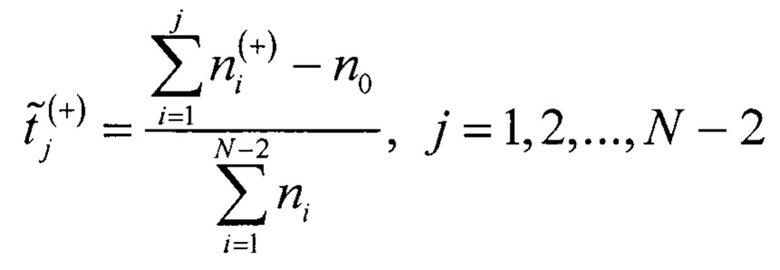
где 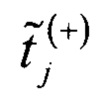 - нормированная оценка времени кодового перехода для j-го кода АЦП, при смещенном вверх ИС относительно исходного ИС;
- нормированная оценка времени кодового перехода для j-го кода АЦП, при смещенном вверх ИС относительно исходного ИС;
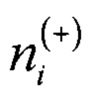 - количество появлений кодов АЦП по третьей гистограмме.
- количество появлений кодов АЦП по третьей гистограмме.
Покажем, почему одного смещения исходного ИС (вниз или вверх) не достаточно для определения вклада нелинейной составляющей ИС в интегральную нелинейность для каждого кода испытываемого АЦП.
1. Определение коэффициентов ai и интегральной нелинейности для j-го кода АЦП при смещении исходного ИС по уровню вниз.
Составляют первое уравнение для j-го кода АЦП:
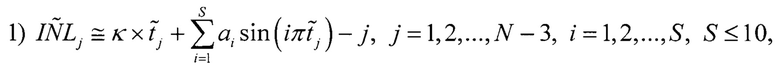
где 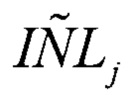 - оценка интегральной нелинейности для j-ого кода АЦП по первой гистограмме.
- оценка интегральной нелинейности для j-ого кода АЦП по первой гистограмме.
Составляют второе уравнение для j-го кода АЦП:
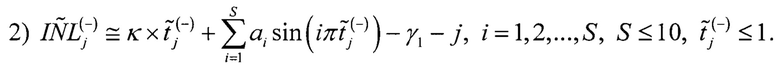
где 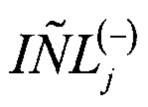 - оценка интегральной нелинейности для j-ого кода АЦП по второй гистограмме.
- оценка интегральной нелинейности для j-ого кода АЦП по второй гистограмме.
Поскольку составленные уравнения относятся к одному АЦП, то они равны при одном и том же индексе j. Поэтому два уравнения (1 и 2) приводят к одному, приравняв их правые части между собой, для исключения нелинейности АЦП
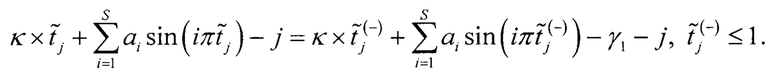
Переносят известные члены уравнения в левую часть, а все неизвестные в правую часть
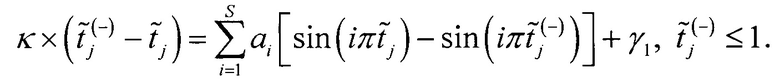
В итоге общее число уравнений будет значительно больше, чем число неизвестных ai и γ1. Например, у АЦП с разрешением более 10 бит всегда будет N>1000, в то время как число неизвестных не более 11. Поэтому неизвестные a1, …, aS и γ1 могут быть найдены с помощью метода наименьших квадратов.
Решение по методу наименьших квадратов для оценки неизвестных может быть представлено в следующем виде
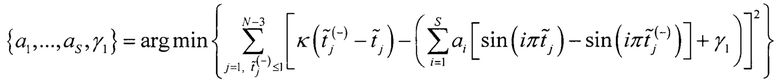
Учитывая γ1 и вклад нелинейной составляющей ИС (коэффициенты ai) в интегральную нелинейность для j-го кода АЦП определяют 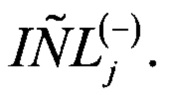
Значение напряжения смещения γ1 между x1(t) и х2(t) влияет на точность оценки 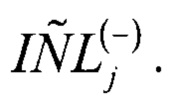 Чем меньше γ1, тем больше шум АЦП оказывает негативное влияние на точность определения неизвестных a1, …, aS. С другой стороны, чем больше γ1, тем больше участок амплитудного диапазона АЦП, в котором не удается учесть нелинейную составляющую ИС при определении
Чем меньше γ1, тем больше шум АЦП оказывает негативное влияние на точность определения неизвестных a1, …, aS. С другой стороны, чем больше γ1, тем больше участок амплитудного диапазона АЦП, в котором не удается учесть нелинейную составляющую ИС при определении 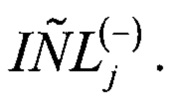
Для определения вклада нелинейной составляющей ИС в интегральную нелинейность для кодов АЦП в диапазоне от VN-2 - γ1 до VN-2 необходим ИС х3(t).
2. Определение коэффициентов ai и интегральной нелинейности для j-го кода АЦП при смещении исходного ИС по уровню вверх.
Составляют первое уравнение для j-го кода АЦП:
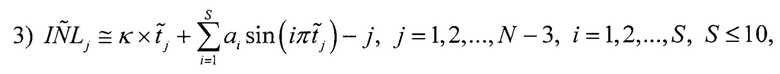
Составляют второе уравнение для j-го кода АЦП:
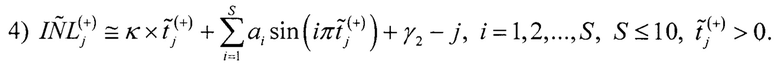
где 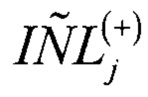 - оценка интегральной нелинейности для j-ого кода АЦП по третьей гистограмме.
- оценка интегральной нелинейности для j-ого кода АЦП по третьей гистограмме.
Уравнение 3 и 4 приводят к одному, приравняв их правые части между собой, для исключения нелинейности АЦП
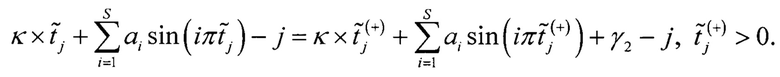
Переносят известные члены уравнения в левую часть, а все неизвестные в правую часть
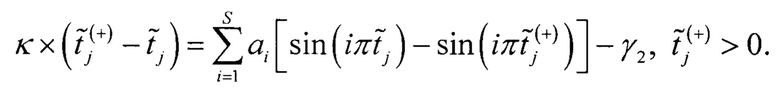
Находят неизвестные с помощью метода наименьших квадратов.
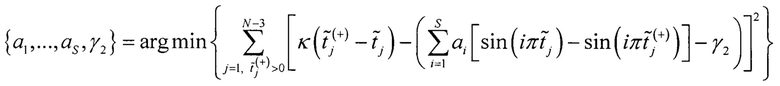
Учитывая γ2 и вклад нелинейной составляющей ИС (коэффициенты ai) в интегральную нелинейность для j-го кода АЦП определяют 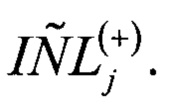
Объединяют 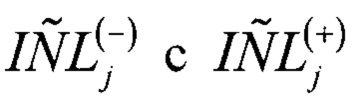 и получают оценку интегральной нелинейности для каждого кода АЦП
и получают оценку интегральной нелинейности для каждого кода АЦП 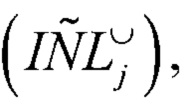 за исключением минимального и максимального.
за исключением минимального и максимального.
Определяют интегральную нелинейность АЦП
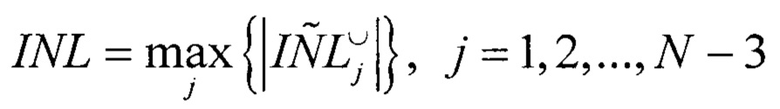
С помощью 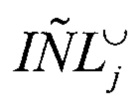 находят дифференциальную нелинейность АЦП
находят дифференциальную нелинейность АЦП
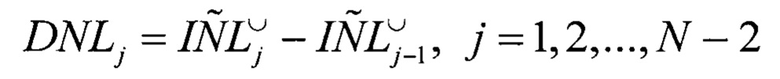
Кроме того, с помощью DNLj можно найти абсолютные значения интервалов квантований hj испытываемого АЦП следующим образом
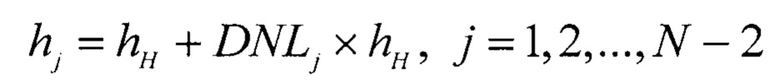
По зависимостям hj, DNLj, 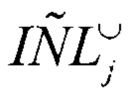 от текущего кода испытываемого АЦП можно определить предельные значения, средние значения, среднеквадратические отклонения дифференциальной и интегральной нелинейности, построить реальную ФП испытываемого АЦП.
от текущего кода испытываемого АЦП можно определить предельные значения, средние значения, среднеквадратические отклонения дифференциальной и интегральной нелинейности, построить реальную ФП испытываемого АЦП.
Нахождение напряжений смещений γ1 и γ2 является дополнительным преимуществом способа определения интегральной и дифференциальной нелинейностей АЦП, позволяющее снизить требования к точности задания сигнала перемещения.
Детальный анализ показал, что смещение исходного ИС по уровню вниз или вверх на величину, равную одной четверти входного диапазона АЦП подходит для предлагаемого способа. Смещение исходного ИС по уровню вниз или вверх на величину, более одной трети входного диапазона АЦП ведет к снижению точности определения коэффициентов ai и интегральной нелинейности АЦП.
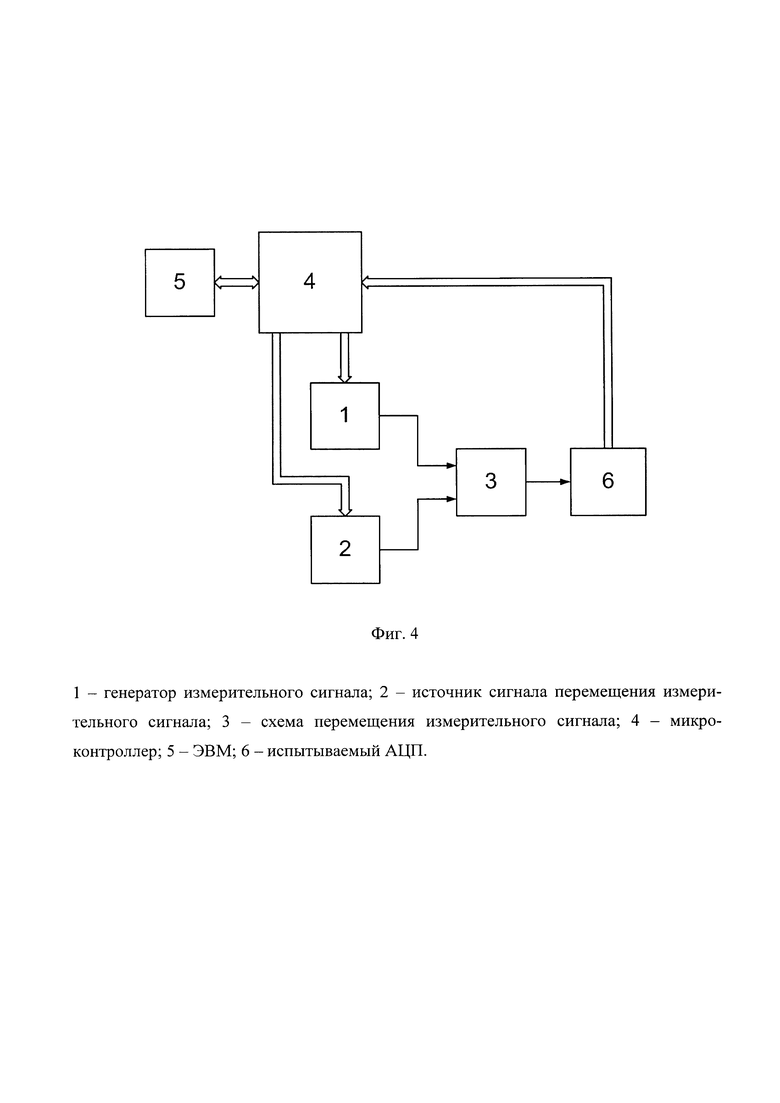
На фиг. 4 представлено устройство определения интегральной и дифференциальной нелинейностей АЦП.
Устройство содержит генератор ИС 1, источник сигнала перемещения ИС 2, схему перемещения ИС 3, микроконтроллер 4 и ЭВМ 5. При этом первый вход схемы перемещения ИС 3 соединен с выходом генератора ИС 1, а второй вход схемы перемещения ИС 3 соединен с выходом источника сигнала перемещения ИС 2. Управляющие входы генератора ИС 1 и источника сигнала перемещения ИС 2 соединены с первым и вторым выходами микроконтроллера 4. Выход схемы перемещения ИС 3 соединен с входом испытываемого АЦП 6, выход которого соединен с входом микроконтроллера 4, третий выход которого связан через интерфейс с ЭВМ 5.
Устройство работает следующим образом. Исходный ИС (периодическое напряжение треугольной формы) с входным диапазоном, равным входному диапазону испытываемого АЦП 6, сформированный с помощью генератора ИС 1, подают на первый вход схемы перемещения ИС 3. При этом исходный ИС с выхода схемы перемещения ИС 3 вначале формируют так, чтобы нижняя граница исходного ИС соответствовала минимальному напряжению кодового перехода АЦП 6 и фиксируют соответствующие коды с испытываемого АЦП 6 микроконтроллером 4, который в свою очередь передает эти коды на ЭВМ 6. Затем исходный ИС суммируют с сигналом перемещения, смещая исходный ИС по уровню вниз на величину, равную одной четверти входного диапазона испытываемого АЦП 6, подавая на второй вход схемы перемещения ИС 3 соответствующее напряжение с источника сигнала перемещения ИС 2 и фиксируют соответствующие коды с испытываемого АЦП 6 микроконтроллером 4, который в свою очередь передает эти коды на ЭВМ 5. Снова исходный ИС суммируют с сигналом перемещения, смещая исходный ИС по уровню вверх на величину, равную одной четверти входного диапазона испытываемого АЦП 6, подавая на второй вход схемы перемещения ИС 3 соответствующее напряжение с источника сигнала перемещения ИС 2 и фиксируют соответствующие коды с испытываемого АЦП 6 микроконтроллером 4, который в свою очередь передает эти коды на ЭВМ 5.
Таким образом, предложенный способ и устройство для его осуществления позволяют определять интегральную и дифференциальную нелинейности АЦП, снизив требования к эталонным средствам измерений по классу точности за счет учета нелинейной составляющей измерительного сигнала.
Литература
1. Патент SU 1058048 А1, МПК Н03К 13/02, 1983
2. Патент SU 1181136 А2, МПК Н03М 1/10, 1985
3. Патент SU 1211879 А1, МПК Н03М 1/10, 1986
4. Патент SU 1282324 А1, МПК Н03М 1/10, 1987
5. Патент SU 1287285 А1, МПК Н03М 1/10, 1987
6. Патент RU 2337475 С1, МПК Н03М 1/10, 2008
7. Аналого-цифровое преобразование / под ред. У. Кестера. - М.: Техносфера, 2007. - 1016 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МЕТРОЛОГИЧЕСКОГО ИСПЫТАНИЯ И АТТЕСТАЦИИ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК АЦП И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2007 |
|
RU2337475C1 |
| АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ И СПОСОБ ЕГО КАЛИБРОВКИ | 2010 |
|
RU2442279C1 |
| Устройство для первичной обработки сейсмической информации | 1981 |
|
SU1057958A1 |
| ТЕЛЕМЕТРИЧЕСКИЙ РЕГИСТРАТОР БИОПОТЕНЦИАЛОВ С ГИБКОЙ МАРКИРУЕМОЙ КОМПЕНСАЦИЕЙ ДРЕЙФА ИЗОЛИНИИ | 2002 |
|
RU2220654C2 |
| КОНТЕНТ-АДАПТИВНЫЙ ПЕРЦЕПЦИОННЫЙ КВАНТИЗАТОР ДЛЯ ИЗОБРАЖЕНИЙ С ВЫСОКИМ ДИНАМИЧЕСКИМ ДИАПАЗОНОМ | 2016 |
|
RU2678483C1 |
| СПОСОБ ТЕРМОСТАБИЛИЗАЦИИ АКТИВНОЙ ИНДУКТИВНОСТИ | 1990 |
|
RU2017326C1 |
| ЦИФРОВАЯ АВТОМАТИЗИРОВАННАЯ СХЕМА ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ И ТЕПЛОВОЙ КАЛИБРОВКИ КАЛОРИМЕТРА ПЕРЕМЕННОЙ ТЕМПЕРАТУРЫ | 2008 |
|
RU2377512C1 |
| ЦИФРОВОЙ ИЗМЕРИТЕЛЬ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК | 2012 |
|
RU2520956C2 |
| Измеритель параметров комплексных сопротивлений | 1989 |
|
SU1751690A1 |
| СПОСОБ ДЛЯ ЦИФРОВОЙ СУБСТРАКЦИОННОЙ АНГИОГРАФИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1992 |
|
RU2043073C1 |
Изобретение относится к области измерительной и вычислительной техники, а именно к метрологическим испытаниям аналого-цифровых преобразователей (АЦП). Техническим результатом является возможность определения интегральной и дифференциальной нелинейностей АЦП, снизив требования к эталонным средствам измерений по классу точности за счет учета нелинейной составляющей измерительного сигнала (ИС). Для этого устройство определения интегральной и дифференциальной нелинейностей АЦП содержит генератор ИС, источник сигнала перемещения ИС, схему перемещения ИС, микроконтроллер и ЭВМ. При этом первый вход схемы перемещения ИС соединен с выходом генератора ИС, а второй вход схемы перемещения ИС соединен с выходом источника сигнала перемещения ИС. Управляющие входы генератора ИС и источника сигнала перемещения ИС соединены с первым и вторым выходами микроконтроллера. Выход схемы перемещения ИС соединен с входом испытываемого АЦП, выход которого соединен с входом микроконтроллера, третий выход которого связан через интерфейс с ЭВМ. 2 н.п. ф-лы, 4 ил.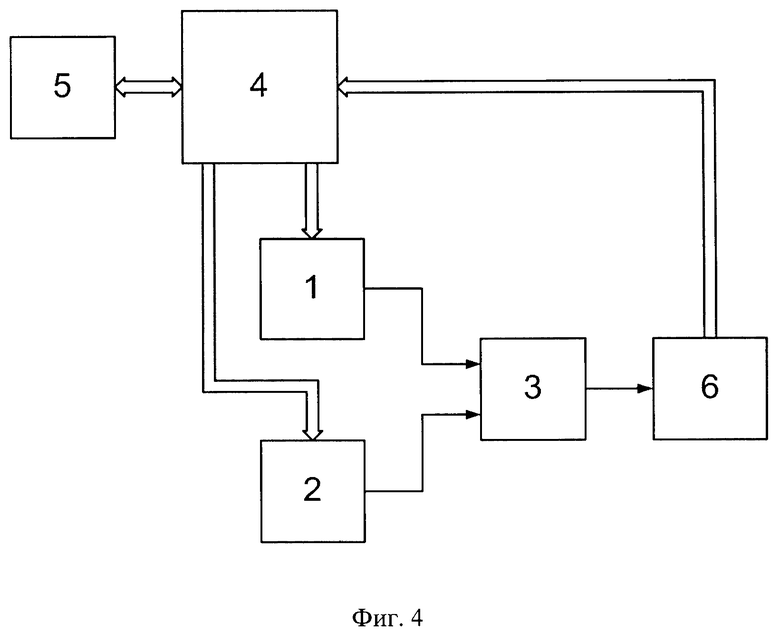
1. Способ определения интегральной и дифференциальной нелинейностей аналого-цифровых преобразователей (АЦП), заключающийся в формировании измерительного сигнала и сигнала перемещения, отличающийся тем, что исходный измерительный сигнал (ИС) с входным диапазоном, равным входному диапазону испытываемого АЦП, подают на вход АЦП так, чтобы нижняя граница исходного ИС соответствовала минимальному напряжению кодового перехода АЦП и строят первую гистограмму распределения кодов АЦП, с помощью которой вычисляют время кодовых переходов АЦП, затем исходный ИС суммируют с сигналом перемещения, смещая исходный ИС по уровню вниз на величину, равную одной четверти входного диапазона АЦП, и строят вторую гистограмму распределения кодов АЦП, с помощью которой вычисляют время кодовых переходов АЦП при смещенном вниз ИС относительно исходного ИС, снова исходный ИС суммируют с сигналом перемещения, смещая исходный ИС по уровню вверх на величину, равную одной четверти входного диапазона АЦП, и строят третью гистограмму распределения кодов АЦП, с помощью которой вычисляют время кодовых переходов АЦП при смещенном вверх ИС относительно исходного ИС, после чего для каждого кода АЦП во второй и третьей гистограмме с помощью первой гистограммы составляют два уравнения, которые включают в себя интегральную нелинейность и время кодового перехода для текущего кода АЦП, количество интервалов квантований АЦП, нелинейную составляющую ИС и порядковый номер текущего кода АЦП, причем одно из двух уравнений включает смещение ИС, далее два уравнения приводят к одному и решают полученные системы уравнений при смещении исходного ИС вниз и вверх методом наименьших квадратов, определяя смещение ИС и вклад нелинейной составляющей ИС в интегральную нелинейность для каждого кода АЦП во второй и третьей гистограмме и учитывая нелинейную составляющую ИС, определяют интегральную нелинейность для каждого кода АЦП во второй и третьей гистограмме, объединяют интегральную нелинейность для кодов АЦП во второй гистограмме с интегральной нелинейностью для кодов АЦП в третьей гистограмме и получают интегральную нелинейность для каждого кода АЦП, за исключением минимального и максимального, а затем по интегральной нелинейности для каждого кода АЦП определяют дифференциальную нелинейность АЦП.
2. Устройство определения интегральной и дифференциальной нелинейностей АЦП, содержащее генератор измерительного сигнала (ИС), источник сигнала перемещения ИС, схему перемещения ИС, микроконтроллер и ЭВМ, отличающееся тем, что первый вход схемы перемещения ИС соединен с выходом генератора ИС, а второй вход схемы перемещения ИС соединен с выходом источника сигнала перемещения ИС, управляющие входы генератора ИС и источника сигнала перемещения ИС соединены с первым и вторым выходами микроконтроллера, а выход схемы перемещения ИС соединен с входом испытываемого АЦП, выход которого соединен с входом микроконтроллера, третий выход которого связан через интерфейс с ЭВМ, причем схема перемещения ИС выполнена с возможностью, чтобы исходный ИС с выхода схемы перемещения ИС вначале формировался так, чтобы нижняя граница исходного ИС соответствовала минимальному напряжению кодового перехода АЦП, в результате чего микроконтроллер фиксирует соответствующие коды с испытываемого АЦП и передает эти коды на ЭВМ для определения первой гистограммы распределения кодов АЦП, с помощью которой вычисляют время кодовых переходов АЦП, затем схема перемещения ИС суммирует исходный ИС с сигналом перемещения, смещая исходный ИС по уровню вниз на величину, равную одной четверти входного диапазона АЦП, при этом ЭВМ определяет вторую гистограмму распределения кодов АЦП, с помощью которой вычисляют время кодовых переходов АЦП при смещенном вниз ИС относительно исходного ИС, далее схема перемещения ИС суммирует исходный ИС с сигналом перемещения, смещая исходный ИС по уровню вверх на величину, равную одной четверти входного диапазона АЦП, и ЭВМ определяет третью гистограмму распределения кодов АЦП, с помощью которой вычисляют время кодовых переходов АЦП при смещенном вверх ИС относительно исходного ИС, далее ЭВМ определяет интегральную нелинейность для каждого кода АЦП во второй и третьей гистограмме, объединяет интегральную нелинейность для кодов АЦП во второй гистограмме с интегральной нелинейностью для кодов АЦП в третьей гистограмме и получает интегральную нелинейность для каждого кода АЦП, за исключением минимального и максимального, а затем по интегральной нелинейности для каждого кода АЦП определяет дифференциальную нелинейность АЦП.
| СПОСОБ МЕТРОЛОГИЧЕСКОГО ИСПЫТАНИЯ И АТТЕСТАЦИИ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК АЦП И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2007 |
|
RU2337475C1 |
| Способ изготовления цветных кинематографических лент | 1932 |
|
SU44436A1 |
| СПОСОБ КОРРЕКЦИИ ПОГРЕШНОСТЕЙ АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАНИЯ | 1993 |
|
RU2085033C1 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
Авторы
Даты
2024-10-18—Публикация
2024-02-07—Подача