Изобретение относится к области вычислительной техники и может быть использовано в цифровых вычислительных устройствах, а также в устройствах для формирования элементов конечных полей.
Известен умножитель по модулю (патент RU 2299461 С1, МПК G06F 7/523, G06F 7/72, 2007), который содержит умножитель, n сумматоров, n инверторов, (n-1) умножителей на константу, где n- размер умножителя, мультиплексор, два выхода для подачи двоичных кодов умножаемых чисел, вход для подачи двоичного кода модуля p, выход.
Недостатком данного устройства являются значительные схемные (аппаратные) затраты на его реализацию.
Основной задачей является снижение аппаратных затрат на выполнение операции умножения по модулю.
Техническим результатом, достигнутым при осуществлении заявленного изобретения, является снижение аппаратных затрат на реализацию умножителя по модулю.
Указанный технический результат достигается за счет введения 16 двухвходовых элементов И, 6 двухвходовых сумматоров по модулю два, 4 многовходовых сумматоров по модулю два.
При проведении умножения по модулю p(z)=z4+z+1, двух операндов A(z) и B(z), степени которых удовлетворяют условию:

Могут быть получены результаты, которые являются элементами поля Галуа GF(24). В таблице 1 приведены ненулевые элементы поля GF(24), порождаемые неприводимым полиномом p(z)=z4+z+1.
Таблица 1
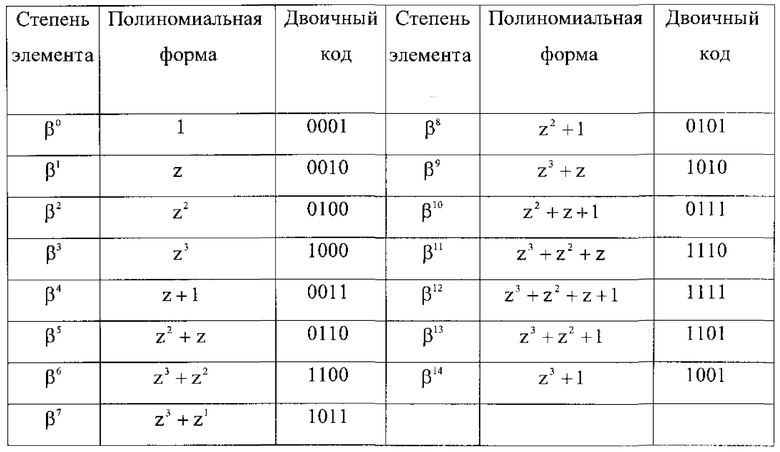
Так как операнды А и В представляют собой четырехразрядные комбинации, то максимальная степень их полиномиальной формы записи будет равна трем. Поэтому необходимо определить результаты каждого разряда первого операнда A(z) на каждый разряд операнда B(z).
Пусть A{z)=1. Тогда результаты умножения A(z)B(z) по модулю p(z)=z4+z+1 приведены в таблице 2.
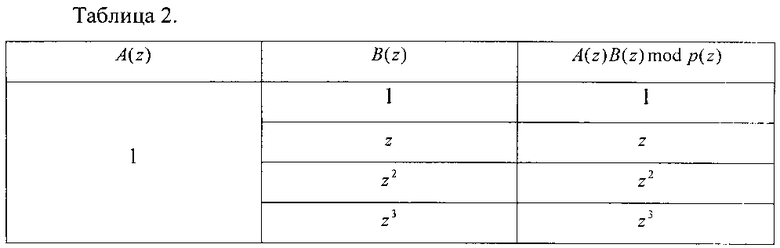
Пусть A(z)=z. Тогда результаты умножения приведены в таблице 3.
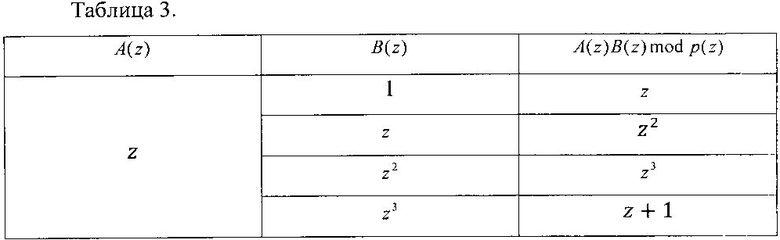
Пусть A(z)=z2. Тогда результаты умножения приведены в таблице 4.
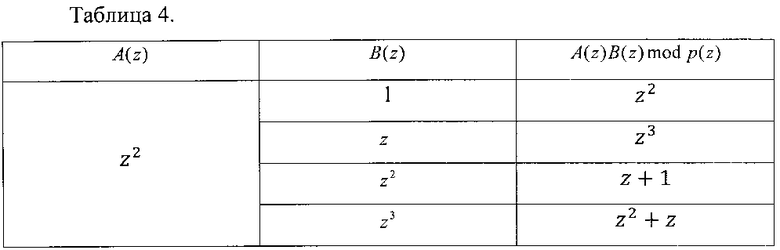
Пусть A{z)=z3. Тогда результаты умножения приведены в таблице 5.
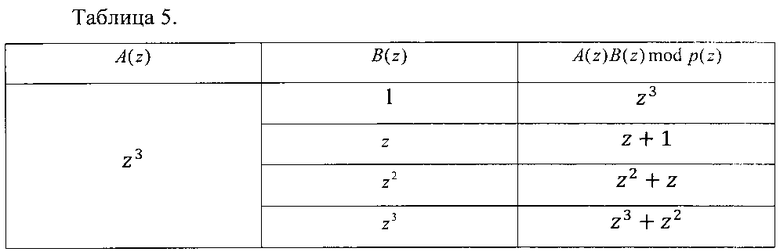
Обобщая данные, приведенные в таблицах 2-5, можно определить, какие разряды операндов A(z) и B(z) участвуют в получении каждого разряда произведения A(z)B(z) mod p(z). Результаты приведены в таблице 6.
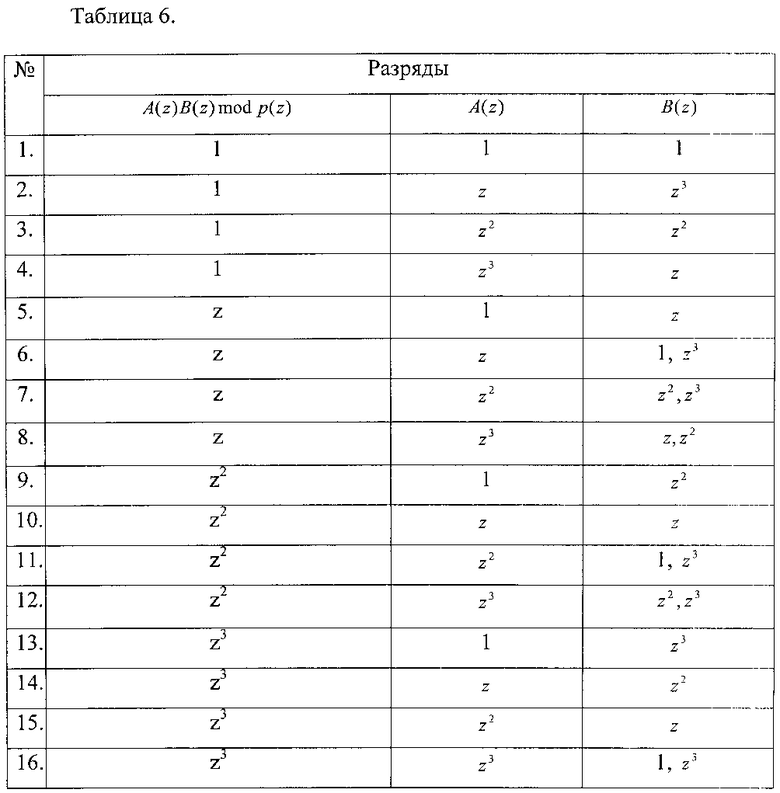
Рассмотрим первую строку данной таблицы. Для того чтобы получить произведение A(z)B(z) mod p(z)=1, при условии, что операнд A(z)=1, необходимо условие, что B(z)=1. Таким образом, для выполнения операции умножения по модулю для данных разрядов операндов достаточно использовать двухвходовой элемент И. Аналогичный результат получается для строки 2, 3, 4, 5, 9, 10, 13, 14, 15 таблицы 6.
Рассмотрим шестую строку таблицы 6. Для того чтобы получить значения произведения A(z)B(z)modp(z)=z при условии, что первый операнд A(z)=z, значение второго операнда A(z)=z может быть 1 или z. Это обусловлено равенствами
z·1modz4+z+1=z,
z·z3 modz4+z+1=z4 mod z4+z+1=z+1,
в произведениях которых присутствует значение z.
Если одновременно подать единичный сигнал на разряды 1 и z3 второго операнда B(z), при условии, что A(z)=z, то получаем результат:
A(z)B(z)modz4+z+1=(z(z3+1))modz4+z+1=(z4+z)modz4+z+1=1.
Данный результат можно получить, если сложить результаты двух произведений по модулю два:
(z·1)modz4+z+1+(z-z3)modz4+z+1=z+z+1=1.
Значит, чтобы решить данную проблему, необходимо использовать двухвходовой сумматор по модулю два, на входы которого подаются сигналы с 1 и z3 второго операнда B(z). Выход этого сумматора по модулю два подключается на второй вход элемента И, на первый вход которого поступает сигнал в разряде z первого операнда A(z). Аналогичный результат получается для строк 6, 7, 8, 11, 12, 16 таблицы 6.
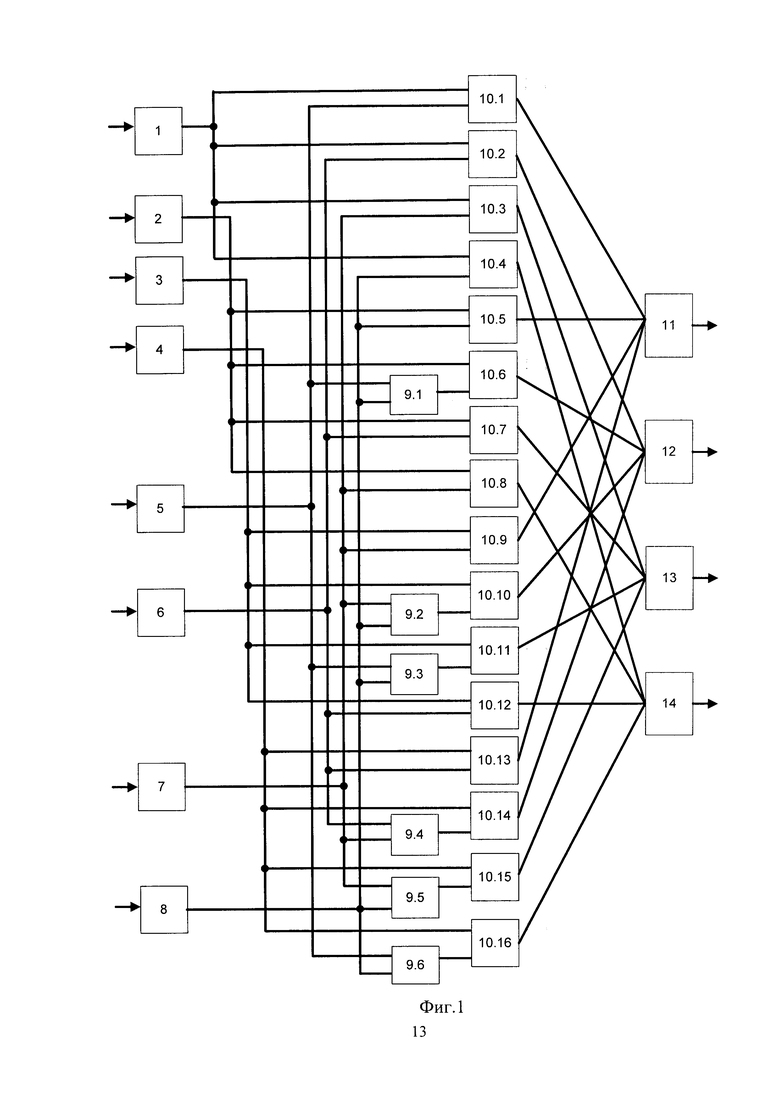
На фигуре 1 приведена структура умножителя по модулю. Он содержит входы 1-4, на которые поступает в двоичном коде первый операнд A(z), входы 5-8, на которые подается двоичный код второго операнда B{z), блок двухвходовых сумматоров по модулю два 9.1-9.6, блок двухвходовых элементов И 10.1-10.16, сумматоры по модулю два 11-14, выходы которых являются выходом умножителя по модулю. При этом младшие разряды «1» первого и второго операндов A(z) и B(z) поступают на входы 1 и 5 соответственно, а старший разряд z3 - соответственно на входы 4 и 8. Первый вход 1 первого операнда A(z) подключен к первым выходам элементов И 10.1-10.4. Второй вход 2 первого операнда A(z) подключен к первым входам элементов И 10.5-10.8. Третий вход, по которому передается разряд z2 первого операнда A(z), подключен к первым входам элементов И 10.9-10.12. Четвертый вход 4 умножителя по модулю, по которому передается разряд z3 первого операнда A(z), подключен к первым входам элементов И 10.13-10.16. Пятый вход 5 умножителя по модулю, по которому подается разряд 1 второго операнда B(z), подключен ко второму входу элемента И 10.1, а также к первым входам сумматоров по модулю два 9.1, 9.3, 9.6. Шестой вход 6 умножителя по модулю, по которому подается разряд z второго операнда B(z), подключен ко вторым входам элементов И 10.2, 10.7, 10.12, 10.13 и первому входу сумматора по модулю два 9.4. Седьмой вход умножителя по модулю, по которому подается разряд z2 второго операнда B(z), подключен ко второму входу элементов И 10.3, 10.8, 10.9 и первому входу сумматоров по модулю два 9.2 и 9.5, а также второму входу сумматора по модулю два 9.4. Восьмой вход 8 умножителя по модулю, по которому подается разряд z3 второго операнда B(z), подключен ко второму входу элементов И 10.4, 10.5 и второму входу сумматоров по модулю два 9.1, 9.2, 9.3, 9.5, 9.6. Выходы сумматоров по модулю два 9.1- 9.6 подключены ко вторым входам элементов И 10.6, 10.10, 10.11, 10.14, 10.15, 10.16 соответственно. Входы сумматора по модулю два 11 соединены с выходами элементов И 10.1, 10.5, 10.9, 10.13. Входы сумматора по модулю два 12 соединены с выходами элементов И 10.2, 10.6, 10.10, 10.14. Входы сумматора по модулю два 13 соединены с выходами элементов И 10.3, 10.7, 10.11, 10.15. Входы сумматора по модулю два 14 соединены с выходами элементов И 10.4, 10.8, 10.12, 10.16. Выход сумматора по модулю два 11 соответствует младшему разряду произведения, а выход сумматора по модулю два 14 - старшему разряду произведения A(z)B(z) mod p(z).
Рассмотрим работу умножителя по модулю. Пусть A(z)=z3+z2+1 и B(z)=z3+1. Тогда их произведение по модулю p(z)=z4+z+1 равно:
(z3+z2+1)(z3+1)modz4+z+1=(z6+z5+z3+z3+z2+1)modz4+z+1=(z6+z5+z2+1)modz4+z+1=z3+z2+z+1.
В соответствии с выбранными значениями A(z) и B(z) единичный сигнал будет на входах 1, 3, 4, 5, 8 умножителей по модулю, а на остальных - нулевой сигнал. Выходные сигналы сумматоров по модулю два 9.1- 9.6 приведены в таблице 7.
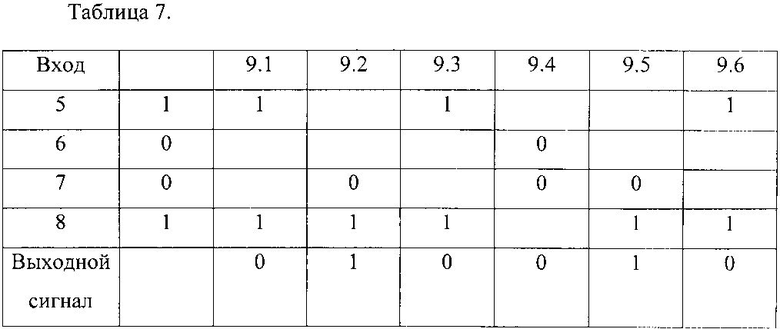
Таким образом, единичный сигнал будет на выходах сумматоров по модулю два 9.2, 9.5.
Выходные сигналы элементов И 10.1- 10.16 приведены в таблице 8.
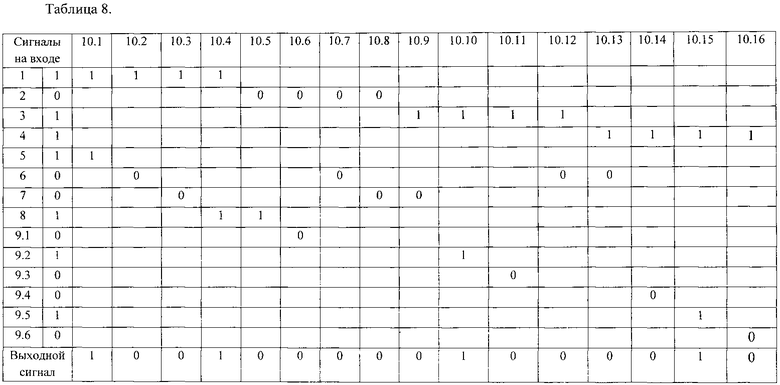
Таким образом единичный сигнал будет на выходе элементов 10.1, 10.4, 10.10, 10.15.
Выходные сигналы сумматоров по модулю два 11-14 определяются из таблиц 9-12.
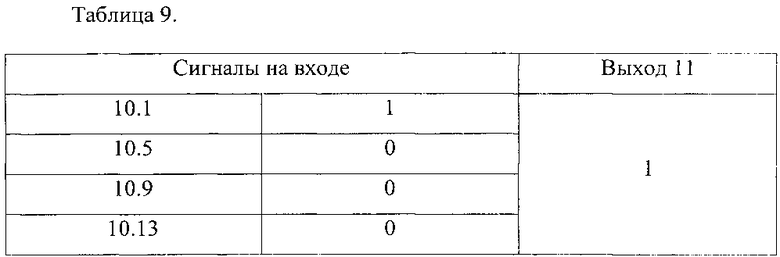
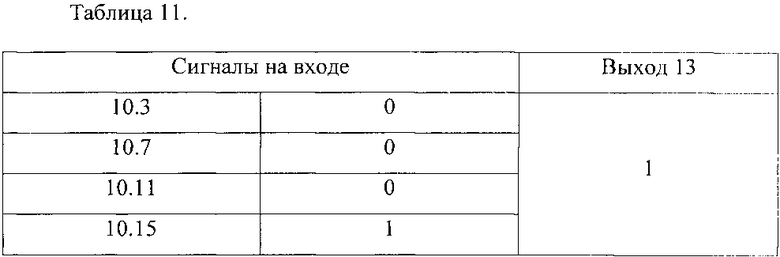

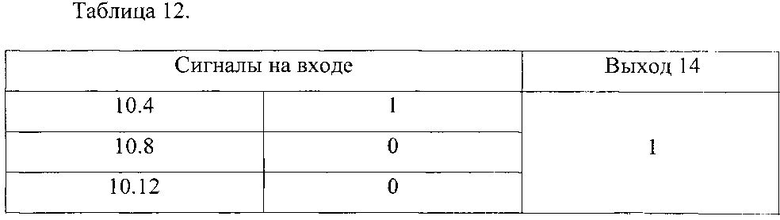

Таким образом, на выходе умножителя по модулю получен двоичный код произведения 1111, который в полиномиальной форме имеет вид z3+z2+z+1, что соответствует контрольному просчету.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство коррекции ошибок в модулярном коде на основе расширения системы оснований | 2017 |
|
RU2652446C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2013 |
|
RU2513915C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С ПЕРЕСЧЕТОМ ОРТОГОНАЛЬНЫХ БАЗИСОВ | 2005 |
|
RU2298873C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2409840C2 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ С КОРРЕКЦИЕЙ ОШИБОК | 2015 |
|
RU2584495C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ | 2005 |
|
RU2300801C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2010 |
|
RU2453902C2 |
| УСТРОЙСТВО РАСШИРЕНИЯ ОСНОВАНИЙ МОДУЛЯРНОГО КОДА | 2014 |
|
RU2562366C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
Изобретение относится к области вычислительной техники и может быть использовано в цифровых вычислительных устройствах, а также в устройствах для формирования элементов конечных полей. Техническим результатом, является снижение аппаратных затрат на реализацию умножителя по модулю. Устройство содержит: 16 двухвходовых элементов И, 6 двухвходовых сумматоров по модулю два, 4 многовходовых сумматоров по модулю два и связи между ними. 1 ил., 12 табл.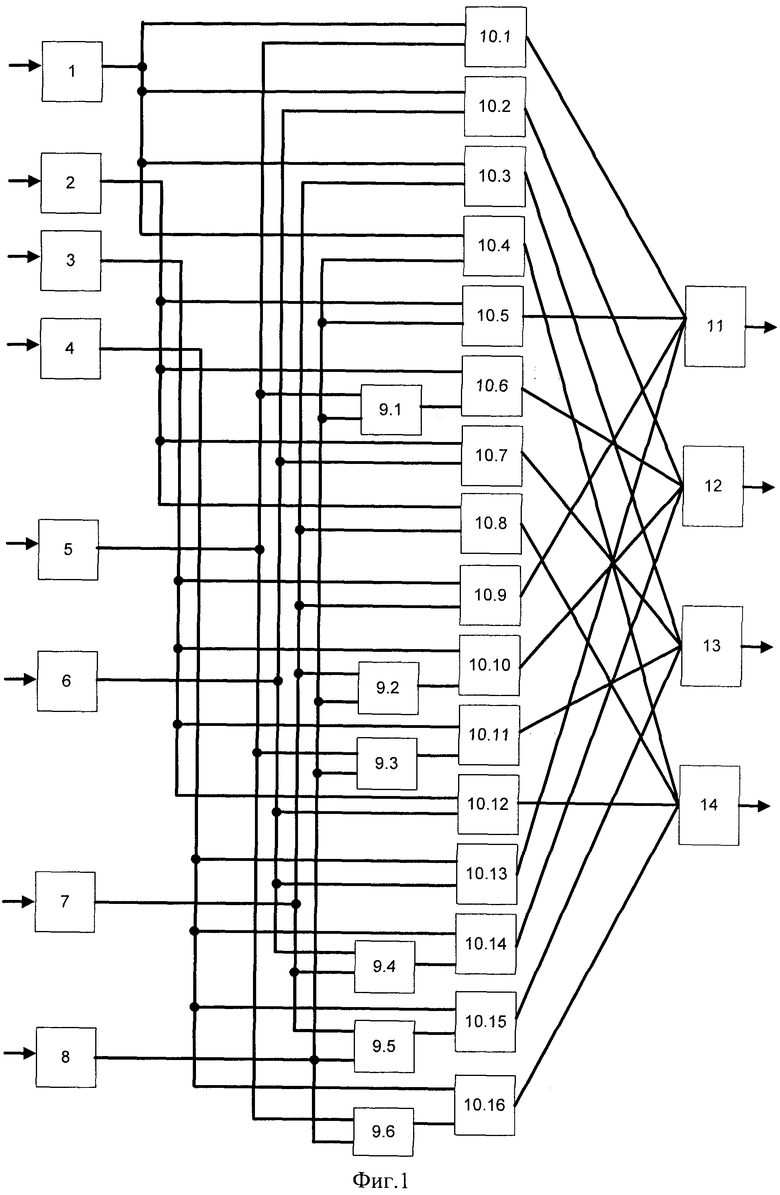
1. Умножитель по модулю имеет четыре входа для первого операнда, четыре входа для второго операнда, шесть двухвходовых сумматоров по модулю два, 16 элементов И, четыре многовходовых сумматора по модулю два, при этом младшие разряды первого и второго операндов поступают на первый и пятый входы соответственно, а старший разряд операндов - соответственно на четвертый и восьмой входы умножителя по модулю, первый вход умножителя по модулю подключен к первым входам 1-4 элементов И, второй вход подключен к первым входам 5-8 элементов И, третий вход подсоединен к первым входам 9-12 элементов И, четвертый вход умножителя подключен к первым входам 13-16 элементов И, пятый вход умножителя - ко второму входу первого элемента И, а также к первым входам 1, 3, 6 двухвходовых сумматоров по модулю два, шестой вход умножителя по модулю подсоединен ко вторым выходам 2, 7, 12, 13 элементов И и к первому входу 4 двухвходового сумматора по модулю два, седьмой вход умножителя по модулю подключен ко вторым входам 3, 8, 9 элементов И, первому входу 2 и 5, а также ко второму входу 4 двухвходовых сумматоров по модулю два, восьмой вход умножителя по модулю подсоединен ко вторым входам 4 и 5 элементов И и вторым входам 1, 2, 3, 5, 6 двухвходовых сумматоров по модулю два, выходы 1-6 двухвходовых сумматоров по модулю два подключены ко вторым входам 6, 10, 11, 14, 15, 16 элементов И соответственно, вход первого многовходового сумматора по модулю два подключен к выходам 1, 5, 9, 13 элементов И, вход второго многовходового сумматора по модулю два подключен к выходам 2, 6, 10, 14 элементов И, вход третьего многовходового сумматора по модулю два подключен к выходам 3, 7, 11, 15 элементов И, вход четвертого многовходового сумматора по модулю два подключен к выходам 4, 8, 12, 16 элементов И, выходы многовходовых сумматоров по модулю два являются выходом умножителя по модулю, причем выход первого многовходового сумматора по модулю два соответствует нулевому разряду произведения, а выход четвертого многовходового сумматора по модулю два - старшему разряду произведения.
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2005 |
|
RU2299461C1 |
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ ЧИСЕЛ ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2006 |
|
RU2316042C1 |
| EP 1855190 A2, 14.11.2007 | |||
| ПРЕСС-ФОРМА ДЛЯ ЛИТЬЯ ПО ВЫПЛАВЛЯЕМЫМ МОДЕЛЯМ | 1991 |
|
RU2037357C1 |
Авторы
Даты
2016-07-10—Публикация
2015-03-10—Подача