Изобретение относится к области машиностроения, к узлам и деталям машин, общим способам и устройствам, обеспечивающим нормальную эксплуатацию машин и установок, к передачам с рычагами, к направляющим механизмам для получения прямолинейного движения. В технической литературе указанная область машиностроения связана с преобразованием вращательного или качательного движения в прямолинейное движение рабочей точки. Часто в старинной технической литературе механизмы с таким назначением называют прямилами, а составляющие их рычаги раньше называли суставами, поэтому можно встретить термин суставного механизма-прямила. Это было связано с развитием паровых машин, в которых прямолинейное движение поршня необходимо было преобразовать в круговое движение вала, передать вращающий момент и энергию потребителям, при необходимости опять преобразовать движение в прямолинейное для обеспечения работы промышленного оборудования. Назначением таких механизмов является получение прямолинейной траектории рабочей точки. В технике есть два вида прямил - приближенные и точные. Приближенные прямила позволяют получить траекторию рабочей точки, близкую к прямолинейной, а точные прямила обеспечивают строгое математическое прямолинейное движение рабочей точки. Приближенный вид прямил применяется, например, в шагающих машинах, где не требуется точное движение рабочей точки по прямой из-за неровностей опорной поверхности. Точный вид прямил применяется в чертежных инструментах, приборах, точном машиностроении. Областью предлагаемого изобретения являются точные механизмы с точным прямолинейным движением.
Сущность изобретения заключается в получении точного прямолинейного движения одновременно двух рабочих точек механизма в противоположных направлениях. Такая задача актуальна, например, для точных лабораторных весов, в которых две чашки с подвесами на рабочих точках не должны смещаться в сторону, должны двигаться строго по прямым линиям, чтобы не изменялись плечи весов, но движение должно быть в противоположных направлениях: если одна чашка опускается, то другая поднимается, и наоборот.
Первым аналогом является приближенное прямило в виде лямбдаобразного механизма Пафнутия Львовича Чебышева [Полное собрание сочинений П.Л. Чебышева. Том. 4. Теория механизмов. - Москва-Ленинград: Издательство Академии наук СССР, 1948 г. - С. 165. - Статья П.Л. Чебышева в этой книге «О преобразовании вращательного движения в движение по некоторым линиям» на стр. 161-165. Электронный режим доступа https://tcheb.ru/plantigrade-machine/]. Этот аналог является классическим для всех шарнирно-рычажных прямолинейных направляющих механизмов, потому что лямбдаобразный механизм обеспечивает прямолинейное движение рабочей точки, но недостатком является не точная прямая линия траектории, а приближенная. Значит, в точном машиностроении и приборостроении лямбдаобразный механизм применять не целесообразно.
Второй аналог - это механизм шагающей машины [Патент RU 2712370 С2, Скворцова А.А. Механизм шагающей машины. - Заявка 2017138076. - Приоритет 01.11.2017. - Рег. 28.01.20. - Публ. заявки 06.05.2019, Бюл. №13. - Публ. Патента 28.01.2020, Бюл. №4. - Электронный ресурс: https://wwwl.fips.ru/registers-doc-view/fips_servlet?DB=RUPAT&DocNumber=201713 8076&TypeFile=html]. Этот механизм доказывает возможность применения приближенного прямила в транспортных средствах и тренажерах, но не в точном машиностроении. Недостаток приближенных прямил общий, в них нет точного прямолинейного отрезка траектории рабочей точки.
Третий аналог выбран в качестве прототипа - это прямило Липкина [Прямило Липкина / Математические этюды. Андреев Н.Н. и др. Электронный ресурс: https://etudes.ru/etudes/lipkin-inversor/]. Описание и размеры прямила Липкина, с более точным и современным названием «Шарнирно-рычажный прямолинейно-направляющий механизм Поселье-Липкина» приведены в книге [Артоболевский И.И. Механизмы в современной технике. В 7 томах. Справочное пособие для инженеров, конструкторов и изобретателей. Издание второе, переработанное. Том 1. Элементы механизмов. Простейшие рычажные и шарнирно-рычажные механизмы. - М.: Наука, Главная редакция физико-математической литературы, 1979. - 496 с. - С. 344, Номер механизма 664. - Электронный ресурс: https://studfile.net/preview/996752/page:35/].
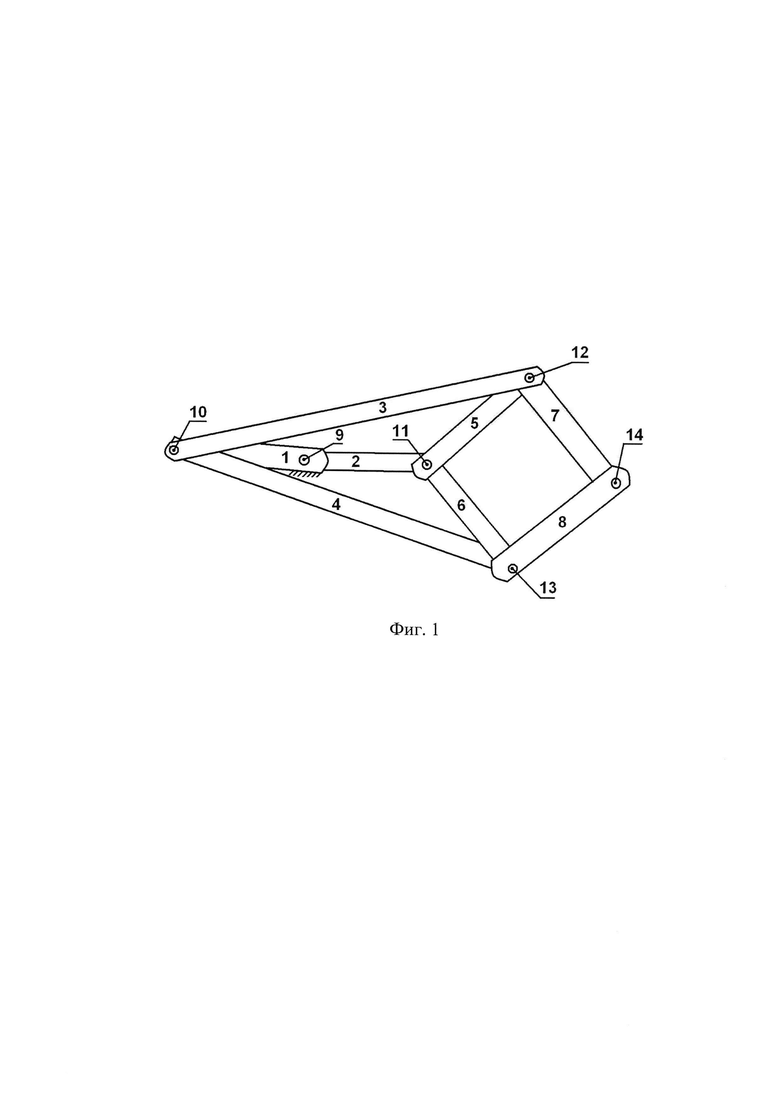
Фиг. 1 показывает общую схему механизма Посселье-Липкина. Механизм Липкина - это семизвенный, не считая корпуса, плоский шарнирно-рычажный механизм, На схеме введены следующие обозначения:
1 - неподвижный корпус механизма Липкина с двумя шарнирами 1 и 10;
2 - качающееся короткое коромысло;
3, 4 - два одинаковых качающихся длинных коромысла;
5, 6, 7, 8 - четыре одинаковых коротких шатуна;
9 - одиночный шарнир, соединяющий корпус 1 и качающееся короткое коромысло 2;
10 - двойной шарнир, соединяющий корпус 1 и два качающиеся длинные коромысла 3 и 4;
11 - двойной шарнир, соединяющий качающееся короткое коромысло 2 и шатуны 5 и 6;
12 - двойной шарнир, соединяющий качающееся длинное коромысло 3 и шатуны 5 и 7;
13 - двойной шарнир, соединяющий качающееся длинное коромысло 4 и шатуны 6 и 8;
14 - одиночный шарнир, соединяющий шатуны 7 и 8.
В классической схеме механизма расстояние между шарнирами 9 и 10 должно быть равно расстоянию между шарнирами 9 и 11. Шатуны 5, 6, 7, 8 имеют одинаковую длину. Шатуны 3 и 4 имеют одинаковую длину. Размеры рычагов могут быть произвольными, лишь бы удовлетворяли условию сборки устройства и возможности движения рычагов.
Механизм Липкина имеет одну степень свободы. Что подтверждается формулой П.Л. Чебышева для расчета числа степеней свободы Cm плоского шарнирно-рычажного механизма: Cm=3P-2S, в которой Р - число рычагов, S - число шарниров, считая их кратность. Учитывая, что в механизме Липкина Р=7; S=2×1+4×2=10, получаем одну степень свободы Cm=3×7-2×10=21-20=1. Значит, например, угол поворота качающегося короткого коромысла 2, безразлично, в какую сторону, однозначно определит положение всех других рычагов и точек механизма.
Отличительная особенность и главное назначение механизма Липкина заключается в преобразовании движения одной точки по дуге окружности в движение другой точки строго по прямой линии. Двойной шарнир 11 двигается по дуге окружности, а одиночный шарнир 14 двигается строго по прямой линии, на рисунке вверх или вниз. Липкин и, тем более, Посселье, не смогли строго доказать движение шарнира 14 по прямой линии с механической точки зрения, хотя математически Липкин привел полное обоснование в виде инверсии окружности. Только через полвека Академик Иван Иванович Артоболевский строго доказал, что для получения точного, а не приближенного, движения точки по прямой линии механизм должен иметь не менее семи рычагов, как в прямиле Липкина. Ранее Пафнутий Львович Чебышев применял приближенные прямила, в том числе свой знаменитый трехзвенный лямбдаобразный механизм, который иногда называют механизмом Хойкена.
В результате анализа литературы была высказана гипотеза о реальной возможности создания механизма подвески перемещением двух рабочих точек по строго вертикальным линиям, естественно, без изменения расстояния между этими рабочими параллельными прямыми. Для решения такой задачи надо доработать механизм Липкина. Содержательная формулировка задачи заключается в создании механизма с двумя рабочими точками. В классическом механизме Липкина рабочей точкой является только одиночный шарнир 14. Значит, надо применить два связанных друг с другом механизма Липкина.
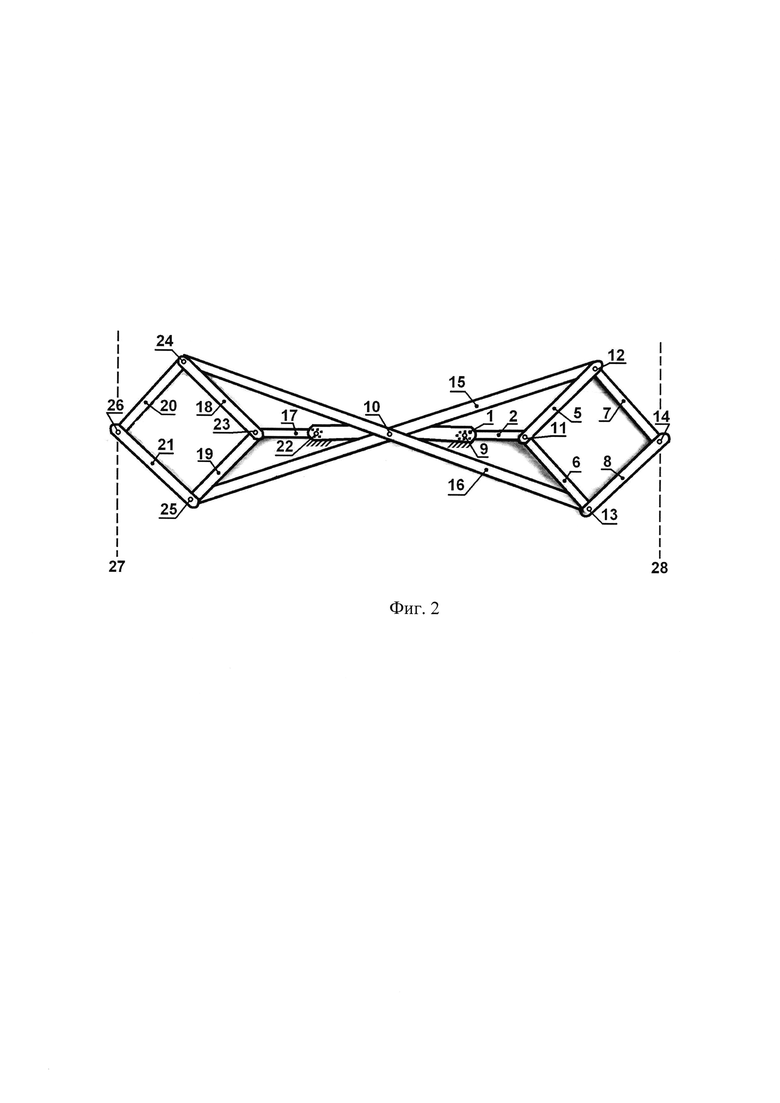
Новым авторским предложением является новый вариант совмещения двух механизмов Липкина в едином устройстве, в результате чего количество рычагов уменьшается на два. Фиг. 2 показывает схему нового механизма.
Нумерация деталей 1-14 сохранена прежней, но совмещение двух механизмов потребовало уточнения, к какой части нового устройства принадлежит деталь, к правой или левой на схеме:
1 - неподвижный корпус двух механизмов Липкина, на котором, в отличие от прототипа, установлены три шарнира 1, 10, 22;
2 - качающееся короткое коромысло правого механизма Липкина;
два качающиеся длинные коромысла 3 и 4 исключены, заменены другими рычагами 15 и 16;
5, 6, 7, 8 - четыре одинаковых коротких шатуна правого механизма Липкина;
9 - одиночный шарнир, соединяющий корпус 1 и качающееся короткое коромысло 2 правого механизма Липкина;
10 - двойной шарнир, соединяющий корпус 1 и два новые рычага 15 и 16, принадлежащие одновременно правому и левому механизмам Липкина;
11 - двойной шарнир, соединяющий качающееся короткое коромысло 2 и шатуны 5 и 6 правого механизма Липкина;
12 - двойной шарнир, соединяющий новый рычаг 15, то есть двойное длинное коромысло, и шатуны 5 и 7 правого механизма Липкина;
13 - двойной шарнир, соединяющий новый рычаг 16, то есть двойное длинное коромысло, и шатуны 6 и 8 правого механизма Липкина;
14 - одиночный шарнир, соединяющий шатуны 7 и 8 правого механизма Липкина, как в прототипе.
Отличительными признаками нового механизма являются новые элементы:
15, 16 - два одинаковые двойные длинные коромысла правого и левого механизма Липкина;
17 - качающееся короткое коромысло левого механизма Липкина;
18, 19, 20, 21 - четыре одинаковых коротких шатуна левого механизма Липкина;
22 - одиночный шарнир, соединяющий корпус 1 и качающееся короткое коромысло 17 левого механизма Липкина;
23 - двойной шарнир, соединяющий качающееся короткое коромысло 17 и шатуны 18 и 19 левого механизма Липкина;
24 - двойной шарнир, соединяющий новый рычаг 16, то есть двойное длинное коромысло 16, и шатуны 18 и 20 левого механизма Липкина;
25 - двойной шарнир, соединяющий новый рычаг 15, то есть двойное длинное коромысло 15, и шатуны 19 и 21 левого механизма Липкина;
26 - одиночный шарнир, соединяющий шатуны 20 и 21 левого механизма Липкина.
Получилось, что два механизма Липкина, правый и левый, соединены друг с другом двумя новыми рычагами в виде двух одинаковых двойных коромысел 15 и 16 при удлиненном корпусе 1. Математически новое устройство получается отображением схемы прототипа с помощью центральной симметрии, то есть поворота на угол 180 градусов вокруг двойного шарнира 10. В нейтральном положении (фиг. 2), новый механизм обладает не только свойством центральной симметрии, но дополнительно имеет две оси симметрии. Горизонтальная ось симметрии проходит через точки шарниров 26, 23, 22, 10, 9, 11, 14, как в прототипе. Однако в прототипе отсутствует вертикальная ось симметрии, а в новом механизме она есть, проходит через точку 10 шарнира. При отклонении рычагов от нейтрального положения обе осевые симметрии нарушаются, но центральная симметрия сохраняется всегда. Это отличительные признаки новой схемы механизма.
Новизной предлагаемого технического решения и отличительным признаком являются две рабочие точки механизма (14 и 26), а не одна, как в классическом механизме Липкина. В прототипе (фиг. 1) строго по прямой линии двигается только одна рабочая точка - это шарнир 14. В предлагаемом новом механизме (фиг. 2) строго по двум параллельным прямым линиям двигаются одновременно две рабочие точки - это прежний шарнир 14, но теперь уже правого механизма Ликина, и новый шарнир 26 добавленного нового левого механизма Липкина. Далее приняты два следующих обозначения: 28 - это прямая линия, по которой двигается шарнир 14 правого механизма Липкина, 27 - это прямая линия, по которой двигается шарнир 26 левого механизма Липкина. Направления движения шарниров 14 и 26 взаимно противоположны, но как бы не отклонялись рычаги в допустимых пределах, прямые линии 27 и 28 сохраняют свое положение.
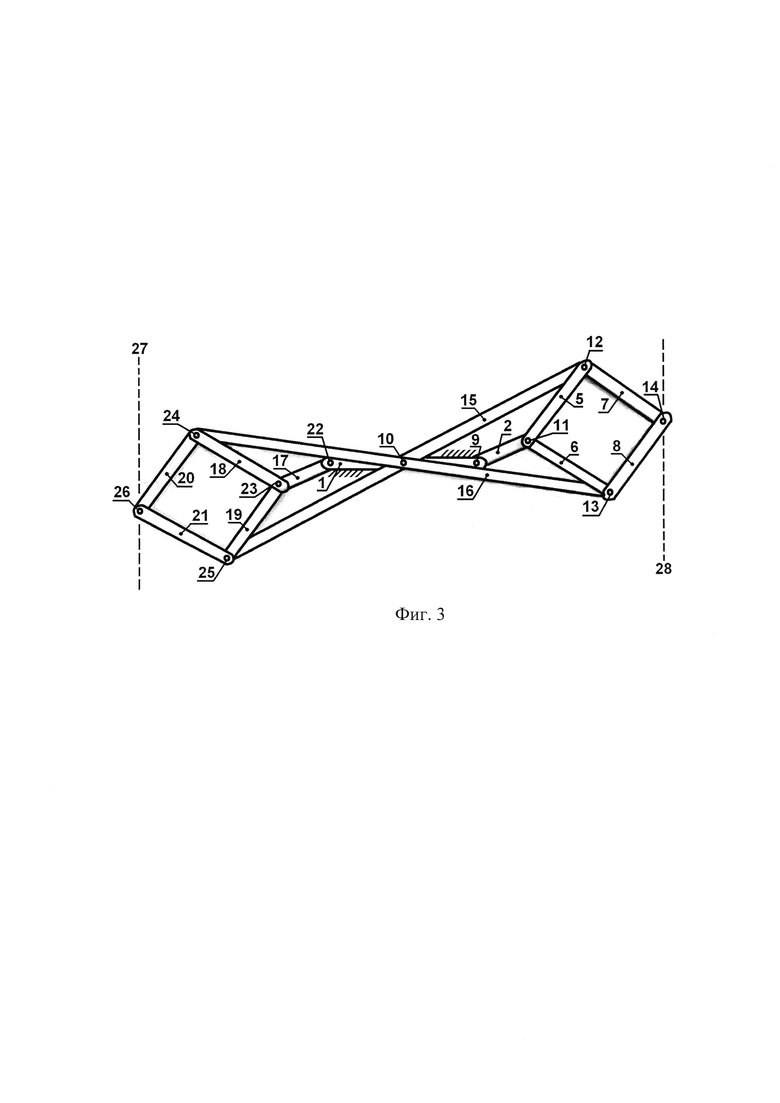
Фиг. 3 иллюстрирует сравнительно небольшое отклонение рычагов от нейтрального положения. Рабочие точки 14 и 26 двигаются строго по фиксированным прямым линиям 28 и 27 соответственно. Математическое доказательство этого факта сводится к рассмотрению каждого единичного механизма Липкина в отдельности от другого, правого или левого. Второй механизм Липкина повторяет движение первого, но с отображением по правилам центральной симметрии, то есть поворотом на 180 градусов. Дополнительного обоснования требует доказательство одной степени свободы механизма. Для этого надо применить указанную ранее формулу П.Л. Чебышева для определения количества степеней свободы плоского шарнирно-рычажного механизма: Cm=3P-2S, в которой Р - число рычагов, S - число шарниров, считая их кратность. Учитывая, что в новом, сдвоенном механизме Липкина Р=12 (число рычагов удвоилось, но длинные коромысла 3 и 4 удваивать не нужно, потому что они заменены теми же двумя двойными длинными коромыслами 15 и 16); S=2(2×1+4×2)-2=18 (число шарниров удвоилось, но двукратный шарнир 10 остается одним, общим для обоих механизмов Липкина, правого и левого), получаем, казалось бы, нуль степеней свободы Cm=3×12-2×18=36-36=0. Но на практике этот механизм работает с одной степенью свободы. Никакого парадокса здесь нет, потому что в шарнирно-рычажных механизмах есть понятие пассивного звена. Пассивное звено не влияет на движение механизма и число степеней свободы. В предлагаемом механизме можно исключить, например, качающееся короткое коромысло левого механизма Липкина 17, тогда Р=11; S=16; Cm=3×11-2×16=33-32=1. Можно также исключить качающееся короткое коромысло правого механизма Липкина 2. Оно исключать из схемы одновременно два указанных рычага 17 и 2 нельзя, потому что только один из них является пассивным кинематическим звеном. Как только одно пассивное звено, рычаг 17 или 2, будет исключено, оставшееся звено станет активным рычагом. На следующих схемах пассивное звено 17 или 2 не исключено. Пассивные звенья часто применяют для повышения надежности или балансировки механизма, то есть его симметрии, а также для уменьшения вибрации и повышения точности движения рабочих точек. Получается, что предлагаемый сдвоенный механизм Липкина имеет одну степень свободы и одно пассивное звено (2 или 17). Значит, положение рычагов полностью определяется одной независимой координатой, обычно углом отклонения короткого коромысла 2 от горизонтали. Фиг. 3 иллюстрирует случай отклонения правого механизма Липкина вверх, а левого механизма Липкина вниз. При этом центральная симметрия, то есть поворот на 180 градусов, конфигурации в целом сохраняется.
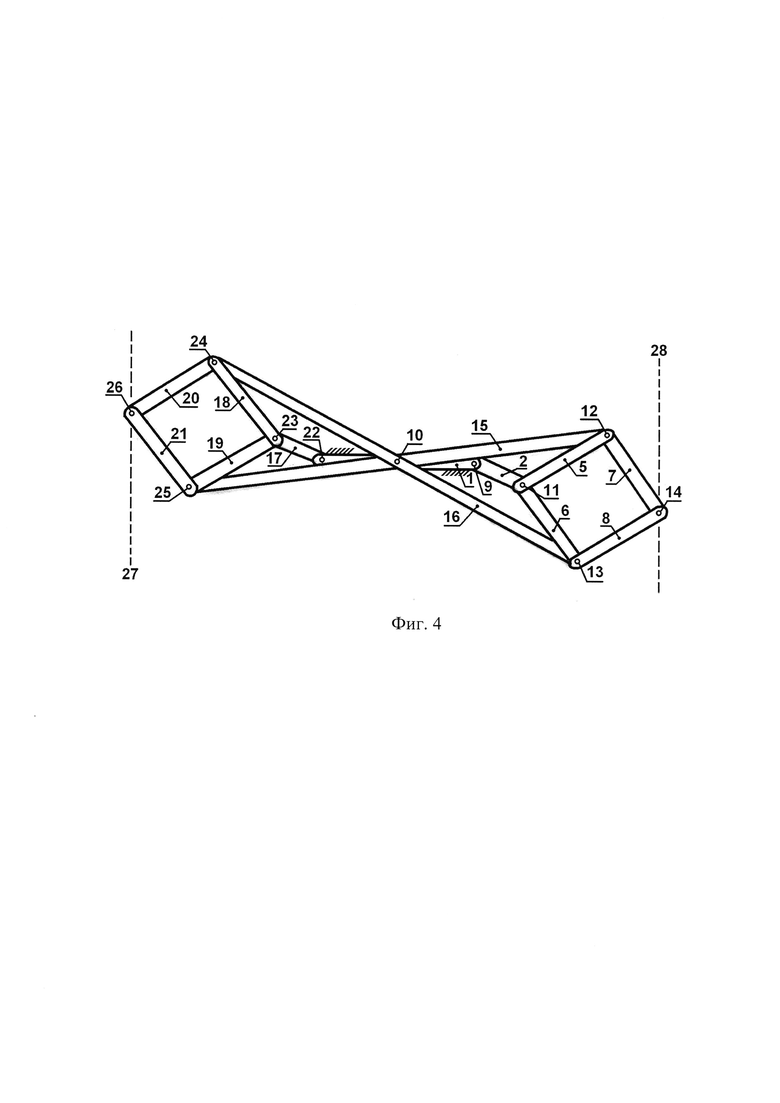
Фиг. 4 иллюстрирует аналогичное предыдущему небольшое отклонение сдвоенного механизма Липкина от нейтрального положения, но только в противоположном направлении. Правый механизм Липкина сместился вниз, а левый механизм Липкина сместился вверх. Главное то, что рабочие точки, то есть шарниры 14 и 26, всегда перемещаются строго по параллельным прямым линиям 28 и 27 соответственно.
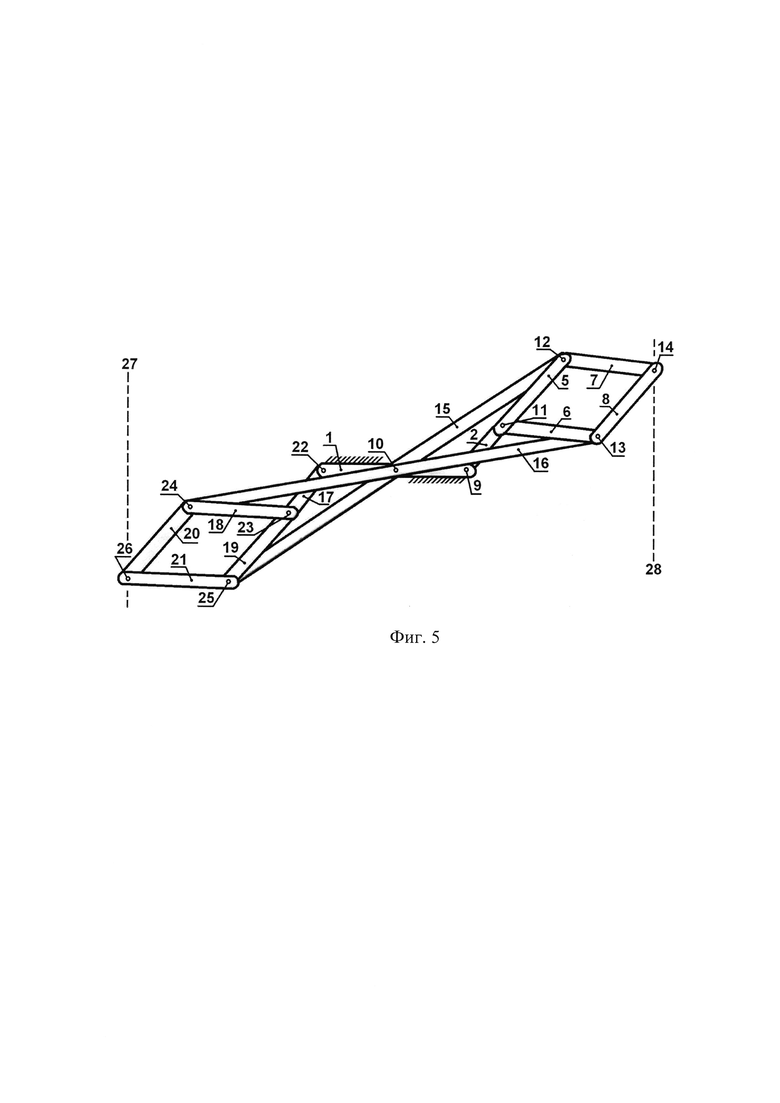
Фиг. 5 иллюстрирует уже не малое, а среднее отклонение сдвоенного механизма Липкина от нейтрального положения. При этом правый механизм Липкина сместился вверх, а левый механизм Липкина переместился вниз. Отклонения обоих механизмов значительно больше, чем на двух предыдущих иллюстрациях (фиг. 3 и фиг. 4). Такие отклонения вполне возможны, лишь бы корпус, рычаги и шарниры не мешали двигаться друг другу. Фиг. 5 показывает, что двойное длинное коромысло 16 пересекло шарниры 9 и 22. Значит, надо конструктивно предусмотреть свободу движения. Например, двойное длинное коромысло 16 должно выступать над деталями шарниров 9 и 22. Или, наоборот, детали шарниров 9 и 22 должны быть утоплены в корпус 1. Конструктивных исполнений деталей и их шарнирных соединений может быть несколько, что доказывает работоспособность предлагаемого сдвоенного механизма Липкина.
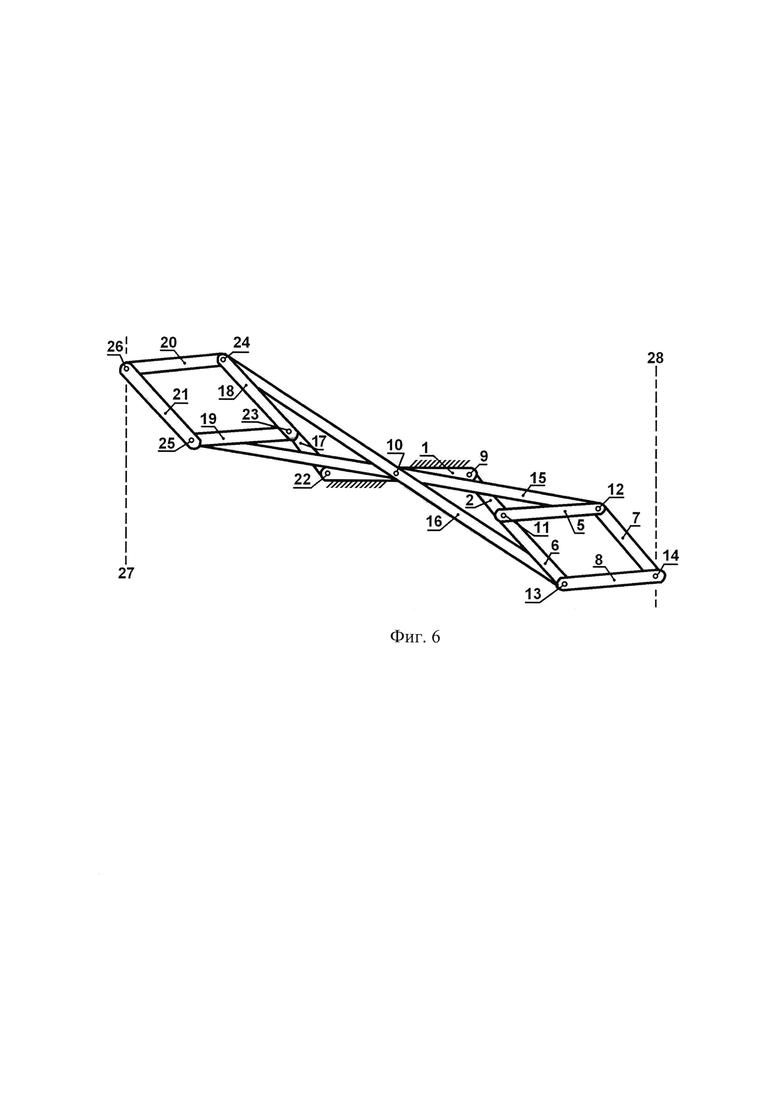
Фиг. 6 показывает такое же среднее отклонение сдвоенного механизма Липкина от нейтрального положения, но в противоположном направлении относительно предыдущей схемы (фиг. 5). При этом правый механизм Липкина сместился вниз, а левый механизм Липкина сместился вверх. Отличием от предыдущей схемы (фиг. 5) является изменение номера детали, пересекающей шарниры 9 и 22. Теперь их пересекает двойное длинное коромысло 15, а не двойное длинное коромысло 16, как на предыдущей иллюстрации (фиг. 5). Значит, двойное длинное коромысло 15 и шарниры 9 и 22 тоже не должны мешать друг другу при движении рычагов, если требуются не малые, а средние отклонения сдвоенного механизма Липкина от нейтрального положения. При средних смещениях сохраняется главное свойство сдвоенного механизма Липкина - обе рабочие точки, то есть шарниры 14 и 26, двигаются строго по параллельным прямым линиям 28 и 27 соответственно.
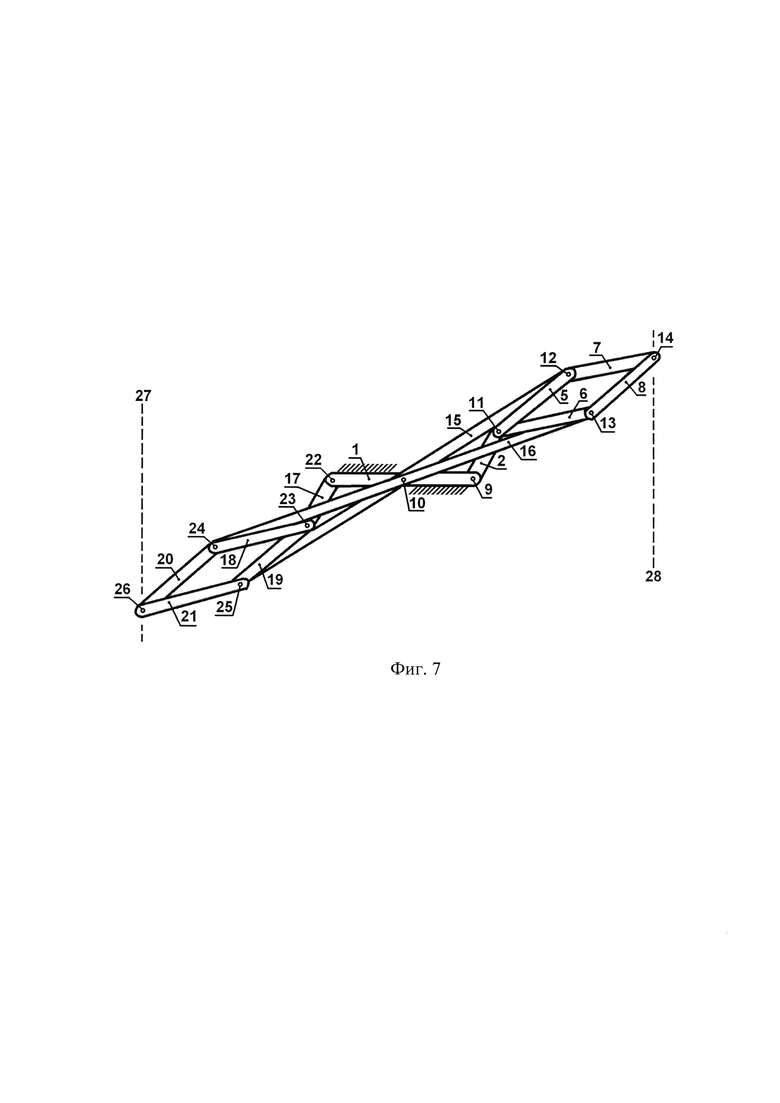
Фиг. 7 показывает большое отклонение сдвоенного механизма Липкина от нейтрального положения. При этом правый механизм Ликина поднялся, а левый механизм Липкина опустился. Под большим отклонением механизма будем понимать случай, когда двойные длинные коромысла 15 и 16 вплотную приблизились к шарнирам 11 и 23. Вряд ли есть смысл рассматривать такие отклонения и, тем более, увеличенные отклонения, больше указанных. На практике, например, в механизмах весов, отклонения рычагов всегда малые, часто даже не заметны визуально.
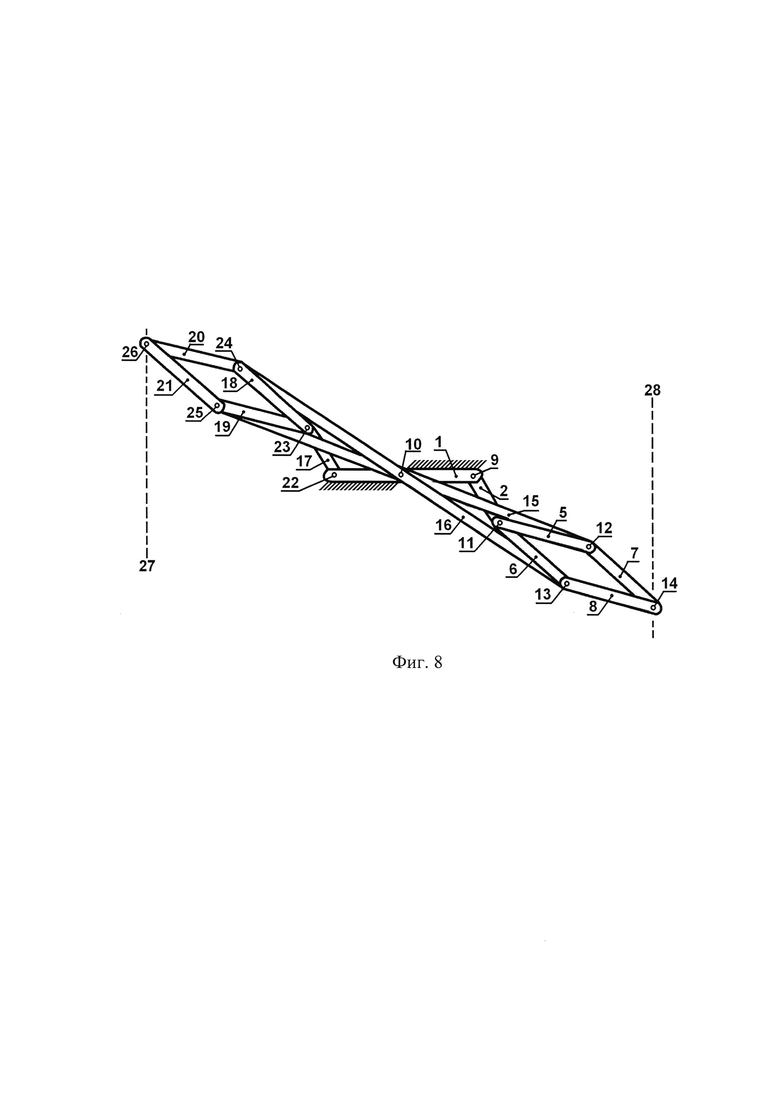
Фиг. 8 показывает большие отклонения рычагов в другом направлении, когда правый механизм Ликина опустился, а левый механизм Липкина поднялся.
В подвесках автомобилей тоже есть ограничения на ход деталей, например, амортизаторов, превышение которых приводит к громкому стуку и даже поломке подвески автомобиля. В исполнительных механизмах систем управления самолетами, ракетами, космическими аппаратами, кораблями перемещения рычагов тоже ограничены, вполне достаточно малых и средних величин. Главное то, что даже при больших отклонениях механизма от нейтрального положения обе рабочие точки, то есть шарниры 14 и 26, двигаются строго по прямым линиям 28 и 27 соответственно.
Для доказательства работоспособности и практической осуществимости предлагаемого нового технического решения была изготовлена действующая модель нового механизма (фиг. 9). Действующая модель доказала, что крайние шарнирные рабочие точки 14 и 26 двигаются строго по взаимно параллельным прямым линиям в противоположных направлениях.
Фиг. 10 представляет технический результат изобретения на примере сравнения двух типов лабораторных весов. Первая и вторая схема сверху показывают коромысловые лабораторные весы, какие часто применяют на школьных уроках, например, для демонстрации закона Архимеда. Вытесняемую воду надо направить в стакан, поставленный на чашку весов. Но чашка коромысловых весов смещается, и вода может пролиться мимо стакана. Этот недостаток устраняется применением в весах предлагаемого нового механизма, показанного внизу рисунка (фиг. 10). Нет смысла изображать несколько положений прибора, как в случае коромысловых лабораторных весов, потому что чашки на подвесах в рабочих точках не смещаются ни вправо, ни влево, всегда перемещаются параллельно по вертикальным прямым в противоположных направлениях.
Таким образом, основная техническая задача решена. Предложен новый сдвоенный механизм Липкина с одним пассивным коротким коромыслом, в котором две рабочие точки двигаются строго по параллельным друг другу прямым линиям, постоянно фиксированным относительно корпуса. Предложенный механизм имеет широкое общетехническое применение.
| название | год | авторы | номер документа |
|---|---|---|---|
| ШАГАЮЩИЙ МЕХАНИЗМ | 2021 |
|
RU2801819C2 |
| МЕХАНИЗМ ПОССЕЛЬЕ-ЛИПКИНА С ВЫХОДНЫМ РАБОЧИМ ЗВЕНОМ | 2020 |
|
RU2750344C1 |
| МЕХАНИЗМ ПОСЕЛЬЕ-ЛИПКИНА С КУЛИСНЫМ РЫЧАГОМ | 2013 |
|
RU2527642C1 |
| ПЛАВУЧЕ-ШАГАЮЩИЙ ДОННЫЙ АППАРАТ | 2001 |
|
RU2214940C2 |
| МЕХАНИЗМ ШАГАЮЩЕЙ МАШИНЫ | 2017 |
|
RU2712370C2 |
| МЕХАНИЗМ РЕЗАНИЯ ЛЕСОПИЛЬНОЙ РАМЫ | 1992 |
|
RU2036079C1 |
| Двухтактный поршневой двигатель внутреннего сгорания | 2021 |
|
RU2776460C1 |
| Привод режущего аппарата | 1990 |
|
SU1762788A1 |
| Двухтактный поршневой двигатель внутреннего сгорания | 2020 |
|
RU2739104C1 |
| ШАРНИРНЫЙ ПРЯМОЛИНЕЙНО НАПРАВЛЯЮЩИЙ МЕХАНИЗМ | 1993 |
|
RU2075672C1 |


Изобретение относится к машиностроению. Направляющий рычажно-шарнирный механизм содержит корпус, короткое качающееся коромысло, два длинных качающихся коромысла и четыре одинаковых шатуна, соединенных шарнирно в виде сборки ромба. Первые концы длинных коромысел соединены шарнирно с корпусом в общей точке, вторые концы длинных коромысел соединены шарнирно с двумя противоположными вершинами ромба. Короткое коромысло соединено шарнирно одним концом с корпусом, а вторым с третьей вершиной ромба, четвертая вершина ромба является первой рабочей точкой механизма, совершающей точное прямолинейное движение по первой прямой линии. Длинные коромысла продолжены прямолинейно и выполнены в два раза большей длины по правилу центральной симметрии относительно общей точки соединения первых концов длинных коромысел. На продолжении двух длинных коромысел по правилу центральной симметрии относительно общей точки соединения первых концов длинных качающихся построен такой же механизм со второй рабочей точкой механизма, центрально симметричной первой рабочей точке механизма, совершающей точное прямолинейное движение по второй прямой линии, которая параллельна первой прямой линии. Рабочие точки механизма двигаются в противоположных направлениях. Обеспечивается одновременное прямолинейное движение двух точек в противоположных направлениях. 10 ил.
Направляющий рычажно-шарнирный механизм для одновременного прямолинейного движения двух точек в противоположных направлениях, содержащий корпус, короткое качающееся коромысло, два длинных качающихся коромысла, четыре одинаковые шатуна, соединенные шарнирно в виде сборки ромба, первые концы длинных качающихся коромысел соединены шарнирно с корпусом в общей точке, вторые концы длинных качающихся коромысел соединены шарнирно с двумя противоположными вершинами сборки ромба из одинаковых шатунов, короткое качающееся коромысло соединено шарнирно одним концом с корпусом, другой конец короткого качающегося коромысла соединен с третьей вершиной сборки ромба из одинаковых шатунов, четвертая вершина сборки ромба является первой рабочей точкой механизма, совершающей точное прямолинейное движение по первой прямой линии, отличающийся тем, что длинные качающиеся коромысла продолжены прямолинейно и выполнены в два раза большей длины по правилу центральной симметрии относительно общей точки соединения первых концов длинных качающихся коромысел, на продолжении двух длинных качающихся коромысел по правилу центральной симметрии относительно общей точки соединения первых концов длинных качающихся коромысел построен такой же механизм, с такими же по размеру рычагами, с таким же соединением рычагов, со второй рабочей точкой механизма, центрально симметричной первой рабочей точке механизма, совершающей точное прямолинейное движение по второй прямой линии, которая параллельна первой прямой линии, при этом первая рабочая точка механизма и вторая рабочая точка механизма двигаются в противоположных направлениях.
| МЕХАНИЗМ ПОССЕЛЬЕ-ЛИПКИНА С ВЫХОДНЫМ РАБОЧИМ ЗВЕНОМ | 2020 |
|
RU2750344C1 |
| МЕХАНИЗМ ПОСЕЛЬЕ-ЛИПКИНА С КУЛИСНЫМ РЫЧАГОМ | 2013 |
|
RU2527642C1 |
| СПОСОБ РАЗДЕЛЕНИЯ ЭТИЛЕНГЛИКОЛЯ И 1,2-БУТАНДИОЛА | 2013 |
|
RU2594159C2 |
| US 20240209925 A1, 27.06.2024. | |||
Авторы
Даты
2025-05-26—Публикация
2024-09-26—Подача