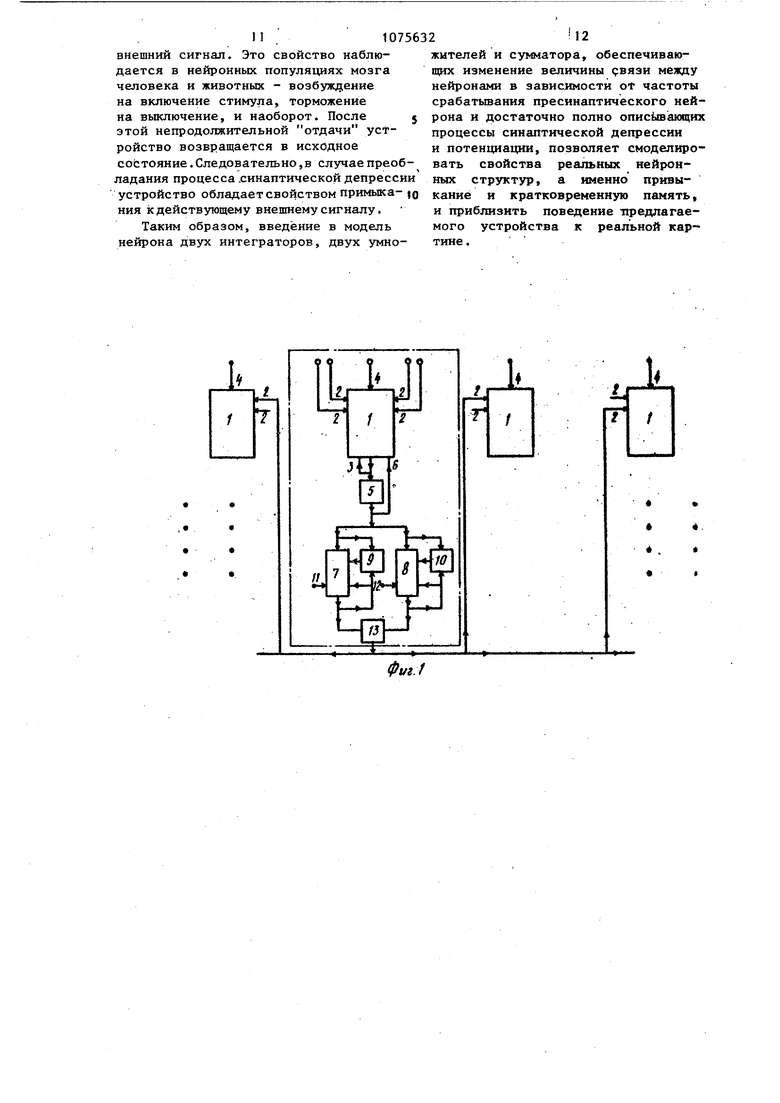
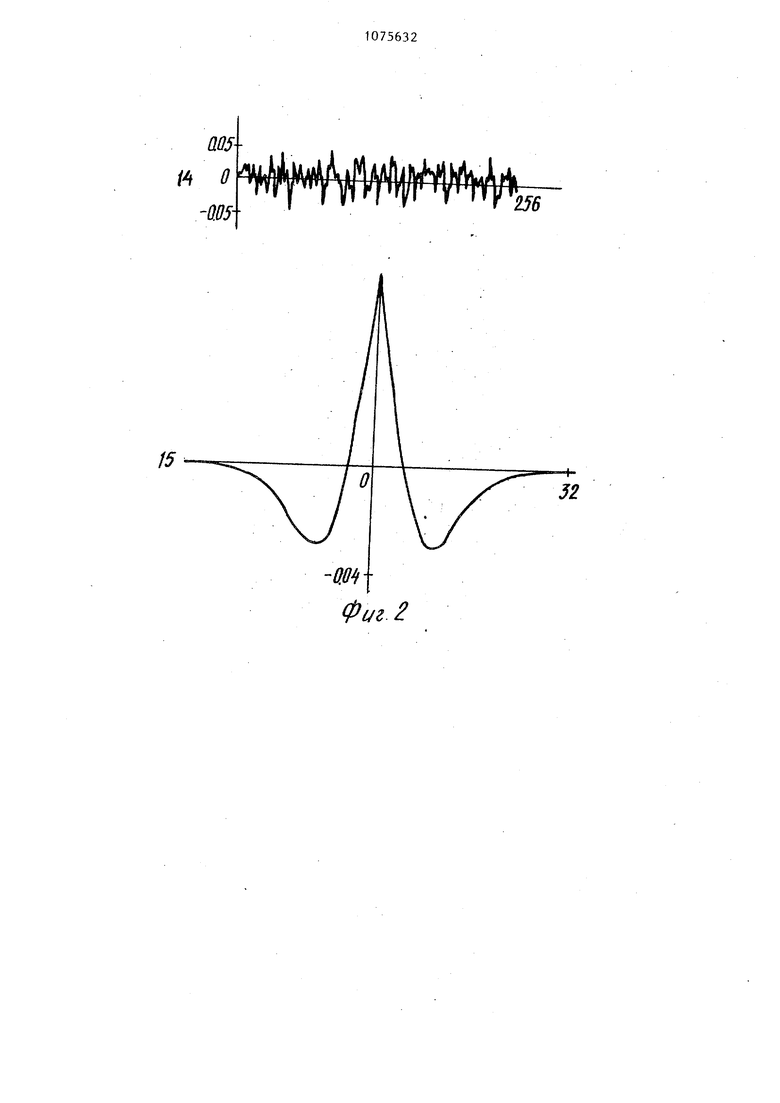
Изобретение относится к области бионики и может использоваться для моделирования поведения нейронньсх структур при обучении и распознавании образов. Известно, устройство для моделиро вания нейрона, входящее в сеть, в которой выходы каждого устройства подключены к входам соседних моделе нейронов с помощью локальных связей (т.е. связей, являющихся убывающими функциями расстояния между клетками слоя) j. Эти устройства, в частности, могут осуществлять операцию выделения краев пространственно распределенного внешнего сигнала, играющую большую роль в центральной нервной системе человека и животных при выделении информативных признаков образов, Однако свойства отдельных моделей нейронов этой сети не соответ ствуют полученным в последние годы данным о синаптической пластичности в нервной системе (т.е., способноети нейронов изменять величину связи с другими нейронами в зависимости от собственной активьгости). Эти экспериментальные данные указывают на участие двух различных процессов в синаптической пластичности, один из которых связан с ис тощением запасов доступного медиат ра при дгп тельной монотонной стиму ляции нейрона и приводит к уменьшению величины связи между нейрона ми (синаптическая депрессия), а другой, по-видимому, связан с регу ляцией внутриклеточного кальция и приводит к увеличеншо связи межд нейронами при такой стимуляции (си наптическая потенциация). I Наиболее близким техническим решением к изобретению является устройство для моделирования нейро нов 2j, содержащее цифровой интегратор, прямой вход которого являетсЯ входом устройства, и цифровые интеграторы потенциации и депрессии, выходы которых подключены соответствующим входам сумматора. Кроме того, устройство содержит це лый ряд других цифровых интеграторов, соединенных между собой и измерителем. Данное устройство также не моду лирует упомянутые выще процессы синаптической пластичности. Оно 2 имеет сложную структуру и его можно использовать при реализации на его основе нейронных сетей. Целью изобретения является повышение точности за счет обеспечения возможности моделировать синаптическую депрессию и потенциацию и упрощение конструкции. Постайленная цель достигается тем, что в устройство для моделирования нейрона, содержащее цифровой интегратор, прямые входыкоторого являются входами возбуждения устройства, и цифровые интеграторы потенциации и депрессии, выходы которых подключены к соответствующим входам сумматора, введены два блока умножения и компаратор, выход которого подключен к первым входам-цифровых интеграторов потенциации и депрессии и блоков умножения, выходы цифровых интеграторов потенциации и депрессии соединены с вторыми своими входами и с вторыми входами соответствующих блоков умножения, выходы которых подключены к третьим входам соответствующих цийровых интеграторов потенциации и депрессии, четвертые входы цифровых интеграторов потецциации и депрессии соединены с источниками постоянного сигнала, выход цифрового интегратора подключен к первому инверсному входу цифрового интегратора, второй инверсный вхгд которого соединен с выходом компаратора, выходом устройства является выход сумматора. Соединение таких устройств в одну структуру с помощью локальных входов дает совершенно новый результат,- определяемый кооперативными свойствами слоя моделей нейронов и явно не вытекающий из исходных предпосьток с синаптической пластичности, а именно полученная в результате модель нейронной структуры обладает способностью к привыканию (т.е. ее реакция на внешний стимул уменьшается со временем) и кратковременной памяти (т.е. структура сохраняет след стимула в течение времени, значительно большего характерных времен депрессии и потенциации). На фиг. 1 приведена структурная схема устройства, где также указаны связи по выходу этого устройства с аналогичными устройствами, которые образуют сеть fl на фиг. 2 - характеристики внешнего сигнала и локальных связей между устройствами нейрона в сети, на фиг. 3 и 4 - пос довательные этапы работы сети в двух различных режимах (соответстве но с преобладанием синаптической потенциации и депрессии). Устройствр для моделирования нейрона содержит цифровой интегратор 1,-группа прямых входов 2 которого соединена с выходами моделей соседних нейронов, а первый инверсный вход 3-е выходом интегратора а прямой вход 4 интегратора 1 соеди нен с источником внешнего сигнала (на чертеже не показан), компаратор 5, вход 6 интегратора, цифровые интеграторы 7, 8 потенциации и депрес сии, блоки умножения 9, 10, источники 11, 12 постоянного сигнала, су матор 13. Выход интегратора 1 связа также с входом компаратора 5, осуществляющего сравнение сигнала на входе с порогом нейрона. Выход компаратора 5 связан обратной связь с В.ТОРЫМ инверсным входом 6 интегратора 1 и входами цифровых интеграторов 7 и 8 потенциации и депрессии. Каждый из интеграторов 7 и 8 имеет четыре входа, первый из которых связан с выходом компаратора 5, третий через блок умножения 9 (10) связан с выходом интегратора 7 (8), а четвертый вход связан с исто ником единичного (по амплитуде) постоянного сигнала 11 (12). Выходы двух интеграторов 7 и В соединены с своими вторыми входами и с входами сумматора 13, выход которого сое динен с входами 2 соседних моделей нейронов. Рассмотрим работу устройства, включенного в указанную сеть. Для задания характера функционирования устройства определяют значения весо подынтегральных функций цифровых интеграторов 1, 7 и 8. и их исходные значения на основе нейрофизиологических данных. После этого устройст во готово к приему внешнего сигнала На каждом шаге на входы 4 интеграторов 1, значения на выходе которых отражают динамику мембранных потенциалов моделируемых нейронов, подаются внешние сигналы, характеризующие сумму постсинаптических потенциалов от внешних источников, на входы 2 - сигналы с выхода соседних моделей нейронов, на входы 3 - сиг- „ налы обратной связи с выходов соот- W ветствующих интеграторов 1, моделирующие наличие постоянной времени мембраны нейрона, на входы 6 сигналы с выходов соответствующих компараторов 5, моделирующие возвращение потенциала мембраны нейрона к исходному уровню после генерации спайка (импульса). Сигналы с выходов интеграторов 1 подаются на соответствующие входы компараторов 5, моделирующих процесс генерации спайка нейрона в случае превышения порога мембранным потенциалом нейрона. Компараторы 5 формируют импульсы единичной длительности (в один шаг) и единичной амплитуды. С выходов компараторов 5 единичные импульсы поступают на входы интеграторов 7 и 8, моделирующих процессы депрессии и потенциации в синаптических окончаниях нейронов. Интеграторы 7 и 8 осуществляют пошаговое интегрирование приходящих на них постоянных единичных сигналов 11 и 12, сигналов с выходов компаратора 5 и выходов интеграторов 7 и 8 соответственно, а также произведений сигнала на выходе компаратора 5 с сигналом на выходе соответственно интеграторов 7 и 8. Сигналы с вькодов интеграторов 7 и 8 поступают на входы сумматоров 13, сигналы с выхода которых подаются на входы 2 интеграторов 1 соседних моделей нейронов с весами, которые определяются на основе нейрофизиологических и психофизиологических данных функцией модуля разности расстояния между моделями нейронов, представленной на графи,ке 15 (фиг. 2). Пошаговая работа описанного устройства соответствует решению следующей системы разностных уравнений, адекватно характеризующих поведение структуры моделируемых нейронов: Р,-(М)-Pi( Р,(.} Z у (г) xj(K)(3/i) Mj(k)-eN,(ic)4S.C4) , ji ( )VS, N. (kijx . (. (kM),-, Xj,,(«)-x.jCk).(i;)x.jlk)C2N.WfI)2, где )- мембранный потенциал i-ro. нейрона, на k -м шаге , 4 - постоянная времени мембраны нейрона;
0 - порог срабатывания нейрона;
5((1с) - внешний сигнал, подаваемый на i-и нейрон на шаге;
Jtr) - функция связи, характеризующая неизменную во времени часть связи между нейронами, модуль разности порядковых номеров который равен Г,
N(1)- дискретная характеристика состояния нейрона на Кгм шаге, определяемая условием: Р(1,) 9 - нейрон генерирует импульс (спайк),
Р (1) -с: б - нейрон молчит j
j(Xj,- величины, характеризующие
/. , переменные во времени части
- 1 J связи от j го нейрона
на k-м шаге, отражающие соответственно вклад процессов синаптической депрессии и потенциации,
D- параметры, характеризующие синаптическую депрессию
Д, 62iS 2 характеризующие синаптическую потенциацию, PaccMOTpiiM поведение модели единичного нейрона под номером i , входящего в моделируемую нейронную сеть. Будем считать время дискретным ,с единичным квантом времени и выведем уравнение, описывающее работу i-ro нейрона на шаге (дискретном интер-вале времени) . Как показывают многочисленные, нейрофизиологические исследования нейрон характеризуется мембранным потенциалом Р- (V. изменяющимся во времени под влиянием внешних воздействий. При достижении мембранным потенциапом определенного порогового уровня б нейрон.генерирует импульс - так называемый поТенциа-1 действия, который передает сигнал от данного нейрона с которым он связан синаптически. Таким образом, нейрон может находиться в двух состояниях: активном
{М;( 1 при P(k)7/e, в котором
происходит генерация потенциала действия и передача сигнала к другим . нейронам, и пассивном (N (-k| О ) при
РДЧ) С 0 , Следует подчеркнуть, что после генерации нейронов потенциала действия мембранный потенциал возвращается в состояние покоя, которое в нашей модели характеризуется Р; (k) 0, т.е. фактически происходит сбрасьшание потенциала на величину, равную порогу срабатьшания в.. Как показано в целом ряде фундаментных нейрофизиологических работ, мембрана нейрона между двумя срабатываниями может быть представлена в виде определенной электрической схемы, содержащей емкость и сопротивление, с постоянной времени l/ot. Изменение мембранного потенциала за единичный квант времени, обусловленное этим пассивным свойством мембраны, равно ,Pj(k). Следовательно, в отсутствие внешних воздействий на нейрон изменение мембранного потенциала за один квант времени удовлетворяет следующему уравнению:
P.iVl)-P(VhoiP 1)-6N,tl),
что- соответствует тому, что при Р;(.)Э мембранный потенциал возвращается к нулевому уровню с постоянной времени f/oC , а при Р-(1с)-6 нейрон генерирует потенциал действия (Ni(1) 1 ) и скачком возвращается в состояние покоя.
Однако в действительности на нейрон в каждый кбант времени могут поступать воздействия от внешних источников сигнала и от соседних нейронов, входящих в моделируемую нейронную сеть. Изменение мембранного потенциала за единичный квант времени, обусловленное этими двумя процес,сами, может быть представлено в виде двух слагаемой: 5i(k) внешНИИ сигнал, подаваемый на i-и нейрон на k-м шаге, {fe)N Д1.)j сумма постсинаптических потенциалов, поступающих на т-й нейрон с остальных нейронов моделируемой структзфы при их срабатьшании (здесь д-,- постсинаптический потенциал, генерируемый на -м нейроне при срабатьшании j-го нейронй).
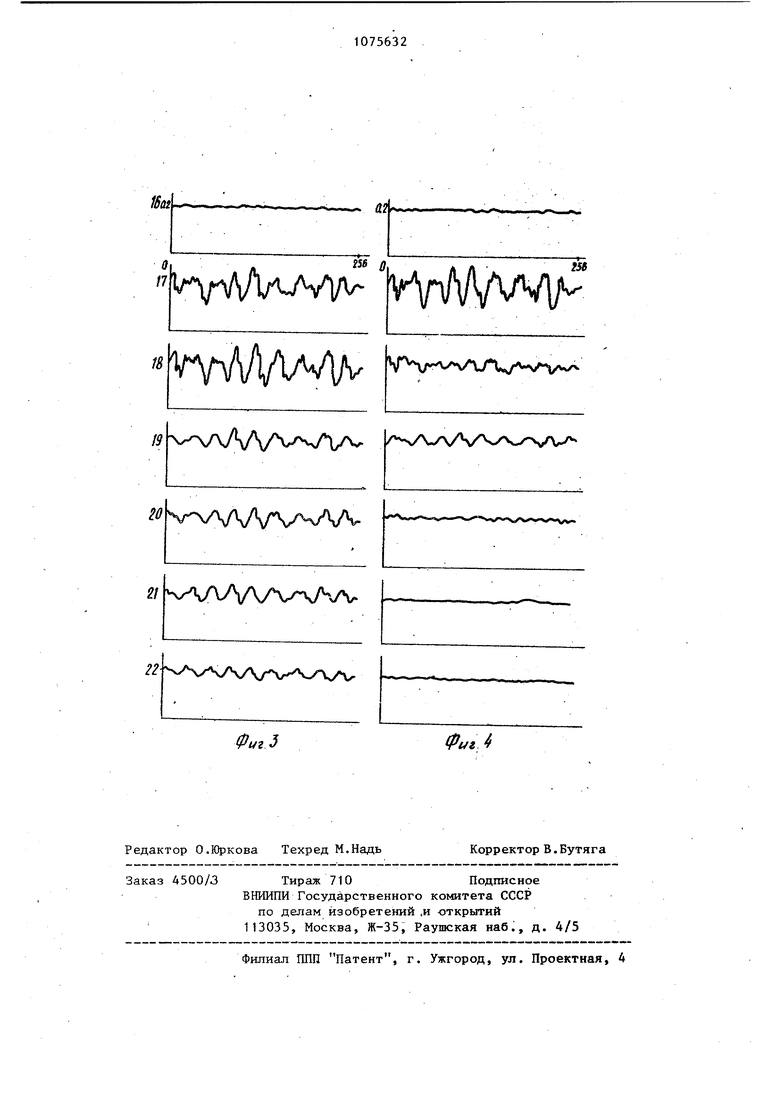
Таким образом, изменение мембранного потенциала за единичный квант времени, обусловленное пассивными и активными свойствами мембраны нейрона, а также приходящими на ней. 10 рон сигналами от внешнего источника и от нейронов моделируемой структуры, удовлетворяет еледующему разностному уравнению: РД Н)-РЛ С1)).(1) Многочисленные нейрофизиологические данные показьшают, что эффективность синаптической связи не является постоянной величиной, а изменяется сложным образом в зави симости от предшествукщей активности пресинаптического нейрона /. Эти данные указывают также на то, что эффективность синапса определяется двумя основными процессами, протекающими в пресинаптическом волокне: один из которых связан с регуляцией передатчика (медиатора) Xj-, , а другой связан с регуляцией, концентрации внутриклеточного кальция 1 Поскольку изменения синаптической эффективности в синапсах центральной нервной системы позвоночных составляют всего несколь ко процентов от среднего уровня, зависимость Уи( двух параметров Xj i2 быть достаточно точно описана с помощью линейных членов разложения в ряд Тейлора, т-е- y,-j(k) Xj(k;+ Xj.2 (kj, здесь постоянный член разложения и сомножи тели включены в х- и .Xjo. Изменение парамет-ров ii x-j за единичный интервал времени зависи значения и состояния нейронов в предшествующий момент времени, т.е. имеют место следующие уравнения:ji((j(1)(yk,N.(.)), х(Ы)-XJ.2(t)Ф,(x,Ck),)). Раскладьшая функции Ф,, РЯД Тейлора и ограничиваясь членами линейными по X и п (малость изменений Xj и Xj2 позволяет надеяться на хорошее соответствие этого линейного приближения экспериментальным данным), получаем следующие уравнения: Xj-,(1.M)-x.(1.)(k)Xj.(kK,N.CJcW) x,,,(4H)-x.( Щ C,N.ikh2, Коэффициенты в этих уравнениях имеют следующий физиологический смысл: (2) постоянная времени возвращения переменной Xj, к своему равно- : весному значениюопределяет вели- ; чину, на которую уменьшается количество доступного медиатора при срабатывании j-ro нейрона, . . здесь . i Следует отметить, что процесс регуляции медиатора приводит к истощению доступного медиатора при р итмической стимуляции нейрона и к соответствующему уменьшению постсинаптического потенциала - явлению синаптической депрессии. Сл - определяет величину, на которую увеличивается концентрация внутриклеточного кальция при срабатывании j-ro нейрона, здесь с 0. Процесс регуляции концентрации внутриклеточного кальция приводит к повышению концентрации кальция при ритмической стимуляции нейрона, что, в свою очередь, ведет к увеличенто вероятности освобождения медиатора и к увеличению постсинаптического потенциала - явление синаптической потенциации. Величины и и 2 определяют средний уровень концентрации медиатора и внутриклеточного кальция. Из системы уравнений, описывающих изменения Х; и x-j , нетрудно получить, что при скачкообразном изменении частоты разряда пресинаптического нейрона от F до f- , вы- .званные изменения синаптической эффективности могут быть представлены в виде суммы двух эксЬонент (при замене разностных уравнений диффе- ренциальными) с постоянными времени Н7(Л,Й,М и -1/(A2+B,,-F), что находится в хорошем согласии с экспериментальными данными. Выбор параметров /I, , А, , 6., , Bj , 0,0, D J БЗ осуществлялся на основе уравнений по методу наименьших квадратов. Устройство работает в различных режимах, задаваемых параметрами синаптической депрессии и потенциации. Параметры моделей .нейрона (порог, постоянная времени мембран амплитуда белого шума, характери зующего случайные синаптические воздействия на модели нейронов, несвязанные с сигналом, и моделиру щего спонтанную активность нейронов) , а также вид функции связи могут быть выбраны на основе нейро физиологических и психофизиологиче ких данных, полученных на человеке и животных, при этом можно считать что длительность каждого шага рабо ты устройства соответствует длител ности передачи сигнала в синапсе синаптической задержке, равной 0.5 мс. Рассмотрим следующие значе ния параметров модели нейрона: 0 0,15 е-1,0, белый шум - слу чайная величина, подаваемая на каж дом шаге на каждый нейрон, равноме но распределенная в интервале 0,20 0,26. Параметры внешнего сигнала, распределенного по моделям нейронов, представлены на графике 14 (фиг. 2), где абсцисс - номер модели нейрона по порядку, по оси ординат - величина внешнего сигнала, подаваемого на входы 2 соответствующей модели нейрона. Вид функции связи представлен на графике 15s где по оси абсцисс модуль разности .порядковых номеров взаимодействующих моделей нейронов по оси ординат - сила связи между этими моделями. Параметры синаптической пластичности также выбирают на основе нер1рофизиологических данньЕХ, при этом рассмотрим два типа синапсов: с преобладанием синаптической потенциации (т.е. си напсы, длительная стимуляция котор в конечном счете приводит к увеличению синаптической эффективности) И с преобладанием синаптической депрессии (т.е. синапсы, длительная стимуляция которых приводит к уменьшению скнаптнческой эффекТ11ВНОСТИ) , На фиг. 3 сверху вниз изображены последовательные этапы работы устройства со следующими параметра ми синаптической пластичности, соответствующими преобладанию процес са синаптической потенциации: Л, - О, Bi 0,25, С, 0,12-5, D-, 0,026, А2- О, б2--0,05, ,,1, ,0095. На каждом графике, представляющем результат усреднения по 64 последовательным шагам работы устройства и пяти различным реализациям, определяемым исходными начальными состояниями, по обе оси абсцисс отложены номера моделей нейронов в слое, по оси ординат - частота срабатывания модели нейрона. Представлены следующие этапы работы устройства: 16 - на внешние входы устройства подается случайный сигнал (белый шум), моделирующий спонтанную активность нейронов слоя, 17 и 18 - на внешние входы устройства наряду с белым .шумом поступает определенный пространственно распределенный внешний сигнал, представленный на графике 14, 19, 20, 21 - последовательные этапы работы устройства после выключения стимула, 22 - через 512 шагов после выключения стимула. Из фиг. 3 отчетливо видно, что рассматриваемое устройство осуществляет фильтрацию низкочастотной пространственной составляющей внешнего сигнала, причем след от сигнала сохраняется в течение достаточно длительного времени, значительно превьш1ающего характерное время потенциации, для данного случая составляющее 100 шагов. Таким образом, в случае преобладания процесса синаптической потенциации устройство проявляет свойство кратковременной памяти, т.е. может в течение достаточно длительного времени, превосходящего по продолжительности временные параметры синаптической пластичности одиночной модели нейрона, удерживать след внешнего сигнала. На фиг, 4 сверху вниз представлены последовательные этапы работы устройства со следующими параметрами синаптической пластичности, соответствующими преобладанию процесса синаптической депрессии: , 8, -0,05, Ст О, D 0,0095, 2 0, ,25, С,, 0,375, ,026. Обозначения те же, как и на фиг. 3. Из приведенных графиков видно, что реакция устройства на внешний сигнал уменьшается с течением времени привыкание. После выключения внешнего сигнала наблюдается интересное явление отдачи, характеризующееся реакцией устройства, инверсированной к исходной реакции на
внешний сигнал. Это свойство наблюдается в нейронных популяциях мозга человека и животных - возбуткдение на включение стимула, торможение на выключение, и наоборот. После 5 этой непродолжительной отдачи устройство возвращается в исходное состояние. Следовательно,в случае преобладания процесса .синаптической депрессии устройство обладает свойством примыка- |Q ния к действующему внешиему сигналу.
Таким образом, введение в модель нейрона двух интеграторов, двух умножителей и сумматора, обеспечивающих изменение величины рвязи между нейронами в зависимости ot частоты срабатывания пресииаптического нейрона и достаточно полно опис 1ш1ающих процессы синаптической депрессии и потенциации, позволяет смоделировать свойства реальных нейронных структур, а именно привыкание и кратковременную память, и приблизить поведение тфедлагаемого устройства к реальной картине.




| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для моделирования нейрона | 1989 |
|
SU1709356A1 |
| Способ моделирования активности головного мозга пациента с эпилепсией | 2024 |
|
RU2841470C1 |
| НЕЙРОИМИТАТОР | 1993 |
|
RU2074414C1 |
| УСТРОЙСТВО ДЛЯ МОДЕЛИРОВАНИЯ НЕЙРОНА | 1991 |
|
RU2028669C1 |
| Устройство для моделирования нейрона | 1987 |
|
SU1501101A1 |
| УСТРОЙСТВО ДЛЯ МОДЕЛИРОВАНИЯ НЕЙРОНА | 1991 |
|
RU2029368C1 |
| УСТРОЙСТВО ДЛЯ МОДЕЛИРОВАНИЯ САМООРГАНИЗУЮЩИХСЯ СЕТЕЙ НЕФОРМАЛЬНЫХ НЕЙРОНОВ | 2011 |
|
RU2484527C1 |
| Модель адаптивного нейрона | 1978 |
|
SU765823A1 |
| ИМПУЛЬСНЫЙ НЕЙРОН, БЛИЗКИЙ К РЕАЛЬНОМУ | 2015 |
|
RU2598298C2 |
| Устройство для моделирования нейрона | 1987 |
|
SU1439631A1 |

УСТРОЙСТВО ДЛЯ МОДЕЛИРОВАНИЯ НЕЙРОНА, содержащее цифровой интегратор, прямые входы которого являются входами возбуждения устройства, и цифровые интеграторы потенциации и депрессии, выходы которых подключены к соответствующим входам сумматора, отличающееся тем, что, с целью повышения точности моделирования и упрощения конструкции, в него введены два блока умножения и компаратор, выход которого подключен к первым входам-цифровых интеграторов потенциации и депрессии и блоков умножения, выходы ци.фровых интеграторов потенциации и депрессии соединены с вторыми своими входами и с вторыми входами соответствующих блоков умножения, выходы которых подключены к третьим входам соответствующих цифровых интеграторов пoтeн J aции и депрессии, четвертые входы цифровых интеграторов потенциации и депрессии соединены с источниками постоянного (Л сигнала, выход цифрового интегратора подключен к первому инверсному входу цифрового интегратора, второй инверсный вход которого соединен .с выходом компаратора, выходом устройства является выход сумматора. | ел Од оо IsD
JJ
«
«.
15
n/V /lAjVl/v
/7
НЛАДМАIK
kx AA/ /VX/VV
IS
КглЛДЛЛ/ АА20
KAAAA/WHA
21
uzJ
fSГSr AУX/v лv
iput 4
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Позин Н.В, Моделирование нейронных структур, М., Наука, 1970, с | |||
| Арматура для железобетонных свай и стоек | 1916 |
|
SU259A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Устройство для моделирования нейрона | 1978 |
|
SU767788A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1985-06-30—Публикация
1982-05-25—Подача