Изобретение относится к автоматике и вычислительной технике и может быть использовано для нелинейных преобразований мгновенных значений сигналов.
Известны функциональные преобразователи, в которых заданные функции аппроксимируют полиномами Чебьгшева р
Однако при увеличении количества членов ряда аппаратурная погрешность резко возрастает.
Наиболее близким к предлагаемому является функциональный преобразователь содержащий п сумматоров и п множительных блоков, в котором степенной ряд независимой переменной воспроизводится при помощи последовательно соединенных множительных блоков и сумматоров L2 J.
Недостатками этого устройства являются сложность расчета и настройки коэффициентов и невозможность воспроизведения полиномов с произвольными коэффициентами. При этом коэффициенты полиномов, воспроизводимых при помощи этого устройства, являются взаимосвязаннь1ми, что ограничивает точность аппроксимации.
Цель изобретения,- повышение точности и упрощение программирования преобразователя.
Поставленная цель достигается тем, что функцио1 альный преобразователь,, содержащий п сумматоров и п множительных блоков, выход каждого i-ro из которых соединен с первым входом i-ro сумматора, выход каждого i-ro сумматора, кроме первого, соединен с первым входом (i-1)-ro множительного блока, выход первого сумматора и первый вход п-го множительного блока являются соответственно выходом и информационным входом преобразователя, содержит инвертор, вход которого является входом задания первого коэффициента разложения функции по полиномам Чебышева, а выход подключен ко второму входу первого сумматора, вторые входы с первого по (п-1)-й множительных блоков содинены с информационным входом преобразователя, вторые входь со второго по п-й сумматоров являются входами задания со второго по п-й коэффициентов разложения функции по полиномам Чебышева, второй вход п-го множительного блока соединен с третьим входом (п-1)-го сумматора и является входом задания (п+1)-го коэффициента разложения функции по по.пиномам ЧебьЕиева, выход каждого i-ro сумматора, начиная с третьего, подклк1чен к третьему входу (i-2)-ro сумматора,
Повышегсие порядка аппроксимации достигае| ся в преобразователе последовательным применением операций суммирования и умножения на независимую переменно, причем коэффициенты сумматоров выбраны таким образом, что на их входы подаются напряжения, пропор,циональные коэффициентам Чебышевского разложения воспроизводимой функт ции, что позволяет избежать операции пересчета коэффициентов, необходимой при использовании устройства-прототипа, и тем самым упростить программирование. Кроме того5 при воспроизведении гладких функций КОЭффИЦИ12НТЫ
разложения в ряд по полиномам 1ебь шева бьстро убываютS поэтому влияние аппаратурных погрешностей ка;кдог(з последующего множительного блока и сумматора тоже быстро уменьшается и общая погрешность определяется; в основном, точностью одного-двух пе1)вых блоков,, что позволяет повысить ::очность устройства. Пониженные требования к точности блоков, реализующргх старшие члень5 ряда, начиная с трбтьего, позволяют использо,вать ,для цели сравнительно неточные дешевые элементы и снизить стоимость устройства.
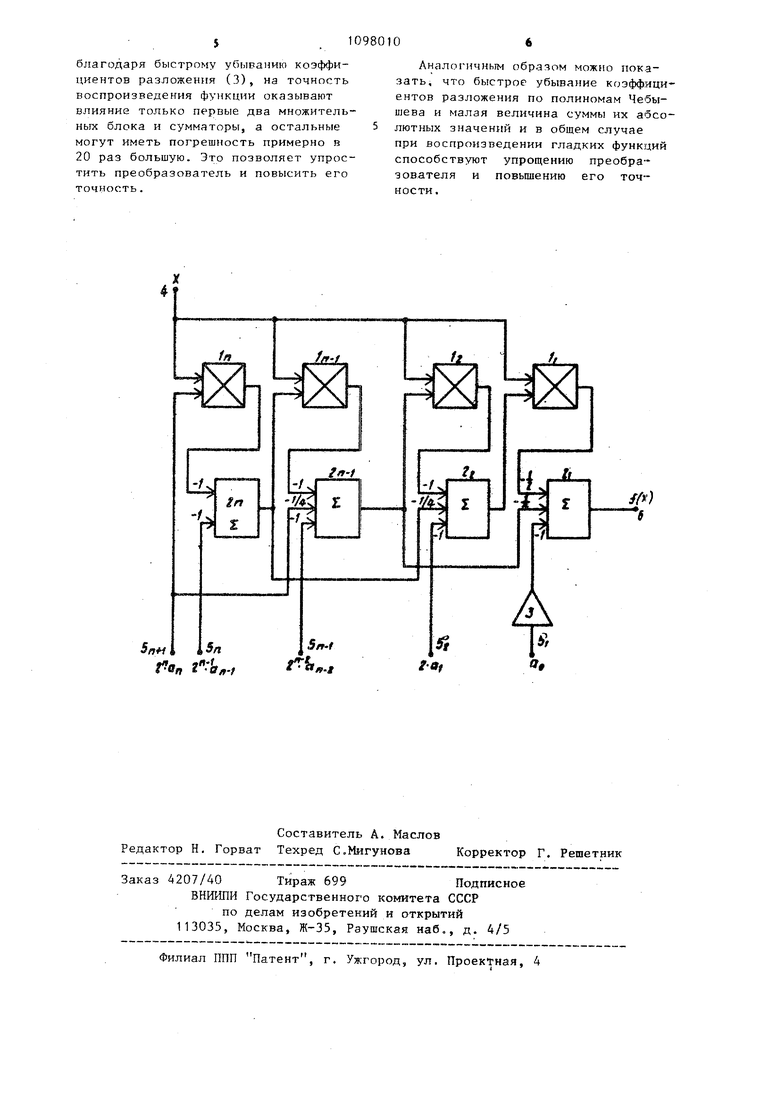
На чертеже показана блок-схема преобразователя.
Преобразователь содержит п множительных блоков (-|, п Cyt-iMaTOpOB
, инвертор 3, информационный вход 4, входы 5,--5 1 задания коэффициентов разложения функций в ряд, выход 6 преобразователя.
Преобразователь работает следующим образом.
Входной сигнал х поступает на информационный йкод 4 S, а на входы пода;«тся сигналы, пропорциональные коэффициентам разложения воспроизводимой фу 1кции f(x) по полиномам Чебышева. Вход 4 соединен с первым входом п-го множительного бло5:а l.p и вторыми входами остальных MHCIжнтельных блоков Ь-Ц. Выход кглздого 1-го множительного блока 1 соединен с первым входом соответствующего 1-го сумматора 2-, второй вход каждого i-ro сумматора 2 j соединен с i-Mo входом 5; п1Ьеобраэователя5 а выход первого сумматора 2-, является вьгхо310дом 6 преобразователя, выход каждого i-ro из остальных сумматоров 22-2 соединен с первым входом (i-l)-ro множительного блока 1. , третьи вхо ды i-x сумматоров, кроме п-го и (n-l)-ro, соединены с выходом (i+2)сумматора, а третий вход (п-1)-го сумматора 2| соединен со вторым входом п-го множительного блока 1 и с (п+1)-м входом 5„ преобразователя.. При этом на вход п-го множительного блока 1 f, поступает входной сигнал X и сигнал, пропорциональный п-му коэффициенту разложения, их про изведение суммируется сумматором 2, с сигналом, пропорциональным (п-1)-м коэффициенту разложения. Выходной сигнал сумматора 2, умноженный при помощи (п-1)-го множительного блока 1 на независимую переменную, пает на вход сумматора 2 f, совместно с сигналами, соответствующими п-му и (п-2)-му коэффициентам разложения, поступающими соответственно На входы каждо на входы 5 го i-ro из остальных сумматоров 5Iпоступают выходной сигнал (i+1)-ro сумматора, умноженный на входной сигнал X, сигнал с i-ro входз 5., пропорциональный (i-l)-My коэффициенту разложения и выходной сигнал (i-2)-ro сумматора, причем сигнал с 1-го входа 5 предварительно инверти руется инвертором 3. При соответствую щем выборе мзсштабньпс коэффициентов на выходе 6 преобразователя можно по лучить функцию f(x), коэффициенты ра ложения которой по полиномам Чебышев до п-го члена включительно совпадают, с учетом соответствующих масштаб ных коэффициентов, с сигналами, пода Баемыми на входы 5| преобразователя. Рассмотрим конкретный пример одно го из возможных способов масштабирования преобразователя для случая , предполагая, что все сигналы представлены в виде напряжений. Обо значив выходное напряжение i-ro сум матора через U , а входные напряжений, подаваемые на i-й вход 5.-. через 2 сн TtOnOQ Уrj .ГГЛЛП 7ТТЫ1 Л получим: посту 0 Исключая из системы уравнент (1) переменные U, U , U И U, получим: f(x).«.o x+a {l-2xZ)c(fx3-3xkc,Jl-8x 8x j,.(2j f(x),+a,T +3212+33X3+3 1, где символзми Tj, как обычно, обозначены полиномы Чебытевз i-й степени. Работоспособность преобрззовзтеля для малых п() легко проверяется непосредственно, з для больших п ее можно Докззать методом матемзтической индукции. Как обычно, HcnojfbsyH замену переY 3Z X 2 менных при помощи данного преобразователя можно воспроизводить также функции, представленные в виде разложения по смещенным полиномам Чебьппева Т Функциональный преобразователь позволяет производить набор произвольных функций непосредственно по известным коэффициентам разложения по полиномам Чебьпиева. Так, например, для функции заданной из отрезке f-l, 1j известно разложе.ние С.,47200-0,49940Т (х1+002799Т (х) (з) Z2 ; | которое имеет погрешность на более 0,06%. Коэффициенты разложения (3), равные соответственно ,47200, , ,49940, , а 0,02799 могут быть введены непосредственно на входы 5 функционального преобразователя (с точностью до постоянных множителей, кратных степеням числа 2), что значительно упрощает программирование функционального преобразователя. Из разложения (3) видно, что сумма абсолютных значений коэффициентов не превосходит максимального значения воспроизводимой функции, т.е. единить Благодаря этому влияние погрешности установки коэффицинтов на погрешность воспроизведения функции минимально. Кроме того.
благодаря быстрому убыванию коэффициентов разложения (3), на точность воспроизведения функции оказывают влияние только первые два множительных блока и сумматоры, а остальные могут иметь погрешность примерно в 20 раз большую. Это позволяет упростить преобразователь и повысить его точность.
Аналогичным образом можно показать, что быстрое убывание коэффициентов разложения по полиномам Чебышева и малая величина суммы их абсолютных значений и в общем случае при воспроизведении гладких функций способствуют упрощению преобразователя и повышению его точности.

| название | год | авторы | номер документа |
|---|---|---|---|
| Функциональный преобразователь | 1983 |
|
SU1142846A1 |
| Устройство для воспроизведения дробно-рациональных функций | 1983 |
|
SU1151999A1 |
| Функциональный преобразователь | 1981 |
|
SU993284A1 |
| Функциональный преобразователь | 1983 |
|
SU1156099A1 |
| Генератор ортогональных полиномов | 1979 |
|
SU773651A1 |
| Гибридный функциональный цифроаналоговый преобразователь со сплайновой аппроксимацией n-го порядка | 2016 |
|
RU2628918C1 |
| Частотно-импульсный функциональныйпРЕОбРАзОВАТЕль | 1979 |
|
SU842854A1 |
| Экстраполятор | 1990 |
|
SU1837317A1 |
| Функциональный декодирующий преобразователь | 1976 |
|
SU696489A1 |
| Функциональный генератор | 1979 |
|
SU781839A1 |

ФУНЮДИОНАЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ, содержащий п сумматоров и п множительных блоков, выход каждого i-ro из которых соединен с первым входом i-ro сумматора, выход каждого i-ro сумматора, кроме первого, соединен с первым входом (i-l)-ro множительного блока, выход первого сумматора и первый вход п-го множительного блока являются соответственно выходом и информационным входом преобразователя, отличающийся тем, что, с целью повьппения точности и упрощения программирования преобразователя, он содержит инвертор, вход которого является входом задания первого коэффициента разложения функции по полиномам Чебышева, а выход подключен ко второму входу первого сумматора, вторые входы с первого по (п-1)-й множительных блоков соединены с информационным входом преобразователя, вторые входы со второго по п-й сумматоров являются входами задания со второго по п-й коэффициентов разложения функции по полиномйм Чебышева,- второй вход п-го множи(Л тельного блока соединен с третьим входом (n-l)-ro сумматора и является входом задания (п+1)-го коэффициента разложения функции по полиномам .Чебьшева, выход каждого 1-го сумматора, начиная с третьего, подключен i к третьему входу (i-2)-ro сумматора. со 00
Авторы
Даты
1984-06-15—Публикация
1983-03-01—Подача