Изобретение относится к вычислительной технике и может найти применение при статистическим моделировании на аналоговых вычислительных машинах, а также при создании аппаратуры для формирования случайных процессов. Известно устройство для формирования марковских процессов, содержардее источник нормального белого шума, блок суммирования, блок нелинейного преобразователя и блок интег рирования Cl J. Недостатком данного устройства является невозможность формирования случайных процессов, имеющих заданньш закон распределения и корреляционную функцию, отличную oт экспоненциальной. Наиболее близким к изобретению техническим решением является генера тор случайных процессов, содержащий источник нормального белового шума, блок перемножения, Ьлок суммирования, блок интегрирования, блок нелинейности типа зона нечувствительности, блок нелинейности типа ограничение, блок вычитания, блок нелинейного преобразования, два блока извлечения квадратного корня, источник постоянного напряжения, коммута тор и масштабный усилитель, при этом выход источника нормального белого шума соединен с первых входом блока перемножения, выход которого подключен к первому входу блока суммирования, выход которого покдлючен к входу блока интегрирования, выход которого соединен с входом нелинейного блока типа зона нечувствительности и входом нелинейного блока типа ограничение, выходы которых подключены соответственно к первому и второму входам блока вычитания выход которого, являющийся выходом устройства в целом, соединен с входом блока линейного преобразования и входами первого и второго нелинейных блоков извлечения квадратного корня, выходы которых и выход источника постоянного напряжения подключены соответственно к первому, второму и третьему входам коммутатора, выход которого соединен с входом масштабного усилителя, выход которого соединен с вторым входом блока перемножения, второй вход блока суммирования соединен с выходом блока линейного преобразователя 2 Недостатком известного устройства является невозможность обеспечения взаимной независимости одномерной плотности распределения формируемого случайного процесса и его корреляционной функции. Целью изобретения является расширение функциональных возможностей путем обеспечения взаимной независимости одномерной плотности распределения случайного процесса и его корреляционной функции. Для достижения поставленной цели в генератор случайных процессов, содержащий источник шума, первый усилитель, первый сумматор, первый интегратор, первый линейный преобразователь, коммутатор, введены переключатель, три усилителя, три нелинейных преобразователя, второй сумматор, второй интегратор и второй линейный преобразователь, выход которого соединен с входами первого второго и третьего нелинейных преобразователей, выходы которых соединены соответственно с первым, вторым и третьим входами коммутатора, выход которого соединен с входом первого линейного преобразователя, выход которого является выходом генератора, выход источника шума соединен с входами первого и второго усилителей, выходы которых соединены соответственно с первыми входами первого и второго сумматоров, выход третьего усилителя соединен с вторым входом второго сумматора, выход первого сумматора соединен с первым входом переключателя, выход которого через первый интегратор соединен с входами второго линейного преобразователя и четвертого усилителя, выход которого соединен с третьим входом второго сумматора, выход которого через второй интегратор соединен с вторыми входами первого, сумматора и переключателя и с входом третьего усилителя. Для пояснения сущности изобретения рассмотрим теоретические основы формирования непрерывного стационарного случайного процесса Z(t) с заданными одномерной плотностью распределения uJ(Z) и корреляционной функцией ). Как известно, большинство распространенных непрерывных одномерных плотностей распределения U)(Z)
относится к S-распределениям Джонсона. При этом аналитически плотности S-распределений можно выразить:
р{-|- уп п
z + )
(Я
, , е)ср -llyng
-w :-)л I Н
fc
)П,
(2) где h , Л , Т и - параметры. Выражение (1) соответствует S-распределению Джонсона, выражение (2) - S -распределению Джонсона, выражение (3) - 8ц-распределеншо Джонсона. Выбор подходящего S-pacпределения Джонсона зависит от вели чин квадрата коэффициента ассиметри /), М§ /Mi и коэффициента эксцесса (5) 2
желаемого стационарного случайного процесса Z(t), подчиненного одномерной плотности распределения U)(Z) В выражениях (4) и (5) Mj ,- второй центральный момент (дисперсия) процесса Z(t), Mj и Мц. - соответственно третий и четвертый центральный моменты процесса Z(t).
Таким образом, для построения Sраспределения Джонсона, соответствующего заданной плотности распределения u)(Z), необходимо рассчитать по формулам (4) и (5) квадрат коэффициента ассиметрии /ь и коэффициент эксцесса , характеризующие заданную плотность распределения Uj(Z) , .При этом формула для вьгчисления моментов Mj - М. имеет вид
М; (Z - т.) и; (Z)dZ, i S , 4, ..., га Г Z uj(Z)dZ.
Дпя некоторых плотностей распределения коэффициенты р, и р указаны в справочной литературе.
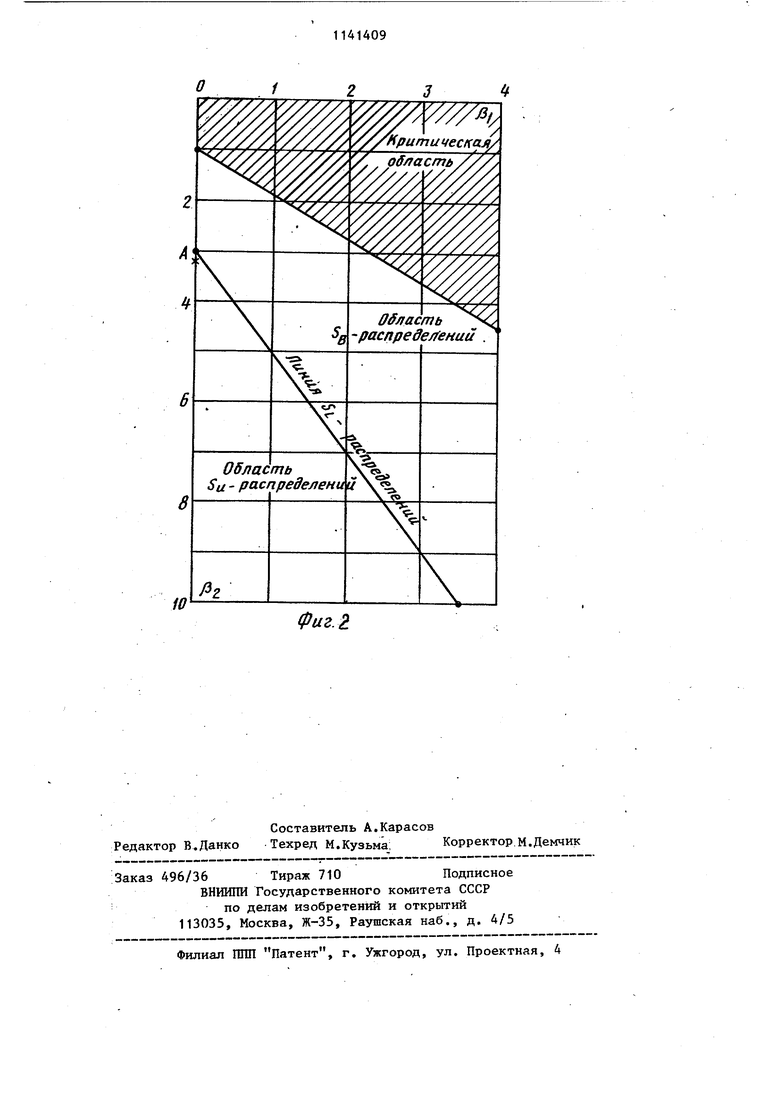
Затем с помощью Лиг. 2 по рассчитанным р и fti определяютвид подходящего для заданной и) (Z) S-pacnpeделения.
Далее рассчитывают параметры iv f f к Е выбранного S-распределения, используя метод моментов или условие минимума функционала, характеризующего различие заданного и выбранного распределений, например функционала вида
.i()
или
если Z(t) имеет плотность распределения , (2) ,
zct);iexp(2M:IL). , сэ)
если Z(t) имеет плотность распределения (3) .
Из выражений (7) - (9) видно, что алгоритм формирования каждого S-распределения один и тот же.
Сначала нормированный гауссовский процесс y(t) линейно преобразуют с целью получения процесса
(
Сю)
затем полученный процесс ) подвергают нелинейному преобразованию вида
V -N(tl--ll P illl- f-,i
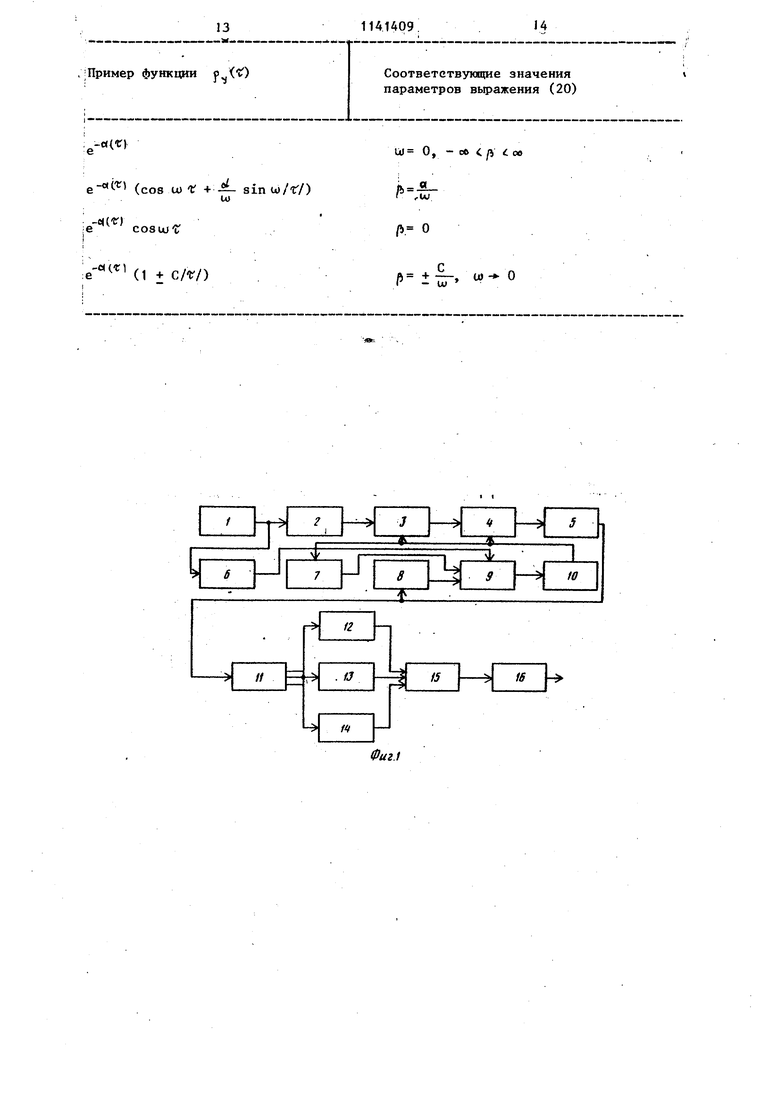
.p(.(tl) . ,х|и)(г|-.(2д,Л,т.)| , je(V.3). (ь) Процесс Z(t), имеющий одно из S-распределений (1) - (3), может быть представлен как результат нелинейного преобразования Джонсона некоторого нормального (гауссовского) нормированного процесса v(t): rv(i|-J- 1 1.e. если Z(t) имеет плотность распреде- i,Z(t) ления (1), z(t,4..«f(iui).E;(., или вида 2(И())s1,(:((t|)±exp(y(i|)Лexp{-/(4 или вида (W)exp(,(t)) в зависимости от вида S-распределения. Далее результат нелинейного преобразования подвергают линейному преобразованию с целью получения процесса z(t). (3(t))fe , re(i,2,3) , (н) имеющего требуемое S-распределение Для того, чтобы процесс Z(t) имел заданную корреляционную функци .. ), необходимо соответствующим образом выбрать нормированную корре ляционную функцию fy () вспомогательного процесса y(t). Указанньй выбор может быть осу1чествлен в два этапа. На первом этапе вспомогательный процесс y(t) выражается явным образом через нелаемый процесс Z(t) с помощью выражений (7) - (10). Про делав необходимые преобразования, получают: (Ке.(т4|)гг , («1 Z(t) имеет плотность распределения (1), ,(.y) , (1Ы если Z(t) имеет плотность распреде ления (2), :,(ti,e,-mii.y . П) если Z(t) имеет плотность распреде ления (3). На втором этапе по известной кор реляционной функции K2(t) и по виду преобразований (15) - (17) определяют искомую нормированную корреляционную функцию ,,() по формул .jecw) (19 /J () - правая часть вьфажений (15) - (17), причем при j 1 следует брать правую часть выражения (15) и т.д., ( - среднеквадратическое отклонение процесса Z(t) Hj(Z) - полином Эрмита п-го порядка, f(,Z) - нормированная корреляционная функция процесса Z(t). При практическом проведении расчетов в ряду (18) нужно оставлять лишь несколько первых членов. Это число N может быть получено из условияN I XcJ/n , которое получается из формулы (18) при Т 0. В результате случайный процесс Z(t) . имеющий желаемые одномерную плотность распределения ы.Х и корреляционную функцию ) , может быть сформирован путем последовательных преобразований (10), (11) или (12), или (13) и (14) нормированного гауссовского случайного процесса y(t), имеющего (нормированную) корреляционную функцию f,(T). Рассмотрим формирование нормированного гауссовского случайного процесса y(t) с корреляционной функцией (). При этом ограничимся рассмотрением лишь таких р (г), которые описываются выражением j)(()U|j , (2в) где а , U) и - параметры. В таблице приведено несколько наиболее часто встречающихся функций семейства (20). Можно показать, что гауссовский случайный процесс y(t) с корреляционной функцией вида (20) может быть сформирован как компонента у (t) вумерного марковского процесса , .1 порождаемого следующей сиса tV.. темой стохастических дифференциальных ЗФавнений: U) 2(t)tfe(i) ) ))2( . 7. где f(t) - ста1р онарный белый шум, т.е. гауссов белый шум с. нулевым математическим ожиданием и корреля ционной функцией К с {т) ), дельта-функ1щя Дирака, -(а + 10), (22) 22 . Ь, l2(a -Л (Ч))) ( ), bj I2(a )(а2 + u) - 2ab . Таким образом, y(t) у (t) .При этом нужно помнить, что случайный процесс у(t) (и, следовательно, случайный процесс y(t) будет иметь корреляционную функцию (20) после установления его стационарности. Окончательно получаем, что для сформирования случайного процесса Z(t) с заданной одномерной плотностью распределения и}(2)и заданной корреляционной функцией К2( ) необходимо сформировать двумерный гауссовский случайный процесс удовлетворяющий системе дифференциальных сравнений (22), компоненту у этого процесса подвергнуть линейному преобразованию вида (10), результат которого подвергнуть одному из трех нелинейных преобразований вида (11) - (13), а результат последнего преобразования подвергнуть линейному преобразованию вида (14). При этом параметры i , Л , j и линейных (10) и (14) и одного из нелинейных (11) - (13) преобразований, параметры а , ц) и (S функции (20 и коэффшщенты ад, 2i i системы дифференциальных уравнений (21) рассчитываются заранее. В качестве примера использования предлагаемого подхода рассмотрим формирование случайного процесса Z(t) с плотностью распределения вид u)(Z) exp(Z/0,165); fO,165 t + + exp(Z/0,165) (23) и корреляционной функции вида K2(O 0,09 exp(-2 /r/)(1 + + 0,45 /r/).(24) Плотность (24) называется логисти кой. Известно, что математическое 9 ожидание т, дисперсия (jf , квадрат коэффициента, ассиметрии / и коэффициент эксцесса процесса Z(t), подчиненного плотности (23), имеют следуюпще значения: т О, Mj 62 0,09, р, О, ,ь, 4,2. Точка А с координатами (0,4.2), вид видно из фиг. 2, находится в области Sy-распределений Джонсона, следовательно, плотность распределения (23) может быть представлена как плотность S -распределения Джонсона, т.е. вида: (2). Выберем параметры плотности (2). Прежде всего заметим, что в силу центрированности (т 0) и симметричности ( Pi 0) плотности (23) необходцмо, чтобы параметры f и плотности (2) равнялись нулю. Оставшиеся параметры и Л плотности (2) выберем из условия минимума функционала (6) с учетом равенства и(0) f, (О, г , Л ). Проделав необходимые вычисление, получим а 1,937, Л 0,510. Таким образом, преобразование, которому следует подвергнуть вспомогательный нормированный гауссовский процесс y(t) для получения процесса Z(t) с вероятностными характеристиками (23) и (24), имеет вид (см. вьфажения (14) и (12) F(y(t) 0,5/ V,(ii) следовательно Z(t) 0,5/S1.., (25) Нормированная корреляционная функция у,, (С) процесса y(v) рассчитывается по формулам (18) и (19). При этом ra(62Z) 1,937 arcsh (-|) , p (O exp(-2/r/)(1+0,45 /f/). При практических расчетах в выражение (18) подставляют значения f() функции р(), причем i О, 1, 2, ..., 60, 1Г О, t-g 15. Интегралы в вьфажении (19) вычисляют численно. В результате получают таблицу значений р ( ) функции р ( Г ) , i 0, 1,2, ..., 60. Найденные зна чения аппроксимировались выражени ем (20), Хорошая точность аппроксимации достигнута минимизацией функ ционала Ol«m«;jc° (cosa)f.+sinu)|t,.|)-5)(i)) i IJ - . ПО параметрам а , ш и /г , в резул тате которой получено 0 1.6,ш 0, /i - произвольно. При указанных значениях о ,и) и /6, во-первых, нормированная корреля ционная функ1шя f М имеет вид , .сам а, во-вторых,-, коэффициенты (22) сис темы стохастических дифференциальных уравнений (21) принимают следую щие 3 нач е ния: -2.56, а22 -3.2, Ь 1.789, bj -2.862. Следовательно, после установления стационарности компонента у двумерного гауссовского случайного процесса ( О, порождаемого систеМОЙ стохастических дифференциальных уравнений типа (21), т.е. У, (t) y2(t) + 1,789 It), j(t} -2,56 y(t) - 3,2 y2(t)- 2,862pt), , имеет корреляционную функцию (26). Подвергнув сформированный таким спо собом случайный процесс- у (t) преобразованию (25) , получим случайный процесс Z(t) с желаемыми вероят-.костными характеристиками (23) и (24). При формировании случайного процесса предлагаемое устройство обеспечивает взаимную независимость его одномерной плотности распределения и корреляционной функции. На фиг. 1 представлена функциональная схема генератора, на фиг.2плоскость и /bj и ее области, соответствующие S-распределениям Джонсона с Генератор содержит источник 1 шума, первьй усилитель 2, первый сумматор 3, переключатель 4, первый интегратор 5, второй 6, третий 7 и четвертьА 8 усилители, второй сумма тор 9, второй интегратор 10, второй линейньш преобразователь 11, первый 12, второй 13 и третий 14 нелинейные преобразователи, коммутатор 15 и первый линейный преобразователь 16. Источник 1 шума в каядый момент времени t формирует нормальный белый шум единичной интенсивности (т.е. стандартный белый шум), который подается на первый усилитель 2 с коэффициентом усиления, равным Ц (см. систему дифференциальных уравнений (21). Выходной сигнал с первого усилителя 2 поступает на первый сумматор 3, где суммируется с сигналом, поступающим с выхода второго интегра. тора 10 и равным yj (см. систему дифференциальных уравнений (21)). Выходной сигнал с первого сумматора 3 поступает на первый вход переключателя 4, который может находиться в одном из двух состояний. В первом состоянии переключатель 4 соединяет выход первого сумматора 3 с входом первого интегратора 5, во втором - выход второго интегратора 10 с входом первого интегратора 5. В первом случае на вход первого интегратора 5 поступает сигнал, равный у (t) + b(t) и представляющий собой в соответствии с первым уравнением системы (21) производную сигнала y(t), т.е. у (t). В первом интеграторе 5 происходит интегрирование сигнала, равного у (t), в результате чего на выходе интегратора 5 формируется сигнал, равный у (t), т.е. нормированный нормальный процесс, имеюпщй после установления стационарного состояния корреляционную функцию вида (20). Указанный сигнал поступает-на вход линейного преобразователя 11 и на вход четвертого усилителя 8, который по техническому решению эквивалентен первому усилителю 2 и имеет коэффициент усиления, равный а (см. систему дифференциальных уравнений (21)). Выходной сигнал с четвертого усилителя 8 поступает на первый вход второго сумматора 9, где суммируется с выходным сигналом с третьего усилителя 7 и с выходным сигналом со второго усилителя 6. При этом сигнал с выхода третьего усилителя 7 представляет собой усштенньй ъ & раз сигнал с выхода второго интегратора 10, а сигнал с выхода второго усилятеля 6 представляет собой усиленный в bj раз нормальный белый шум, сформированный источником 1 шума. Второй.6 и третий 7 усилители по техническому решению эквивалентны первому усилителю 2 и имеют коэффИциенты усиления Ь и а j соответственно. В результате на выходе второго сумматора 9, который по тех ническому решению представляет собо операционный усилитель, например, с рии К140, К153 и т.п., создается сигнал, равный агУг + bjfCt) и являющийся в соответствии со вторым уравнением системы (21) производной сигнала y(t), т.е. yjCt). Во втором интеграторе 10, который по техническому решению эквивалентен первому интегратору 5, происходит интегрирование сигнала, равного yjCt), в результате чего на выходЛ интегратора 10 создается сигнал, равный у(t) и необходимый для формирования сигнала y(t). Таким образом, в блоках 1-10 формируется сигнал y,(t), который вместе с сигналом ) образует решение системы стохастических дифференциал ных уравнений (21). В том случае, когда переключател 4 находится во втором состоянии (т.е. соединяет выход второго интегратора 10 с входом первого интегратора 5), .сигнал -у2 Р выхода второго интегратора 10 поступает непосредственно на вход первого интегратора 5, где происходит его интегрирование. Данньй случай позволяет формировать такие случайные процессы у (t), которые являются CO тавной частью решения системы дифференциальных уравнений (21), когда в последней Ъ., 0. Это соответствует, например, ситуации, когда корреляционная функция процесса р (т) должна иметь вид fs,t) ()(t|. Вне зависимости от состояния переключателя 4 выходной процесс y(t) с первого интегратора 5 посту пает на вход второго линейного пре- образователя 11, в котором осуществляется преобразование (10), т.е. формируется сигнал y(t) y,(t) - ff / n, Линейный преобразователь 11 может быть выполнен в виде аналогового линейного функционального преобРазователяСигнал y(t) с выхода линейного преобразователя 11 поступает одновременно на входы первого 12, второго 13 и третьего 14 нелинейных преобразователей, в которых осуществляются преобразования (11) - (13) соответственно. Нелинейные преобразовятелк 12-14 могут быть выполнены в виде нелинейных функциональных преобразователей Аналоговые блоки таких преобразователей также хорошо известны СЗ. Выходные сигналы с нелинейных преобразователей поступают соответственно на первый, второй и третий входы коммутатора 15. Коммутатор 15 в зависимости от своего состояния.соединяет выход одного из трех нелинейных преобразователей 12-14 с входом линейного преобразо еля 16, в котором осуществляется преобразование (14), т.е. формируется сигнал ZCt)V. ()+E , je(l,2,3) , где V- (y(t) - сигнал с выходя одного из трех нелинейных преобразователей. Сигнал Z(t) на выходе линейного преобразователя 16 является искомым случайным процессом, так как имеет желаемые заранее заданные одномерную плотность распределения ui(Z) и корреляционную функцию K2(f). Возможность создания устройства для формирования процесса с произвольными одномерной плотностью распределения и корреляхщонной функцией, задаваемыми независимо друг от друга, расширяет функциональные возможности предлагаемого устройства и сферу его применения.
;пример функции )
Соответствующие значения параметров выражения (20)





| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для моделирования случайных процессов | 1973 |
|
SU452841A1 |
| ЦИФРОВАЯ СИСТЕМА СЕЛЕКЦИИ ДВИЖУЩИХСЯ ЦЕЛЕЙ | 1995 |
|
RU2087006C1 |
| УСТРОЙСТВО АДАПТИВНОГО ОЦЕНИВАНИЯ СОСРЕДОТОЧЕННОЙ ПОМЕХИ | 2008 |
|
RU2381620C1 |
| Устройство передачи и приема информации | 1988 |
|
SU1541648A1 |
| ИЗМЕРИТЕЛЬ ВРЕМЕННОЙ ЗАДЕРЖКИ СИГНАЛОВ В ДИНАМИЧЕСКИХ СИСТЕМАХ | 1992 |
|
RU2118847C1 |
| Генератор случайного процесса | 1983 |
|
SU1113801A1 |
| Субоптимальный фильтр для оценки параметра случайного процесса | 1989 |
|
SU1619307A1 |
| ГЕНЕРАТОР СЛУЧАЙНОГО ПРОЦЕССА | 1991 |
|
RU2050585C1 |
| Генератор случайного процесса | 1979 |
|
SU809127A1 |
| Устройство для определения законов распределения случайных процессов | 1982 |
|
SU1064284A2 |

ГЕНЕРАТОР СЛУЧАЙНЫХ ПРОЦЕССОВ, содержащий источник шума, первый усилитель, первый сумматор, первьй интегратор, первый линейный преобразователь, коммутатор, отличающийся тем, что, с целью расширения функциональных возможностей генератора путем обеспечения взаимной независимости одномерной плотности распределения слунайного процесса и его корреляционной функции, он содержит переключатель. три усилителя, три нелинейных преобразователя, второй сумматор, второй интегратор и второй линейный преобразователь, выход которого соединен с входами первого, второго и третьего нелинейных преобразователей, выходы которых соединены соответственно с первым, вторым и третьим входами коммутатора, вькод которого соединен с входом первого линейного преобразователя, выход которого является выходом генератора, выход источника шума соединен с входами первого и второго усилителей, выходы которых соединены соответственно с первыми входами пер- 5 вого и второго су 1маторов, выход (Л третьего усилителя соединен с вторым входом второго сумматора, выход первого сумматора соединен- с первым входом переключателя,выход которого через первый интегратор соединен с ; входами второго линейного преобразова, теля и четвертого усилителя, выход кото4; рого .соединен с третьим входом рого сумматора, выход которого через второй интегратор соединен с о ;о вторыми входами первого сумматора, и переключателя и с входом третьего усилителя.
(1Г)
(cos to Г + sinu)/f/) u
ie- созшТ
(1 + C/r/)
U)0,
P-. /5 0
r ±, w- 0
В
Область Sa - ро.спределен1
/
iO
фиг.2
Л. oSfiacmt,
Область -pacnpede/fenuu .
-Х It «
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Устройство для моделирования случайных процессов | 1973 |
|
SU452841A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Интегральные операционные усилители | |||
| М., Энер гоиздат, 1982, гл | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
Авторы
Даты
1985-02-23—Публикация
1983-10-18—Подача