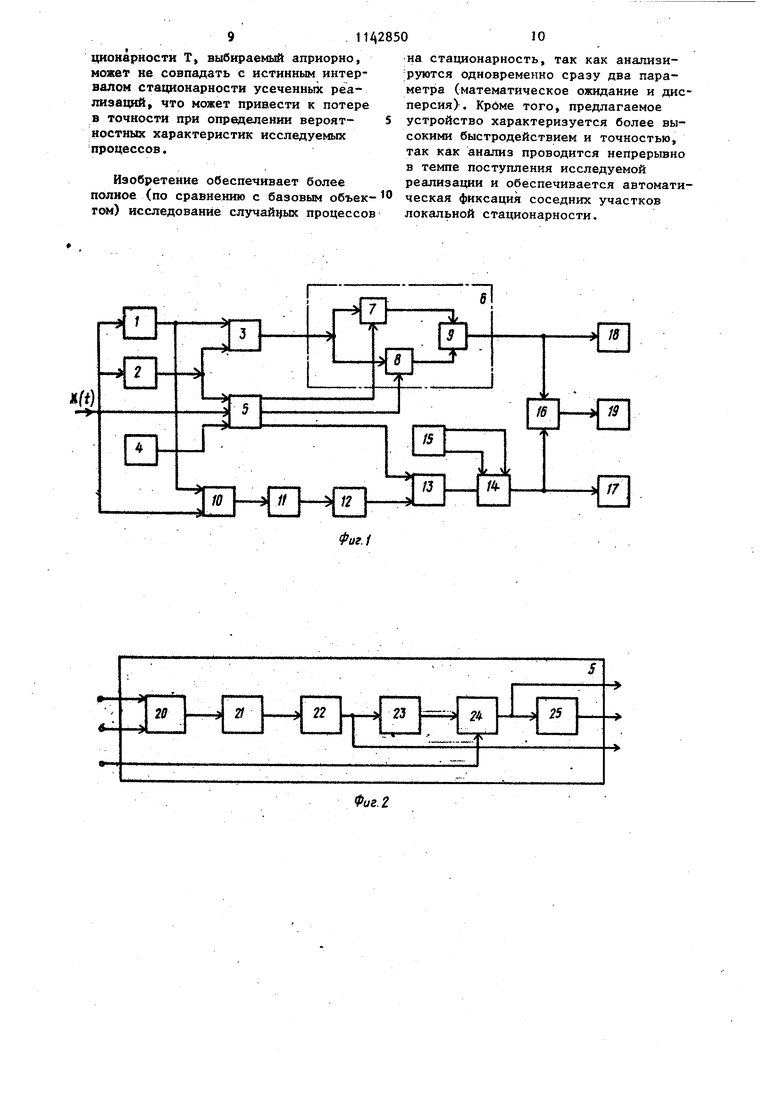
Изобретение относится к вычислительной технике и предназначено для определения стационарности случайных процессов. По основно авт. св. № 1067513 известно устройство для определения стационарности случайных процесс ов, которое позволяет определить наличие или отсутствие стационарности класса случайных процессов, стационарных относительно математического ожидания, причем получение данных о стационарности исследуемых случайных процессов происходит в процессе про ведения эксперимента с выделением границ усеченных реализаций X-pCt) локальной стационарности. I Известное устройство состоит из блока задания начальных условий, блока формирования границ интервала блока анализа гипотезы, состоящего из первого и второго компараторов и элемента ИЛИ, выход которого явля ется выходом устройства, а первый и второй входы подключены соответст венно к выходам первого и второго компараторов, первые входы которых объединены и подключены к выходу блока сравнения; первого и второго усреднителей, выход первого из кото рых соединен с первым входом блока сравнения, второй вход которого объ динен с первым информационным входом блока формирования границ интер вала и подключен к выходу второго блока усреднения, вход которого объ динен с входом первого усреднителя, с вторым информационным входом блок формирования границ интервала и является входом устройства, прямой и обратный выходы блока формировани границ интервала подключены соответ ственно к вторым входам первого и второго компараторов блока анализа гипотезы, а выход блока задания начальных условий подключен на третий информационньй вход блока форми рования границ интервала t1. Известное устройство позволяет определять наличие или отсутствие стационарности исследуемых случайны процессов относительно математического ожидания. В общем случае, при исследовании более широкого класса случайных процессов, для определени стационарности необходимо проверять инвариантность во времени математического ожидания и корреляционной функции исследуемого случайного процесса. Данное устройство оперирует лишь с математическим ожиданием, что является его недостатком. Цель изобретения - повышение точности при определении стационарности случайных процессов за счет введения в устройство еще одного контролируемого параметра - дисперсии исследуемого случайного процесса. В связи с тем, что дисперсия является нулевой ординатой корреляционной функции, то, вводя в рассмотрение дисперсию, можно получить характер изменения во времени корреляционной функции исследуемого процесса, так как маловероятно, чтобы нестационарный случайный процесс обладал корреляционной функцией, зависящей от времени t при всех значениях сдвига €, кроме Поставленная цель достигается тем, что в устройство для определения стационарности случайных процессов, содержащее первый блок задания начальных условий, блок формирования границ доверительного интервала, блок анализа гипотезы, первый и второй усреднители, блок сравнения, выход которого соединен с первым входом блока анализа гипотезы, первый вход блока сравнения подключен к вьгходу первого усреднителя, второй вход блока сравнения объединен с первым входом блока формирования доверительного интервала и подключен к выходу второго усреднителя, входы первого и второго усреднителей объединены со вторым входом блока формирования границ доверительного интервала и соединены со входом устройства, выход первого блока задания начальных условий подключен к третьему входу блока формирования границ доверительного интервала, первый и второй выходы которого соединены, соответственно, со вторым и третьим входами блока анализа гипотезы, введены блок центрирования, квадратор, третий усреднитель, умножитель, дополнительный блок анализа гипотезы, второй блок задания начальных условий, элемент И, первьй и второй входы которого соединены соответственно с выходами основного и дополнительного блоков анализа гипотезы и являются соответственно первым и вторым выходами устройства. 1142850 а выход элемента И является третьим выходом устройства, первый, второй и третий входы дополнительного блока анализа гипотезы подключены соответственно к первому и второму выходам j второго блока задания начальных условий и к выходу умножителя, первый вход которого соединен с выходом третьего усреднителя, вход которого подключен к входу,квадратора, вход 10 которого сбединен с выходом блока центрирования, первый вход которого подключен к выходу первого усреднителя, второй вход блока центрирования соединен с входом устройства, 15 второй вход умножителя подключен к третьему выходу блока формирования границ доверительного интервала. На фиг. 1 изображена блок-схема предлагаемого устройства; на фиг. 2 - jo выб блок-схема блока формирования грани интервала; на фиг. 3 - схема основн го и дополнительного блоков анализа гипотезы. Устройство содержит первый 1 и второй 2 усреднители, блок 3 срав нения, первый блок 4 задания началь ных условий, блок 5 формирования границ доверительного интервала, блок 6 анализа гипотезы, компараторы 7 и 8, злемент ИЛИ 9, блок 10 центрирования, квадратор 11, усреднитель 12, умножитель 13, дополнительный блок 14 анализа гипотезы, второй блок 15 задания начальных условий, злемент И 16, индикаторы 17 - 19, блок центрирования 20, квадратор 21, усреднитель 22, блок 23 вычисления корня, масштабирующий усилитель 24, инвертор 25. Основной 6 и дополнительный. 14 блоки анализа гипотезы вьшолнены по идентичной схеме (фиг. 3). При превьшении уровня напряжения на объеди ненных входах компараторов (А1 и А2 на фиг. 3) выше некоторой величины уставок напряжений на раздельных входах компараторов на выходе блока анализа гипотезы появляется сигнал. В основу функционирования предла гаемого устройства положены следующ известные вьфажения: .X-j. i -W 1-Р/4 где довкак но мый то и д соответственно генеральные среднее и дисперсия; X,S,S - соответственно выборочные среднее, среднеквадратичное отклонение и дисперсия по выборке объема и случайной величины X; квантили распределения Стьюдента, и Пирсона; число степеней свободы; объем выборки. Следовательно, определив границы ерительных интервалов (1,2) на ом-либо уровне значимости Р, можпредположить, что, если исследуеслучайный процесс стационарный, оценки математического ожидания X исперсии S, получаемые на основе орок той же реализации исследуеМОГО случайного процесса, для которой были составлены доверительные интервалы (1, 2), помещенные, соответственно, в вьфажения (1) и. (2), не выведут величины и S /d на границы соответствующих доверительных интервалов. Устройство работает следующим образом. Реализация исследуемого случайного процесса X(t) поступает на входы первого 1 и второго усреднителей 2 и на вторые входы блока 5 формирования границ доверительного интервала и блока 10 центрирования. С выхода усреднителей 1 и 2 снимаются величины напряжений, представляющие собой изменение во времени оценок математического ожидания случайного процесса X(t) . Период усреднения первого усреднителя 1 выставляется с учетом ползд1ения оценки математического ожидания, близкой по точности к истинному значению математического ожидания у случайного процесса X(t). Период усреднения второго усреднителя 2 выбирается с учетом того, чтобы точность получаемой оценки математического ожидания X аналоговым методом, соответствовала точности, с которой может быть получена аналогичная оценка на основании выборочных методов по выборке из п измерений случайного процесса. Блок 3 сравнения формирует сигнал, соответствующий разности указанных величин X-jn, который поступает на объединенные входы первого 7 и второго 8 компараторов основного блока 6 анализа гипотезы; где сравнивается с сигналами, соответствующими верхней и нижней границам доверительного интервала (1), поступающими с прямого и обратного выходов блока 5 формирования границ доверительного интервала . Границы доверительного интервала формируются следующим образом. На первый и второй входы блока центрирования 20 блока 5 формирования границ доверительного интервала поступают сигнал, пропорциональный оценке математического ожидания X с выхода усреднителя 2 усреднения, и исследуемый случайный процесс X(t) соответственно. В результате последовательного преобразования указанных сигналов блоком центрирования 20 кваДратором 21, усреднителем 22 на выходе последнего происходит измене ние во времени оценки дисперсии S. Указанная величина поступает на вход блока 23 вычисления корня блока 5 формирования границ интервала, на выходе блока 23 происходит изменени во времени оценки среднеквадратичного отклонения S. Умножение величины S на величину t. осуществляется изменением отрицательной обратной связи масштабирующего усилителя 24 блока 5 формирования границ доверительного интервала, а имен но - подключением в обратную связь усилителя соответствующего сопротивления из магазина сопротивлений первого блока 4 задания начальных условий. Номинал подключаемого сопротивления эквивалентен умножению величины S.на требуемую в ходе данного эксперимента величину t,,-р/ /l/iT. В результате на прямом и обратном вьйсодах блока 5 формирования границ доверительного интервала устанавливается соответственно верхняя +St.pr/Vn и нижняя -St.p /Vrf границы доверительного интервала (1). 1 Следовательно, выдвинув гипотезу о стационарности исследуемого случайного процесса на некотором уровне значимости, для чего производится подключение соответствующего сопротивления из магазина сопротивлений первого блока 4 задания начальных условий на третий вход блока 5 формирования границ доверительного интервала, можно утверждать, что если исследуемый случайный процесс стационарный, то величина находится в границах доверительного интервала (1.) и, следовательно, сигнал на выходе первого блока 6 анализа гипотезы отсутствует, В противном случае, при появлении сигнала (что фиксирует первый индикатор 18), гипотезу о стационарности исследуемого случайного процесса относительно среднего следует отклонить на заданном уровне значимости. Кроме того, на первый и второй входы блока 10 центрирования соответственно поступают сигнал, пропорциональный оценке математического ожидания с выхода первого усреднителя 1, и исследуемый случайный процесс. В результате последователького преобразования указанных сигналов блоком 10 центрирования,квадратором 11 и третьим усреднителем 12 на выходе последнего происходит изменение во времени оценки дисперсии t . Период усреднения блока 12 выставляется с учетом получения оценки дисперсии, близкой по точности к истинному значению дисперсии d случайного процесса X(t). Сигнал, соответствующий искомой оценке, поступает на второй вход умнозкителя 13, на первый вход которого с выхода усреднителя 22 блока 5 формирования границ доверительного интервала поступает сигнал, пропорциональный оценке дисперсии S, полученньй по меньшему периоду усреднения. С выхода умножителя 13 сигнал, пропорциональный частному от деления входных сигналов, поступает на первый вход дополнительного блока 14 анализа гипотезы, где сравнивается с величиной верхней и нижней границ доверительного интервала (2), поступающих в виде опорных напряжений на второй и третий входы дополнительного блока 14 анализа гипотезы с соответствующих выходов второго блока 15 задания начальных условий. Следовательно, вьщвинув гипотезу о стационарностиИсследуемого случайного процесса на некотором уровне значимости Р для чего производится подключение соответствующих источников опорного напряжения во втором блоке 15 задания начальных условий на второй и третий входы дополнительного блока 14 анализа, можно утверждать, что если исследуемый случайный процесс стационарный, то величи на 2 находится в границах доверительного интервала (2) и, следовательно, сигнал на выходе дополнительного блока 14 анализа гипотезы отсутствует. Это означает, что корреляционная функция исследуемого случайного процесса инвариантна во времени. Так, как уже отмечалось, по инвариантности дисперсии, которая является нулевой ординатой корреляционной функции, можно СУЩ1ТЪ об инвариантности всей функции, так как мало вероятно, чтобы нестационарный случайный процесс обладал корреляционной функцией, зависящей от времени при всех значениях сдвига Г, кроме . В противном случае, при появлеНИИ сигнала на выходе блока 14 (что фиксирует третий индикатор 17), гипо тезу о стационарности (инвариантности корреляционной функции во времени) исследуемого случайного процесса следует отклонить на заданном уровне значимости Р. С выходов основного 6 и дополнительного 14 блоков анализа гипотезы сигналы поступают на соответствующие входы элемента И 16. При совпадении сигналов на его входах на выходе элемента И 16 появляется сигнал (что фиксирует второй индикатор 19), который информир ует исследователя об отсутствии стационарности как по математическому ожиданию, так и по кррреляционной функции, на уровне значимости Р. В общем случае, при исследовании квазистационарных случайных процессов, о характеристиках которых судя по усеченньм реализациям X(t),. где Т - длительность усеченного участка локальной стационарности, сигналы индикаторов фиксируют границу соседних участков. Указанное разделение участков локальной стационарности важно иметь при экспрессобработке поступающей информации с использованием алгоритмов получени оценок для стационарных эргодических случайных процессов, так как незнание длительности отдельных участков может привести либо к потере в точности определения оценок, если огра ничиться малым периодом усреднения, либо при увеличении длительности периода Т к искажению -оценок вероятностных характеристик за счет попада ния в интервал усреднения значений соседних граничных участков усеченных реализаций X.(t) локальной стационарности. Предлагаемое устройство работоспособно через период времени, равный периоду усреднения первого 1 и третьего 12 усреднителей, после его включения в цепь измерения. Предлагаемое устройство в отличие от прототипа позволяет получать экспресс-анализ о стационарности исследуемого случайного процесса с более высокой точностью за счет введения еще одного контролируемого параметра - дисперсии случайного процесса. Кроме того, расширяется класс случайных процессов, обрабатываемых данным устройством. В прототипе могли исследоваться лишь процессы со стационарностью относительно математического ожидания. Применение изобретения в процессе проведения экспериментов позволяет повысить эффективность исследования случайных процессов. В связи с тем, что промьшшенностью не выпускаются устройства подобного типа, за базовый объект может быть взята вычислительная машина, на которой можно программным путем организовать проверку выполнения условий на стационарность исследуемого случайного процесса, например, по известноъгу алгоритму, базирующемуся на непараметрическом критерии серий, который обеспечивает проверку наличия или отсутствия стационарности случайных процессов относительно их вероятностных характеристик (математического ожидания, дисперсии, среднего значения квадрата). К недостаткам указанного метода следует отнести невозможность организации анализа в экспресс-режиме (так как необходимо занести всю выборку исследуемого случайного процесса в память ЦВМ) . Кроме того, алгоритм, основанный на критерии серий, позволяет определять стационарность случайного процесса на некотором фиксированном интервале длительности Т. В общем случае, когда исследуются квазистационарные процессы, о характеристиках которых судят по усеченным реализациям X(t), интервал определения стационарности Т, выбираемый априорно, может не совпадать с истинным интервалом стационарности усеченных реализахщй, что может привести к потере в точности при определении вероятностных характеристик исследуемых процессов. Изобретение обеспечивает более полное (по сравнению с базовым объектом) исследование случайных процессов на стационарность, так как анализируются одновременно сразу два параметра (математическое ожидание и дисперсия) . Крбме того, предлагаемое устройство характеризуется более высокими быстродействием и точностью, так как анализ проводится непрерывно в темпе поступления исследуемой реализации и обеспечивается автоматическая фиксация соседних участков локальной стационарности.



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для определения стационарности случайных процессов | 1981 |
|
SU1067513A1 |
| Адаптивное устройство для определения среднего значения случайного процесса | 1982 |
|
SU1043664A1 |
| Устройство для измерения корреляционного отношения двух случайных процессов | 1977 |
|
SU696488A2 |
| Устройство для измерения корреляционногоОТНОшЕНия дВуХ СлучАйНыХ пРОцЕССОВ | 1979 |
|
SU851420A2 |
| Статистический анализатор | 1981 |
|
SU1003096A1 |
| Анализатор момента изменения характеристик случайных низкочастотных процессов | 1986 |
|
SU1322330A1 |
| ЦИФРОВОЙ ОПРЕДЕЛИТЕЛЬ ДИСПЕРСИИ | 1972 |
|
SU424159A1 |
| Устройство для определения вероятностных характеристик фазы случайного процесса | 1985 |
|
SU1300510A2 |
| Устройство для определения стационарности случайного процесса | 1981 |
|
SU1035612A1 |
| Устройство для испытаний на случайные вибрации | 1989 |
|
SU1704005A1 |

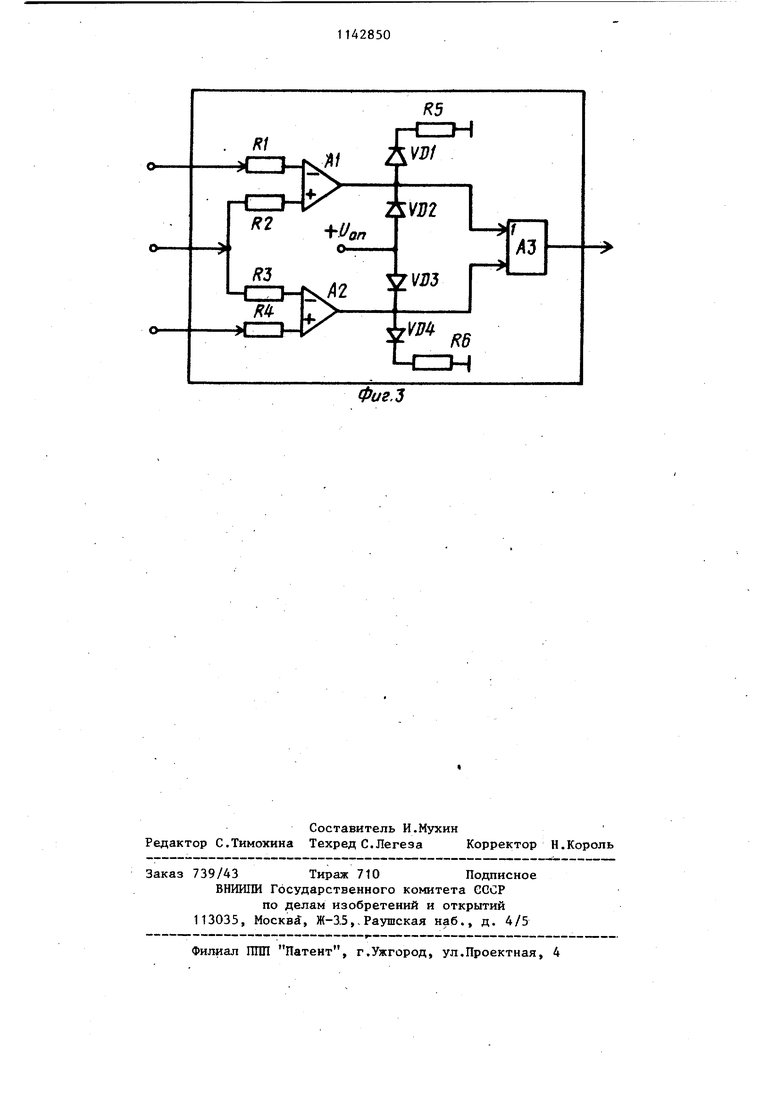
УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ СТАВДОНАРНОСТИ СЛУЧАЙНЫХ ПРОЦЕССОВ по авт. ей, № 1067513, отличающее с я тем, что, с целью повышения точности, в него введеныблок центрирования, квадратор, третий усреднитель, умножитель, дополнительный блок анализа Гипотезы, второй блок задания начальных условий, эле: мент И, первый и второй входы которого соединены соответственно с выходами основного и дополнительного блоков анализа гипотезы и являются соответственно первым и вторым выходами устройства, а выход элемента И является третьим выходом устройства, первый, второй и третий входы дополнительного блока анализа гипотезы подключены соответственно к первому и второму выходам второго блока задания начальных условий и к выходу умножителя, первый вход которого соединен с выходом третьего усреднителя, вход которого подключен к выходу квадратора, вход которого соединен с выходом блока центрирования, первый вход которого подключен к вы(Л ходу, первого усредцителя, второй вход блока центрирования соединен с с входом устройства, второй вход умножителя подключен к третьему выходу блока формирования границ доверительного интервала.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Устройство для определения стационарности случайных процессов | 1981 |
|
SU1067513A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1985-02-28—Публикация
1983-07-20—Подача