Изобретение относится к автоматике и вычислительной техвшке, в частности к программному управлению технологическим оборудованием, и может быть использовано в про- граммируемых системах управления технологическими объектами, алгоритм управления которых описывается с помощью булевых функций, в частности в программируемых контроллерах и управляющих вычислительных машинах.
Устройство для вычисления булевых функций позволяет вычислять скобочные формы булевых функций, представленных в виде лестничной диаграммы. Наряду с такой формой представления булевых функций в техн1псе используется представление булевых функций в спде компактной записи и- в форме алгебраических уравнений. При этом существует необходимость создания устройства, реализующего любую сколь угодно сложную булевую функцию, Лредст авленную в форме алгебраического уравнения.
Цель изобретения - расширение области применения за счет реализации любых скобочных форм булевых функций, представленных в виде алгебраических уравнений.
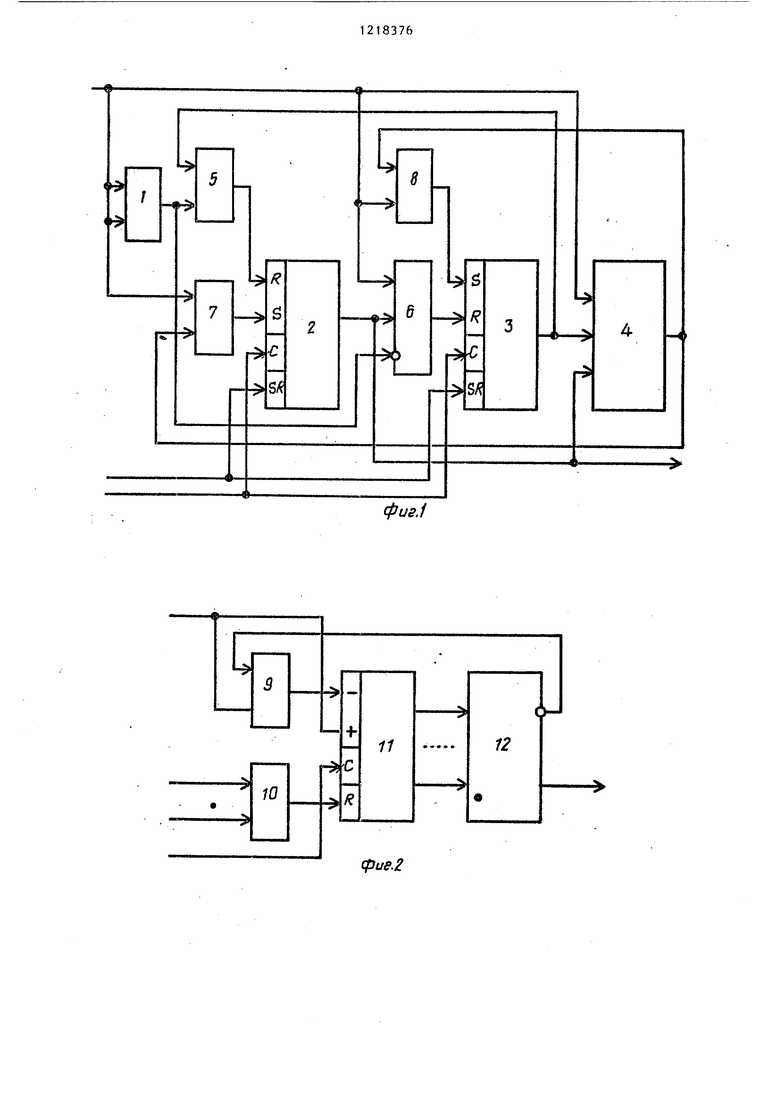
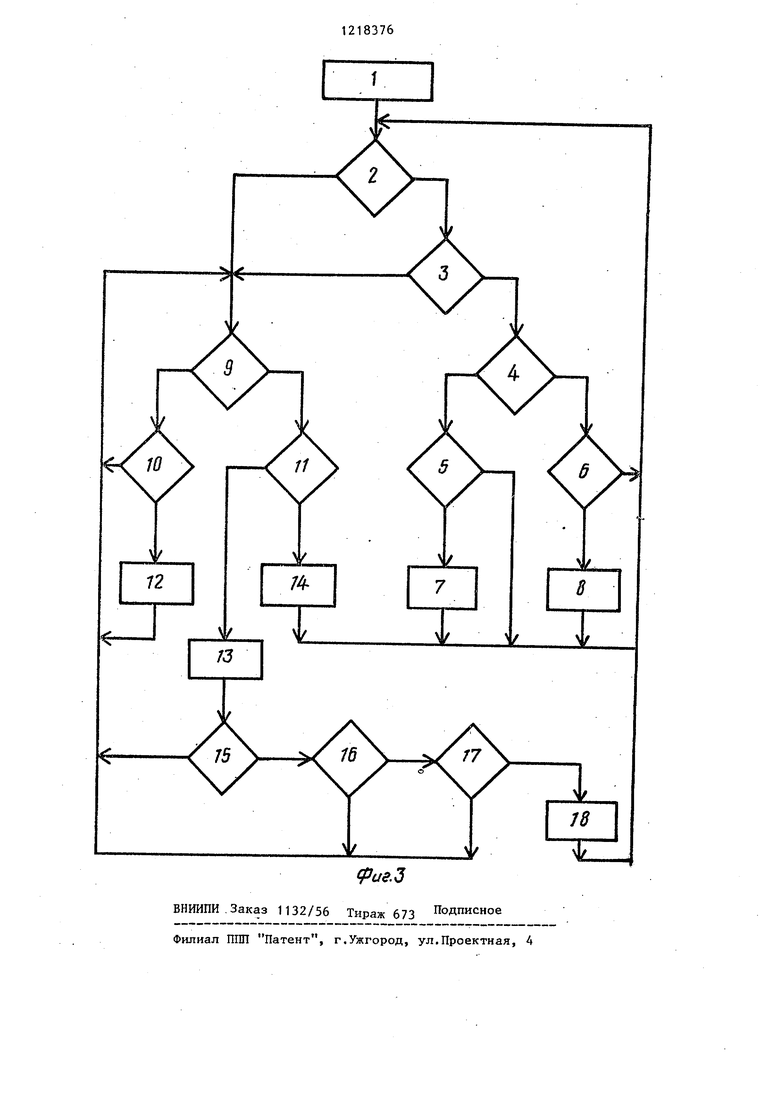
Па фиг. 1 представлена схема устройства; на фиг. 2 - схема узла счет на фиг, 3 - блок-схема алгоритма работы устройства.
Устройство содержит элемент ИС1Ш10ЧЛЮЩЕЕ 1ПИ 1, триггеры 2 и 3, узел 4 счета, элементы И 5-8.
Узел счета содержит элементы И 9-10, реверсивный счетчик 11 и дешифратор 12.
Блоки блок-схемы алгоритма работы устройства выполняют следующие действия: блок 1 - установить состояние триггеров 2 и 3 равное единице5 блок 2 - проверить состояние триггера 2 на равенство едтище , блок 3 - проверить состояние трихтера 3 на равенство единице; блок 4 - проверит совпадает ли действительное значение аргумента со значением аргумента, указанным в управлении; блоки 5 и 6- проверить наличие знака дизъюнкции , блок 7 - установить состояние триггера 3 равное нулю , блок 8 - установить состояние триггера 2 равное нулю; блок 9 - проверить наличие знака Закрывающая скобка ); блок 10 - проверить наличие знака Открывающая скобка (j блок 11
5
j 0 5
55
5
0
5
проверить состояние счетчика 11 на равенство нулю; блок 12 - инкременти- ровать содержимое счетчика 11; блок 13 - декрементировать содержимое счетчика 11; блок 14 - установить триггер 3 в единичное состояние; блок 15 - проверить.состояние ра 2 на равенство нулю; блок 16 - проверить состояние счетчика 11 на равенство нулю , блок 17 - проверить наличие знака дизъюнкции блок 18 - установить триггер 2 в единичное состояние.
Устройство использует для вычисления булевых функций алгебраических
уравнений знак дизъюнкции +, открывающие и закрывающие скобки, что дает возможность реализовать скобочные формы булевых функций, представленные в виде алгебраических уравнений. При этом отпадает необходимость в разработке принципиальных электрических схем за счет того, что программирование производится непосредственно по уравнению, а не по электрической схеме. Максимально облегчается труд программиста, так как любое уравнение является и программой его решения, поэтому для программирования достаточно просто переписать это уравнение в память устройства без каких-либо преобразований. Кроме того, программирование по уравнению:, -позволяет автоматизировать ввод программы (например вводить программу от вычислительной машины).
Решрггь булевое уравнение - значит найти его значение па данном наборе аргументов. Для любого буле- вого уравнения вычисления ведут,в порядке естественной записи аргументов, т.е. слева направо.
Пример уравпения:
XI (Х2 + ХЗ + Х4) X (Х5 + КХ7 + Х8)) X Х9 + Х10 Y (1)
Индексы при аргументах определяют порядок вычисления.
В начале вычисления устанавливают значение функции, равное 1. Решают уравнение, вычисляя последовательно аргументы в следующем порядке. Обо- значают единицей значение аргумента, указанное в уравнении, если этот аргумент записан для знака инверсии (аргументы XI, X 3, Х4, Х5, Х7, Х8, Х9, Х10 в уравнении (1), и соответственно обозначают нулем,
если этот аргумент записан со знаком инверсии (аргументы Х2 и Х6 в уравнении (1). При таком обозначении совпадение действительного значения аргумента и значения аргумента, указанного в уравнении, означает, что аргумент истинен (т.е. его вычисленное значение равно единице), несовпадение этих значений означает, что аргумент ложен (т.е. его вычисленное значение равно нулю). Составляют табл. 1 по результатам
этих вычислений
Таблица 1
Как видно из данных табл, 1, для вычисления аргумента можно использовать элемент провеки на четность (ИСКЛЮЧАЮЩЕЕ ИЛИ с инверсией) .
Если на входы элемента подавать сигналы действительного значения аргумента и значения, указанного в уравнении, то на выходе получают вычисленное значение аргумента.
В процессе вычисления уравнения существует два условных перехода: когда вычисленный аргумент истинен и после него стоит знак дизъюнкции + когда вычисленный аргумент ложен и после него нет знака дизъюнкции (т.е. стоит знак конъюнкции) .
В примере - уравнение (1) - зцак .дизъюнкции стоит после аргументов Х2, ХЗ, ., Х7, Х9.
В первом :лучае процедура условного перехода такова: функции присваивается значение 1, накладывается запрет на вычисление остальных слагаемых дизъюнкций до отыскания последнего аргументау входящего в
0
данную дизъюнкцию, после чего вычисление продолжается.
Если уравнение заканчивается последним членом этой дизъюнкции, то результатом решения данного уравнения будет единица.
Во втором случае функции присваивается значение ноль, накладывается запрет на вычисление остальных
O сомножителей данной конъюнкции
до отыскания последнего аргумента, обнаруживается дизъюнктивный член iK той части функции, в которую входит только что вычисленная
5 Iконъюнкция, функции присваивается значение 1 и вычисление продолжается. Если уравнение заканчивается последним членом данной конъюнкции, то результатом решения этого уравнения будет 0.
Эти правила вытекают из предложений булевой алгебры: если в дизъюнкции хотя бы один из слагаемых равен единице, то вся дизъюнкция
5 равна единице, если в конъюнкции хотя бы один из сомножителей равен нулю, то вся конъюнкция обращается в нуль.
Устанавливают правило для отысд кания последнего аргумента дизъюнкции при первом условном переходе. Для этого рассматривают дизъюнкцию
Х1+Х2+ХЗ... +Хп Y (2).
Если эта дизъюнкция входит в состав более сложного аргумента,
то она должна быть заключена в
скобки /Х1+Х2+ХЗ+... +Хп/ (3) или Хп+1 /ХИ-Х2+ХЗ+... (4) где Хп+1 и Хп+2 - любые, сколь угод- но сложные аргументы.
Из уравнений (3) и (4) видно, что окончание дизъюнкции определяется наличием закрывающей скобки. Однако любой член дизъюнкции может быть сложным аргументом, в свою
очередь содержащим скобки. .Например, Х2 АЗ,//, + Л,/, тогда уравнение (3) примет вид /Х1+ АЭ/Д, + А /+ХЗ+...+ +ХП/ХП+1 Y (5).
При этом по ходу вычисления, ес0 ли например имеется закрывающая скобка после аргумента Aj.- которая не характеризует окончание данной дизъюнкции. Такие скобки, принадлежащие сложным аргументам,.
5 характеризуются тем, что каждой закрывающей скобке соответствует открывающая скобка и лишь последняя закрывающая скобка, указывающая
на конец дизъюнкции, оказывается нескомпенсированной открывающей скобкой. Поэтому правило для отыскания последнего члена дизъюнкции можно трактовать так; по ходу вычисления подсчитывается количество открывающих и закрывающих скобок и тот наиболее близкий шаг вычислений, в котором число закрывающих скобок хотя бы на одну больше числа открывающих скобок, указывает на конец дизъюнкции.
Устанавливают правило для отыскания последнего аргумента конъюнкции нри втором условном переходе. Для этого рассматривают конъюнкцию
xb-xz- xa. .. .хп Y (6)..
1 ;сли эта конъюнкция входит в состав более сложного аргумента, то после нее должен стоять знак дизъюнкции, с помощью которого к ней присоединяется в общем случае любой, сколь угодно сложный аргу- .
мент
Х1 Х2 ХЗ ...Xn+Xn-f-1 (7)
Из уравнения (7) видно, что окончание конъюнкции определяется наличием знака дизъюнкции +. Однако каждый из аргументов Х+Хп может быть сколь угодно сложным, содержащим в свою очередь знаки дизъюнкцliи. Например, Х2 Лт + Л.; . Такие аргументы заключаются в скобк ХЬ/А, + А,...Хп + Xn-i-1 Y (8)
Тогда перед каждым знаком дизъЕонкции, входящим в сомножитель вычисляемой конъюнкции, должна быть открывающая скобка и лишь в том случае, когда все открывающие скобки скомпенсированы закрывающими скобками, знак дизъюнкции + является указанием на окончание конъюнкции. Тогда правило для отыскания последнего члена конъюнкции можно трактовать так: по ходу вычисления подсчитывается количество открывающих и закрывающих скобок, причем закрывающие скобки считаются лишь тогда, если имеется хотя бы одна открывающая скобка. Если разность между числом открывающих и закрывающих скобок равна нулю, то наиболее близкий по ходу вычисления знак дизъюнкции + указывает на окончание конъюнкции.
Элемент ИСКГПОЧАЮЩЕЕ ИЛИ 1 (фиг. 1) устройства служит для вы0
5
0
5
0
0
5
0
5
числения аргумента. Триггер 2 служит для хранения текущего и вычисленного значения функции. Выход триггера 2 является выходом устройства. Сигнал, снимаемый с этого вы- хода, есть вычисленное значё ние функции. Установка триггера 2 в нулевое состояние определяет начало второго условного перехода. Триггер 3 служит для фиксации первого условного перехода, установка триггера 3 в нулевое состояние определяет начало первого условного перехода.
Узел 4 счета служит для подсчета открывающих и закрывающих скобок уравнения в процессе условных переходов. Узел 4 счета (фиг. 2) может, например, состоять из двоичного реверсивного счетчика 11 и деш1фра- тора 12. Двоичньй реверсивный счетчик имеет входы Сложение и Вычитание, а также входы установки нуля и синхронизации. Если.выходы триггеров 2 и 3 через элемент И 10 соединить с входом установки нуля счетчика, то перевод любого из триггеров в нулевое состояние будет сигналом для начала подсчета открывающих и закрывающих скобок. При этом, если на вход Сложение подавать сигналы Открывающая скобка ), а на вход Вычитание - подавать сигналы Закрывающая скобка ( и начинать подсчет закрывающих скобок, если счетчик не находится в нуле, т.е. когда была подсчитана хотя бы одна открывающая скобка, то нулевое состояние счетчика всегда определяет, что по ходу вычисления , все открывающие скобки скомпенсированы закрывающими. При этом можно использовать дешифратор числа 0.
Единичньш сигнал на выходе этого дешифратора и наличие по ходу вычисления закрывающей скобки определяют окончание первого условного перехода. В этом случае на обоих входах элемента И 8 будут единичные сигналы и триггер 3 переведется в единичное состояние. Единичный сигнал на выходе дешифратора и наличие по ходу вычисления знака Дизъюнкция определяют окончание второго условного перехода, при этом на обоих входах элемента И 7 будут единичные сигналы и триггер 2 переведется в единичное состояние.
Входы установки единицы триггер 2 и 3 имеют приоритет над входами установки нуля.
Устройство работает следующим образом.
Перед каждымциклом вычисления подается сигнал Установка устройства в исходное состояние. Тригге ры 2 и 3 устанавливаются в единичное состояние. В процессе вычисления через управляющий вход устройства на вход элемента ИСКЛЮЧАЮЩЕЕ ИЛИ 1 подается сигнал Значение аргумента, указанное в уравнении, на входы элементов И 6, 7 подается сигнал Дизъюнкция, на вход элемента И 8 подается сигнал Закрывающая скобка J и на вход узла 4 счета подаются сигналы Открывающая скобка ( и Закрывающая скобка ). Эти сигналы подаются в том порядке, как они записаны в уравне- ,нии.
Когда на всех входах устройства установятся сигналы, подается сигна синхронизации, по переднему фронту которого переключаются триггеры 2 и 3 и узел 4 счета. При подаче на один вход элемента ИСКЛЮЧАЮЩЕЕ ИЛИ сигнала Значение аргумента, указанное в уравнении на другой вход элемента ИСКЛЮЧА10ЩЕЕ 1ШИ 1 подается действительное значение аргумента. Если эти значения совпадают, т.-е. на обоих входах будет либо нуль, либо единица, то на выходе элемента будет нуль, и если есть знак Дизъюнкция, то триггер 3 переводится в нулевое состояние, так как на входах элемента И 6 будут единичные сигналы. При этом накладывается запрет на вычисление последующих аргументов, так как на входе элемента И 5, соединенном с выходом триггера 3, будет нулевой сигнал. Одновременно узел 4 счета подготавливается к отсчету открывающих и закрывающих скобок. Если по ходу вычисления все открывающие
«
скобки будут скомпенсированы закрывающими скобками и имеется лишняя закрывающая скобка (частный случай, 5 когда между знаком дизъюнкции и закрывающей скобкой нет ни одной открывающей скобки), то на обоих входах элемента И 8 будут единицы и триггер 3 через вход установки
0 единицы будет переведен в единичное, .состояние.
Если действительное значение аргумента и значение аргумента, указанное в уравнении, не совпадают, то
5 на выходе элемента ИСКЛЮЧАЮЩЕЕ ИЛИ 1 будет единица, и если нет знака Дизъюнкция, то по входу установки нуля триггер 2 переведется в нулевое состояние. При этом узел 4 сче0 та будет подготовлен к отсчету открывающих и закрывающих скобок. Если по ходу вычисления все открывающие скобки будут скомпенсированы закрывающими и имеется знак Дизъюнкция
5 (частный случай, когда после вычисленного аргумента сразу же стоит знак дизъюнкции), то на обоих входах элемента И 7 будут- единицы, триггер 2 будет переведен в единич0 ное состояние, и вычисление продолжается.
После вычисления последнего аргумента уравнения значение функции (О или 1) снимается с выхода триг, гера 2. Это значение является результатом решения уравнения.
Рассмотрим пример вычисления конкретной булевой функции, записанной в виде алгебраического уравнения 0 Х-1+Х2/ХЗ«/Х4+Х5/+Х6д Х7/+Х8/Х94.
+Х10/Х1И-Х12/Х13+Х14/+Х15 Y. Предположим, действительное зна- « чение аргументов ХЗ, Х7, Х8, Х9, XI3 совпадает со значением аргу- ментов, записанным в уравнений,
а действительное значение остальных аргументов - не совпадает.
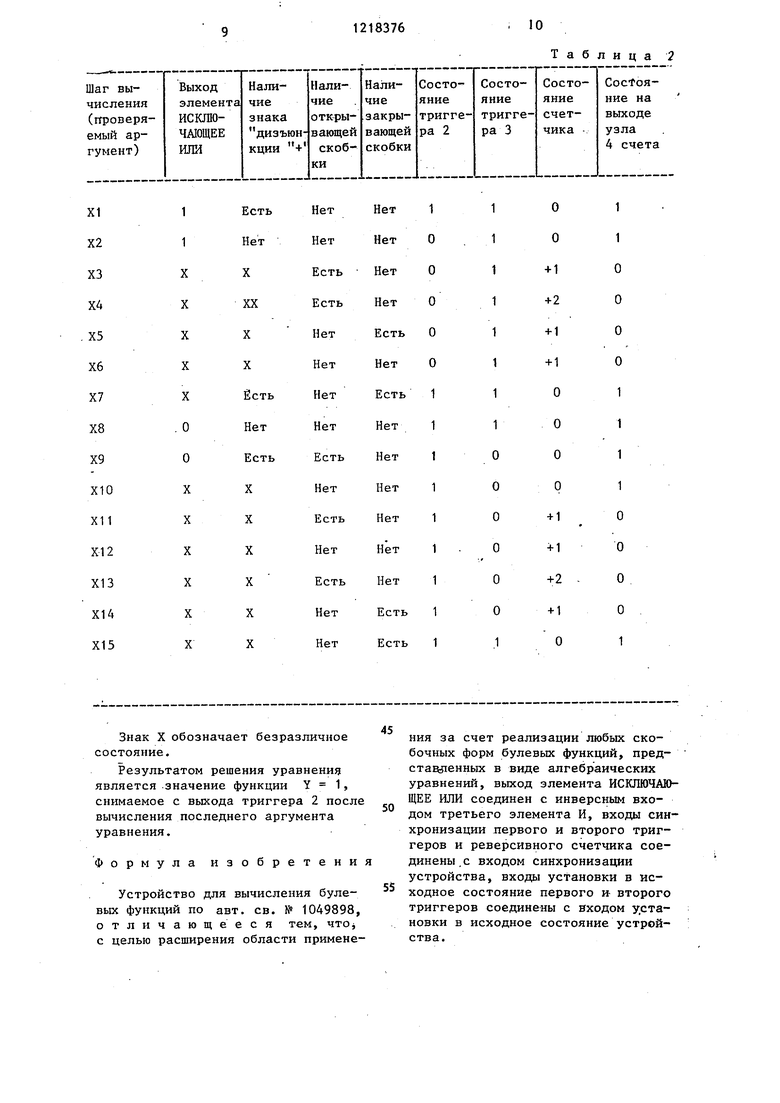
Результаты решения уравнения сведем в табл. 2.
Знак X обозначает безразличное состояние.
Результатом решения уравнения является значение функции Y 1, снимаемое с выхода триггера 2 после вычисления последнего аргумента уравнения.
Формула изобретени
Устройство для вычисления буле- вьк функций по авт. св. № 1049898, отличающееся тем, 4TOj с целью расширения области применеТаблица 2
ния за счет реализации любых скобочных форм булевых функций, представленных в виде алгебраических уравнений, выход элемента ИСКЛЮЧАЮЩЕЕ ИЛИ соединен с инверсным входом третьего элемента И, входы синхронизации первого и второго триггеров и реверсивного счетчика соединены, с входом синхронизации устройства, входы установки в исходное состояние первого и второго триггеров соединены с входом установки в исходное состояние устройства.
фие.1
ВНИИПИ. Заказ 1132/56 Тираж 673 Подписное Филиал ППП Патент, г.Ужгород, ул.Проектная, 4
fpae.S



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления булевых функций | 1982 |
|
SU1049898A1 |
| Устройство для вычисления булевых функций | 1984 |
|
SU1242928A1 |
| Устройство для вычисления булевых функций | 1986 |
|
SU1372319A1 |
| Устройство для вычисления булевыхфуНКций | 1978 |
|
SU807272A1 |
| Устройство для вычисления булевых функций | 1984 |
|
SU1254462A1 |
| Устройство для вычисления булевых функций | 1980 |
|
SU955027A1 |
| Устройство для вычисления систем булевых функций | 1989 |
|
SU1644126A1 |
| Устройство для подсчета числа ответвлений диаграммы | 1983 |
|
SU1160391A1 |
| Устройство для моделирования конечных автоматов | 1980 |
|
SU955080A1 |
| Устройство для определения значений булевых функций | 1984 |
|
SU1262475A1 |
Изобретение относится к автоматике и вычислительной технике и может быть использовано в программируемых системах управления технологическими объектами, алгоритм управления которых описывается с помощью булевых функций, в частности в программируемых контроллерах и управляющих вычислительных машинах. Цель изобретения - расширение об-, ласти применения устройства за счет реализации любых скобочных форм бу- левьпс функций, представленных в виде алгебраических уравнений. Устройство содержит элементы И, элемент ИСКЛЮЧАВДЕЕ ИЛИ, первый и второй триггеры, узел счета скобок. В процессе вычисления на информационный вход подаются действительные значения аргументов, на управляющие входы - сигналы Значение аргумента, указанное в уравнении, Дизъюнкция, Закрывающая скобка, Открывающая скобка. Эти сигналы подаются в том порядке, в котором соответствующие им символы записаны в уравнении. После вычисления последнего аргумента уравнения значение функции снимается с выхода первого триггера. Изобретение дополнительное к авт.св. № 1049898. 3 ил, 2 табл. (Л с § 1C СХ) со а

| Устройство для вычисления булевых функций | 1982 |
|
SU1049898A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1986-03-15—Публикация
1984-09-04—Подача