чивающий подвижное соединение поворотных планок 5 и 8, а также круговое движение прозрачного сектора 10 с оцифрованными дугами 11. Для снятия отсчета со шкалы лимба в планке выполнено окошко 12. На линейке 1 нанесены две шкалы: основная 13 с прямым направлением отсчета от нуля до десяти, обеспечивающая увеличение какой- либо из координат точки (X или Z) в К раз, и дополнительная 14 с обратным направлением отсчета от единицы до нуля, обеспечивающая уменьшение любой из координат точки в 1/К раз К .
В основу решения обобщенной задачи коммивояжера положено эвристическое правило идти в ближайшую точку. Обобщение задачи коммивояжера заклю- чается в неравноценности затрат по продольной X и боковой Z осям при переходе из одной точки в другую. В прототипе показано, что полные затраты при переходе из точки N; в точку N. равны:
ai.l-fjj A tfbrfV (,)
aix,ai74 .
где ---(---) - функции влияния, харако л дь
теризующие приращение затрат при переходе из одной точки в другую, находящуюся на единичном расстоянии в X(Z)- направлении;
ЛХ; (ZSZ ;:) - приращение координат точки N, в Х(2)-на- правлении относительно координат точки N.. Уравнение (1) можно записать в ви
1 -Ai, . /52Zij
1 Т +
а &
(2)
/51, L/31ч
где а л;7Й ъ
Преобразуем уравнение (2) к виду
а-лх (J azsj)4,
(3)
Обозначим коэффициент перед AZ.. через К, т.е.
а 31а , 8Ь
ь sz ах
К & Zij,
что эквивалентно введению новой системы координат, в которой проекция точки маршрута будет отличаться от проекции I в системе координат XZ в К pai.
С учетом (4) и (5) уравнение (3) примет вид
аг 4х,: + д г,
(6)
м - - J
Аналогичные преобразования с координатой X приводят к выражению
Ь УХ + дг,
клхм
(7) (8)
0 5
0
Q
5
5
0
5
Выражения (6) и (7) являются уравнениями окружностей радиусом а и b соответственно. Совокупность графиков этих окружностей представляет собой изолинии уровня затрат при переходе из центра на любую точку окружности.
Переход от действительных координат точек маршрута к псевдокоординатам по формулам (5) или (8) возможен четырьмя способами:
1)при К 1 координаты по Z увеличиваются в К раз;
2)при К I координаты по X увеличиваются в К раз;
3)при К 1 координаты по Z уменьшаются в К раз;
4)при ,К 1 координаты по X уменьшаются в К раз.
При выборе способа предпочтение следует отдавать первым двум,поскольку увеличение координат не скажется на потере точности решения задачи. При этом необходимо также учитывать соответствующую соизмеримость масштаба карты (графика) с размерами устройства.
Таким образом, если перейти от действительных координат точек маршрута , Z ij к псевдокоординатам 4X,j, dZ .j по формуле (5) или к псевдокоординатам по формуле (8), то пространство в новых переменных будет изотропным в смысле равноценности затрат для любых направлений движения. Исходя из вышеприведенных соотношений, эти затраты определяются следующим образом:
- ai
Л1
, + 4It .- М г 1)
+AZ }.
эх
Э1х
Jx va
(9)
В свою очередь, радиус дуги окружности может быть представлен выражением
а 10 N , (10) где t0 - радиус первой (единичной) дуги окружности или равное ему приращение радиусов последующих дуг окружностей; N - ближайший к рассматриваемой точке порядковый -номер дуги окружности (для большей точности определения затрат на переход от точки к точке N не обязательно должно быть целым числом).
С учетом (10) выражение (9) примет вид:
51х ,.
Jx г 3
N
01)
В выражении (11) произведение
I
5х г° Сх
02)
представляет собой нормированную для конкретной задачи цену деления.
Таким образом, затраты при переходе от точки i к точке j будут вычисляться по формуле
N
(13)
При введении псевдокоординат по оси затраты будут определяться аналогичным выражением
41,-i
N
(14)
где
ill. r 3Z °
Для оценки затрат на переход из точки i в точку j необходимо снять отсчет с дуги окружности прозрачного сектора, которой накрывается данная псевдоточка маршрута, и умножить это число на цену деления сх при введении псевдокоординат по оси X или на cz при введении псевдокоординат по оси Z.
Линейку и поворотные планки рекомендуется изготовлять из жесткого легкого материала. Сектор должен быть изготовлен из прозрачного материала на который наносятся оцифрованные концентрические дуги с равными приращениями радиуса. Частота нанесения дуг и масштаб, а следовательно, и размеры сектора в отличие от планщета у прототипа могут быть од5
нотипными для широкого к,ласса реща- емых задач. Это возможно благодаря тому, что при решении любой задачи маршрутного типа производится нормирование цены деления системы дуг с учетом заданных значений функций влияния, что оказывается на унификации процедуры решения задач и повышении
точности.
Такой способ подготовки планшетов позволяет не только графически определять оптимальный маршрут и затраты на каждом переходе от точ5 ки i к точке j, но и производить общую оценку затрат для выбранного маршрута путем суммирования эатратЛ. на каждом переход.1J
Работа с устройством осуществля0 ется в два этапа.
Первый этап заключается в построении псевдокоординат точек маршрута (фиг.1). С этой целью для удобства работы прозрачный сектор может быть снят с полого штифта (на фиг.2 устройство показано без сектора). С помощью линейки проводят через исходную точку маршрута и точку, выбираемую за начальную ось X, Перпендикулярно к оси X с помощью градусного лимба и второй поворотной пленки через первую точку маршрута ось Z. Далее оценивают, по какой из осей X или Z целесообразно увеличивать
5 (уменьшать) координаты псевдоточек. На фиг.2 показано: 0 - исходная точка маршрута; а - точка, принимаемая за начальную; б - одна из точек маршрута; б - псевдоточка маршрута.Для построения псевдоточки необходимо зафиксировать вторую поворотную планку перпендикулярно линейке. Подводят линейку по оси X так, чтобы начало отсчета прямой шкалы (при увеличении в
К раз координата Z) или начало отсчета обратной шкалы (при уменьшении координаты Z в 1/К раз) находилось на одной линии в прорезе второй планки. Далее, не нарушая положения линейки
0 с зафиксированной второй планкой, совмещают с помощью подвижного ползунка обрез первой планки с единицей шкалы на линейке и точкой б и фиксируют первую планку относительно пол5 зунка. После этого, сдвигая ползунок до совмещения обреза первой планки с числом на линейке, равным коэффициенту К (на фиг.2 К 5) отмечают на пересечении обреза первой планки и продольного паза второй планки псевдоточку маршрута б.
Из рассмотрения двух подобных пря- моугольных треугольников, катеты которых лежат на линиях Об, а гипотенузы образованы обрезом первой подвижной планки, видно, что псевдокоордината б в пять раз больше координаты точки б. Далее подводят начало отсчета 0 основной шкалы линейки к линии пересечения следующей точки С с осью X и производят аналогичные построения ее псевдокоординаты. В слу- чае К 1 координаты псевдоточек строят по аналогичной методике. Отличие при этом состоит лишь в использовании дополнительной шкалы с обратным направлением отсчета. Закон- чив построение псевдокоординат всех точек маршрута, переходят к второму этапу.
Второй этап состоит в непосредственном определении маршрута по псев- докоординатам. Для этого используют прозрачный сектор с оцифрованными концентрическими дугами совместно с линейкой и поворотными планками. Линейку выставляют как и при опре- делении псевдокоординат точек маршрута вдоль оси X. Далее освобождают фиксирующие элементы на обоих поворотных планках и полость штифта (являющуюся центром концентрических дуг совмещают с точкой, принятой за начальную (точка а). Перемещая сектор вокруг штифта, определяют ближайшую к центру псевдоточку маршрута. Через эту точку проходит дуга, харак- теризующая изолинию наименьших затрат. Для вычисления затрат на переход от точки, принятой за начальную, до ближайшей псевдоточки (называемой далее первой) необходимо зафик- сировать номер N ближайшей к этой псевдоточке дуги и воспользоваться формулой (13).
Для определения последующей точки маршрута необходимо, сохраняя поло- жение линейки неизменным, выставить полость штифта на первую точку и,
перемещая сектор вокруг штифта, определить ближайшую псевдоточку маршрута, которая и будет второй на маршруте. Аналогично описанному определяют затраты на переход от первой к второй точке. Изложенные процедуры повторяют до прохождения всех точек.
Общие затраты для найденного маршрута определяют путем суммирования затрат AI ; .- на каждом переходе.
Если начальная точка маршрута не задана, то она может быть определена путем решения п раз (п - количество заданных точек маршрута) аналогичных задач вышеизложенным способом, принимая последовательно в качестве начальной точки каждую из точек. Суммируя при этом общие затраты на каждом из маршрутов и сравнивая их между собой,, можно выявить маршрут с наименьшими затратами и принять его в качестве решения. При условии определения маршрута, затраты на который не превосходят заданной величины, процедура определения маршрута прекращается при выполнении этого условия, и он принимается в качестве решения.
Формула изобретения
Устройство для графического решения задач, содержащее линейку-с нанесенной шкалой, на которой расположен первый ползунок с фиксирующим элементом, на оси которого закреплена подвижная планка, о тличаю- щ е е с я тем, что, с целью унификации процедуры решения всего класса комбинаторных задач маршрутного типа на одном конце линейки расположена вторая поворотная планка с фиксирующим элементом, которая скреплена с первой планкой посредством свободно перемещающегося относительно выполненных в планках сквозных продольных пазов полого штифта, несущего на себе поворотный прозрачный сектор с оцифрованными концентрическими дугами, кроме того, линейка содержит дополнительную обратную шкалу и на одном конце лимб с градусной шкалой.
ФигЛ
г з



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для графического решения задач | 1984 |
|
SU1171810A1 |
| Устройство для решения геометрических и комбинаторных задач | 1986 |
|
SU1336038A1 |
| ПРИБОР ДЛЯ ПОСТРОЕНИЯ НАГЛЯДНЫХ ИЗОБРАЖЕНИЙОБЪЕКТА | 1968 |
|
SU211795A1 |
| Вычислительный прибор для определения установочных геометрических параметров | 1980 |
|
SU935974A1 |
| Устройство для преобразования угловых координат | 1986 |
|
SU1372334A1 |
| УСТРОЙСТВО ДЛЯ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ | 1990 |
|
RU2028667C1 |
| Прибор для построения панорамной перспективы | 1974 |
|
SU517520A1 |
| Чертежный прибор | 1982 |
|
SU1050914A2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК КЕПЛЕРОВСКИХ ТОЧЕК И РЕШЕНИЯ ЗАДАЧ В ПРОЕКЦИЯХ СФЕРЫ | 1990 |
|
RU2022357C1 |
| Прибор для построения стереопанорам | 1981 |
|
SU977220A1 |
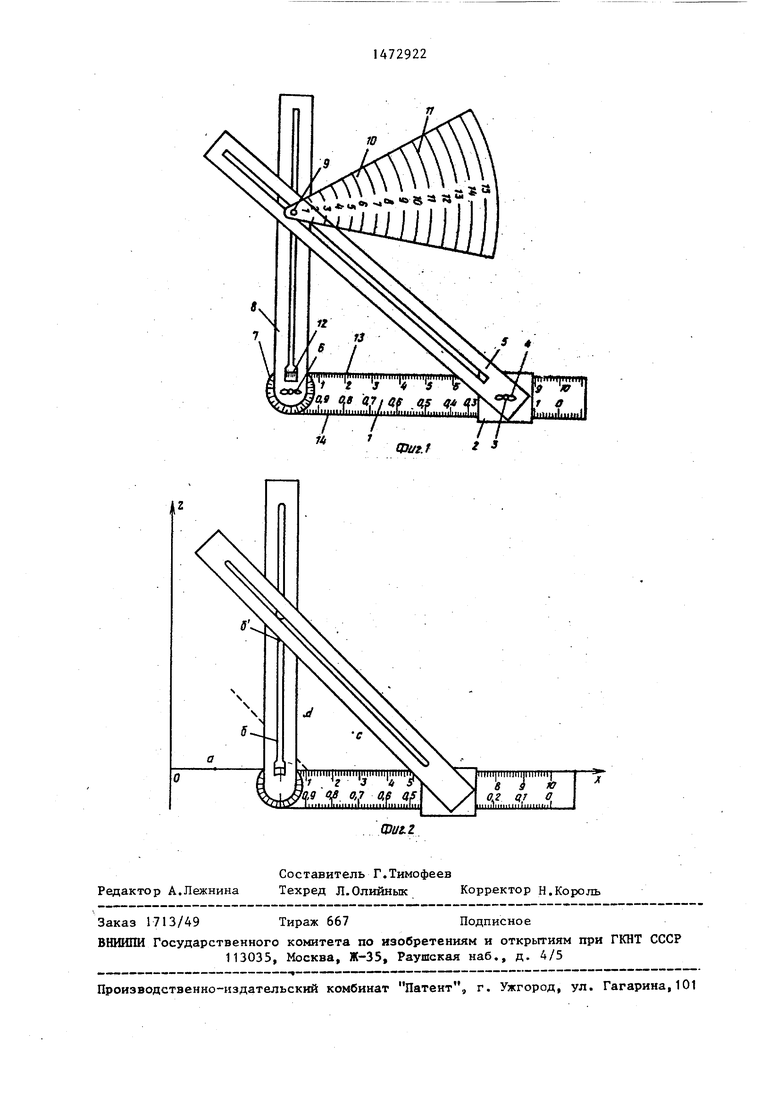
Изобретение относится к области вычислительным устройствам с ручным управлением и может быть использовано для графического решения геометрических и комбинаторных задач марштрутного типа, относящихся к классу задач коммивояжера. Цель изобретения - унификация процедуры решения всего класса комбинаторных задач маршрутного типа. Сущность изобретения состоит в применении дополнительной второй поворотной планки с фиксирующим элементом, которая скрепляется с первой посредством свободно перемещающегося относительно выполненных в планках сквозных продольных пазов полого штифта.На штифте размещается поворотный прозрачный сектор с оцифрованными концентрическими дугами. На линейке нанесены прямая и обратная шкалы, а на обрезе - лимб с градусной шкалой. Перечисленные признаки изобретения позволяют перейти от действительных координат точек маршрута к псевдокоординатам. В этом случае пространство в новых переменных будет изотропным в смысле равноценности затрат.Используя изолинии уровня затрат и эвристическое правило "идти в ближайшую точку", определяется оптимальный маршрут движения. Работа с устройством осуществляется в два этапа. На первом этапе осуществляется построение псевдокоординат точек маршрута.На втором определяется оптимальный маршрут. Используя нормирование изолиний уровня затрат, определяются общие затраты на маршруте. 2 ил.

| 1972 |
|
SU412026A1 | |
| Устройство для графического решения задач | 1984 |
|
SU1171810A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1989-04-15—Публикация
1987-07-09—Подача