д
:л
ю
ю

| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2011 |
|
RU2450436C1 |
| УСТРОЙСТВО КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2005 |
|
RU2302701C1 |
| Способ кодовой цикловой синхронизации для каскадного кода Рида-Соломона и Боуза-Чоудхури-Хоквингема [РС(32,16,17), БЧХ(31,16,7)] при одновременном применении жестких и мягких решений | 2020 |
|
RU2747623C1 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ С ЖЕСТКИМИ И МЯГКИМИ РЕШЕНИЯМИ ДЛЯ ДВУХСТУПЕНЧАТОГО КАСКАДНОГО КОДА И МОДУЛЯЦИИ ПО ТИПУ СТЫКА С1-ФЛ | 2024 |
|
RU2834891C1 |
| Способ кодовой цикловой синхронизации для каскадного кода при применении жестких решений | 2016 |
|
RU2633148C2 |
| Способ кодовой цикловой синхронизации для каскадного кода при применении жестких решений | 2021 |
|
RU2759801C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2007 |
|
RU2342796C1 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ С МЯГКИМИ РЕШЕНИЯМИ ДЛЯ ДВУХСТУПЕНЧАТОГО КАСКАДНОГО КОДА | 2012 |
|
RU2485683C1 |
| Способ кодовой цикловой синхронизации с мягкими решениями | 2017 |
|
RU2664409C1 |
| Способ устойчивой кодовой цикловой синхронизации при применении жестких решений | 2022 |
|
RU2784953C1 |

Изобретение относится к вычислительной технике и технике связи. Устройство содержит входной блок 1, блок 3 вычисления расстояний и блок 4 вычисления синдромов. Благодаря введению блока 2 декодирования кода Рида-Маллера, блока 5 совпадений, элемента ИЛИ 6 и элемента И 7 взамен более сложного блока, выполняющего итеративную процедуру Берлекэмпа, обеспечивается более надежная работа устройства. 4 ил.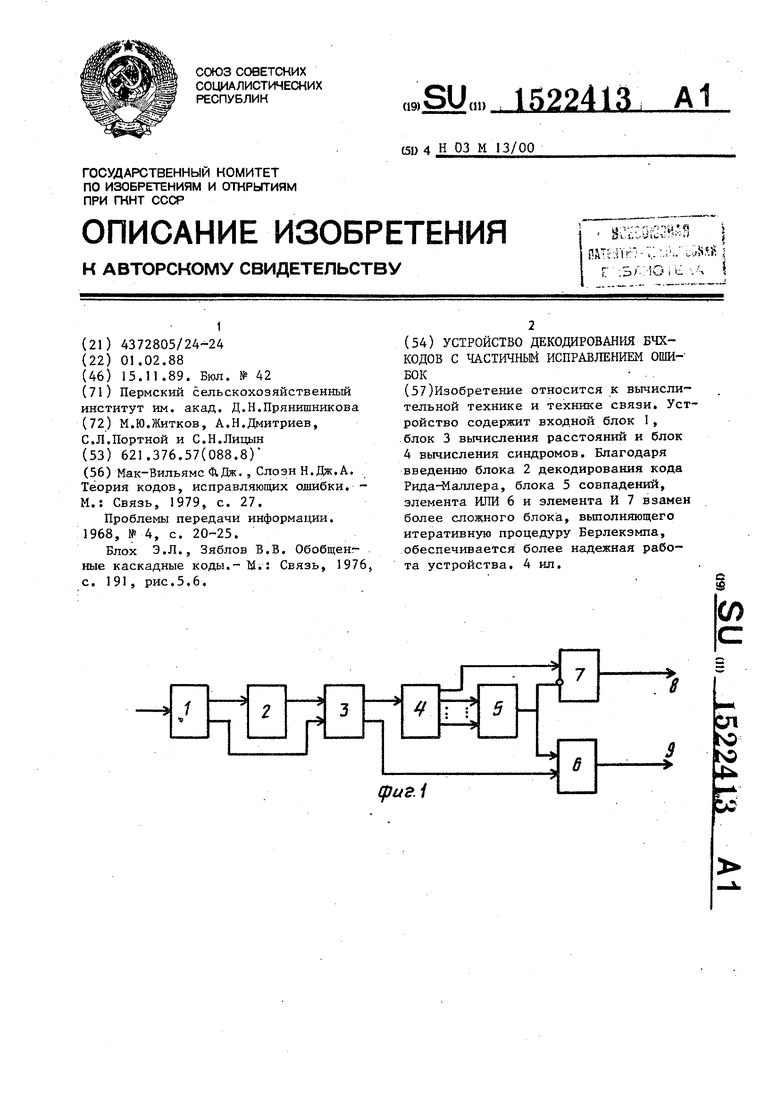
(.1
Изобретение относится к вычислительной технике и технике связи и может быть использовано в системах обработки и передачи дискретной информации .
Цель изобретения - повьшение надежности функционирования.
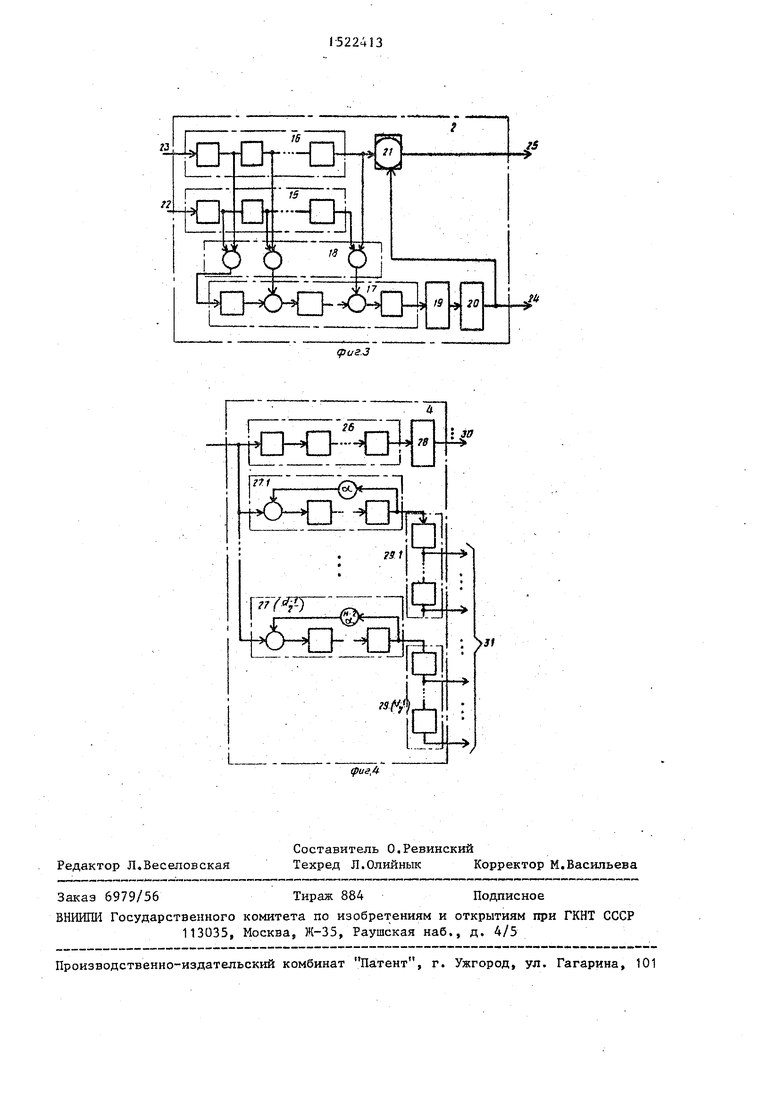
На фиг.1 приведена блок-схема устройства; на фиг.2 - схема блока декодирования кода Рида- агшера; на фиг. 3 - схема блока вычисления расстояния; на фиг. 4 - схема блока вычисления синдромов.
Устройство содержит входной блок 1, блок 2 декодирования кода Рида- Маллера, блок 3 вычисления расстояний, блок 4 вычисления синдромов, блок 5 совпадений, элемент ИЛИ 6 и элемент И 7. На фиг.1 обозначены информационный выход 8 и выход 9 отказа от декодирования .
Входной блок 1 вьшолнеи на регисре сдвига и служит для согласования скорости передачи канальных символов со скоростью работы декодирующего устройства.
Блок 2 декодирования кода Рида- Маплера (фиг.2) содержит кольцевой регистр 10 сдвига, группу 11 сумматоров по модулю два, элемент 12 задержки, мажоритарный элемент 13 и сумматор 14 по модулю два.
Блок 3 вычисления расстояний (фиг.З) содержит первый - третий регистры 15-17 сдвига , группу 18 сумматоров по модулю два, счетчик 19 импульсов,, компаратор 20 и элемент . 21 И. На фиг.З обозначены первьй и второй входы 22 и 23 и первый и второй выходы 2 и 25. В состав регистр 17 входят элементы ИЛИ.
Блок 4 вычисления синдромов (фиг.4) содержит регистр 26 сдвига, вычислители 27 синдрома, элемент 28 задержки и группу 29 регистров сдвига. На фиг.4 обозначены первый и вторые выходы 30 и 31 блока. Вычислители 27 синдромов вьшолнены на регистрах сдвига, в цепи обратной связи которых включен умножитель на элемен поля Галуа.
Блок 5 совпадений представляет собой элемент ИЖ.
Функционирование устройства основано на следуюпщх принципах.
Очевидно, если существует два код А (п, МА, ад) и В (п, MB, dft) длины п мощностей Мд и Me, с кодовыми раС стояниями с1д и dg, причем А является подкодом В (т.е. d), то любое слово, лежащее на расстоянии,не большем
0
t, . -.5от вектора кода А, алгоритмом декодирования кода В будет декодировано
Q в слово, принадлежащее коду А. Пусть R (г, т) обозначает код Рида-Маллера дпины 2 г-го порядка, а R(r, m) - код R (г, m) с одной вычеркнутой координатой.
5 Теорема. Код БЧХ длины 1 с конструктивным расстоянием d + 3 является подкодом кода R(m-3,m). Доказательство. Рассмотрим циклический код R(m-3 ,m). Как известно,
0 код R (m-3,m) задается корнями вида oi , где .двоичное представление S имеет вес Хэмминга 1 или 2, -1. Покажем, что все циклические классы, на которые разбиваются такие числа S,
5 П9рождаются представителями вида 2 + 1(,... ,tm/.23) и единицей.
Веса двоичных представителей чисел, лежащих в одном циклотомическом клас- сн по модулю 2 - 1, равны, поэтому все четные веса 2 лежат в классах с представителями вида 2 +1, где i 1,..,,m-l. Но ..
(24 1) (mod. ) + l, откуда следует, что числа 2 + 1 и
2 + i лежат в одном циклотомическом
; классе.Таким образом, циклический код
R(m-3,m)-задается корнями (/ , где
S 2 4-1, ,...,т/2Ти . По
определению примитивный БЧХ-код с .
конструктивным расстоянием + + 3 задается корнями ci/ , где ,2,. ..,2- - + 1, и так как корни, задающие БЧХ-код, содержат корни кода Рида-Маллера, то утверждение
, теоремы верно, например БЧХ-код А (63,2,11) является подкодом кода Рида-Маллера третьего порядка В (63, ).
Так же вкладываются в код R (m-3, m) и БЧХ-коды с минимальным расстоя0 нием, большим 3.
Несложно определяются и условия вложимости произвольных БЧХ-кодов в коды Рида-Маллера.
5 Устройство функционирует следующим образом.
Пусть информация передается словами кода БЧХ А (, М, d а
+ З) и требуется производить исправление до t (t З) ошибок. Искаженное слово поступает из канала во входной блок 1, с выхода которого эт слово подается на блок 3 вычисления расстояний, где сравнивается со словом, получающимся в результате декодирования принятого вектора в коде R (m-3,m) в блоке 2 декодирования кода Рида-Маллера. В блоке 3 вычисляемое расстояние сравнивается с t, и если оно больше, то на первый выход 24 выдается решение об отказе от декодирования, в противном случае слово, полученное на выходе блока 2, через второй выход 25 подается на вход блока 4 вычисления синдро- мов, в котором вычисляется синдром этого слова в коде А. Если произошло менее t ошибок, то этот синдром равен нулю, что и определяется в блоке 5 совпадений, в противном случае с выхода элемента 6 ИЛИ получается сигнал отказа от декодирования, так как с выхода блока 5 поступает единица. Если же этот сигнал равен нулю, декодированный словом, появляющимся на выходе 8, является слово, полученное на выходе блока 2 декодирования кода Рида-Малле - ;ра.
о522413
Ф о
рмула изобретения , Устройство декодирования БЧХ-ко- дов с частичным исправлением ошибок, содержащее входной блок , вход которого является входом устройства, а первый выход соединен с первым входом блока вычисления расстояний, и блок вычисления синдромов, отличаю10 щ е е с я тем, что, с целью повьш1е- ния надежности функционирования, в устройство введены блок декодирова-. ния кода Рида- аллера, блок совпадений, элемент И и элемент ИЛИ,
15 второй выход входного блока подключен к входу блока декодирования кода Рида-тМ ишера, выход которого соединен с вторым входом блока вычисления расстояний, первый и второй вы20 ходы которого подключены соответственно к первому входу элемента ИЛИ и входу блока вычисления синдромов, .первый выход которого соединен с разрешающим входом элемента И, вторые
25 входы блока вычиспения синдромов подключены к соответствующим входам блока совпадений, выход которого соединен с запрещающим входом элемента И и вторым входом элемента ИЛИ,
30 выходы которых являются соответственно информационным выходом и выходом отказа от декодирования устройства.
(Jfu.Z
Pica
4
ffii
: Vf
w
yt.
| Мак-Вильяме | |||
| , Слоэи Н | |||
| Дж.А | |||
| Теория кодов, исправляющих ошибки | |||
| - М.: Связь, 1979, с | |||
| Прибор с двумя призмами | 1917 |
|
SU27A1 |
| Проблемы передачи информации | |||
| Приспособление для контроля движения | 1921 |
|
SU1968A1 |
| Прибор для промывания газов | 1922 |
|
SU20A1 |
| Блох Э.Л., Зяблов В.В | |||
| Обобщен- | |||
| ные каскадные коды.-М.: Связь, 1976, с | |||
| Устройство непрерывного автоматического тормоза с сжатым воздухом | 1921 |
|
SU191A1 |
Авторы
Даты
1989-11-15—Публикация
1988-02-01—Подача