И
I 


| название | год | авторы | номер документа |
|---|---|---|---|
| Матричное устройство для умножения двоичных и десятичных чисел | 1983 |
|
SU1200282A1 |
| Матричное устройство для возведения в квадрат и извлечения квадратного корня | 1983 |
|
SU1107119A1 |
| Матричное устройство для умножения чисел (его варианты) | 1983 |
|
SU1160398A1 |
| Матричное устройство для возведения в квадрат и извлечения квадратного корня | 1983 |
|
SU1111155A1 |
| Матричное вычислительное устройство тригонометрических функций | 1984 |
|
SU1238060A1 |
| Матричное устройство для возведения в квадрат и извлечения квадратного корня | 1984 |
|
SU1171787A1 |
| Устройство для умножения | 1988 |
|
SU1578711A1 |
| ЯЧЕЙКА ОДНОРОДНОЙ ВЫЧИСЛИТЕЛЬНОЙ СРЕДЫ, ОДНОРОДНАЯ ВЫЧИСЛИТЕЛЬНАЯ СРЕДА И УСТРОЙСТВО ДЛЯ КОНВЕЙЕРНЫХ ВЫЧИСЛЕНИЙ СУММЫ м n-РАЗРЯДНЫХ ЧИСЕЛ | 2011 |
|
RU2475815C1 |
| Матричное устройство для вычисления тригонометрических функций | 1984 |
|
SU1226448A1 |
| Устройство для умножения с накоплением | 1986 |
|
SU1310810A1 |
Изобретение относится к вычислительной технике и может быть использовано в высокопроизводительных вычислительных устройствах. Целью изобретения является повышение быстродействия. Цель достигается за счет введения в устройство, содержащее в каждом разряде преобразователь 1 двоичного кода в код количества единиц и сумматор 3 по модулю два, доаолнительно (N+K-1) элементов И-ИЛИ 2, где N-разрядность слагаемых, K-количество входных переносов, а также новых связей. Данное устройство реализует параллельный способ суммирования и по числам, и по разрядам, вырабатывая одновременно переносы во все разряды, которые складываются на сумматорах по модулю два с поразрядными суммами. 5 ил.ю 5 табл.

&|Ц
ft
%
Щ
S
4
л №
ства единиц и сумматор 3 но модулю два, дополнительно (N+K-1) элементов И-ИЛИ 2, где N - разрядность слагаемых, К - количество входных переносов, а также новых-связей. Данное устройство реализует парал15452164
лельный способ суммирования и по числам, и по разрядам, вырабатывая одновременно переносы во все разряды, которые складываются на сумматорах по модулю два с поразрядными суммами. 5 ил.,5 табл.
Изобретение относится к вычислительной технике и может быть использовано в высокопроизводительных вычислительных устройствах.
Целью изобретения является повышение быстродействия устройства для суммирования М чисел.
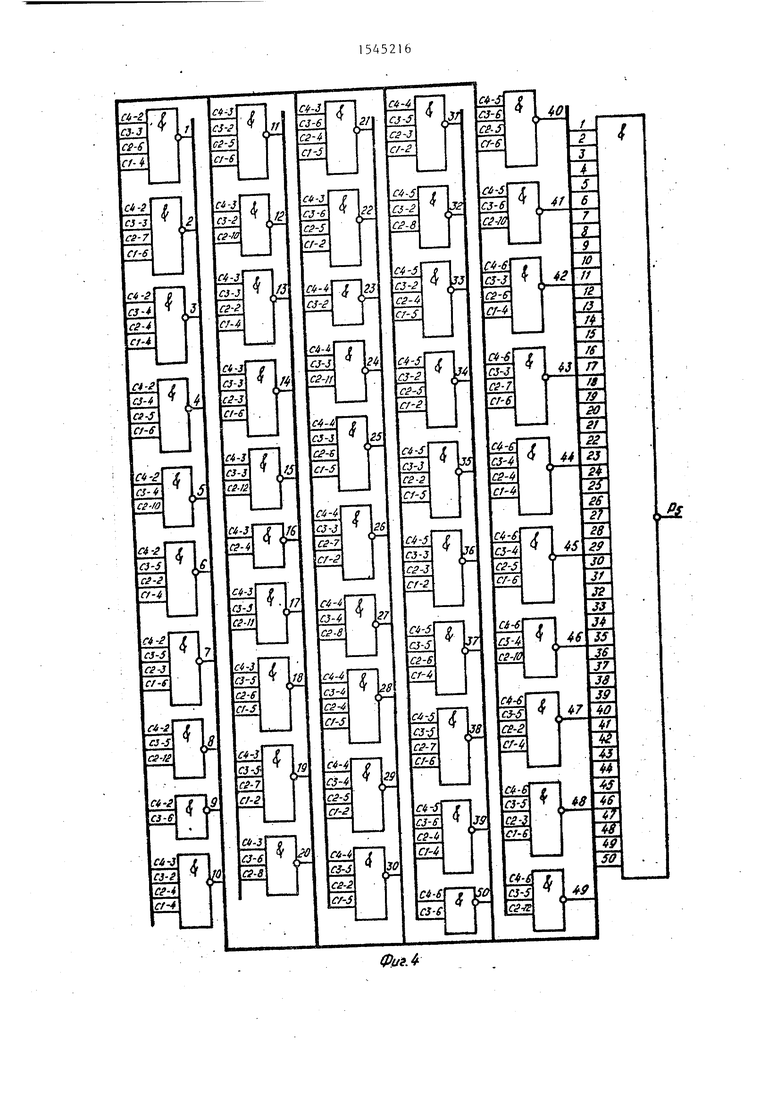
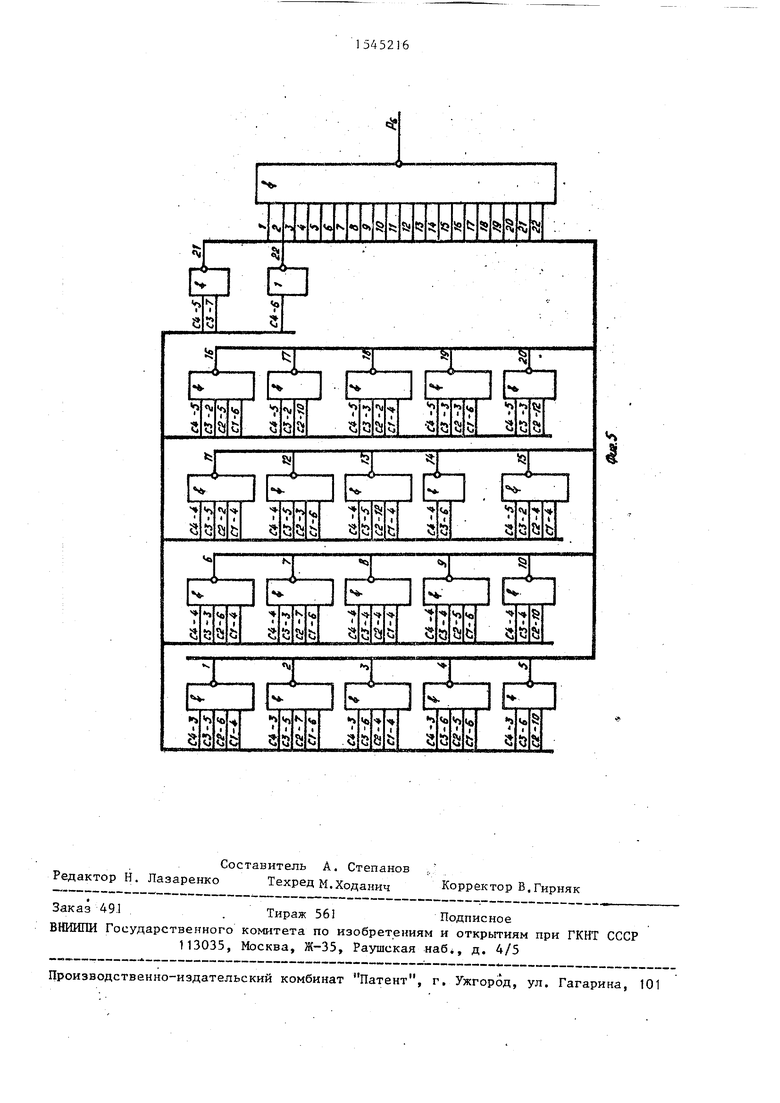
На фиг. 1 приведена структурная схема устройства, на фиг. 2-5 - четырехразрядное устройство суммирования четырех чисел.
Устройство для суммирования М чисел содержит преобразователи 1 двоичного кода0в код количества единиц, элементы И-ИЛИ 2, сумматор 3 по модулю два, входы 4 одноименных разря- дов всех слагаемых, входы 5 переноса выходы 6 суммы и выходы 7 переноса. Элементы И-ИЛИ образуют блок 8 формирования параллельных переносов P/;-PN где N - разрядность слагаемых.
На фиг. 2 показано, что с целью оптимизации элементов И-ИЛИ выходы преобразователей 1 могут быть объединены внутри преобразователя. Каждый преобразователь 1 имеет также выход нечетности кода, соединенный q входом S. соответствующего сумматора по модулю дв а.
Устройство работает следующим образом .
На входы преобразователей кодов (ПК) 1. 1-го разряда (i 14Н) поступают сигналы М слагаемых А, кроме того, на ПК 1 первых К разрядов поступают сигналы входных одноразрядных переносов Е . ПК 1 вырабатывает L . сигналов симметрических Функций, образующих совокупность С;, в том числ сигнал частичной суммы S-..Сигналы С.выходов ПК Ь поступают на соответствующие входы элементов И-ИЛИ 2, причем на элемент j-ro разряда (j 2, N) поступают определенные сигналы из совокупностей сигналов С,, ..., С; . На выходах элементов И-ИЛИ 2 образуются сигналы переносов Р во
2-ft,...,N-fi разряды, а также выходных переносов Q в (N+l)-ft,...,
(Ы+К)-й разряды. Сигналы Р,и S
i )
складываются по модулю два на сумматоре 3 по модулю два, так что на его выходе образуется сигнал результирующей суммы S,- данного разряда.
Преобразователь 1. представляет собой комбинационную схему с М+1 (если i К) либо (если i К) входами и LJ, выходами, К определяется формулой
- К-1,
MMC,KC 2
0
5
где М
1С - максимальное количество слагаемых, при котором количество выходных переносов еще равно К.
При построении ПК используют свойства симметрических функций (СФ), основным из которых является следующее: СФ m аргументов принимает значение 1 тогда и только тогда, когда в
каждом из ее
Ф
наборов аргументов
0
5
0
5
имеется ровно а единиц (символ ( )
m
означает число сочетаний из m по а), иначе говоря, значение СФ определяется только количеством а 1 в наборах ее аргументов. Число а будем называть индексом СФ.
На вход ПК I- поступают сигналы М слагаемых A j {x1f..., и входного переноса Е х„.. (для i ЈK).
М+-7,
Из этих переменных ПК I, формирует СФ вида FjCa,, aj,.. . ), аргументами которых являются индексы а , , а г, . . . , обозначим В. F | для М+l переменных Г-го разряда и Df F. для М переменных. Объединение индексов в F-, основано на следующем свойстве СФ: Р(а1, а 7, . . . ) F(a t)+F(a 7)+. . . , т.е., на возможности разложения СФ на простейшие. Простейшая СФ выражается через исходные переменные, как и обычная Функция алгебры логики, приведением к совер5154
шенной дизъюнктивной нормальной форме так при , СФ В(4) равна в(4)
,Х2Х3Х4Ху + Х,Х2Х,Х4Х + X,X,.+
Л-ХоЛ Лл
хг + х,х,х
Особым случаем функции В либо D
является СФ S- частичная сумма М - четно, то
F (1,2, .... R), т.е, i-ro разряда. Если
R
М-Н для 1,2,...,К-го разряда
М-1 для К+1 ,К+2, . . . ,
разряда
если М нечетно, то R N для всех ра рядов. Отметим, что функции S пвля- ются функциями нечетности.
Сигналы СФ, сформированные ПК 1 (i 2, К) образуют совокупность С;-. а также сигнал S1. . На выходе элементов И-ИЛИ 2 с первого по (N-1)-й фор мируются сигналы функций переноса PjPN, которые поступают на входы сумматоров 3 по модулю два с 2-г до N-ro разрядов соответственно, на выходах которых формируются сигналы результирующих сумм S { S . () Р. .
tJi Г t J Т О - О .ч.ь..«...«.
Сигнал S
формируется непосред., что упрощает схему
ственно в ПК 1
для первого разряда. На выходах элементов И-ИЛИ 2 с N-го по (N+K-1)-й формируются сигналы выходных: переносов Q,, . . ., О «.
Принцип формирования функций пере IHOCOB P и Q покажем на частном, но практически важном примере постро- ения четырехразрядного () сумматора четырех слагаемых (), у которого число К внешних-переносов равно
2 (Е,, Е q7- Г
5
V
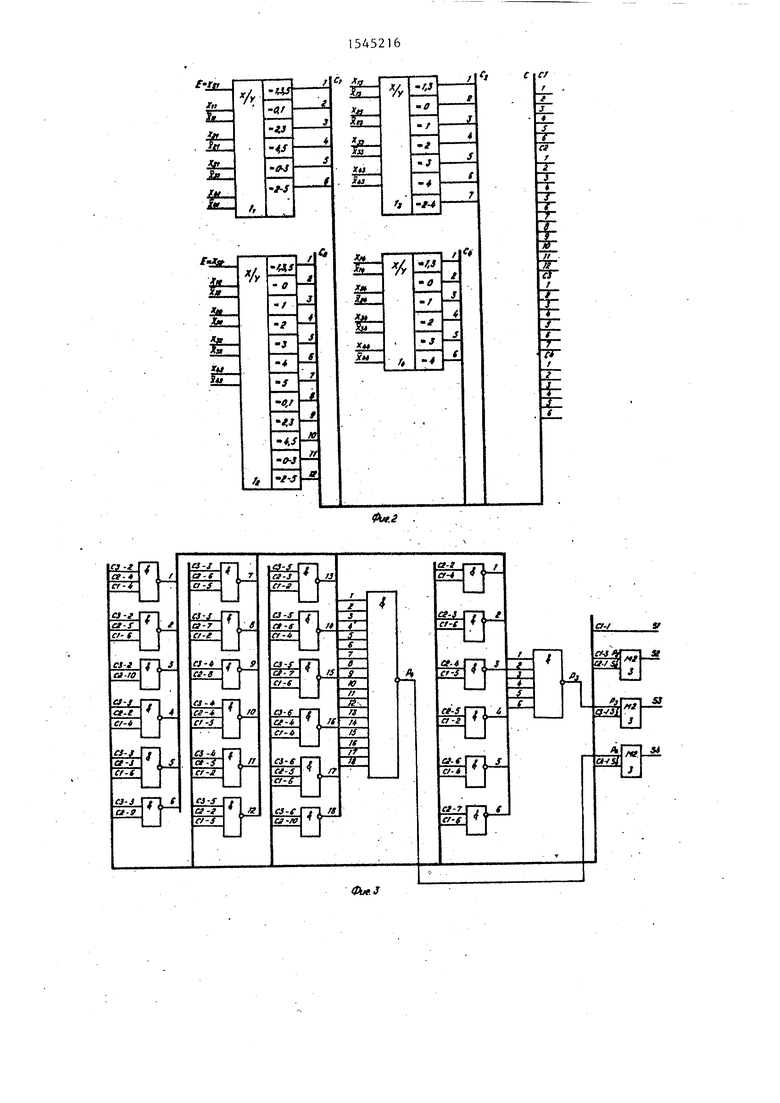
В табл.1-5 приведены значения разрядных индексов для функций переноса соответственно.
В приведенных ниже табл.-5 в столбцах помещены индексы СФ D (для третьего и четвертого разрядов) и В (для первых двух разрядов), сумма которых для Р по некоторой строке с учетом веса разряда дает перенос в i-й разряд. Например, для переноса в четвертый разряд по первой строке (табл.3) имеем 2-2 + 4-2-° 8 либо 2-21 + 5 2° 9. Аналогично составлены и остальные строки данной и всех других таблиц, так что множество строк данной таблицы является результатом перебора всех возможных вариантов получения переноса в соответствующий разряд.
О
5
0
5
0
5
0
5
«
5
66
В общем случае таблица значений разрядных индексов для Р. (2 (i f N+K) составляется следующим образом. Последовательно перебираются значения индексов от 0 до М+1 (до М для i F) в столбце первого разряда при фиксированных значениях индексов в старших разрядах, затем увеличивается на единиц значение индекса во втором разряде при фиксированных значениях индексов старших разрядов и снова производится перебор всех возможных значений индексов в первом разряде, и т,.д. до тех пор, пока во втором разряде не будут перебра Ш все возможные значения индексов, затем увеличивается на единицу значение индекса в третьем разряде и производится перебор значений индексов в первом и втором разрядах в последовательности, описанной ранее. Описанная процедура выполняется вплоть до заполнения в последнем столбце таблицы для Р.( (ко- личествр столбцов равно i-1, если i N, и равно N в остальных случаях) последнего значения индекса, равного М.
В каждой строке должны быть такие значения разрядных индексов, что их двоично-взвешенная сумма дает число, в двоичном эквиваленте которого появляется 1|: в i-м (иногда, кроме того, в (i+1)-м)разряде.
Полученные таким образом таблицы обладают некоторой избыточностью и допускают минимизацию описания схемы сумматора за счет объединения строк, в которых индексы отличаются только в одном столбце; при этом для СФ с соседними значениями индексов по данному столбцу возможно склеивание исходных переменных. Для функции В (4,5) при получаем В (4,5) х,х,х3Х4 + +х,х1х3х5 + х,х,х4х5 + xtx3x4y5 + + хгх3х4х5. Совокупность индексов 0-5 для первых двух разрядов и 0-4 для третьего и четвертого разрядов в таблицах соответствует тождественной единице, независимо от значений других переменных.
Информация, представленная в такого рода таблицах, является исчерпывающей для построения принципиальной схемы сумматора с заданными значениями М и N.
В приведенном на фиг.2 примере элементы И-ИЛИ заменены элементами
И-ПК в результата экпивалентного преобразования логических функций.
Формула изобретения 5
Устройство для суммирования М чисел, содержащее в каждом разряде преобразователь двоичного кода в код количества единиц и в каждом резряде v кроме младшего, сумматор по модулю два, выход которого является выходом суммы данного разряда устройства, входы каждого преобразователя двоичного кода в код количества единиц соединены с входами соответствующего разряда слагаемых устройства, отличающееся тем, что, с целью повышения быстродействия, устройство содержит (К+К-1) элементов И-ИЛИ. где N - разрядность слагаемых, №
к i
2 -К-1, образующих блок формирования параллельных переносов, причем каждый преобразователь двоичного кода в код количества единиц содержит выходы по числу значений кода количества единиц, а также выход нечетности кода, который в каждом разряде устройства, кроме младшего разряда, соединен с первым входом сумматора по модулю два того же разряда, выходы элементов И-ИЛИ с первого по (N-1)-й соединены с вторыми входами соответствующих сумматоров по модулю два, а выходы элементов И-ИЛИ с N-ro по (К+К-1)-й соединены с выходами переносов устройства, в каждом i-м разряде (i 2,..., JT+K) входы каждой группы И элемента И-ИЛИ соединены с выходами преобразователей двоичного кода в код количества единиц разрядов с первого по (з-1)-й для i N
и с первого по N-й для i N, так что
. ( И В ) Л 2 0, где Л- поразрядk-i 1
ная операция И; j - номер выхода преобразователя Двоичного кода в код количества единиц, j О,..., I, L - число входов преобразователя; В - вес j-ro выхода К-го преобразователя, В 0,..., L, дополнительные входы преобразователей двоичного кода в код количества единиц с первого по К-й соединены с нходами переноса устройства, выходом суммы младшего разряда устройства является выход нечетности преобразователя двоичного кода в код количества единиц этого разряда.
Продолжение табл. 4
Строка
7 8 9
10 I 1 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44
45 I
Продолжение табл.4.
р и м е ч а
н и е.
2-5; 0-3 и тчп. обозначают пере- числение индексов 2,3,4,Ь}0,1,2,3;..
40
| Устройство для суммирования @ одноразрядных двоичных чисел | 1981 |
|
SU1068932A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Устройство для сложения @ чисел | 1983 |
|
SU1159013A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1990-02-23—Публикация
1987-02-05—Подача