10
3
ф
Ю
зэ

| название | год | авторы | номер документа |
|---|---|---|---|
| Генератор случайных чисел | 1986 |
|
SU1345191A1 |
| Генератор случайных чисел | 1987 |
|
SU1495788A1 |
| Генератор случайных чисел с произвольным законом распределения | 1987 |
|
SU1509883A1 |
| Генератор случайных чисел | 1985 |
|
SU1302275A1 |
| Генератор случайных чисел | 1981 |
|
SU1008738A1 |
| Генератор случайных последовательностей | 1985 |
|
SU1327099A1 |
| Генератор случайного марковского процесса | 1989 |
|
SU1624446A1 |
| Управляемый генератор случайных чисел | 1981 |
|
SU960812A1 |
| Цифровой функциональный преобразователь | 1977 |
|
SU742947A1 |
| Цифровой фильтр | 1986 |
|
SU1354393A1 |
Изобретение относится к вычислительной технике и может быть использовано при построении имита- ционно-моделирующей аппаратуры. Цель изобретения - повышение точности формирования интегрального закона распределения вероятностей генерируемых случайных чисел. Генаратор содержит датчик 1 равномерно распределенных случайных чисел, узел 2 задания функций распределения, выполненный в виде блока постоянной памяти, узел 3 задания параметров аппроксимации, выполненный в виде блока памяти, первый и второй регистры 4-5s первый и второй блоки 6 и 7 умножения, первый и второй сумматоры 8 и 9. Цель изобретения достигается введением блоков с соответствующими связями. 2 ил..
Фиг.1
Изобретение относится к вычислительной технике и может быть использовано при построении имитационно- моделирующей аппаратуры
Цель изобретения - повышение точности формирования интегрального закона распцеделечия вероятностей генерируемых случайных чисел.
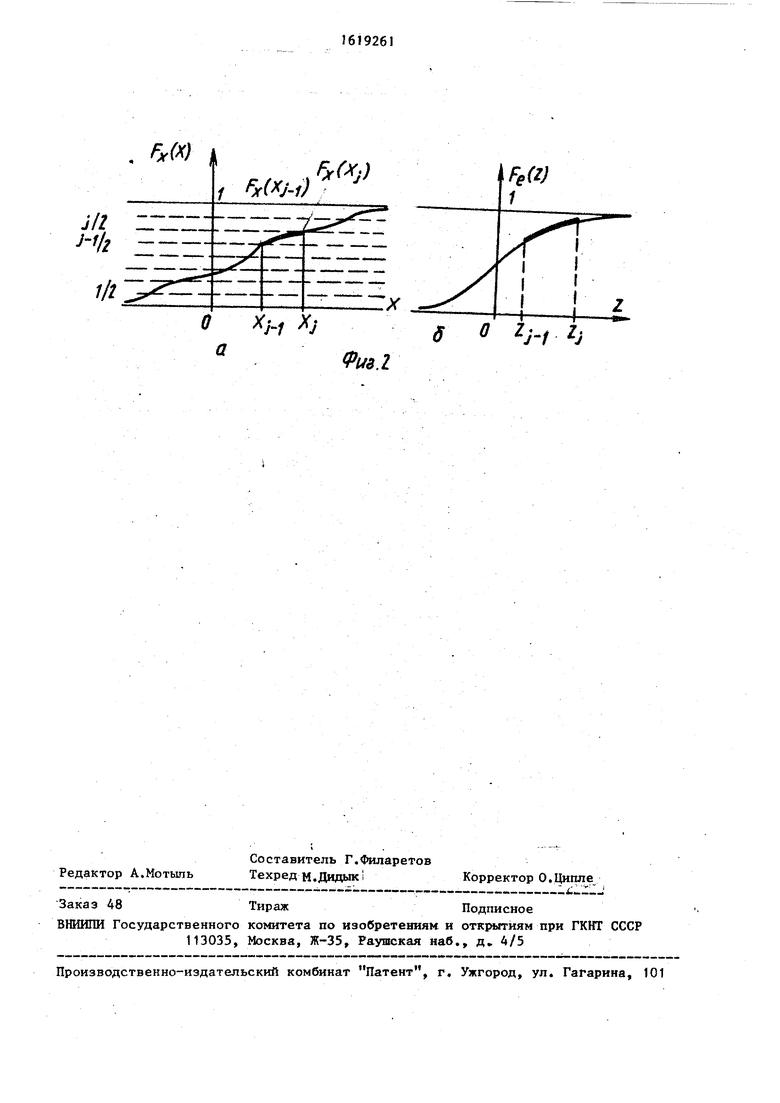
На фиг 1 представлена структурная схгма генератора случайных чисел; на фиг.2 - диаграммы, поясняющие основную идею его функционирования.
Генератор содержит датчик 1 равномерно распределенных случайных чисел , узел 2 задания функций распределения , выполненный в виде блока постоянной памяти узел 3 задания параметров аппроксима ш, также выполненный в зиде блока постоянной памяти (в этом узле может использоваться вместо бпока постоянной памяти оперативное запоминающее устройство) , первый и второй регистры 4 и 5, первый и второй блоки 6 и 7 умножения, первый и второй сумматоры 8 и 9, выход 10 второго сумматора 9 являетет выходом генератора.
Генератор работает следующим образом.
Перед началом работы генератора в блок постоянной памяти узла 2 задания функции распределения записываются значения FI (R), соответствующие функциям,обратным интегральным функциям распределения F,(Z); 1 - 1,2,... L. с помощью которых осуществляется кусочно-функциональная аппроксимация интегральной функции распределения Fx(x) формируемых случайных чисел х. Количество аппроксимирующих распределений L определяется сложностью формы Fx(x) или же желательностью использования для аппроксимации некоторого набора типовых распределений F«(x). Размер адресного поля постоянного запоминающего устройства узла 2 зависит от L, а также от количества точек дискретного представления каждой из функций Fp(R).
Предварительно функция распределения Fy(x) разбивается по оси ординат на 2К равных участков (фиг.2а) с точками разбиения i/2 ; j 1,2,...,2 -1. Тем самым определяются и точки разбиения . по оси абсцисс. Произвольная точка такого разбиения аналитически определяется с помощью соотношения Fx(xp j/2K.
0
5
0
5
Далее каждый из участков функции распределения Fj( (x) для значений аргумента xj ; j 1,2,...,2К аппроксимируют тем или иным участком одной из функций распределения Fg(),подходящим образом отмасшта- бированным с помощью линейного преобразования вида x a, + b Z.
На фиг.26 представлен аппроксимирующий участок с граничными значениями аргумента Z ,Zj .Соответствующая случайная величина Z может быть получена с помощью известного метода обратных функций из равномерно распределенных случайных чисел, если дополнительно учесть, что значения Z должны изменяться только в пределах от Z }(до Z , . Это условие может быть реализовано с помощью линейного преобразования вида R с/ + dj R, где R - равномерно распределенные в диапазоне (0-1) случайные числа, получаемые от датчика 1. Коэффициенты указанных линейных преобразований а,,Ь.,с, di; j 1,2. ,,,,2 определяются с помощью следующих соотношений:
0
а; х
.С1
bi
1- ZJ - v : .
xiZ j-(
J-
j-j.
7 i - 7 .
L V1
5
0
5
0
5
cj -Fe(ZH); dj - VZp - Fe(Zj4 ).
Найденные таким способом значенш коэффициентов aj,bj,cj,dj; j 1,2,...,2 записываются в ячейки блока постоянной памяти узла 3 задания параметров аппроксимации : с: в первую группу младших разрядов j-й ячейки; dj - во вторую группу младших разрядов; a j - во вторую группу старших разрядов; b } - в лервую группу старших разрядов. Кроме того, в средние разряды записывается номер 1 распределения F(Z), с помощью которого осуществляется аппроксимация данного участка.
Генерация очередного случаййого числа х с заданным интегральным законом распределения Fx(x) происходит следующим образом.
Датчик 1 равномерно распределенных случайных чисел вырабатывает на своих разрядных выводах новое число, k старших разрядов которого задают адрес j ячейки блока 3 пострян516
ной памяти узла. Информация, хранящаяся в j-й ячейке, считывается и переписывается в первый регистр 4: значение cV - в первую группу младших разрядов этого регистра; dj - во вторую группу младших разрядов; 1 - в средние разряды; а. - во вторую группу старших разрядов; Ь; - в первую группу старших разрядов. С младших разрядных выходов датчика 1 число R, подчиняющееся равномерному распределению в диапазоне (0-1),попадает на один из входов первого блока 6 умножения, где умножается на коэффициент dj. Получившееся произведение складывается с коэффициентом с в первом сумматоре 8, в результате чего на его выходе образуется случайное число R с + dj R. Это число переписывается в младшие разряды второго регистра 5, в старшие его разряды переписывается информация со средних разрядов первого регистра 4. Тем самым во втором регистре 5 формируется адрес ячейки блока постоянной памяти узла 2 задания функций распределения, причем старшие разряды указы вают тот адресный сегмент, где хранятся значения функции F,1 (R) , а младшие разряды - величину аргумента R. На выходе узла 2 появляется случайное число Z, которое подчиняется интегральной функции распределения Fe(Z) и может изменяться в пределах от Z I ( до Zj. Это число перемно жается во втором блоке умножения 7 с коэффициентом bJ, а затем произведение b:-Z складывается во втором сумматоре 9 с коэффициентом а;. В результате на выходе 10 образуется очередное случайное число х а| + b.- Z. Далее цикл генерации повторяется. Последовательность выходных случайных чисел х в конечном итоге будет подчиняться заданному распределению с точностью до ошибок используемой кусочно-функциональной аппрок сима- ции. Применение подобной аппроксимации во многих случаях позволяет существенно повысить точность формирования заданного интегрального закона распределения FX(X) по сравнению с
92616
известными методами, где, как правило, используется линейная интерполяция.
Формула изобретения
10
15
20
25
30
35
40
45
50
Генератор случайных чисел, содержащий датчик равномерно распределенных случайных чисел и узел задания функций распределения, отличающийся тем, что, с целью повышения точности формирования интегрального закона распределения вероятностей генерируемых случайных чисел, в него введены два блока умножения, два сумматора, два регистра и узел задания параметров аппроксимации, причем старшие разрядные выходы датчика равномерно распределенных случайных чисел соединены с информационными входами узла задания параметров аппроксимации, выход которого соединен с информационным входом первого регистра, первая группа младших разрядных выходов первого регистра соединена с первым входом первого сумматора, вторая группа младших разрядных выходов первого регистра соединена с первым входом первого блока умножения, второй вход которого соединен с младшими разрядными выходами датчика равномерно распределенных случайных чисел, а выход - с вторым входом первого сумматора, выход которого соединен.с информационными входами младших разрядов второго регистра, информационные входы старших разрядов которого соединены со средними разрядными выходами первого регистра, выход второго регистра соединен с информационным входом узла задания функций распределения, выход которого соединен с первым входом второго блока умножения, второй вход которого соединен с первой группой старших разрядных выходов первого регистра, а выход - с первым входом второго сумматора,второй вход которого соединен с второй группой старших разрядных выходов первого регистра, выход второго сумматора является выходом генератора случайных чисел.
FM
1 x(XJ-l)
fy(j)
Фю.г
Fe(z)
| Гладкий B.C., Вероятностные вычислительные модели | |||
| - М.: Наука, 1973, с,82 | |||
| Там же, с | |||
| Аппарат, предназначенный для летания | 0 |
|
SU76A1 |
Авторы
Даты
1991-01-07—Публикация
1987-12-08—Подача