Ё


| название | год | авторы | номер документа |
|---|---|---|---|
| Анализатор спектра фурье | 1979 |
|
SU800994A1 |
| Многоканальный автокоррелятор | 1979 |
|
SU817733A1 |
| УСТРОЙСТВО ДЛЯ МОНИТОРИНГА ПЕРЕХОДНЫХ РЕЖИМОВ В ЭЛЕКТРИЧЕСКОЙ СИСТЕМЕ | 2014 |
|
RU2554513C1 |
| Устройство для разложения цифровых сигналов по Уолшо-подобным базисам | 1983 |
|
SU1108461A1 |
| СПОСОБ МОНИТОРИНГА ПЕРЕХОДНЫХ РЕЖИМОВ В ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЕ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2513874C1 |
| Устройство для приема дискретных сигналов | 1987 |
|
SU1501120A1 |
| Способ имитации сигнально-помеховой обстановки | 2023 |
|
RU2818373C1 |
| Устройство для спектрального анализа | 1981 |
|
SU1013972A1 |
| Устройство для вычисления спектра Фурье | 1983 |
|
SU1121678A1 |
| Устройство для управления динамическими испытаниями | 1986 |
|
SU1361504A1 |
Изобретение относится к электротехнике и может быть использовано для определения спектральной плотности колебаний параметров режима электроэнергетических систем (ЭЭС) в темпе реального времени. Цель изобретения - повышение быстродействия. Для этого в устройстве предлагается применять метод быстрого преобразования Уолша (БПУ). Возникающие при этом искажения в спектральной плотности устраняются с помощью выбранной специальным образом матрицы преобразования. Общее время оценки спектральной плотности параметров режима ЭЭС в этом случае сокращается. 1 ил.
Изобретение относится к электротехнике, а именно к устройствам для определения характеристик параметров режима электроэнергетических систем (ЭЭС) - спектральная плотность, которая широко применяется в задачах идентификации ЭЭС как объектов управления, фильтрации и прогноза параметров режима.
Цель изобретения - повышение быстродействия устройства.
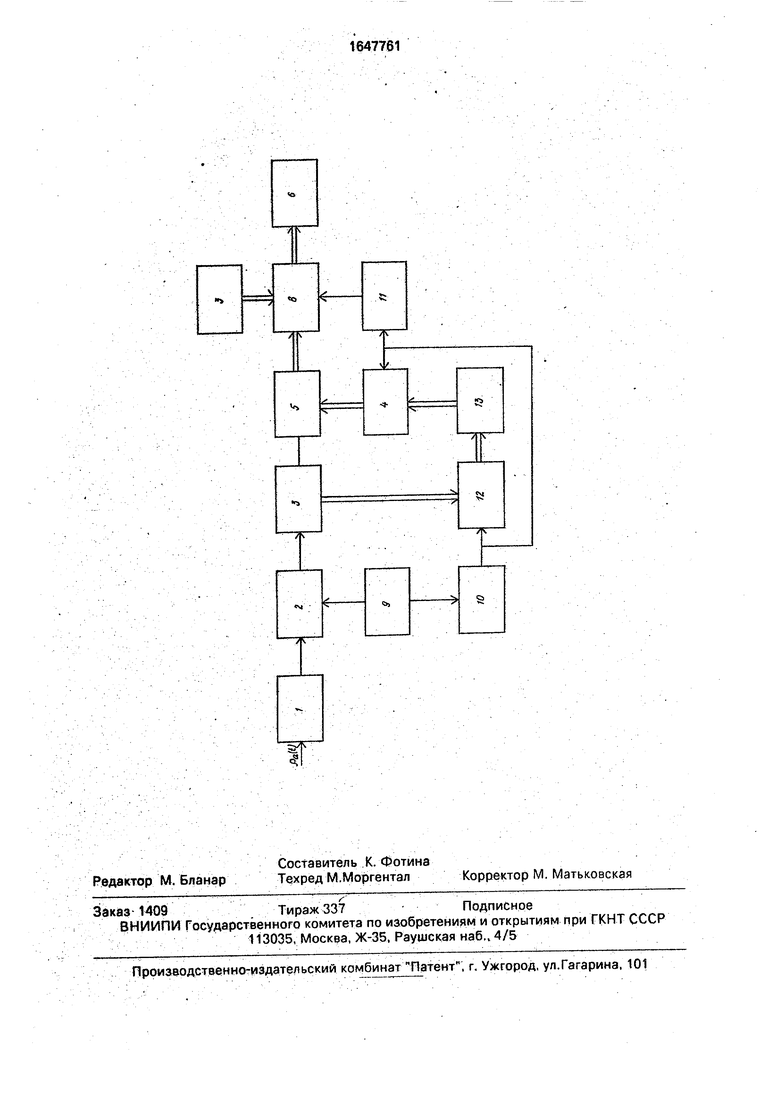
На чертеже приведена схема устройства для определения спектральной плотности параметров режима электроэнергетических систем.
Устройство содержит низкочастотный фильтр (ФНЧ) 1, аналого-цифровой преобразователь (АЦП) 2, первый блок 3 памяти, арифметический блок 4, блок 5 усреднения, блок 6 отображения 6, третий блок 7 памяти умножитель 8 вектора на матрицу, таймер 9,
первый счетчик 10, второй счетчик 11, блок 12 ключей и второй блок 13 памяти.
Выход ФНЧ 1 подключен к входу АЦП 2, информационный выход которого подключен к входу первого блока 3 памяти.
Выход таймера 9 подключен к управляющему входу АЦП 2 и к входу первого счетчика 10. Выход последнего соединен с управляющими входами блока 12 ключей, на информационные входы которого включен выход первого блока 3 памяти. Информационный выход блока 12 ключей соединен с входом второго блока 13 памяти, который в свою очередь связан с входом арифметического блока 4.
Выход арифметического блока 4 соединен с блоком 5 усреднения, который подключен к первому входу блока 8 умножения вектора на матрицу, на второй вход которого включен третий блок 7 памяти, хранящий
О
1 VJ
о
значения элементов матрицы преобразования.
Выход первого счетчика 10 соединен также с управляющим входом арифметического блока 4 и с входом второго счетчика 11, выход которого подключен к управляющему входу умножителя 8 вектора на матрицу.
Блок 6 отображения соединен с выходом умножителя 8 вектора на матрицу.
Для объяснения функционирования устройства приведены его математические обоснования. Пусть рп -р(п ЛТ)последовательность комплексных случайных величин, полученных выборкой из непрерывного комплексного случайного сигнала p(t)Ј(t) + ity(t) с частотой
Найквиста АТ ,где F - верхняя граничная частота в спектре исследуемого параметра режима р (t): (n -ДТ)(п -AT).
О)
Разложим последовательность рп для ,1,.,.,N-1 в базисах дискретных экспоненциальных функций и дискретных функций Уолша
7fg;f U(n,k);(2)
N -1
(n,k).
где РЭ (rt.k) - базисные экспоненциальные функции;
(n,k) - аналогичные функции Уолша HU;
Uk - соответствующие коэффициенты разложения в этих базисах.
Известно, что спектральные коэффициенты разложения в разных базисах связаны соотношением
Lk f ипФ(пД),(3)
п 0
1N 1
где Ф(пЛ)-(п 2 и(п,т)ь (k,m)
ядро Фурье.
Ядра Фурье составляют ортонормиро- ванную систему функций.
если m - п; если m п,
2Ф(пЛ)Ф(тЛ) {0 k 0I
(4)
Оценкой энергетического спектра S(k) последовательности рп служит
S(k)Lkl2.(5)
Усреднение в (В) выполняют либо по k, суммируя с весами соседние с Lk значения t Lk + i I2, либо суммируя с одинаковым весом соответствующие значения I Ц I2
нескольких периодиграмм. В последнем случае сохраняется высокая разрешающая способность в оценках спектра. При этом количество усредняемых периодиграмм для высокой точности оценки спектральной
плотности может достигать нескольких десятков и даже сотен. Этот способ определения энергетического спектра (спектральной плотности) является прототипом для предлагаемого способа.
Из (3) с учетом (4 ) получают
S(k) JU 1|Unf2|0(n,k)I2. (6)
n 0
0
5
0
5
0
5
0
5
Оценку | Un получают методом усреднения М периодиграмм. т.е
,м - 1
lUn|2 Ј lUn.ei2,(7)
me 0
где Un,e - спектральные коэффициенты е-й подпоследовательности /Эп . е в базисе функций Уолша.
В общем случае подпоследовательности /Эр , е составлены из/Эп и могут перекрываться во времени.
Из (6) и (7) следует, что оценка энергетического спектра S(k) в базисе экспоненциальных функций может быть получена путем усреднения периодиграмм в базисе функций Уолша и затем выполнения (однократно) преобразования (6).
Вычислительные затраты при оценке S(k) традиционным методом усреднения периодиграмм составляет -к- togaN + MN
комплексных умножений и MN logaN+MN комплексных операций сложения.
При оценке S(k) в предлагаемом устройстве вычислительные затраты составят 2N2 комплексных умножений и порядка NN log2N+N(N+M)комплексных сложений. Если время выполнения операций умножения обозначить ty , то время сложения tc можно записать в виде1с 31у, где ,1-0.3. Тогда выигрыш в вычислительных затратах составляет
MN(tog2N +Slog2N +S + 1 ) ® N N S (loga N+1)+N(S+2)
Для типичных значений , и S 0,2 получат ,4. Увеличение выигрыша вычислительных затрат достигается при уменьшении N и росте М. Так при и , ,5.
Следует отметить, что уменьшение вычислительных затрат при реализации предлагаемого устройства может быть значительно (примерно в 2 раза) выше приведенных цифр за счет учета нулевых элементов матрицы Ф (n,k). Количество нулевых элементов в этой матрице составляет порядка 70%, т.е, матрица Ф(п,1) является слабозаполненной.
Таким образом, для типичных значений количества усредняемых реализаций М и их длительности N выигрыш ©в вычислительных затратах в предлагаемом способе по сравнению с известным составляет от двух до пяти.
Предлагаемое устройство функционирует следующим образом.
На вход ФНЧ 1 поступает сигнал анализируемого параметра режима (t), а на выходе формируется отфильтрованный сигнал р(и) с полосой частот 0,F, в которой измеряется спектральная плотность. АЦП 2 с шагом AT -ryr измеряют значения процесса
и заносит их последовательно в ячейки памяти блока 3 памяти. Если блок 3 памяти выполнить в виде большого регистра сдвига, то значения рп достаточно записывать в первую ячейку этого блока. Команды для управления АЦП 2 формирует таймер 9 с шагом Л Т, т.е. таймер 9 - это обычный генератор импульсов с интервалом AT.
Импульсы таймера 9 подсчитываются в первом счетчике 10, пороговое значение которого равно , ,2... Когда первый счетчик 10 заполняется, он выдает разрешающий сигнал блоку 12 ключей, и накопленные в первом блоке 3 памяти значения
-р( п ДТ ), ,1N-1 записаны во
второй блок 13 памяти. Одновременно выдана первым счетчиком 10 команда на запуск арифметического блока 4. В этом блоке осуществляется нахождение дискретного преобразования Уолша (ДПУ) методом быстрого преобразования Уолша и определяются квадраты модулей найденных коэффициентов. От запускающего сигнала также срабатывает второй счетчик 11, который считает количество усредненных реализаций.
С выхода арифметического блока 4 квадраты модулей коэффициентов Уолша усредняются в блоке 5 усреднения. В этом блоке осуществляется обычное накопление значений несглаженной спектральной плотности в базисе ДПУ для каждого значения частоты.
Приведенная процедура осуществляется многократно (заданное число раз М), пока не переполнится второй счетчик 1, который при этом выдает управляющий сигнал блоку
8 перемножения вектора на матрицу. Значения компонент вектора поступают с выхода блока 5 усреднения, а элементы матрицы преобразования (с учетом нормирующих коэффициентов) хранятся в третьем блоке 7
памяти. Блок 6 отображения обычно произвольный, но должен быть удобным для пользователя. Это обычно цифровой индикатор, дающий результаты измерений в виде таблицы, либо дисплей, позволяющий отображать информацию о спектральной плотности в виде таблиц, графиков, гистограмм и т.д.
Все используемые в предлагаемом устройстве блоки являются стандартными. Наиболее сложный арифметический блок представляет собой последовательно соединенные устройства для нахождения ДПУ, два квадратора и сумматор.
Связи между блоками показаны двойными линиями и являются связями типа шина, т.е. являются многопроводными
Формула изобретения Устройство для определения спектральной плотности колебаний параметров режима электроэнергетических систем, содержащее блок отображения и последовательно соединенные фильтр нижних частот, аналого-цифровой преобразователь и блок памяти, а также арифметический блок,
подключенный к блоку усреднения, отличающееся тем, что, с целью повышения быстродействия устройства, арифметический блок выполнен в виде блока определения квадратов коэффициентов Уолша и в
устройство дополнительно включены последовательно соединенные таймер, первый счетчик, блок ключей и второй блок памяти, выход которого соединен с входом арифметического блока, а также второй счетчик,
третий блок памяти и перемножитель вектора на матрицу,первый вход которого подключен к выходу блока усреднения, второй вход соединен с третьим блоком памяти, управляющий вход подсоединен к выходу
второго счетчика, а выход подключен к входу блока отображения, причем выход первого счетчика соединен с управляющим входом арифметического блока и с входом второго счетчика, а второй выход таймера
подключен к управляющему входу аналого- цифрового преобразователя.
| Орнов В.Г | |||
| и др | |||
| Задачи оперативного и автоматического управления энергосистемами | |||
| -М.: Энергоатомиздат, 1988 | |||
| Рабинер Л | |||
| и др | |||
| Теория и применение цифровой обработки сигналов | |||
| - Мир, 1978 |
Авторы
Даты
1991-05-07—Публикация
1989-02-27—Подача