Изобретение относится к измерительной технике и может быть использовано для контроля точности изготовления изделий сферической формы, например, судовых и авиационных изделий, элементов паровых котлов и реакторов, сферических зеркал и экранов кинескопов.
Цель изобретения - повышение точности и производительности определения геометрических параметров и расширение области применения способа.
На фиг. 1 показана схема определения геометрических параметров сферической поверхности изделия; на фиг. 2 - схема разметки сферического сегмента; на фиг, 3 - то же, с отверстием на полюсе.
Схема содержит контролируемую поверхность 1, сферическую поверхность 2 номинального радиуса R с центром 0 и узловую сферическую поверхность 3 с цен- тром Oi.
Способ осуществляют следующим образом.
С помощью трафарета осуществляют разметку контролируемой поверхности 1 так, что измеряемые точки распределяются по поверхности 1 с учетом удобства определения их координат и относящихся к ним элементарных площадей. При выборе числа точек учитывают размеры и форму по- верхности 1. Каждая измеряемая точка размещается в центре своего участка. Определяют площади соответствующих участков разметки. При контроле полных сфер или сферических сегментов площади участков определяют по формуле
dS R2 5 пвдвд р,
где в и р - соответственно угловые координаты точки на поверхности 1.
При контроле сферических сегментов 4 и 5 (фиг. 2 и 3) измеряемые точки располагают на пересечении равноудаленных меридианов и параллелей. Крайние параллели совмещают с краями сферического сегмента 5 и его отверстия. Затем определяют отклонение д от сферической поверхности 2 номинального радиуса R с центром 0, вы- бранным произвольно вблизи истинного центра От контролируемой поверхности 1. Центр Oi является центром узловой сферической поверхности 3. По результатам измерений определяют координаты центра Oi сферической поверхности 3, ее радиус РФ и величины отклонений кон- тролируемой поверхности 1 от сферической поверхности 3 в измеряемых точках с помощью следующих математических соотношений:
R + д(в,р) X slntf ) + Y slnfl sirvp + + Z cosfl + R + A Ro + A R (0,y), (1)
где 6(9,р) - измеренное отклонение радиуса контролируемой поверхности 1 для произвольной точки;
X.Y.Z - искомые координаты истинного центра контролируемой поверхности 1;
ARo - искомое отклонение фактического среднего радиуса контролируемой поверхности 1 от номинального;
AR(0,y) - искомое отклонение контролируемой поверхности 1 от сферической поверхности радиуса R0 для произвольной точки;
Оф - угловые координаты произвольной точки на контролируемой поверхности 1.
Из выражения (1)
A R (в,р) д(в,(р) - X sin0cosp - + Ysin0sinp-Zcos0-ARo.(2)
Указанные искомые величины могут быть найдены с использованием метода наименьших квадратов, согласно которому должен обеспечиваться минимум функционала:
F /(AR(0,p)fds,(3)
S
где dS - элементарная площадь поверхности;
F - обращается в минимум, если:
ЭР ЭР ЭР ЭР о щяяз
или
( 0:
/ ARM3lAR d6-o: / ARMM|MdS-o;
«ЗДЗДр-з-
l g -sinecc . iIA)l -sin0sin
от
ajAR(M--id(ARo)
После подстановки в (4): lnARo+ I12X+ liaY+ lnZ FI;
l2lARo+ I22X+ I23Y+ I24Z - F2; (5)
l3iAflo+ I32X+ 1ззУ + UZ - Рзг l4iAR0+ l«X+ UaY + l«Z -
(4)
где
In -l42 /slnflcospdS; s
li2-/sln20cosVdS;
li3-/s n20coSy dS; s
114 -/slnflcospdS;
121 l43/sln0siny dS;
122 / sin2 в siryj cos p dS;
s
l23 /sln20sinVdS; s
I24 / sln0 cos в sin (p dS; s
131 U4 / cos в dS;
s
sln0 cos 0 cosy) dS;
133 /sln0cos0siryjdS;
s
l34 /cos20dS;
s dS;
s Fi (B,p) sin 0cos p dS;
s F2 /(5 (0,p) sin в sin p dS;
(5(0,p)cos0dS;
S
344 5Z Sin 0; cos 0; s .nqi; л5; 5
Э„-3,4-21 «в 8; ft 5Г, 3j2-1 ;n8iC059;COSg ; b5; J j Sb -nOiCOSQ; 6;nlf;6S;}(6)
I.
tI
F Ј;s;ne;cosU jft5; 5
Fj-SfjSinQj SinCf, u5; j
Fs iCoeeiuSsjRt- ijaS;, где AS - площадь поверхности, отнесенной к соответствующей точке измерения. 15 Если точки по поверхности распределены равномерно и площади A S одинаковы, то
10
20
25
30
V3u-2sil0;C05cf j 7rt-2 ,C032C|; у Sin2e;5;ntp;co5Cf; -} м -2Г Si 9; COS S. cos If; } Z, - 34J-Ss;n0, Sin C/; J Ujj S Sin 6 Sin Lf COS Cf; j „-Ssin QjSln7 ;- J 21 Sin 0,006 6; SlnCf; J
V 2cose:i
3M 25in в; COS 9; COSCf, j Зл S Sin 9;co5 9; Sin Cf; , Эм-2ес9§в;;
C7J
Ut-N,
(0.)dS;
s
Величины X, Y, Z и A R (#,y) находятся из системы уравнений (5).
. При конечном числе точек I и произ- «i. вольном их расположении на поверхно- 35 где N-число точек измерения сти 1:„. л
A R. 5i - Xsln6| cos - Y sln6| slop,-Fi - dt sin « cos p
- Z cos fl - A Ro,p2 - Уй sln ft sin щ
rfleARi AR(a,$a),4° F3-5)4cos6l: . (ft.i)-T r И «pi - угловые координаты точек.Такое Разбиение контролируемой по- При этом 1,Н41 и F,-F4 могут быть замене- ерхности изделия удобно, когда она в планы суммами. Возникающая погрешность45 в ИМбеТ ПРЯМ°УГОЛЬНУЮ °РМУ- напРимвР
w кпян кинескоп и
тем меньше, чем большее число точек изме- мчпв.ииив.
В тех случаях, когда производится гон Чроль замкнутой сферы или сферического сегмента (фиг.2 и 3), точки изменения удобно располагать на пересечении равноуда- 5Q ленных меридианов и параллелей. В этом случае в формулах (6) следует принять
рений принято:
« 4а 5б п0;соэМ ;Л5; 1 1
3it-2Zs;n20;cosa(|.,-a5;) 3,3- Zl5in20;e;TiC|;cosCf;A5; i
f
1 (4 S Sin 0; COS S; COS tf; & 5; ) 45e «tne;5 ncf; 65; v
i
2z 5;n29;5inq ;cosq ; &6; ) лб;
A$ R25ln6|A0Ay
ее Крайние параллели совмещаются с краями сферического сегмента и отверстия. Тогда в системе (5)
Hi Il3- Il4 121- 122 124 (32
- 1зз- 142- 143 0; 112-1/2(1/4 l34-Ui);
344 5Z Sin 0; cos 0; s .nqi; л5; 5
Э„-3,4-21 «в 8; ft 5Г, 3j2-1 ;n8iC059;COSg ; b5; J j Sb -nOiCOSQ; 6;nlf;6S;}(6)
I.
tI
F Ј;s;ne;cosU jft5; 5
Fj-SfjSinQj SinCf, u5; j
Fs iCoeeiuSsjRt- ijaS;, где AS - площадь поверхности, отнесенной к соответствующей точке измерения. Если точки по поверхности распределены равномерно и площади A S одинаковы, то
V3u-2sil0;C05cf j 7rt-2 ,C032C|; у Sin2e;5;ntp;co5Cf; -} м -2Г Si 9; COS S. cos If; } Z, - 34J-Ss;n0, Sin C/; J Ujj S Sin 6 Sin Lf COS Cf; j „-Ssin QjSln7 ;- J 21 Sin 0,006 6; SlnCf; J
V 2cose:i
3M 25in в; COS 9; COSCf, j Зл S Sin 9;co5 9; Sin Cf; , Эм-2ес9§в;;
C7J
Ut-N,
«i. N-чис „
A$ R25ln6|A0Ay
Крайние параллели совмещаются с краями сферического сегмента и отверстия. Тогда в системе (5)
Hi Il3- Il4 121- 122 124 (32
- 1зз- 142- 143 0; 112-1/2(1/4 l34-Ui);
l3i- 1/2(r,os20i-cos2&); Ы-4/3(cos30i -cos30o):
141 - COS 01 - COsftj)
где 0 и во - углы, характеризующие положение границ меридиана, отсчитываемые от точки, принятой за полюс; для сферы сферического сегмента без отверстия на полюсе 01 0.
Интегралы Fi-F4 могут быть вычислены любым приближенным способом, например, по правилу трапеций. С учетом сказанного из системы (5) получают
4,9 2Гг
„ е z,
Tn TTJ Ч-f
о з.-з (8ч
« э„эи-з;.4 w
.-#- i (9)
„ ,-212 519511 9.,ee i|:;.t j( J
-yfsJn iSbR.jcosQj vsin fl.iR cosqj)
Z:i ZlZ:4R;ibin1e,-s;nCfi- ;-i |.i JJ
I n
-s( 6, S4fi,:5inC|: t j--t J
in g.ZTAR aingi-,
Sj-ZSuRjjsmeoj 1M
-J(s;«2Q;Ј4R,j.5ine9,z:uRMj)) (Ю)
N Я
T j«i J
-1г(.%«в|ЈйЯ1Ив.пввЈлКт.)ftRij-J.puR.-xsmO.costl; - -YsmQ, sin4j - cos6;
где:
m - число точек на меридиане, включая края сферы или полюс;
n - число меридианов,
Л0 ;Ду, 360,
m -1 т n
A RIJ - отклонение контролируемой п,о- верхности в точке IJ от сферической поверхности радиуса Яф;
I - номера точек на меридианах; J - номера меридианов.
Формула изобретения Способ определения формы сферической поверхности изделий, заключающийся в том, что фиксируют изделие в рабочем пространстве измерителя линейных перемещений и определяют координаты контролируемых точек на измеряемой поверхности относительно центра поворота измерителя, а по этим координатам вычисляют координаты центра, погрешности формы и средний радиус измеряемой поверхности, отличающийся тем, что, с целью
повышения точности и производительности определения геометрических параметров и расширения области применения способа, перед измерением осуществляют разметку измеряемой .поверхности путем
разбиения ее на участки по числу контролируемых точек,, которые располагают преимущественно в центрах участков, определяют площади соответствующих участков разметки, которые учитывают при
определении координат центра, погрешностей формы и среднего радиуса измеряемой поверхности.


| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ДИСТОРСИИ В ИНТЕРФЕРОГРАММЕ ОПТИЧЕСКОЙ АСФЕРИЧЕСКОЙ ПОВЕРХНОСТИ | 2021 |
|
RU2773806C1 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2011 |
|
RU2489083C2 |
| СПОСОБ ИЗМЕРЕНИЯ КООРДИНАТ ЦЕНТРА И РАДИУСА ЦИЛИНДРИЧЕСКИХ УЧАСТКОВ ДЕТАЛЕЙ | 2014 |
|
RU2581384C1 |
| ПОВЕРХНОСТЬ ЛИНЗЫ С КОМБИНИРОВАННЫМИ ДИФРАКЦИОННЫМИ, ТОРИЧЕСКИМИ И АСФЕРИЧЕСКИМИ КОМПОНЕНТАМИ | 2008 |
|
RU2496450C2 |
| Спектрограф | 1987 |
|
SU1522046A1 |
| Способ измерения кривизны внутренней поверхности экрана кинескопа | 1986 |
|
SU1415031A1 |
| Способ обработки сложных поверхностей | 1986 |
|
SU1393548A1 |
| Измерительный преобразователь поперечных компонент пульсаций скорости потока | 1984 |
|
SU1223150A1 |
| Способ точения некруглых в попереч-HOM СЕчЕНии ТЕл | 1977 |
|
SU818752A1 |
| СПОСОБ И УСТРОЙСТВО ОПРЕДЕЛЕНИЯ КООРДИНАТ ОБЪЕКТОВ | 2012 |
|
RU2513900C1 |
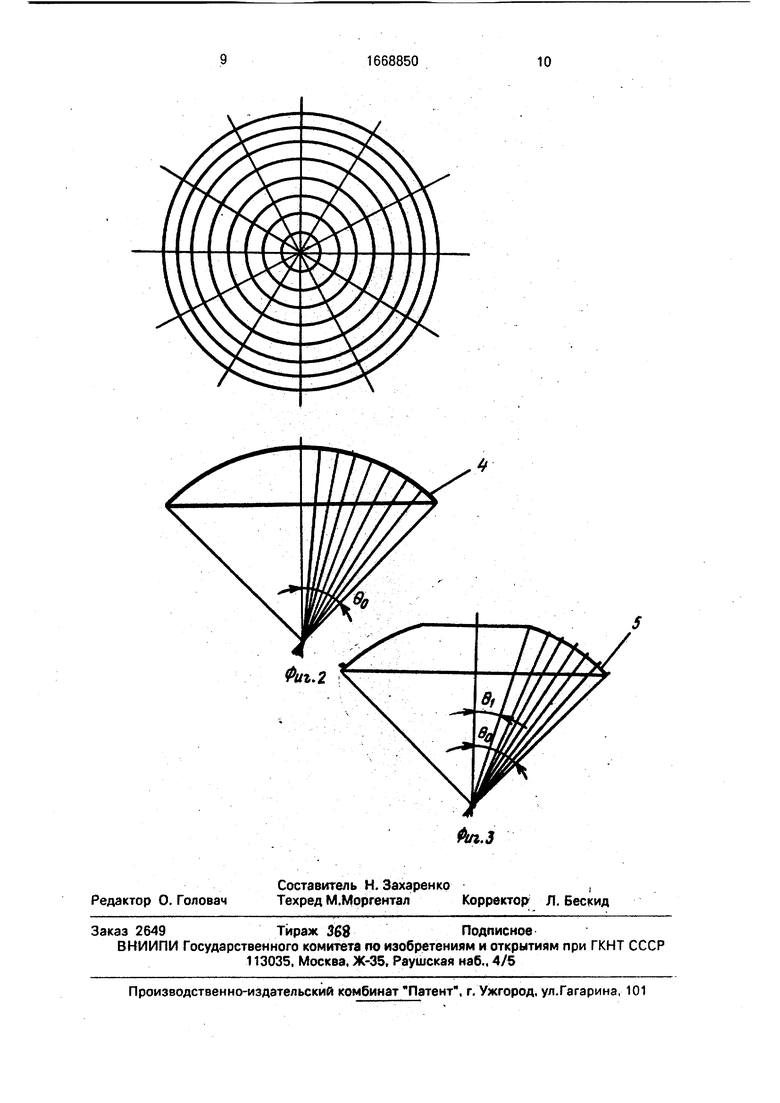
Изобретение относится к измерительной технике и может быть использовано для контроля точности изготовления изделий сферической формы, например судовых и авиационных изделий, элементов паровых котлов и реакторов, сферических зеркал и экранов кинескопов. Целью изобретения является повышение точности и производительности определения геометрических параметров и расширение области применения способа за счет выполнения разметки контролируемой поверхности и измерения площадей соответствующих участков разметки. При измерении с помощью трафарета размечают контролируемую поверхность 1 и определяют площади соответствующих участков разметки. Затем определяют отклонения δI контролируемой поверхности 1 от сферической поверхности 2 номинального радиуса в измеряемых точках, размещенных в центрах участков разметки. По результатам измерений определяют координаты центра о1 сферической поверхности 3, ее радиус Rф и величины отклонений контролируемой поверхности 1 от сферической поверхности 3 в измеряемых точках. 3 ил.
Фиг.2
| Способ измерения кривизны внутренней поверхности экрана кинескопа | 1986 |
|
SU1415031A1 |
| кл | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1991-08-07—Публикация
1989-06-15—Подача