Изобретение относится к вычислительной технике и предназначено для использования в ЭВМ и спецпроцессорах с системой команд высокого уровня, ориентированной на класс логико-комбинаторных задач.
Цель изобретения - повышение быстродействия устройства для арифметического разложения симметрических булевых функций (с.б.ф.).. ч
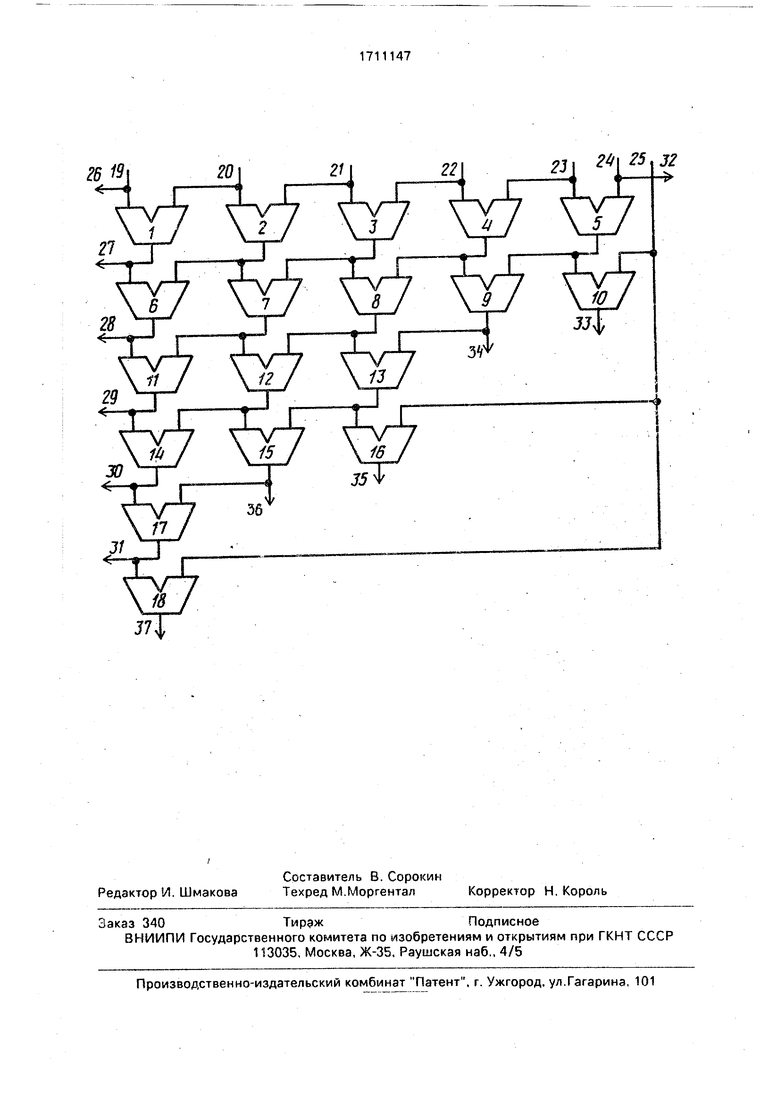
На чертеже представлена схема устройства для арифметического разложения с.б.ф. при п 5.
Устройство содержит п-2(1-1) вычитателей 1-5 первой группы, п-2(1-1)вычйтатеяей 6-10 второй группы п-2(2-1) вычитателей 11- 13 третьей группы, п-2(2-1) вычитателей 14- 16 четвертой группы, п-2(3-1) вычитатель 17
(пятой группы, п-2(3-1) вычитатель 18 шестой группы, п+1 входов 19-24, вход 25 константы логического нуля, выходов 26-31 первой группы, п+1 выходов 32-37 второй группы. .
Пусть (xi. Х2,.., хп) - с.б.ф. п аргументов Х1, Х2Хп И Л(т) (ЛЬ, Л1, .... Лп) двоичный код f. где Л - значение f на (любом) наборе значений п аргументов с i единицами. N0,1. ... п. Поскольку f - с.б.ф.. то в ее арифметической Полином G(f) аргументы xt, ха хп входят симметрично.
Следовательно, полином G(f) однозначно задается (п+1)-разрядным вектором р (F) (/оь./91, ,../Эп),тде/Oi - целочисленный коэффициент, приписанный (всем), слагаемым ранга I полинома G(f). ,1п. Вместе с
&ь
VI
тем для с.б.ф. f существует еще один арифметический полином H(f). в котором все аргументы XL Х2хп поляризованы отрицательно
(считается, что в полиноме G(1) аргументы поляризованы положительно), т.е. аргументы XL X2,..., хп входят в H(f) только с отрицанием. По аналогии с G(f) полином H(f) также может быть однозначно задан (п+1)разрядным вектором A(f) (Ao,AiАл),
причем область определения целочисленных коэффициентов AJ совпадает с областью определения коэффициентов р и имеет место
р} 2 IAH 2 где .1п.
Полиномы G(f) и H(f) в общем виде можно записать следующим образом:
G(f) РО +p (xi+X2+.,.+xn)+
pi (Х1Х2+...+Х1Хп+Х2ХЗ+..,+Хп-1Хп)+...
+ РП xix2...xn;
H(f) Яо +Я1 (X1 + X2 + ...+Xn)+ +Я2(...+MXn+X2XЗ+...+Xn-1Xn)... + Ял Х1Х2...ХП .
Поскольку арифметические полимоны G(f) и H(f) однозначно определяются векторами p(f)(A.pi/On)и Я(т) (Яо,AtЯп),
то задача арифметического разложения с.б.ф. f сводится к qpeo6pa30BaHMio вектора я(т) в векторы р (f) и Я (f).
Указанные преобразования заключаются в формировании последовательности векторов В°, . где В° я(т), а значения компонент вектора вЦ( /4.)
вычисляются по формуле
/ o /r+1i-/r1. -
где ,1n-j; ,2п.
Тогда
./&$,$$)
И Я(() (/38 + 1. ДЛ/$ - 1, , .лЙ)|(1)
где
/3S . если п четное ; . если л нечетное.
Пример. Пусть и с.б.ф. (xi, X2, хз, задана вектором я (f)(0,1, 1,0, 1). Последовательность векторов имеет
вид .
в0 - (0.1, 1,0. 1): В1 {1,0, -1,1): - В2 (-1,-1,2); 1 (0,3); В4 (3).
0
5
0
г
Векторы В , В В образуют треугольную таблицу с основанием К, которая для данного примера имеет вид
ро 0 1 1 0 1 АО р 1 0 -1 1 AI
/32 -1 -1
/5з 0 3 Аз
р4 3 Яг)
Отсюда следует, что р (f) (0,1, -1, 0.3): Я(т) (1,-1,2,-3.3). Следовательно,
G(f)(x1+x2+X3+X4)-(x1x2+X1X3+X1X4+
+ Х2ХЗ+Х2Х4+ХЗХ4)+Зх1X2X3X4: H((xi+X2+X3+X4)+2(xiX2+x1x3+ + Х1Х4+Х2ХЗ+Х2Х4+ХЗХ4)- 3(Х1Х2ХЗ+ + X1X2X4-)-X1X3X4-fX2X3X4)+3x 1X2X3X4.
5
0
5
0
5
0
5
Устройство работает следующим образом.
На 1-й (,2п+1) вход устройства подается (1-1)-я компонента JTj-i вектора (f) разлагаемой функции (xi. X2,..., хп). На выходах первой группы формируются компоненты вектора р (f). на выходах второй группы - компоненты вектора Я (f).
Так, если на входы 19-25 устройства подать соответственно компоненты ль ... Л5 вектора тг(т)(0,1.0,1.1,0). на выходах 26- 31 первой группы формируются соответственно компоненты ро ...рь вектораp(f)(0,1, -2,4, -7,10), на выходах 32-37 второй группы - соответственно компоненты АО ... Яв вектора Я(т)(0,1,-1.0,3,-10).
Разрядность вычитателей определяется числом разрядов, необходимых для представления максимально возможного по аб- солютной величине коэффициента арифметического полимона. Тогда с учетом знакового разряда разрядность вычитателей равна п+1. Причем для представления операндов (данных с промежуточных вычислений или окончательных результатов) используется дополнительный код, который формируется автоматически при условии блокирования, сигнала заема из старшего (знакового) разряда вычитателей.
Следовательно, на входы вычитателей первой группы подан (п+1)-разрядный код 00...07Г1. в котором первый (старший) разряд знаковый. На выходе этих вычитателей числа (положительные и отрицательные) уже представлены в дополнительном коде. Здесь используется тот факт, что результат выполнения операций вычитания над дополнительными кодами чисел всегда дает разность, представленную в дополнительном коде, если заем из знакового разряда заблокирован (не используется).
В каждой четной группе использованы дополнительные вычитатели, на входы уменьшаемого которых подаются сигналы логического нуля, т.е. (п+1)-разрядные коды
000. Назначение этих вычитателей состоит в изменении знаков соответствующих коэффициентов согласно (1)
Пример процесса формирования компонент векторов р (f) и A(f) из вектора п (f)(0;1, 0,1, 1,0) устройством:


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления симметрических булевых функций | 1988 |
|
SU1559337A1 |
| Устройство для полиномиального разложения симметрических булевых функций | 1988 |
|
SU1559338A1 |
| Устройство для вычисления симметрических булевых функций | 1991 |
|
SU1833860A1 |
| Многофункциональный логический модуль | 1989 |
|
SU1676093A1 |
| Устройство для вычисления симметрических булевых функций | 1990 |
|
SU1748150A1 |
| Устройство для вычисления симметрических булевых функций | 1990 |
|
SU1742811A1 |
| Многофункциональный логический модуль | 1991 |
|
SU1793542A1 |
| Устройство для вычисления симметрических булевых функций | 1990 |
|
SU1789976A1 |
| Многофункциональный логический модуль | 1989 |
|
SU1598161A1 |
| Устройство для вычисления фундаментальных симметрических булевых функций | 1990 |
|
SU1789978A1 |
. Изобретение относится к вычислительной технике и предназначено для использования в ЭВМ и спецпроцессорах с системой команд высокого уровня, ориентированной на класс логико-комбинаторных задач. Цель изобретения - повышение быстродействия устройства для арифметического разложения симметрических булевых функций. Поставленная цель достигается тем, что устройство для арифметического разложения симметрических булевых функций п аргументов содержит п+1 группу вычитателей, вход константы логического нуля,- п+1 входов.. п+1 выходов первой группы и п+1 выходов второй группы. Устройство работает следующим образом. На входы устройства подаются компоненты двоичного кода л (f) разлагаемой симметрической булевой функции (xi, X2Хп). На выходах первой группы формируются компоненты вектора р (f), являющиеся коэффициентами положительного поляризованного арифметического полинома G(f) функции f, а на выходах второй группы - компоненты векторов A (f), являющиеся коэффициентами отрицательно поляризованного арифметического полинома H(f). 1 ил.
Выход аыч. 6 г 111110
Выход
БЫЧ.11
О, 000100
Выход выч.7 000010
Выход выч . 8 111111
Выход выч.12 111101
Вы вы 00
ВыходВыход
выч.15выч.16
000. 000000 9
Отсюда
Выход выч.17 ps 001010
Выход
выч.18
110110 fl s
р0 0000002 0,а; р, 0000012
Рг -СМ 111 °21доп -2 о ; р. 0001
pi tni°0 2 Aon -7 o ; Ps оою
Й0 000000г ; 4 00000.1 в
Си111Удоп -1о,о; Ь ооо
4 000011г 5 Dl°110Формула изобретения Устройство для арифметического разлог жения симметрических булевых функций, содержащее вычитатели, отличающее- с я тем, что, с целью повышения быстродействия, вычитатели образуют п+1 группу (п - количество аргументов разлагаемой симметрической булевой функции), (2г-1)-я и 2г-я (,2;... п/2) из которых содержат по п -2(г-1) вычитателей. первый вход устройства соединен с входом вычитаемого первого вычитателя первой группы и первым выходом первой группы выходов устройства, 1-й вход устройства (. 3 п)
соединен с входом вычитаемого 1-го вычитателя первой труппы и входом уменьшаемого (Ы)-го вычитателя первой группы, (п+1)-й вход устройства соединен с входом уменьшаемого n-го вычитателя первой группы и первым выходом второй группы выходов устройства, выход первого вычитателя (М)-й группы соединен с i-м выходом
Выход выч.10 000001 Ц
Выход выч.13 000000
«, ;
2
о;
ог
o(T
0
5
0
5
4-«;
10,о; .
Ю10 .
первой группы выходов устройства и входом вычитаемого первого вычитателя 1-й группы, выход первого вычитателя n-й группы соединен с (п+1)-м выходом первой группы выходов устройства, выход k-ro
вычитателя р-й группы (, 3 n-р; ,
2,..., п-2) соединен с входом уменьшаемого k-ro вычитателя (р+1)-й группы и входом вычитаемого (k-l)-ro вычитателя (р+1)-й группы, выход (n-i+2)-ro вычитателя (И)-й группы соединен с входом уменьшаемого (п-1+1)-го вычитателя i-й группы, вход вычитаемого п-2(г-1)-го вычитателя 2г-й группы соединен с выходом п-2(г-1)-го вычитателя (2г-1)-й группы, вход уменьшаемого п-2(г-1)-го вычитателя 2г-й группы соединен с входом константы логического нуля, а выход - с (г+1)-м выходом второй группы выходов устройства, ()-й выход второй группы выходов устройства соединен с выходом (n-2l+1 hro вычитателя 21-й группы (, 2..., Xn-1)/2Q.
26-19
231 U 
| Устройство для арифметического разложения логических функций | 1989 |
|
SU1633388A1 |
| кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Кухарев Г.А., Тропченко А.Ю., Шмер- ко В.П | |||
| Систолические процессоры для обработки сигналов | |||
| - Минск: Белоруссия, 1988, с | |||
| Приспособление для записи звуковых явлений на светочувствительной поверхности | 1919 |
|
SU101A1 |
| рис | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
Авторы
Даты
1992-02-07—Публикация
1989-04-11—Подача