Изобретение относится к технике ультразвуковой вычислительной томографии и может быть использовано для организации томографического исследования различных физических и
биологических объектов в медицине, биологии, гидро- и геофизике и дефектоскопии,
Цель изобретения - повышение точности эффективности реконструкции за счет
упрощения процесса сбора данных и оптимизации процедуры обработки и возможности реконструкции высококонтрастных неоднородностей, когда необходим учет процесса многократного перерассеяния ультразвуковой волны на неоднородности.
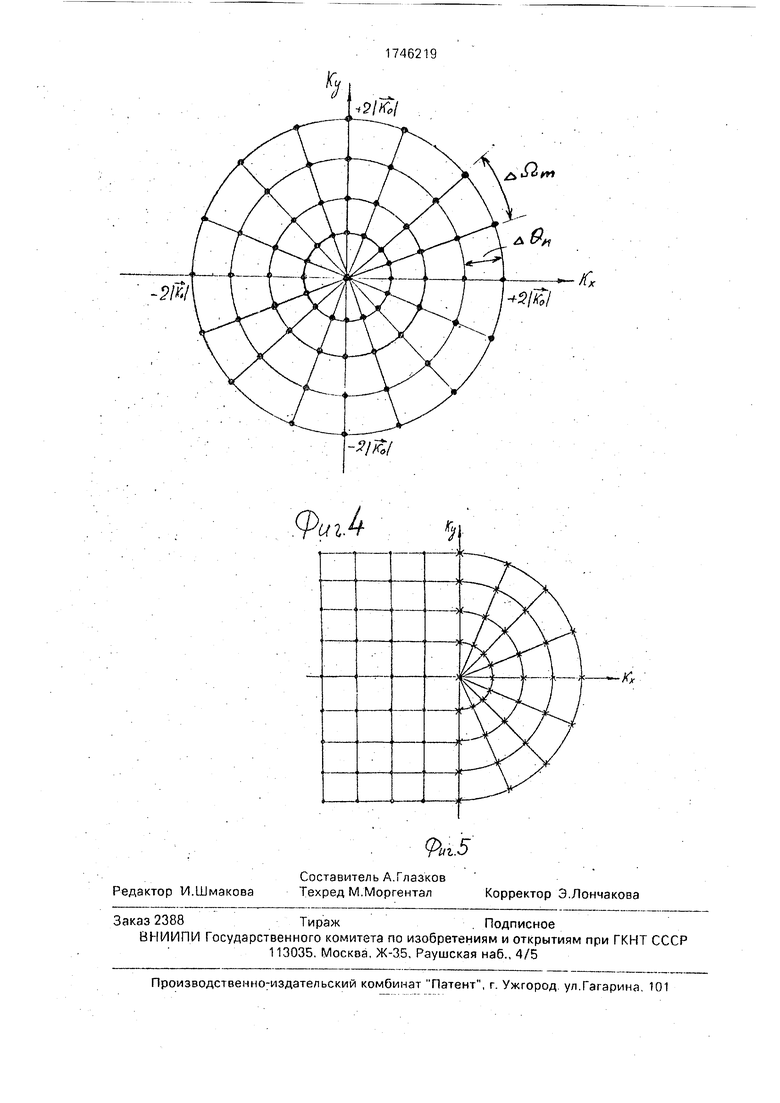
На фиг. 1 приведена схема организации томографического исследования; на фиг. 2 - векторная диаграмма в спектральном фурье-пространстве; на фиг. 3 - выборка дискретных компонентов пространственного спектра неоднородности при фиксированном значении Оп и пробегании On всех своих значений; на фиг. 4 -- полная структу- .ра данных о пространственном спектре исследуемой неоднородности, получаемая при пробегании углами вп и Цп всех своих значений (полностью совпадает с типичными структурами данных, получаемых для случая лучевой вычислительной томографии); на фиг 5 -- координатные сетки в пря- моугольной декартовой и полярной системах координат (крестиками обозначены узлы полярной сетки, в которых измерены значения пространственного спектра неоднородности; черными кружками - узлы декартовой сетки).
На фиг. 1-5обозначенывп дискретный угол перемещения протяженного линейного преобразователя, исполняющего роль приемника ультразвука, по окружности С вокруг исследуемого объекта R, On - дискретный угол поворота исследуемого объекта вокруг некоторой внутренней точки, являющейся началом полярной системы координат; Ко - волновой вектор падающей акустической волны; Кп - волновой вектор плоской акустической волны, рассеянной под углом On, причем |КПЫ Ко : -Пит - вектор, для которого на томографической установке при фиксированных углах 6п и On измеряется значение пространственного спектра исследуемой неоднородности
(Лит Кп Ко).
Способ томографической реконструкции акустических неоднородностей заключается в следующем.
Исследуемый объект, описываемый функцией Ј(г) и локализованный в области R (фиг. 1), помещают в имерсионную жидкость и облучают плоской ультразвуковой волной. На приемной апертуре С. представляющей собой окружность с центром в начале полярной системы координат, помещенным в области R, регистрируют плоские ультразвуковые волны частоты К0Со, где и)0 частота исходной плоской волны. Ко - волновое число; Со - скорость звука в имерсионной жидкости. При этом приемные преобразо0
5
0
5
0
5
0
5
O
5
ватели располагаются в дальней волновой зоне относительно рассеивающего объекта. Разложение рассеянного акустического поля на плоские ультразвуковые волны и регистрация последних достигается тем, что в качестве приемников ультразвука используют протяженный линейный преобразователь, длина которого значительно превышает длину волны Я зондирующего излучения. Такой преобразователь в силу усреднения значений акустического поля по всей своей поверхности выделяет из него плоскую волну, распространяющуюся в направлении нормали к поверхности преобразователя, и формирует электрический сигнал, связанный с амплитудой и фазой этой плоской волны.
Приемные акустические преобразователи могут располагаться на окружности С в
г -.
точках с угловыми координатами Оп -гг- п,
где вп - величина угла, образованного волновыми векторами К0 (падающей волны) и Кп (плоской волны, рассеянной под углом вп). или можно использовать один приемный преобразователь, который может перемещаться по С на дискретные углы вп; причем N - общее количество дискретных положений приемных преобразователей (или преобразователя).
В ряде случаев удобно иметь несколько приемных преобразователей на С и одновременно использовать возможность их дискретного перемещения. Целесообразность такого сочетания определяется соотчоше- нием между размерами преобразователя и радиусом окружности С. Использование подобной схемы позволяет увеличить скорость съема экспериментальных данных.
Таким образом достигается разложение рассеянного поля по плоским акустическим волнам, рассеянным под различными углами вп.
Для каждого фиксированного 9п осуществляется полный поворот объекта вокруг начала полярной системы координат посредством дискретных шагов Qn. При этом
Ол -тт- гп, где М - общее количество дискретных положений объекта при повороте.
В случае рассеивателя Ј(г) борновского типа пространственный спектр рассеивате- ля Ј(Л) с точностью до постоянного множи- тепя равен отношению комплексной амплитуды гтлоской волны, рассеянной в направлении К, к комплексной амплитуде плоской волны, падающей на объект в направлении R0 (Л К- К0).
Данной методике съема томографических данных (а измеряется амплитуда и фаза плоских рассеянных волн) в этом случае соответствует выборке компонент пространственного спектра объекта Ј(Л), где Л (Кх - Кох, К0у - Коу) в диапазоне Л I 2К0 в пространстве волновых векторов (Кх, Ку).
Для фиксированного угла вп направление падающего поля совпадает с положительным направлением оси ОХ. Векторная диаграмма волновых векторов для данного случая представлена на фиг. 2, Разностный вектор Лпт образует с осью ОКХ в пространстве волновых векторов угол От, соответствующий m-му углу поворота объекта.
Совершение полного оборота объекта вокруг начала полярной системы координат в реальном пространстве при рассмотрении борновского приближения теории дифракционного рассеивания сопровождается образованием выборки дискретных компонент пространственного спектра в пространстве волновых векторов на окружности раДИуСЭ; Лum| {фИГ. 3)
Повторяя процедуру съема данных для каждого фиксированного угла вп, получают структуру данных о пространственном спектре исследуемого объекта в пространстве волновых векторов, представленную на фиг. 4. При этом дискретизация по углу Оп соответствует дискретизации по радиусу в пространстве волновых векторов а дискретизация по углу поворота объекта От соответствует дискретизации спектральных данных по углу в фурье-пространстве.
Таким образом, получают в пространстве волновых векторов выборки данных о пространственном спектре объекта по концентрическим окружностям различных радиусов с общим центром в начале координат. Полученная структура данных о пространственном спектре исследуемой неоднородности полностью совпадает с типичной структурой спектральных данных в лучевой вычислительной томографии, где применяются стандартные алгоритмы восстановления изображения неоднородности на основе структуры спектральных данных, соответствующей размещению данных на прямых, проходящих через начало координат.
Эти вычислительные алгоритмы основаны на процедуре интерполяции данных с круговых сеток в узлы эквидистантной прямоугольной сетки в пространстве волновых векторов, которая требуется для выполнения обратного фурье-преобразования методом БПФ (быстрого преобразования Фурье).
На фиг. 5 показано расположение точек (п AL, mAQ) в плоскости волновых векторов, в которых определяются значения фурье- образа функции Ј. Эти точки, образующие 5 полярную систему, обозначены крестиками ( Д1 - дискретизация этой полярной системы по радиусам, Д Q- по углам). Кружками на фиг. 5 обозначены отсчеты (т1 ДКХ, п1 ДКУ), в которых необходимо знать значения спек0 тра объекта для его восстановления ( АКХ и ЛКу) - дискретизация в прямоугольной системе координат),
Полученная структура ультразвуковых томографических данных о пространствен5 ном спектре исследуемого объекта, учитывающих процесс дифракции на объекте акустических волн, допускает полную адаптацию существующих хорошо разработанных алгоритмов обработки томографи0 ческих данных, используемых в рентгеновской вычислительной томографии (где не учитываются явления дифракции зондирующего излучения).
Восстановление изображения исследу5 емого объекта производится путем однократного двухкоординатного обратного фурье-преобразования функции Ј (Л) на декартовой прямоугольной сетке в пространстве волновых векторов в функцию Ј (PJ в
0 реальном пространстве.
Таким образом, предложенный способ дифракционного томографического исследования акустических объектов отличается от известных технических решений методом
5 получения данных акустического рассеяния . непосредственно в виде значений пространственного спектра исследуемой нео- днородости на полярной сетке в фурье-пространстве, что достигается изме0 рением в ходе исследования амплитуды и фазы рассеянных плоских волн, на которые производится физическое разложение рассеянного звукового поля с помощью протяженных линейных приемных преобразо5 вателей. Получаемая таким образом на по- .лярной сетке в фурье-пространстве структура спектральных данных позволяет для дальнейшего восстановления изображения неоднородности использовать стандарт0 ные, хорошо разработанные алгоритмы лучевой вычислительной томографии. Разложение рассеянного акустического поля по плоским волнам позволяет также эффективно учитывать процесс многократного
5 перерассеяния зондирующей волны на неоднородности, что необходимо для получения возможности восстановления высококонтрастных(неборновских) неодно- родностей.
Данный способ удобен для реализации в практических устройствам позволяет использовать хорошо разработанные стандартные алгоритмы и программное обеспечение рентгеновской вычислительной томографии и, следовательно, может найти широкое применение
Формула изобретения Способ томографической реконструкции акустических неоднородностей, заключающийся в облучении исследуемого обьекта плоской ультразвуковой волной с фиксированного направления с возможностью поворота объекта вокруг некоторой внутренней точки, являющейся одновре менно центром поворота приемной акустической системы, измерении амплитуды и фазы рассеянного ультразвукового поля, учете дифракционных эффектов и обработ:-
ке получаемых данных в фурье-пространст- ве с помощью ЭВМ, отличающийся тем, что, с целью повышения точности и эффективности реконструкции за счетупро5 щения процесса сбора данных и оптимизации процедуры обработки и возможности реконструкции высококонтрастных неоднородностей, разлагают рассеянное ультразвуковое поле на плоские акустические
10 волны с помощью приемной акустической системы, состоящей, как минимум, из одного протяженного линейного преобразователя измеряют амплитуду и фазу этих волн, организуют на основе результатов изме- 15 рений, структуру исходных данных для обработки на радиально-круговой сетке в фурье-пространстве, а обработку ведут с помощью стандартных алгоритмов лучевой вычислительной томографии
20



| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ВОССТАНОВЛЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВОЛНОВЫХ НЕОДНОРОДНОСТЕЙ СРЕДЫ, МЕНЯЮЩИХСЯ ВО ВРЕМЕНИ | 1995 |
|
RU2099690C1 |
| СПОСОБ ФОРМИРОВАНИЯ ТОМОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ | 2005 |
|
RU2312602C2 |
| УЛЬТРАЗВУКОВОЙ ТОМОГРАФ | 2012 |
|
RU2530659C2 |
| Способ микроволновой томографии сверхвысокого разрешения | 2017 |
|
RU2662079C1 |
| Способ определения акустической плотности | 2017 |
|
RU2657314C1 |
| УСТРОЙСТВО УЛЬТРАЗВУКОВОЙ ИНТРОСКОПИИ | 2008 |
|
RU2359265C1 |
| УЛЬТРАЗВУКОВОЙ ТОМОГРАФ | 2012 |
|
RU2526424C2 |
| УЛЬТРАЗВУКОВАЯ АНТЕННАЯ РЕШЕТКА | 2007 |
|
RU2335038C1 |
| УЛЬТРАЗВУКОВОЙ ТОМОГРАФ И КОЛЬЦЕВАЯ АНТЕННАЯ РЕШЕТКА ДЛЯ УЛЬТРАЗВУКОВОГО ТОМОГРАФА | 1999 |
|
RU2145797C1 |
| СПОСОБ ИЗМЕРЕНИЯ РАСПРЕДЕЛЕНИЯ ВЕКТОРНОЙ ФУНКЦИИ МАГНИТНОЙ ИНДУКЦИИ ПЕРИОДИЧЕСКОГО МАГНИТНОГО ПОЛЯ | 2011 |
|
RU2463620C1 |


Изобретение относится к технике ультразвуковой вычислительной томографии. Целью изобретения является повышение точности и эффективности реконструкции за счет упрощения процесса сбора данных и оптимизации процедуры обработки и возможности реконструкции.высококонтрастных неоднородностей. Облучают плоской ультразвуковой (у.з.) волной объект с возможностью его поворота вокруг точки, являющейся центром поворота приемной акустической системы, состоящей из протяженных линейных преобразователей, осуществляя таким образом физическое- разложение рассеянного у.з. поля на плоские акустические волны, измеряют их амплитуду и фазу и обрабатывают полученные данные в фурье-пространстве с помощью ЭВМ. Разложение у.з. поля с помощью протяженных линейных преобразователей позволяет получить данные акустического рассеяния непосредственно в виде значений пространственного спектра неоднородностей на полярной сетке в фурье-пространстве, что обеспечивает возможность использовать для дальнейшей обработки данных хорошо разработанные стандартные алгоритмы лучевой вычислительной томографии и реализовать упрощение сбора данных и оптимизацию обработки. В то же время процедура обработки, организованная на основе указанного разложения, учитывает порцесс многократного пере- рассения зондирующей волны, что дает возможность реконструировать высококонтрастные неоднородности. 5 ил. (Л С VI Jbb О ю о
Задающая плоская
80S1HGF
Яротяженньш линейный ярео&риэобатель
Фиг.1
Щ-f,. m
Ъ-Ъ-W
&
6129 W. I
| Wolf E | |||
| Three - dimensional structure determination of semi - transparent object from holographic data | |||
| - Opt.Commun | |||
| Приспособление к индикатору для определения момента вспышки в двигателях | 1925 |
|
SU1969A1 |
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| Гринлиф Дж.Ф | |||
| Ультразвуковая реконструктивная томография | |||
| - ПТИИЭР, 1983, т.71, №3, с.54-63 | |||
| Davaney A.I | |||
| A filtred backprogation algarithm for diffraction tomography | |||
| - Ultrasonic Imaging, 1983 | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| 336-349 | |||
| Kaveh M | |||
| et al | |||
| Ultrasonic tomography based on perturbation solutions of the wave equation | |||
| Computed Graphics and Image Processing, 1979, №9, p.105-116 | |||
| Вайнберг Э.И., Файнгойз М.Л, Оптимальная дискретизация и интерполяция проекций в рентгеновской вычислительной томографии | |||
| - Дефектоскопия, 1984, № 8, с.49-59. | |||
Авторы
Даты
1992-07-07—Публикация
1989-05-16—Подача