Изобретение относится к информационно-измерительной технике, в частности к магнитометрии, и может быть использовано для получения и визуализации распределенных в пространстве и периодически изменяющихся во времени магнитных полей внутри тела с неоднородными магнитными свойствами без механического проникновения в него.
Известен способ топографии магнитного поля, реализованный в устройстве [1], который основан на измерении магнитного поля одновременно в большом количестве точек плоскости посредством матричной регулярной структуры из столбцов и строк взаимосвязанных элементов, расположенных на полупроводниковой пластине. Однако известные способ и устройство для его реализации не позволяют выполнять измерения в каждой точке исследуемого объема, при наличии в нем тела без механического проникновения внутрь него, а позволяют получить только одну составляющую вектора магнитной индукции, одинаково направленную с нормалью к полупроводниковой пластине. Кроме того, способ имеет ограничения по количеству согласованных точечных датчиков (элементов).
Известен способ сканирования магнитного поля, реализованный в устройстве [2], который основан на измерении магнитного поля поочередно в количестве точек плоскости посредством последовательно соединенной матрицы чувствительных элементов, включающей N феррозондов, с последующей обработкой измеряемых напряжений с помощью ЭВМ. Однако известные способ и устройство для его реализации не позволяют выполнять измерения в каждой точке исследуемого объема, при наличии в нем тела без механического проникновения внутрь него, а позволяют получить только одну (из трех) составляющую вектора магнитной индукции. Кроме того, способ имеет ограничения по количеству феррозондов и, как следствие, по разрешающей способности.
Известен способ для измерения и топографии магнитных полей рассеяния вблизи поверхности объекта, реализованный в устройстве [3], который основан на последовательном перемещении в соответствии с заданной траекторией с помощью измерительной штанги одного трехкомпонентного датчика Холла относительно объекта измерения посредством блока механических перемещений с поворотным столиком и подвижными каретками, приводимыми в движение шаговыми двигателями, с последующей статистической обработкой результатов измерения измерительно-вычислительным блоком. Однако известные способ и устройство для его осуществления не позволяют выполнять измерения в каждой точке исследуемого объема, при наличии в нем тела без механического проникновения внутрь него, а требуют многократных измерений в каждой точке и поэтому трудоемки и продолжительны во времени. Кроме того, используемый статистический подход не позволяет получать распределений, характеризующих мгновенное состояние переменного магнитного поля.
Наиболее близким к заявляемому является способ получения распределения векторной функции магнитной индукции периодического магнитного поля [4], реализованный в устройстве [5], основанный на последовательных поступательных и угловых перемещениях магниточувствительного рабочего органа, при этом исследуемый объем представляют совокупностью параллельных сечений, распределения магнитной индукции в которых получают посредством применения процедуры реконструкции вычислительной томографии к напряжениям, индуцируемым в соответствии с законом Фарадея в контурах, перемещающихся в магнитном поле, а результирующее распределение в пространстве для каждой из трех компонент векторной функции магнитной индукции представляют в виде квадратной матрицы из n строк и n столбцов, каждый элемент которой является значением составляющей вектора магнитной индукции, усредненной в пределах элементарной площадки, в результате чего для каждого j-го измерения магнитный поток, пронизывающий контур, является суммой потоков, располагающихся вдоль контура элементарных площадок с соответствующими значениями индукции. Однако известные способ и устройство для его осуществления не позволяют выполнять измерения в каждой точке исследуемого объема, при наличии в нем тела с неоднородными магнитными свойствами тела без механического проникновения внутрь него.
Техническим результатом применения заявляемого способа является расширение функциональных возможностей магнитометрии, заключающееся в измерениях распределения векторной функции магнитной индукции периодически изменяющего во времени поля в любых точках исследуемого пространства для произвольно выбранных моментов времени на периоде и основанное на последовательных поступательных и угловых перемещениях рабочего магнитоизмерительного органа, выполненного в виде ортогонально ориентированных в пространстве контуров, а также на представлении исследуемого объема совокупностью параллельных сечений, распределения магнитной индукции в которых получают посредством применения процедуры вычислительной томографии к индуцируемым напряжениям, посредством использования рабочего органа определенной формы и метода вычислительной томографии, доработанного под способ измерения.
Технический результат, реализуемый в способе измерения распределения векторной функции магнитной индукции периодического магнитного поля, достигается тем, что измерения осуществляют без механического проникновения внутрь тела, расположенного в исследуемом пространстве, а рабочий магнитоизмерительный орган реализуют на основе двух одинаковых пар контуров в виде катушек индуктивности с равным числом витков и встречным включением обмоток в каждой паре, привязанных к декартовой системе координат рабочего органа, причем первый контур пары имеет по центру выполненный под прямыми углами характерный двойной изгиб в виде ступени, которым образованы три поверхности, пронизываемые магнитным потоком, а второй контур пары - плоский и имеет одну поверхность, в свою очередь каждые из четырех образованных поверхностей контуров пар имеют такое взаимное расположение, при котором вектор нормали плоского контура коллинеарен двум векторам изогнутого контура и перпендикулярен его третьей нормали, выставленной к ступени, причем, если процесс измерения в присутствии тела выполняют при локальной однородности магнитного поля, выраженной наличием на произвольно выбранном интервале, равном половине ширины ступени, постоянства значений проекций векторной функции на нормаль к поверхности контуров, тогда при совмещении плоского и изогнутого контуров пары с некоторой погрешностью считают, что магнитный поток, пронизывающий поверхности изогнутого контура, будет компенсироваться магнитным потоком встречно включенного плоского контура за исключением магнитного потока, пронизывающего плоскость ступени, а сканирование позволяет получить необходимые для алгоритма реконструкции метода вычислительной томографии исходные проекционные данные всех трех компонент векторной функции магнитной индукции в сечении:
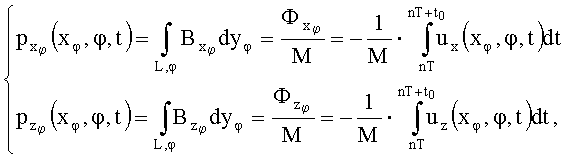
где 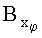 и
и  - компоненты векторной функции индукции в системе координат рабочего органа (хφ,уφ,zφ); uх и uz - напряжения, индуцируемые изменением магнитного потока
- компоненты векторной функции индукции в системе координат рабочего органа (хφ,уφ,zφ); uх и uz - напряжения, индуцируемые изменением магнитного потока 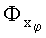 и
и 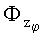 в парах контуров;
в парах контуров; 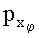 и
и  - значения линейных проекций лучевых сумм функции индукции
- значения линейных проекций лучевых сумм функции индукции 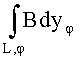 на ось хφ; φ - угол между системами координат рабочего органа и тела; L - траектория интегрирования, совпадающая с длинной ступени; М - ширина ступени; n=1, 2, … - номер периода; t - время; Т- период, в течение которого происходит одно полное изменение векторной функции магнитной индукции; t0 - текущее значение времени на периоде, причем в системе координат (x,y,z) неподвижного тела через формулы поворота, с учетом
на ось хφ; φ - угол между системами координат рабочего органа и тела; L - траектория интегрирования, совпадающая с длинной ступени; М - ширина ступени; n=1, 2, … - номер периода; t - время; Т- период, в течение которого происходит одно полное изменение векторной функции магнитной индукции; t0 - текущее значение времени на периоде, причем в системе координат (x,y,z) неподвижного тела через формулы поворота, с учетом 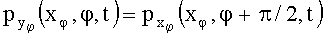 и совпадения осей zφ=z:
и совпадения осей zφ=z:
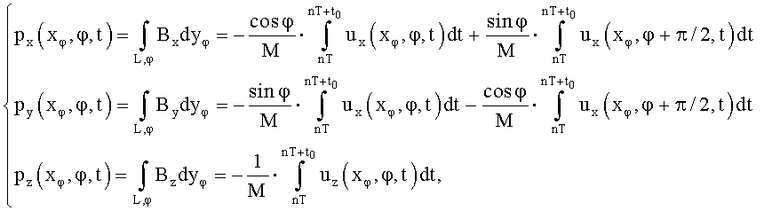
при этом двумерное распределение векторной функции магнитной индукции в сечении получают из трех ее компонент посредством применения к исходным проекционным данным px, py, pz, алгоритма реконструкции, реализованного путем свертки проекционных данных, осуществляющей фильтрацию с использованием свертывающей функции h(xφ), являющейся обратным Фурье-преобразованием частоты пространственного спектра по формуле:
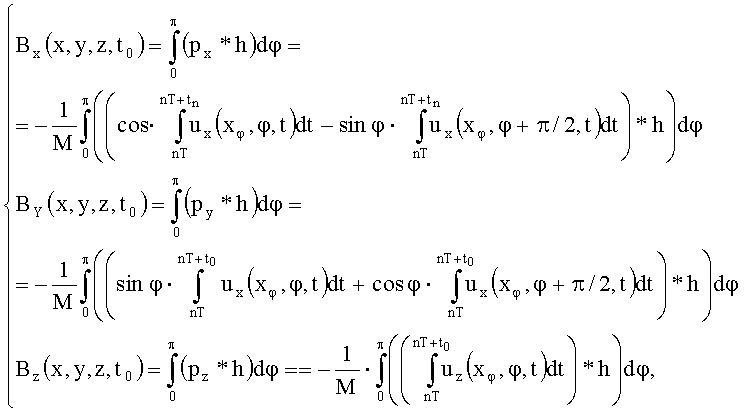
где символ «*» есть оператор свертки; Bx(x,y,z,t0), By(x,y,z,t0), Bz(x,y,z,t0)-х-, у-, z-компоненты векторной функции магнитной индукции 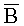 , соответственно, а затем соединяют отдельные двумерных распределений векторной функции индукции в сечениях в общую картину трехмерного распределения в пространстве.
, соответственно, а затем соединяют отдельные двумерных распределений векторной функции индукции в сечениях в общую картину трехмерного распределения в пространстве.
Суть способа измерения векторной функции магнитной индукции периодического магнитного поля заключается в неразрушающих тело с неоднородными магнитными свойствами измерениях векторной функции магнитной индукции периодического во времени магнитного поля в любых точках исследуемого пространства для произвольно выбранных моментов времени без механического проникновения внутрь тела и достигается тем, что рабочий магнитоизмерительный орган реализуется в виде двух одинаковых ортогонально ориентированных относительно друг друга пар контуров, выполненных в виде катушек индуктивности с равным числом витков и встречным включением обмоток в каждой паре, привязанных к декартовой системе координат рабочего органа (xφ,уφ,zφ). Первый контур пары имеет по центру выполненный под прямыми углами характерный двойной изгиб, напоминающий узкую ступень, которым образованы три поверхности, пронизываемые магнитным потоком. Второй контур пары - плоский и имеет одну поверхность. Каждая из четырех образованных поверхностей контуров пары имеет свои геометрические размеры и описывается соответствующим вектором нормали, умноженным на скаляр значения площади поверхности. В паре контуры имеют такое взаимное расположение, при котором плоский контур находится посередине ширины изгиба изогнутого контура, так что вектор нормали плоского контура коллинеарен двум векторам изогнутого контура и перпендикулярен его третьей нормали, выставленной к ступени. Если в процессе измерения в присутствии тела с неоднородными магнитными свойствами выполняется обязательное требование локальной однородности магнитного поля, выраженной наличием на произвольном выбранном интервале, равном половине ширины ступени М (фиг.1,а), постоянства значений проекции векторной функции на ось, ортогональную плоскостям S1', S1'' и S2', S2'', тогда при совмещении плоского и изогнутого контуров пары с некоторой погрешностью считается, что в каждой паре магнитный поток, пронизывающий поверхности изогнутого контура, будет компенсироваться магнитным потоком встречно включенного плоского контура за исключением магнитного потока, пронизывающего плоскость ступени Sx, Sz (фиг.1, 6).
Вследствие этого скалярное значение магнитного потока Ф вектора магнитной индукции 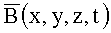 через поверхность S, образованную плоскостью узкой ступени, как вытекает из определения, есть поверхностей интеграл:
через поверхность S, образованную плоскостью узкой ступени, как вытекает из определения, есть поверхностей интеграл:
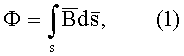
где S=M·L, причем М - ширина, a L - траектория интегрирования, совпадающая с длиной узкой ступени пар изогнутых контуров, соответственно (фиг.1,а).
Принимая во внимание, что дифференциал 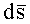 в выражении (1) для каждой пары соответственно равен:
в выражении (1) для каждой пары соответственно равен: 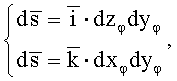 где
где 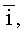
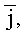
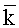 - орты системы координат (xφ,yφ,zφ), а площадь интегрирования в обоих случаях S, то поверхностный интеграл представляется двойным интегралом:
- орты системы координат (xφ,yφ,zφ), а площадь интегрирования в обоих случаях S, то поверхностный интеграл представляется двойным интегралом: 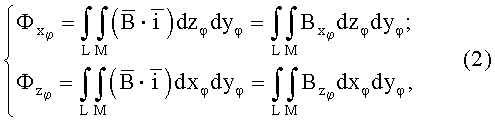
где 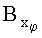 и
и  - компоненты
- компоненты 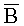 в системе координат рабочего органа.
в системе координат рабочего органа.
Принимая во внимание локальную однородность неоднородного в пространстве магнитного поля в пределах ширины узкой ступени М, интегрирование по осям хφ и zφ заменяется домножением на значение ширины М, а следовательно, выражение (2) приобретает следующий вид:
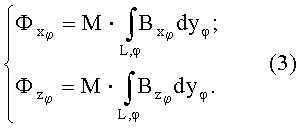
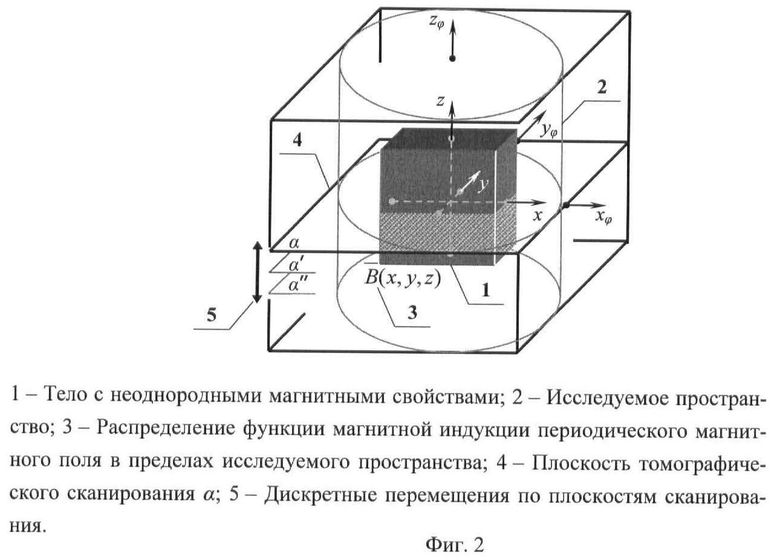
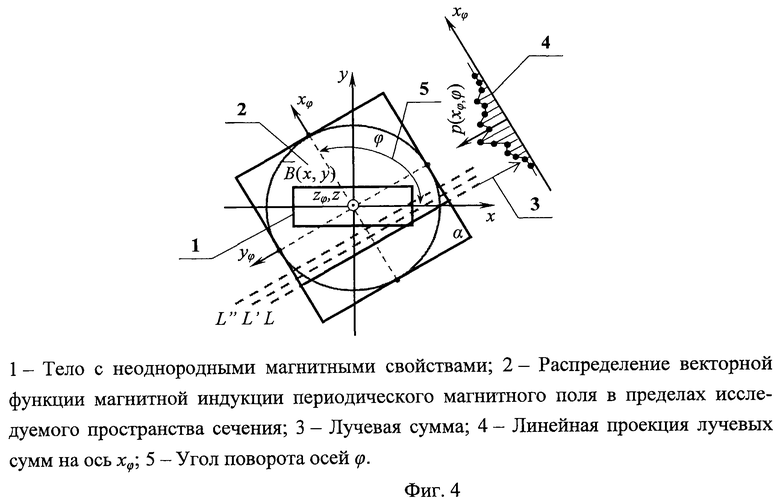
Процедура измерения начинается с того, что предварительно исследуемое трехмерное пространство с телом внутри условно разбивается на слои, образованные плоскостями α, α', α'', параллельными плоскости сканирования, что позволяет понизить размерность задачи до двумерной, представив данное пространство совокупностью дискретных сечений (фиг.2).
Последующее сканирование рабочим органом каждого отдельного сечения в соответствием с методом вычислительной томографии требует в отношении компонент векторной функции индукции измерения для многих пересекающихся под разными углами φ траекторий L значений р(хφ,φ) линейных проекций лучевых сумм функции индукции, 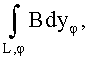 что с учетом (3) реализуется путем регистрации отнесенных к ширине ступени потоков магнитной индукции Ф:
что с учетом (3) реализуется путем регистрации отнесенных к ширине ступени потоков магнитной индукции Ф:
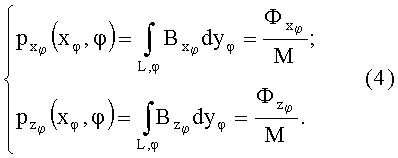
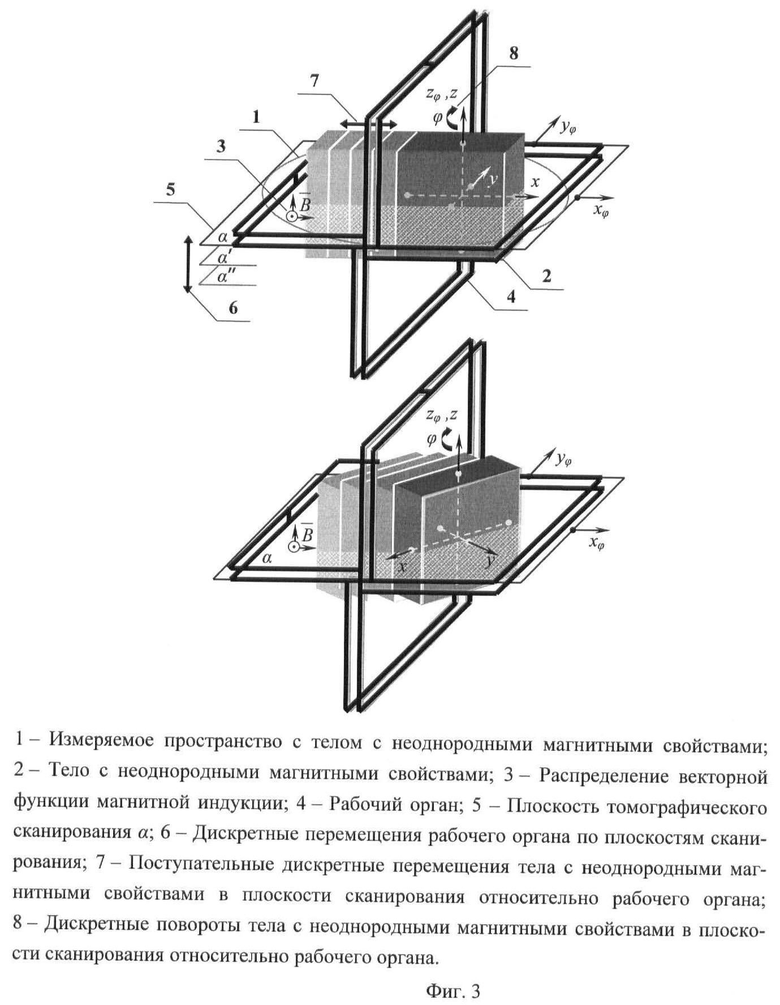
Таким образом, в ходе сканирования при перемещениях рабочего органа вдоль оси хφ и поворотах его относительно системы координат (х,у,z) тела на разные углы φ в интервале от 0 до π находится линейная проекция р(хφ,φ) лучевых сумм, выраженных интегралами вдоль прямой на интервале шириной L, численно равных магнитному потоку, отнесенному к ширине узкой ступени (фиг.3).
Согласно закону Фарадея напряжение u(t), наводимое в паре контуров, определяется выражением:
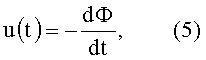
где dФ - дифференциал потока векторной функции индукции; dt - дифференциал времени.
Благодаря введенному условию периодичности во времени, согласно которому поле точно повторяет свои мгновенные состояния через одинаковые промежутки времени, равные периоду, продолжительность регистрации одной картины распределения поля уже не ограничена по времени длительностью интервала дискретизации, потому что регистрировать картину можно, осуществляя измерения в пространстве через интервалы времени, кратные периоду. И несмотря на то, что измерения значительно разнесены по времени, все они будут производиться для какого-то одного мгновенного состояния на периоде.
Выражая дифференциал dФ из уравнения (5) и интегрируя по времени t левую и правую части получившегося равенства, получают:
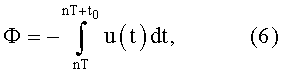
где Т - период, в течение которого происходит одно полное изменение изменения магнитной индукции; n=1, 2, … - номер периода; t0 - текущее значение времени на периоде.
Принимая во внимание уравнение (4) и (6), линейная проекция лучевых сумм функции индукции p(xφ,φ,t), теперь зависящая и от времени, записывается посредством отнесенных к ширине ступени интегралов по времени напряжений, индуцируемых изменением магнитного потока в соответствии с законом электромагнитной индукции Фарадея в парах контуров:
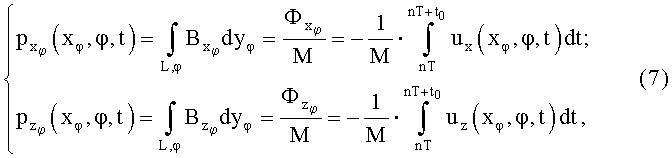
причем в системе координат (х,у,z) неподвижного тела через формулы поворота и с учетом 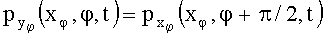 совпадения осей zφ=z получают:
совпадения осей zφ=z получают:
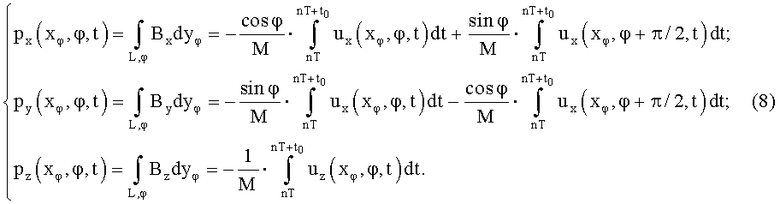
Данное обстоятельство позволяет получить необходимые для алгоритма реконструкции метода вычислительной томографии исходные проекционные данные всех трех компонент векторной функции магнитной индукции в сечении (фиг.4).
Двумерное распределение векторной функции магнитной индукции в сечении получают из трех ее компонент посредством применения алгоритма реконструкции к исходным проекционным данным, полученным в ходе сканирования.
Задача реконструкции изображения в вычислительной томографии сводится к решению основного интегрального уравнения (8) с нахождением распределения компонент Вх, Ву, Bz по измеренным значениям линейных проекций рх, ру, pz. Поэтому предлагаемый способ вынуждает воспользоваться алгоритмами реконструкции вычислительной томографии, базирующимися на аппарате преобразования Фурье, а именно обратной проекции с фильтрацией. Фильтрация осуществляется путем свертки проекций компонент непосредственно в пространстве оригинала Фурье-преобразования с соответствующей реализующей фильтрацию свертывающей функцией h(хφ), являющейся обратным Фурье-преобразованием частоты пространственного спектра [6]. Так из (8) получают:
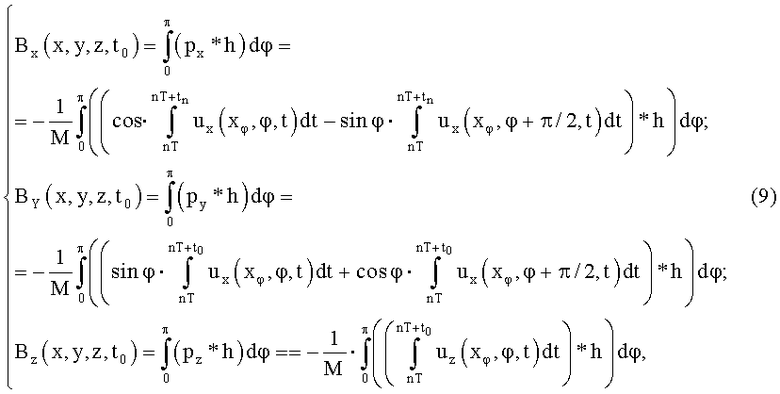
где символ «*» есть оператор свертки; Вх(х,у,z,t0), Ву(х,у,z,t0), Bz(х,у,z,t0)-х-, у-, z-компоненты векторной функции магнитной индукции  , соответственно.
, соответственно.
Процедура измерения заканчивается соединением отдельных двумерных распределений векторной функции индукции в сечениях в общую картину трехмерного распределения.
Таким образом, предложенный способ позволяет посредством использования метода вычислительной томографии получить трехмерное распределение векторной функции магнитной индукции периодического магнитного поля в любых точках исследуемого пространства и произвольно выбранных моментов во времени без механического проникновения внутрь тела с неоднородными магнитными свойствами, размещенного в исследуемом пространстве.
Литература
1. Авторское свидетельство СССР №1652951, кл. G01R 33/02, опубл. 30.05.1991.
2. Авторское свидетельство СССР №1762282, кл. G01R 33/02, опубл. 15.09.1992.
3. Авторское свидетельство СССР №1684761, кл. G01R 33/06, опубл. 15.10.1991.
4. Патент РФ №2179323, кл. G01R 33/02, опубл. 10.02.2002.
5. Патент РФ №2174235, кл. G01R 33/02, опубл. 27.09.2001.
6. Рентгенотехника. Справочник в 2-х книгах. Кн.2 / Под ред. В.В.Клюева. - М.: Машиностроение, 1988 г., с.319-326.
Предложен способ измерения распределения векторной функции магнитной индукции. В способе используется магнитоизмерительный орган в виде двух одинаковых ортогонально ориентированных относительно друг друга пар контуров, выполненных в виде катушек индуктивности с равным числом витков и встречным включением обмоток в каждой паре. Первый контур пары имеет по центру выполненный под прямыми углами характерный двойной изгиб в виде узкой ступени, которым образованы три поверхности, пронизываемые магнитным потоком, а второй контур пары - плоский и имеет одну поверхность. Исследуемое трехмерное пространство с телом внутри представляется совокупностью дискретных сечений. Техническим результатом является измерениях векторной функции магнитной индукции периодического во времени магнитного поля в любых точках исследуемого пространства для произвольно выбранных моментов времени без механического проникновения внутрь тела. 4 ил.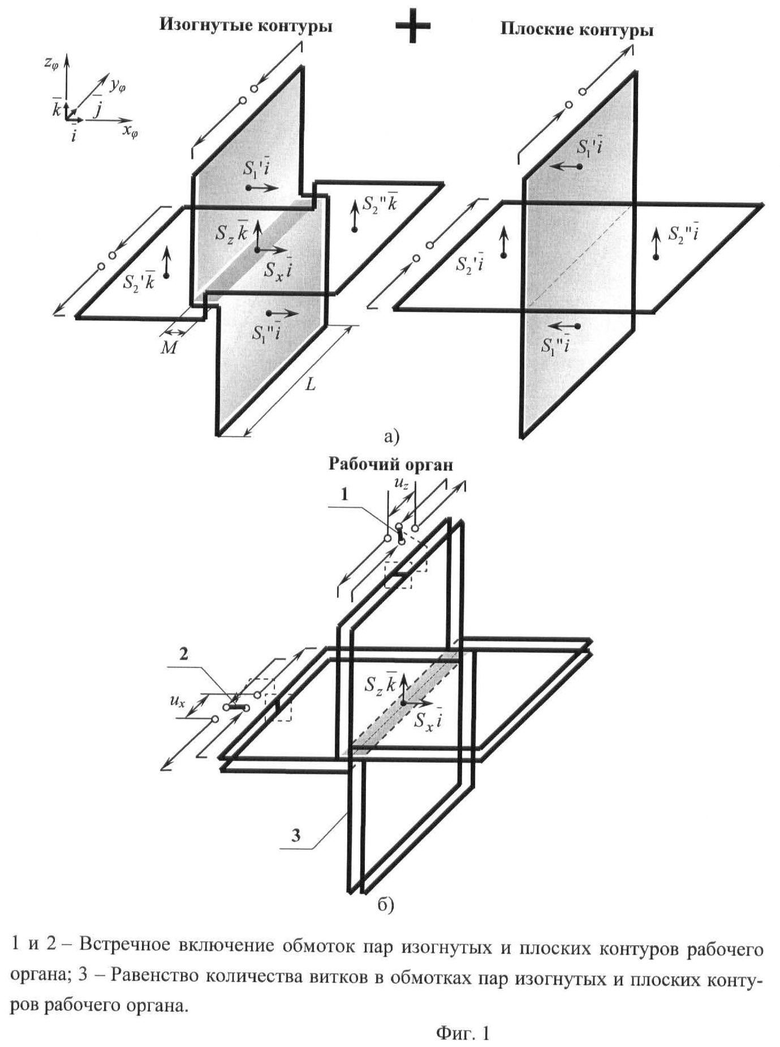
Способ измерения распределения векторной функции магнитной индукции периодического магнитного поля, заключающийся в измерениях распределения векторной функции магнитной индукции периодически изменяющего во времени поля в любых точках исследуемого пространства для произвольно выбранных моментов времени на периоде и основанный на последовательных поступательных и угловых перемещениях рабочего магнитоизмерительного органа, выполненного в виде ортогонально ориентированных в пространстве контуров, а также на представлении исследуемого объема совокупностью параллельных сечений, распределения магнитной индукции в которых получают посредством применения процедуры вычислительной томографии к индуцируемым напряжениям, отличающийся тем, что измерения осуществляют без механического проникновения внутрь тела, расположенного в исследуемом пространстве, а рабочий магнитоизмерительный орган реализуют на основе двух одинаковых пар контуров в виде катушек индуктивности с равным числом витков и встречным включением обмоток в каждой паре, привязанных к декартовой системе координат рабочего органа, причем первый контур пары имеет по центру выполненный под прямыми углами характерный двойной изгиб в виде ступени, которым образованы три поверхности, пронизываемые магнитным потоком, а второй контур пары - плоский и имеет одну поверхность, в свою очередь, каждые из четырех образованных поверхностей контуров пар имеет такое взаимное расположение, при котором вектор нормали плоского контура коллинеарен двум векторам изогнутого контура и перпендикулярен его третьей нормали, выставленной к ступени, причем, если процесс измерения в присутствии тела выполняют при локальной однородности магнитного поля, выраженной наличием на произвольно выбранном интервале, равном половине ширины ступени, постоянства значений проекций векторной функции на нормаль к поверхности контуров, тогда при совмещении плоского и изогнутого контуров пары с некоторой погрешностью считают, что магнитный поток, пронизывающий поверхности изогнутого контура, будет компенсироваться магнитным потоком встречно включенного плоского контура, за исключением магнитного потока, пронизывающего плоскость ступени, а сканирование позволяет получить необходимые для алгоритма реконструкции метода вычислительной томографии исходные проекционные данные всех трех компонент векторной функции магнитной индукции в сечении:
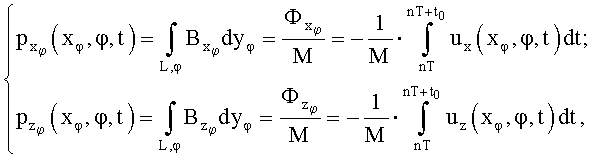
где 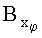 и
и  - компоненты векторной функции индукции в системе координат рабочего органа (xφ, yφ, zφ); ux и uz - напряжения, индуцируемые изменением магнитных потоков
- компоненты векторной функции индукции в системе координат рабочего органа (xφ, yφ, zφ); ux и uz - напряжения, индуцируемые изменением магнитных потоков 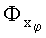 и
и 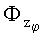 в парах контуров;
в парах контуров; 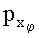 и
и  - значения линейных проекции лучевых сумм функции индукции
- значения линейных проекции лучевых сумм функции индукции 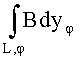 на ось хφ; φ - угол между системами координат рабочего органа и тела; L - траектория интегрирования, совпадающая с длиной ступени; М - ширина ступени; n=1, 2,… - номер периода; t - время; Т - период, в течение которого происходит одно полное изменение векторной функции магнитной индукции; t0 - текущее значение времени на периоде, причем в системе координат (х, y, z) неподвижного тела через формулы поворота, с учетом
на ось хφ; φ - угол между системами координат рабочего органа и тела; L - траектория интегрирования, совпадающая с длиной ступени; М - ширина ступени; n=1, 2,… - номер периода; t - время; Т - период, в течение которого происходит одно полное изменение векторной функции магнитной индукции; t0 - текущее значение времени на периоде, причем в системе координат (х, y, z) неподвижного тела через формулы поворота, с учетом 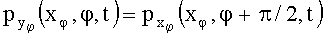 и совпадения осей zφ=z:
и совпадения осей zφ=z:
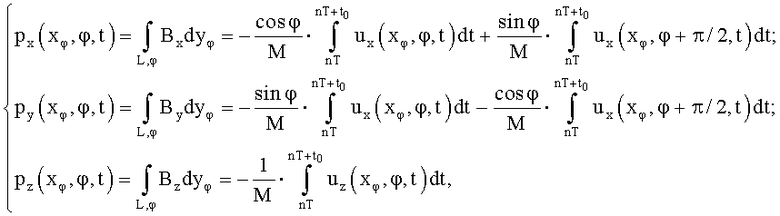
при этом двумерное распределение векторной функции магнитной индукции в сечении получают из трех ее компонент посредством применения к исходным проекционным данным рx, рy, pz, алгоритма реконструкции, реализованного путем свертки проекционных данных, осуществляющей фильтрацию с использованием свертывающей функции h(xφ), являющейся обратным Фурье-преобразованием частоты пространственного спектра по формуле
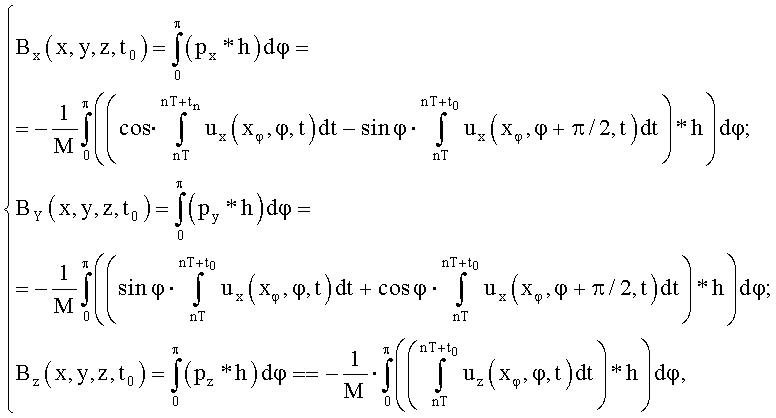
где символ «*» есть оператор свертки; Bx(x,y,z,t0), By(x,y,z,t0), Bz(x,y,z,t0) - х-, y-, z - компоненты векторной функции магнитной индукции 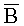 соответственно, а затем соединяют отдельные двумерных распределений векторной функции индукции в сечениях в общую картину трехмерного распределения в пространстве.
соответственно, а затем соединяют отдельные двумерных распределений векторной функции индукции в сечениях в общую картину трехмерного распределения в пространстве.
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ПЕРИОДИЧЕСКИХ МАГНИТНЫХ ПОЛЕЙ И ПОЛУЧЕНИЯ ИХ РАСПРЕДЕЛЕНИЙ В ПРОСТРАНСТВЕ И ВО ВРЕМЕНИ | 2000 |
|
RU2174235C1 |
| СПОСОБ ПОЛУЧЕНИЯ РАСПРЕДЕЛЕНИЯ ВЕКТОРНОЙ ФУНКЦИИ МАГНИТНОЙ ИНДУКЦИИ ПЕРИОДИЧЕСКОГО МАГНИТНОГО ПОЛЯ | 2000 |
|
RU2179323C1 |
| Устройство для сканирования магнитных полей | 1989 |
|
SU1762282A1 |
| JP 8068835 A, 12.03.1996. | |||
Авторы
Даты
2012-10-10—Публикация
2011-04-15—Подача