Изобретение относится к вычислительной технике, конкретно к устройствам декодирования кодов Рида-Маллера, и может быть использовано при разработке аппаратуры передачи дискретной информации.
Известно устройство декодирования кодов Рида-Маллера первого порядка длины 2П, содержащее буферный регистр, m блоков суммирования и вычитания, (т-1) блоков суммирования модулей, m блоков сравнения модулей, (т-1) блоков ключей и регистр записи декодированного слова.
Недостатком указанного устройства является меньшая по сравнению с декодированием по максимуму правдоподобия помехоустойчивость.
Известно устройство декодирования кодов Рида-Маллера первого порядка по максимуму правдоподобия, содержащее буферный регистр, (т-1) блоков суммирования и вычитчния блок попарного суммирования модулей, блок сравнения сумм пар модулей, блок ключей, блок суммирования и вычитания двух элементов, блок сравнения,
блок ключей т-го этапа, нуль-орган, регистр записи декодированного слова.
Недостатком данного устройства является высокая сложность реализации.
Целью изобретения является упрощение устройства.
Эта цель достигается тем, что в декодер кодов Рида-Маллера первого порядка по максимуму правдоподобия, содержащий последовательно соединенные входной буферный регистр, первый -{т-2)-й блоки сложения-вычитания, (2т - длина кода Рида-Маллера, m 1,2,..,), блок сравнения, выходы которого соединены с управляющими входами блока ключей, первые выходы которого подключены ко входам блока сложения-вычитания двух элементов, нуль-орган, выход которого соединен со входом (т+1)-го разряда выходного буферного регистра, входы входного и выходы выходного буферных регистров являются соответственно входами и выходами декодера, введе- ны первый - ()-й блоки вычисления коэффициентов корреляции и блок опредеVJVI
СЛ 00 СЛ
VI
ления номера максимального коэффициента корреляции, выходы ()-го блока сложения-вычитания подключены ко входам первого - ()-го блока вычисления коэффициентов корреляции, первые и вторые выходы которых соединены соответственно со входами блока сравнения и информационными входами блока ключей, выходы блока сложения-вычитания двух элементов и вторые выходы блока ключей соединены с первыми и вторыми входами блока определения номера максимального коэффициента корреляции, первый, второй и третий выходы которого подключены соответственно ко входу нуль-органа и входам первого и второго разрядов выходного буферного регистра, входы третьего - т-го разрядов которого подключены к выходам блока сравнения. Благодаря тому, что после (т-2)- го этапа вводится блок вычисления коэффициентов корреляции, достигается экономия аппаратурных затрат: требуемое число сумматоров уменьшается на -т х п 3 х 2т ,
кроме того в прототипе используются сумматоров,которые вычисляют сумму модулей входных величин. Такой сумматор является более сложным устройством, чем сумматор, вычисляющий просто сумму двух величин, так как операция взятия модуля требует определенных аппаратурных затрат. В предлагаемом устройстве количество сумматоров ищущих сумму модулей
пп
входных величин равно -j, т.е. на -т меньше,
чем в прототипе.
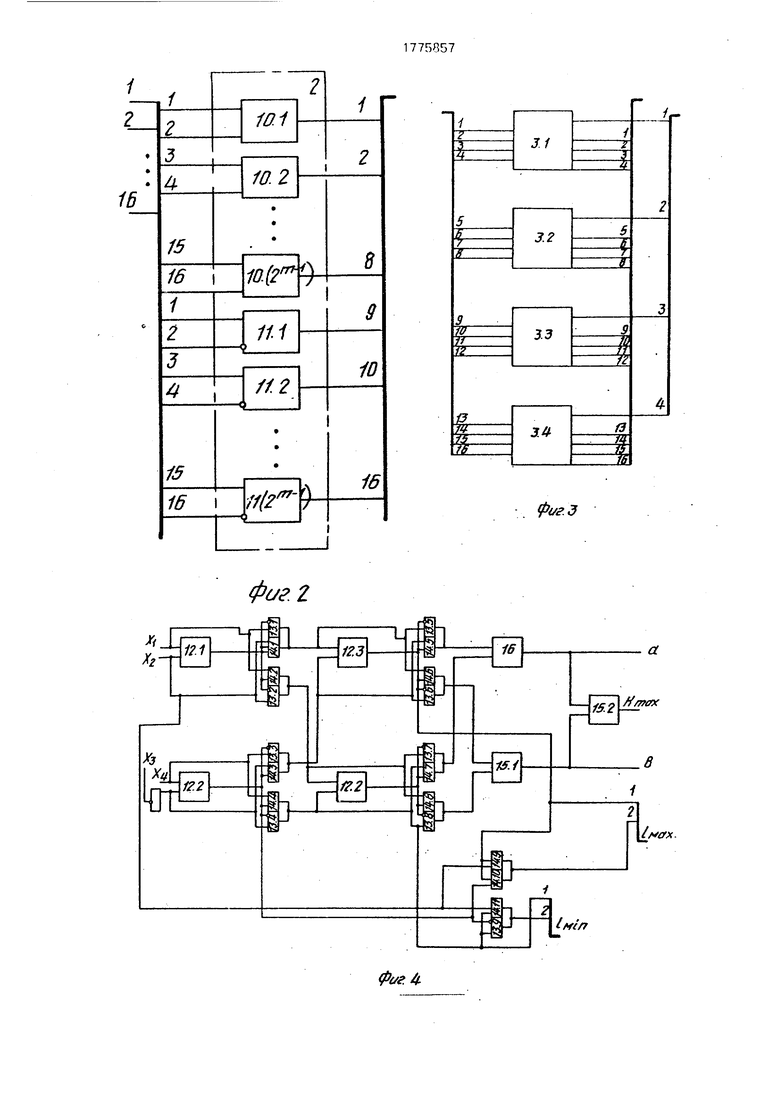
На фиг. 1 изображена структурная схема устройства декодирования. На фиг, 2 и 3 даны схемы подключения соответственно блока сложения-вычитания и блоков вычисления коэффициентов корреляции для случая m 4, п 16. На фиг. 4 и 5 приведены схемы соответственно блока вычисления коэффициентов корреляции и блока определения номера коэффициента корреляции для того же случая.
Декодер содержит: входной буферный регистр 1, блоки вычитания 2, блоки вычисления коэффициентов корреляции 3, блок сравнения 4, блок ключей 5, блок определения номера максимального коэффициента корреляции 6, блок сложения-вычитания двух элементов 7, нуль-орган 8. выходной буферный регистр 9.
Буферный регистр 1 представляет собой 2т-разрядный регистр
Блок сложения-эычитэния 2 (фиг. 2) для i-ro шага (i Ј т-2) содержит сумматоров 10 и вычитателей 11.
Блок вычисления коэффициентов корреляции 3 (фиг. 4), содержит элементы сравнения 12, элементы запрета И 14, сумматоры 15 и вычитатель 16. Блок сравнения 4 определяет номер максимального коэффициента корреляции.
Блок ключей 5 пропускает на вход блока 6 элементы, давшие максимальный коэффициент корреляции в блоках 3.
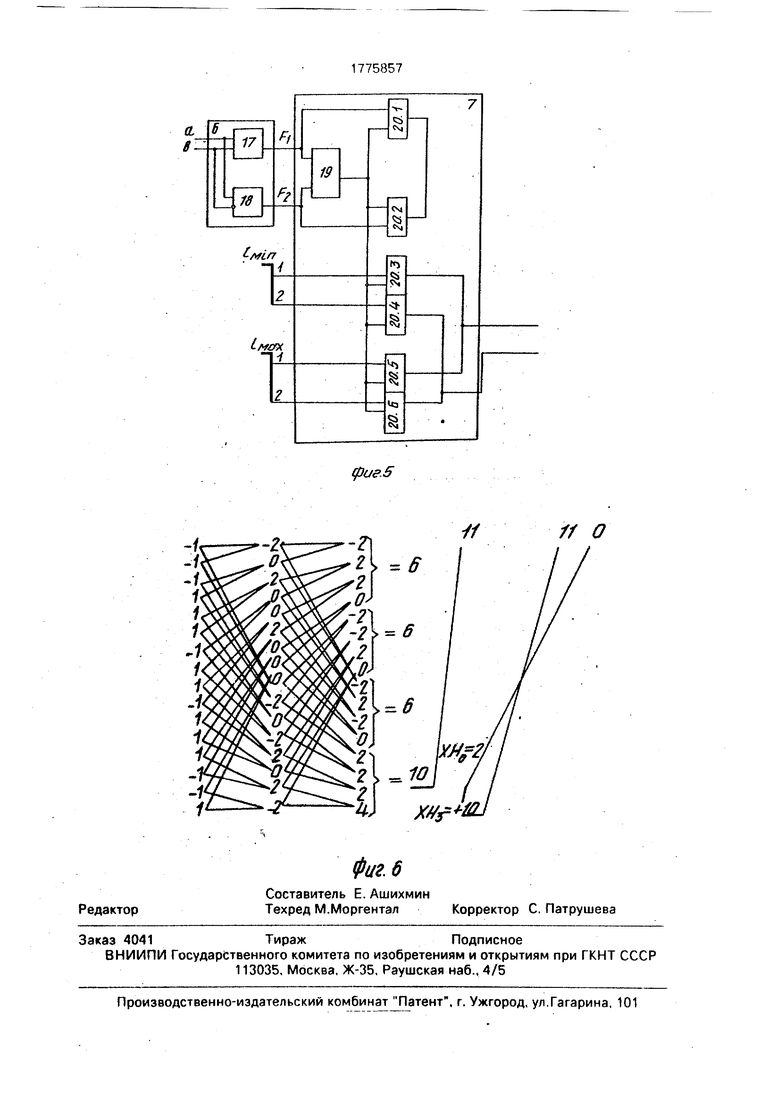
0 Блок определения номера максимального коэффициента корреляции б содержит элемент сравнения 19 и элементы И 20 (фиг. 5).
Блок сложения-вычитания двух элемен5 тов 7 состоит (фиг. 5) из сумматора 17 и вычитателя 18.
Нуль-орган 8 представляет собой блок определения знака числа.
Выходной буферный регистр 9 пред0 ставляет собой (т+1)-разрядный буферный регистр.
Идея упрощения декодера заключается в следующем. Первые т-2 этапов декодирования совпадают с аналогичными этапами в
5 прототипе: осуществляется попарное сложение и вычитание элементов а и ан-1, i 1,3,5...,п-1. Затем полученная последовательность длины п разбивается на группы по четыре элемента в каждой. В каждой из
0 этих подгрупп вычисляется максимальный коэффициент корреляции, среди полученных коэффициентов корреляции находится максимальный по модулю коэффициент корреляции, двоичный номер группы, в которой
5 он получен дает (3-т) информационные символы. Так как по четырем элементам любой группы можно найти четыре коэффициента корреляции, то номер максимального из них, в группе пропущенной на дальней0 шее декодирование, дает первый и второй информационные символы. Знак максимального по модулю коэффициента корреляции дает (т + 1)-й информационный символ.
5Максимальный коэффициент корреля ции в группе из четырех элементов находится следующим образом. Пусть мы имеем элементы хо, XL X2, хз - которые составляют одну из групп после (т-2) этапов декодиро0 вания. Для вычисления коэффициентов корреляции необходимо умножить вектор х (хо. xi, X2, хз) на транспонированную матрицу Адамара Н размерности 4x4. Выберем в качестве этой матрицы матрицу:
5-111 -1
1-1 1-1 Н 11-1-1
1111
Можно заметить, что любая строка этой матрицы не совпадает с вектором г (1. 1, 1, -1)
лишь в одной позиции, причем, 1-я строка матрицы Н не совпадает с вектором Z в i-ой позиции. Таким образом, если мы вычислим величину у x.z хо + xi + Х2 - хз, то величины
ko Х Но -ХО + Х1 - Х2 ХЗ
ki x-Hi хо - xi + Х2 - хз ka х Н2 хо xi - х - хз
k3 Х-Нз ХО + Х1 + Х2 + ХЗ
где ki - i-й коэффициент корреляции, Hi - 1-я стока матриц Н, и величина у будут связаны соотношениями:
ko у + 2 хо
ki y + 2 xi
К2 у + 2х2
кз у + 2 хз
Величина у является постоянной для постоянных хо, xi, X2, хз, следовательно, максимальный коэффициент корреляции возникнет там, где к величине у прибавля- ется максимальный элемент xi или наоборот минимальный элемент xi, причем максимальный и минимальный элементы следует искать среди элементов хо, xi, Х2, -хз, т.к. кз у - . Далее, если максимальный и минимальный элементы имеют номера Imax и Imin, то в выражении (1) для kimax и kimln элементы ximax и ximin берутся с разными знаками (в этом можно убедиться при непосредственной проверке матрицы Н), а два оставшихся элемента берутся со знаком плюс (все операции проводятся над элементами хо, xi, X2, -хз). Окончательно, если имеем элементы хо, xi, X2, хз, то для нахождения kmax max (ko, ki, k2, кз), необходимо найти максимальный и минимальный элементы хо, xi, X2, -хз и соответственно их номера Imax и Imin, затем вычислить величину yi xmax -Xmin И Величину Y2 Хс - Xd, С Hmax. Imin, d С, Imax. Imin, и Kmax |yi (во всех ВЫЧИС-
лениях хз берется со знаком минус).
Поясним вышесказанное на примере. Пусть декодируется вектор: w (-1 -1-111 1-111-1-111-1-1 1), тогда граф декоди- рования будет иметь вид, показанный на фиг. 6. Рассмотрим нахождение максимальных коэффициентов корреляции в каждой группе:
1.хо -2, xi 2, Х2 2, -хз 0. Ищем максимальные и минимальные элементы
Xmax 2, Xmin -2, Imin 1. Imax 0. У1 XI - X0 4, V2 - X2 X3 -2
Kmaxu 4 + 2 6
2.xo -2, xi -2, х2 2,-хз 0
Xmax 2, Xmin 2, Imax 2, Imin 0 yi xi - xo 4, Y2. X2 - хз -2 k1max 4 + 2 6
3. xo -2, xi 2, X2 -2, -хз О
Xmax 2, Xmin 2, Imax 1, Imin 0
5
0
5
0 5 0 5
0
0
5
yi xo - xi 4, y2 xa - хз - -2 k2max 4 + 2 6 4. xo 2, xi 2, X2 2, -хз 4 Xmax 2, Xmin 4, Imax 0, Imin 3
У1 XO XI 6, У2 X2 + X3 4, k
3
10
Таким Образом. k3max k°max, k1max,
k max, и, следовательно, 3-й и 4-й информационных символа это: 1,1. Далее необходимо определить номер максимального коэффициента в своей группе, т.е. какая строка матрицы Н при умножении х.Нт дала максимальный коэффициент корреляции, Это может быть строка с номером 0 или 3, т.к. Imax 0, Imin 3. При умножении на нулевую строку будем иметь величину -6 + +4 -2. при умножении на третью строку величину 6 + 4 10, следовательно, максимальный коэффициент даст третья строка, т.е. первый и второй информационные символы: 1 1. Общее правило нахождения номера максимального коэффициента корреляции (т.е. строки матрицы Н дающей максимальный коэффициент корреляции) следующее. Допустим, мы вычислили kmax lyil + Iy2l , Imax, Imin, затем вычисляем величины oi -yi + у2, дг yi + У2, сравниваем д и О2, если(1 02, то номер строки дающей максимальный коэффициент корреляции - это Imfn, в противном случае это Imin, двоичное представление или Imax дают первый и второй информационные символы.
Работает декодер кода Рида-Маллера следующим образом. Кодовый вектор длины n 2m приходит из линии связи и записывается в буферный регистр 1, оттуда элементы вектора подаются на вход блока сложения- вычитания 2.1. Результаты суммирования сумматоров 10 и вычитателей 11 i-ro блока сложения-вычитания 2.I (I 1, m - 3) подаются на входы (I + 1)-го блока сложения-вычитания 2.1 + 1. Элементы с т-2 блоков сложения-вычитания подаются на блоки зычисления коэффициентов корреляции 3, по четыре последовательных элемента на каждый блок. В блоке 3 (фиг. 4) происходят следующие действия. Элемент хз инвертируется, затем сравниваются элементы хо и xi, X2 и (-хз). Элемент 12 сравнения имеет на выходе логическую единицу,если хо xi (х2 (-хз)) и логический ноль, если хо xi (X2 (-хз)). Тогда посредством элементов 13, 14 на шины maxi, max2 пропускаются большие из элементов хо и xi (x2 и (-хз)), а на шины mini, min.2 соответственно меньшие элементы. Затем происходит сравнение максимального элемента среди элементов хо и xi с максимальным элементом среди элементов Х2 и (-хз), сравнение максимального элемента среди (хо и xi) с минимальным
элементом среди (х и (-хз)) Таким образом, мы находим Хтах и Xmin, которые поступают по шинам max и min на вычитатель 16, на выходе которого получаем величину yi. По шинам с и d на сумматор 15 1 поступают хс и хь
где Climax, Imln, d С, Imax, Imln. НЭ ВЫХОДе
этого сумматора получаем величину уа Величины yi, и уа поступают на сумматор 15.2 на выходе которого мы имеем величину kmax Hyil + lyal . Величины kmax поступают в блок сравнения 4. Одновременно с помощью элементов И 14 на шинах Цах и Imln формируются двоичные номера величин хтах и
Xmlnl Imax И Imln. Затем yi И уа, Imax И Imin
каждой группы из четырех элементов поступают на блок ключей 5. В блоке сравнения 4 происходит определение номера максимального коэффициента среди коэффициентов, пришедших со всех групп по четыре элемента каждая. Двоичный номер максимального коэффициента - это (3-т)-е информационные символы, они подаются в выходной буферный регистр 9, кроме того они подаются в блок ключей 5 и определяют, из какой группы пропустить на дальнейшее декодирование элементы yi, уа, Imax и Imln. Пропущенные элементы yi, уа подаются на блок сложения и вычитания двух элементов 7 (фиг. 5), в котором определяются величины д yj + уа и дг - - уч + уа. Величины di и д подаются на блок определения номера максимального коэффициента корреляции б, туда же поступают элементы Imax и lmtn с выходов блока ключей 5. В блоке определения номера максимального коэффициента корреляции 6 сравниваются величины и l&l , если dz, то на первый и второй входы выходного буферного регистра 9 подается величина Imln, в противном случае величина Imax; кроме того большая по модулю из величин Ic5il и Idal поступает на вход нуль-органа 3, где определяется
знак этой величины; если знак плюс, то выход нуль-органа д равен нулю, в противном случае он равен единице. Символ с выхода нуль-органа 8 подается на (т + 1)-й вход
выходного буферного регистра 9.
Формула изобретения Декодер кода Рида-Маллера первого порядка по максимуму правдоподобия, содержащий последовательно соединенные
входной буферный регистр и первый - (т- 2)-й блоки сложения-вычитания (2т - длина кода Рида-Маллера, т 1,2,...), блок сравнения, выходы которого соединены с управляющими входами блока ключей, первые
выходы которого подключены к входам блока сложения-вычитания двух элементов, нуль-орган, выход которого соединен с входом (m+1)-ro разряда выходного буферного регистра, входы входного и выходы выходчого буферных регистров являются соответственно входами и выходами декодера, о т- личающийся тем, что, с целью упрощения декодера в него введены первый - ()-й блоки вычисления коэффициентов корреляЦии и блок определения номера максимального коэффициента корреляции, выходы (т-2)-гоблока сложения-вычитания подключены к входам первого -()-го блока вычисления коэффициентов корреляции,
первые и вторые выходы которых соединены соответственно с входами сравнения и информационными входами блока ключей, выходы блока сложения-вычитания двух элементов и вторые выходы блока ключей
соединены с первыми и вторыми входами блока определения номера максимального коэффициента корреляции, первый, второй и третий выходы которого подключены соответственно к входу нуль-органа и входам
первого и второго разрядов выходного буферного регистра, входы третьего - т-го разрядов которого подключены к выходам блока сравнения.



| название | год | авторы | номер документа |
|---|---|---|---|
| Декодер кода Нордстрома-Робинсона | 1990 |
|
SU1797164A1 |
| Устройство для декодирования кода Нордстрома-Робинсона в дискретном канале | 1989 |
|
SU1736008A1 |
| Кодек на основе кода Рида - Маллера первого порядка | 1990 |
|
SU1777243A1 |
| Декодер кодов Рида-Маллера первого порядка | 1987 |
|
SU1474854A1 |
| Устройство управления самоходным средством | 1988 |
|
SU1689921A1 |
| Непосредственный преобразователь частоты | 1990 |
|
SU1837377A1 |
| Устройство для вычисления дискретного преобразования Фурье | 1987 |
|
SU1425708A1 |
| Способ измерения аналоговой величины с коррекцией результата | 1989 |
|
SU1672563A1 |
| Система передачи информации перфорированным сверточным кодом с восьмифазной модуляцией | 1990 |
|
SU1795499A1 |
| Коммутатор- распределитель экстремального сигнала | 1989 |
|
SU1622888A1 |

Изобретение относится к вычислительной технике. Его использование в аппаратуре передачи дискретной информации позволяет упростить декодер, содержащий входной буферный регистр 1, блоки сложения-вычитания, блок сравнения, блок ключей, блок сложения-вычитания двух элементов, нуль-орган и выходной буферный регистр. Благодаря введению блоков вычисления коэффициентов корреляции и блока определения номера максимального коэффициента корреляции в декодере сокращается число блоков сложения-вычитания. 6 ил.
фаг. /
фиг 2
а.
Iferx
fifl/7
фе/гЬ
1
Редактор
Составитель Е. Ашихмин Техред М.Моргентал
cpueS
// О
XVf
Фаг. 6
Корректор С Патрушева
| Проблемы передачи информации, 1983, т | |||
| Способ изготовления электрических сопротивлений посредством осаждения слоя проводника на поверхности изолятора | 1921 |
|
SU19A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Авторское свидетельство СССР № 1568251,кл | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1992-11-15—Публикация
1990-07-09—Подача