ел С


| название | год | авторы | номер документа |
|---|---|---|---|
| Декодер кода Рида-Маллера первого порядка по максимуму правдоподобия | 1990 |
|
SU1775857A1 |
| Устройство для декодирования кода Нордстрома-Робинсона в дискретном канале | 1989 |
|
SU1736008A1 |
| Декодер кодов Рида-Маллера первого порядка | 1987 |
|
SU1474854A1 |
| Устройство для формирования изображений на экране телевизионного индикатора | 1982 |
|
SU1336092A1 |
| СПОСОБ ДЕКОДИРОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ, РАСПРОСТРАНЯЮЩИХСЯ В МНОГОЛУЧЕВОМ КАНАЛЕ | 2014 |
|
RU2550086C1 |
| Кодек на основе кода Рида - Маллера первого порядка | 1990 |
|
SU1777243A1 |
| Устройство для приема и градиентного декодирования избыточных сигналов | 1983 |
|
SU1152016A1 |
| Кодер телевизионного сигнала | 1990 |
|
SU1753596A2 |
| Устройство для вычисления дискретного преобразования Фурье | 1987 |
|
SU1425708A1 |
| Адаптивное устройство для приема избыточной информации | 1981 |
|
SU1001145A1 |

Изобретение относится к вычислительной технике. Его использование в системах передачи дискретной информации позволяет расширить область применения за счет декодирования в полунепрерывном канале и упростить декодер, который содержит блоки сложения-вычитания 1, блок сравнения 3, блок ключей 4, блок сложения и вычитания двух элементов 5, нуль-орган 7 и выходной буферный регистр 8. Благодаря введению 32 блоков вычисления коэффициентов корреляции 2 и блока определения номера максимального коэффициента корреляции 6 обеспечивается значительное сокращение числа сумматоров по сравнению с прототипом. 7 ил.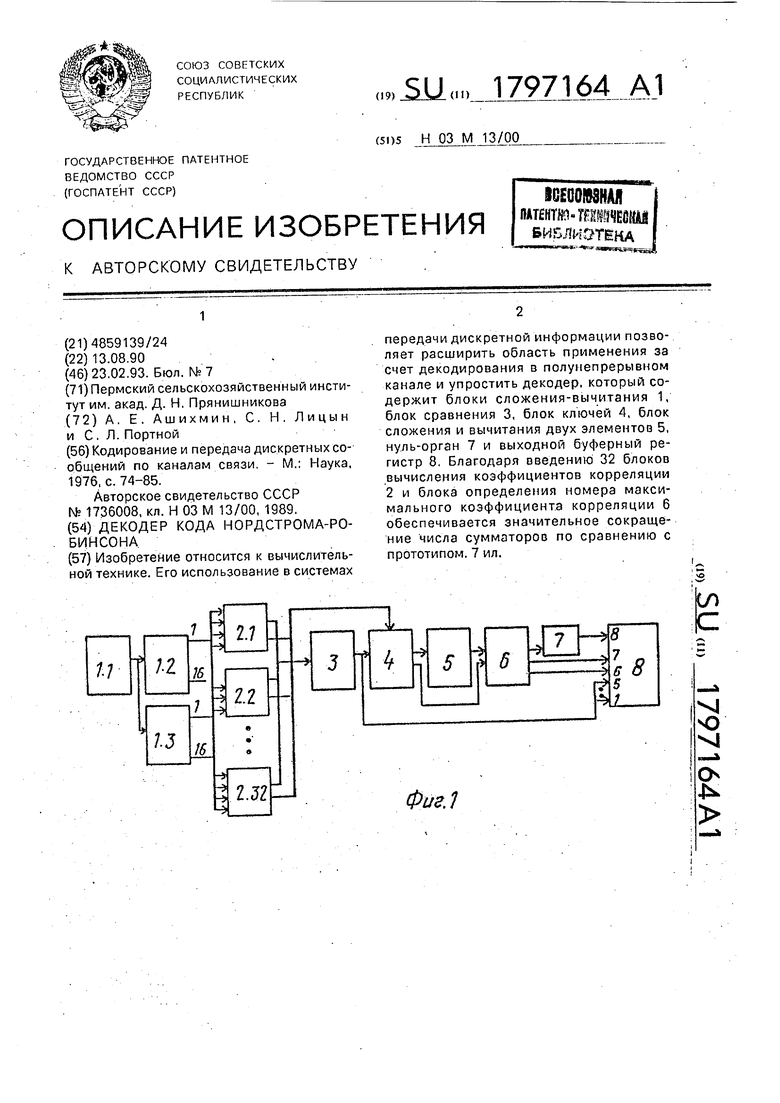
чэ ч
(
4
Изобретение относится к вычислительной технике, конкретно к устройствам декодирования кода Нордстрома-Робинсона.
Известно устройство декодирования кода Нордстрома-Робинсона, основанное на разбиении кода на биортогональные под- коды с помощью преобразования Уолша. Данное устройство предназначено для декодирования широкого класса кодов, разбивающихся на биортогональные, и для кода Нордстрома-Робмнсона не является оптимальным. . .
Устройство содержит восемь блоков декодирования биортогонального кода, основанных на быстром преобразовании Уолша, и схемы выбора максимального элемента.
Наиболее близким к предлагаемому устройству является устройство декодирования кода Нррдстрома-Робинсона, основанное на разбиении кода Нордстрома-Робинсона на смежные классы по коду Ридамаллера первого порядка и проведении в каждом смежном классе усеченного быстрого преобразования Уолша. Данное устройство обеспечивает декодирование по максимуму правдоподобия лишь в дискретном канале, кроме того, оно не учитывает тождественные вычисления в различных смежных классах и следовательно не является оптимальным.
Это устройство содержит семь блоков сложения с образующим смежного класса, усеченные декодеры кода Рида-Маллера, блок ключей, блок сравнения, регистр записи декодированного слова.
Целью изобретения является декодер кода Нордстрома-Робинсона.
Эта цель достигается тем, что в декодер кода Нордстрома-Робинсона, содержащий пёрвый-третий блоки сложения-вычитания, входы первого блока сложения-вычитания являются входами декодера, блок, сравнения, выходы которого соединены с управля- ющими входами блока ключей и первым-пятым входами выходного буферного регистра, выходы которого являются выходами декодера, блок сложения и вычитания двух элементов и нуль-орган, введены первый - 32-й блоки вычисления коэффициентов корреляции и блок определения номера максимального коэффициента корреляции, выходы первого блока сложения-вычитания подключены к соответствующим входам второго и третьего блоков сложения-вычитания, выходы которых соединены с соответствующими входами всех блоков вычисления коэффициентов корреляции, первые и вторые выходы которых подключены соответственно ко входам блока сравнения и информационным входам
блока ключей, первые выходы которого соединены со входами блока сложения и вычитания двух элементов, выходы которого и вторые выходы блока ключей подключены к
первым и вторым входам блока определения номера максимального коэффициента корреляции, первый, второй и третий выходы которого соединены соответственно со входом нуль-органа и .шестым и седьмым
О входами выходного буферного регистра, выход нуль-органа подключен к восьмому входу буферного регистра.
Благодаря тому, что на первых двух этапах учитываются одинаковые операции сло5 жения и вычитания в различных смежных классах и благодаря тому, что после второго этапа вычисляются.сразу максимальные коэффициенты корреляции в группах по четыре элемента в каждой, число сумматоров
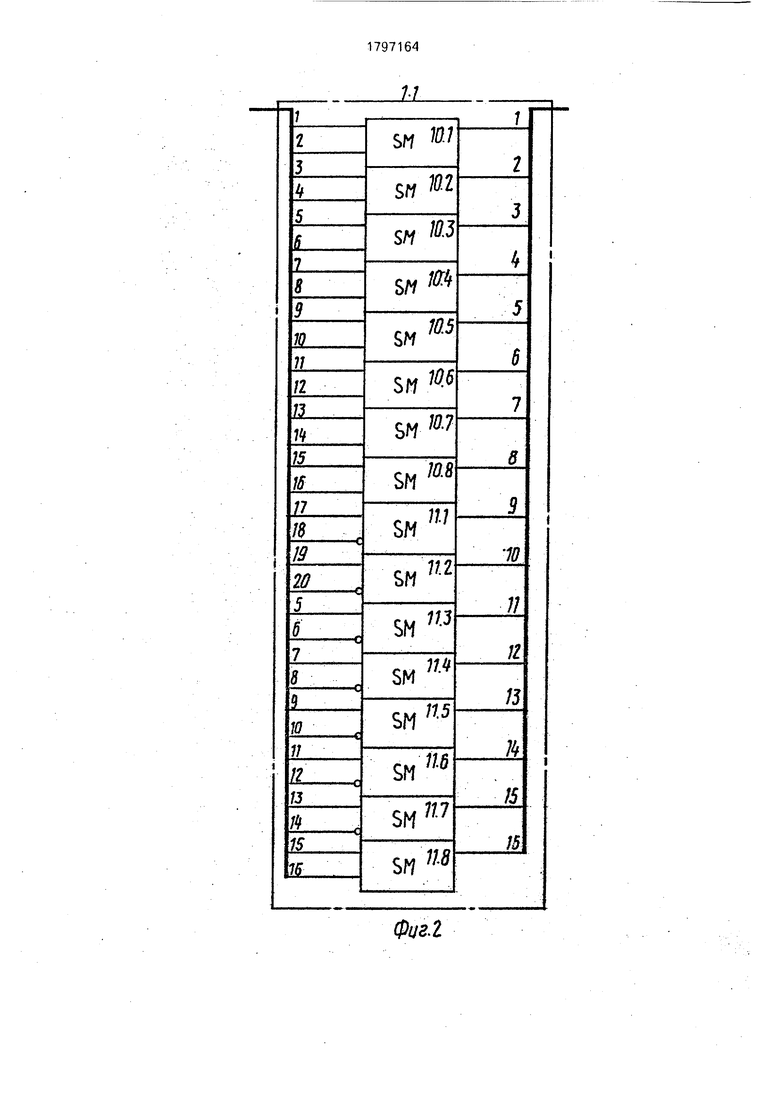
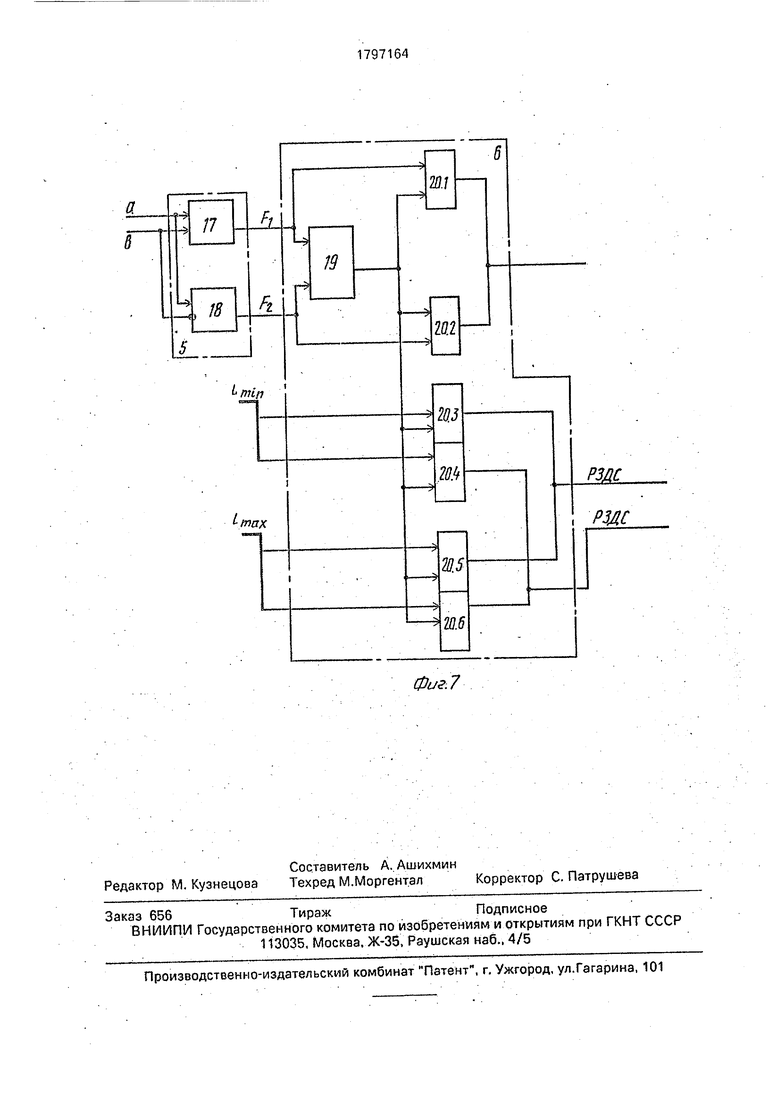
0 уменьшается с 512 до 144. На фиг. 1 изображена структурная схема декодера. На фиг. 2-7- возможные реализации соответствующих блоков.
Декодер (фиг, 1) содержит блоки сложе5 ния-вычитания1, блоки вычисления коэффициентов корреляции 2, блок сравнения 3, блок ключей 4, блок сложения и вычитания двух элементов 5, блок определения номера максимального коэффициента корреляции
0 6, нуль-орган 7, выходной буферный регистр 8. Блоки сложения-вычитания 1 (фиг. 2, 3) содержат сумматоры 10 и вычитатели 11.
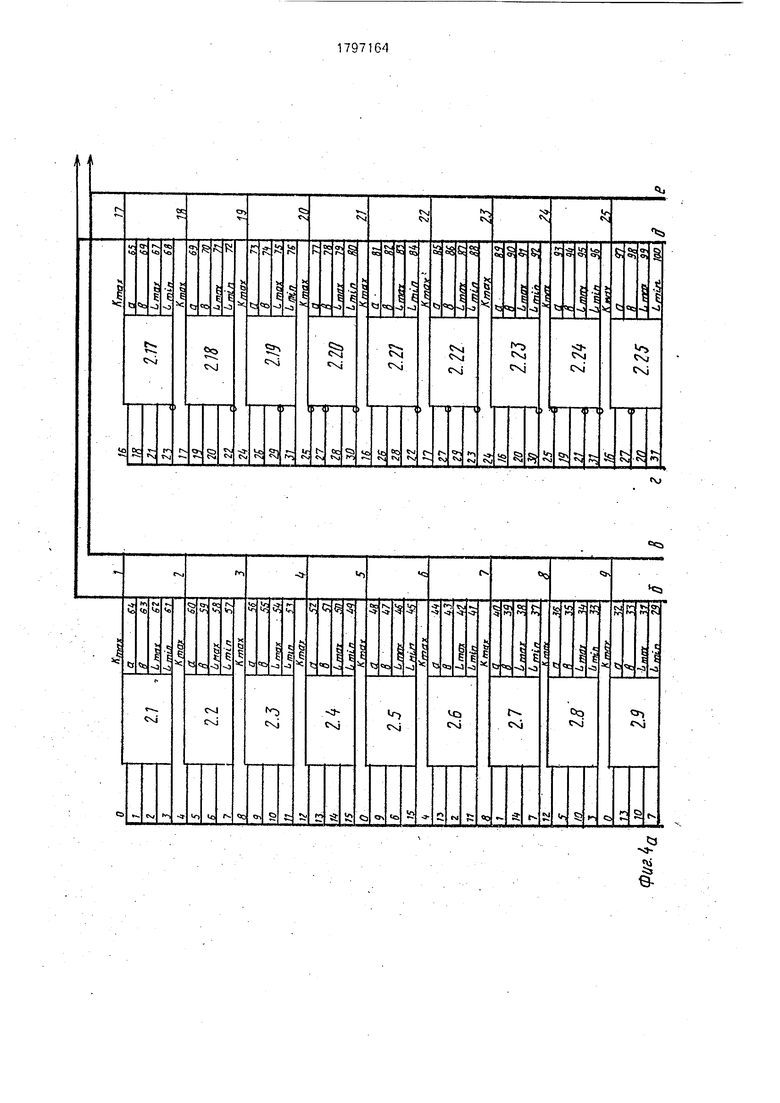
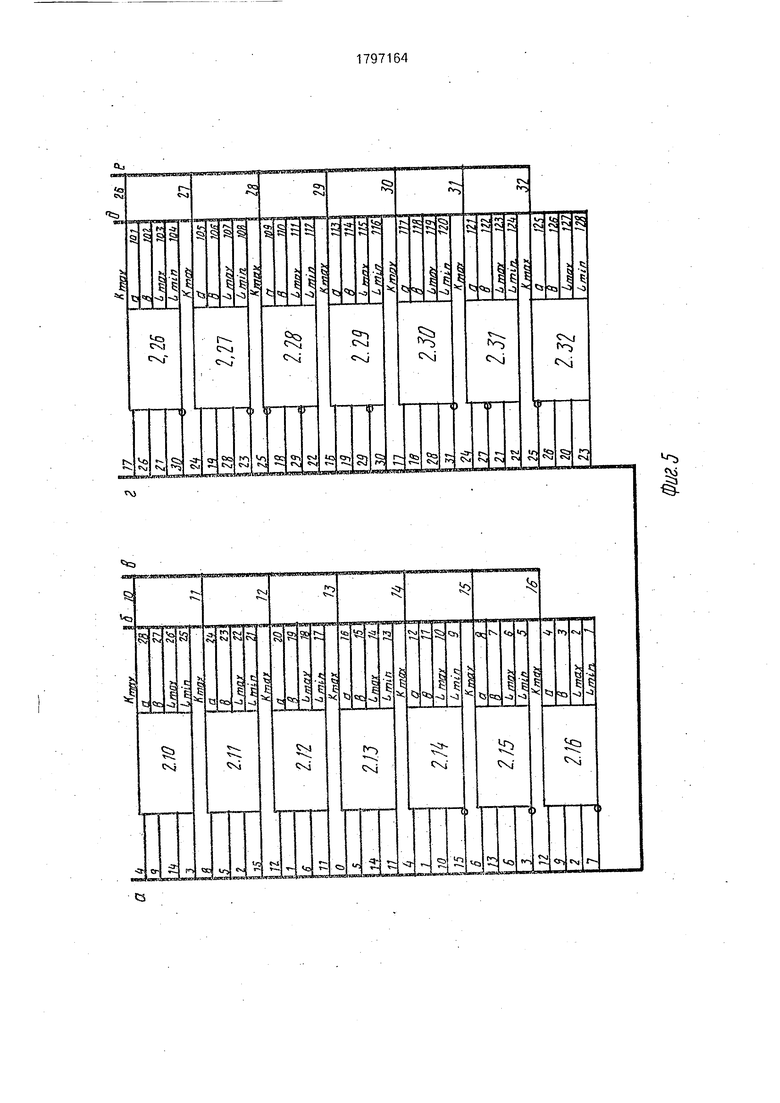
Блоки вычисления коэффициентов корреляции 2 (фит, 4, 5) 6 состоят из четырех
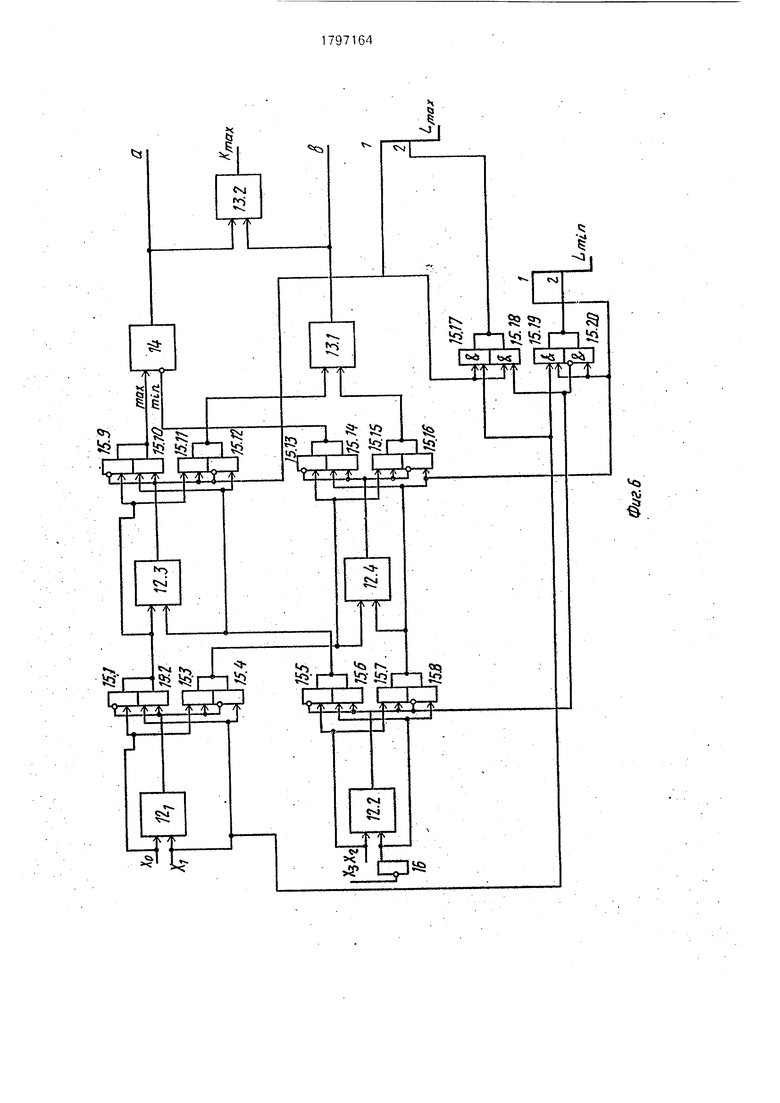
5 двухвходовых элементов сравнения 12, двух сумматоров 13, вычитателя 14, двадцати элементов И 15. Инвертирование соответствующего входного сигнала обеспечивается элементами НЕ 16.
0 Блок сравнения 3 выполнен на элементах И, ИЛИ, НЕ и выделяет номер максимального коэффициента корреляции. Блок сложения и вычитания двух элементов 5 (фиг. 7) состоит из сумматора 17 и вычитате5 ля 18. Блок номера максимального коэффициента корреляции 6 состоит (фиг. 7) из элемента сравнения 19 и элементов И 20. Нуль-орган 7 представляет собой устройство определения знака числа. Выходной бу0 ферный регистр 8 представляет собой восьми разрядный буферный регистр.
Идея упрощения декодера заключается в следующем. Код Нордстрома-Робинсона разбивается на 8 смежных классов по коду
5 Рида-Маллера первого порядка. Таким об- разом достаточно продекодировать восемь раз принятый вектор, к которому прибавлен Очередной образующий смежного класса, и выбирать среди полученных 128 коэффици- ентов корреляции (по 16 коэффициентов
корреляции в каждом смежном классе) максимальный коэффициент. Двоичный номер этого коэффициента даст 8 информационных символов.
Но на первых двух этапах декодирования кодов Рида-Маллера первого порядка в различных смежных классах имеется значительное количество одинаковых вычислений. Таким образом можно ограничиться шестнадцатью сложениями на первом этапе и 32-мя сложениями на втором этапе декодирования. После второго этапа имеем 128 элементов (по 16 элементов в восьми смежных классах). Разбиваем эти 128 элементов на группы по четыре последовательных элемента в каждой и определяем в каждой группе максимальный коэффициент корреляции. Для нахождения максимального коэффициента корреляции в группе из четырех элементов требуется три сумматора, т.е. всего потребуется 3 сумматоров. Если же производить вычисления в полном обьеме, то потребуется 512 сумматоров. Таким образом количество сумматоров значительно уменьшается.
Максимальный коэффициент корреляции в группе из четырех элементов находится следующим образом. Пусть мы имеем элементы Хо, Хь Х2. Хз в одной из групп после второго этапа декодирования. Для вычисления коэффициентов корреляции необходимо умножить вектор х(хо, XL X2, хз) на транспонированную матрицу Адамара Н размерности 4x4. Выберем в качестве этой матрицы матрицу: -1 11-1
Н 1 -1 1 -1 11-1-1 .1111..
Можно заметить, что любая строка этой матрицы не совпадает с вектором z(1,1,1, -1) лишь в одной позиции, причем 1-я строка матрицы Н не совпадает с вектором z в 1-ой позиции. Таким образом, если мы имеем величину Z xi+x2+x3+x4 и величины:
-Но -Х0+Х1+Х2-Хз
Н1 Хо-Х1+Х2-Хз
-Н2 Хо+Х1-Х2-Хз
-Нз Хо+Х1+Х2+Хз, где ki это 1-й коэффициент корреляции (среди этих коэффициентов нам необходимо найти максимальный, HI это 1-я строка матрицы Н). то величину у и ko, ki, k2, k3 будут связаны соотношениями:
1 о у+2хо
ki y+2xt
k2 y+2x2
(-x3)
Величина у является постоянной для постоянных хо. XL X2, хз. Следовательно максимальный по модулю коэффициент корреляции kmax max (|k0l, 1Ы. 1Ы, 1кз1) возникает там. где к величине у прибавляется максимальный
элемент (xo,xi, Х2,-хз)или наоборот минимальный элемент xminr:rmin(x, x, х, -х) (элемент хз берется со знаком минус, так как (-х)). Таким образом kmax может появиться при умножении вектора х либо на
строку которая не совпадает с вектором z в позиции, где расположен элемент хтах, либо приумножении на строку, которая не совпадает стзектором z в позиции, где расположен элемент Xmin. Далее если максимальный и
минимальный элементы имеют номера Imax и Imin, то в соответствующих выражениях для коэффициентов корреляции kimax, kimin элементы xmax и Xmin берутся с разными знаками (в этом можно убедиться при непосродственной проверке матрицы Н), а два
оставшихся элемента берутся со знаком плюс (осе операции производятся над элементами (хо, XL X2, -хз). Окончательно, если мы имеем элементы хо, XL X2. -Х2, то для
нахождения kmax необходимо найти Хтах и Xmin, а также их номера Imax и Imin, затем
ВЫЧИСЛИТЬ у Хтах-Хщ|п. } Xc+Xd, С
, Imin. d &C, Imax, Imin, И kmax I У1 I + I Y2 I .
Поясним вышесказанное на примере. Пусть декодируется вектор W-(1 -1-1111
-111-1111-1-1 1). На выходе блока 1.1
будем иметь вектор W(0 02002002-20
-22022). На выходе блоков 1.2, 1.3 будем
иметь вектор: W(0 2200-22002-2042
240244020002004-200-204-220
02240-2200-2-2402200-2200-22
-04-2-200-2244-2200-2200202-20 02-200-22442-20. -20022002204
-224020-22002-2-402204220).
Рассмотрим нахождение максимального коэффициента корреляции в первой группе из четырех элементов. Первые четыре элемента в данном случае: 0220, т.е. ,
, , . Они поступают на вход первого блока вычисления коэффициента корреляции 2.1 (фиг. 3). В блоке элементы хо и хг(х2 и (-хз)) сравниваются элементом сравнения 12.1 (12(2)), на выходе которого появляется логическая единица, если ()), и логический ноль в противном случае. Элементсравнения 12.3 сравнивает больший элемент среди элементов хо и х-1 с большим элементом среди элементов Х2
ц (-хз). Таким образом на шине max появляется Xmax: max(xo, Х1..х2-хз), а на шине min элемент (xo, XL Х2, -хз), которые вычитаются в Бычитателе 14, т.е. иа шине а мы
получим величину yi. Аналогичным образом на шине b получается величина уг. С помощью ключей, выполненных на базе элементов И 15, на шинах 1тах формируется величина Imax в двоичном коде, а на шинах Imin величина lmin, также в двоичном коде. Сумматор 13.2 осуществляет сложение модулей величин, поступающих на его входы т.е. находит Kmax I yi I 4- I уг В нашем примере
, , , , . .
Таким образом на выходе блока вычисления коэффициентов корреляции 2 вычисляется вектор коэффициентов корреляций: (44412 10226848484484844448844884 8 48), который поступает на вход блока сравнения 3. Блок сравнения 3 определяет двоичный номер максимального коэффициента корреляции. На выходе блока сравнения 3 имеем вектор (0001 1), элементы которого подаются на первый-пятый входы выходного буферного регистра 9 соответственно. Они также поступают на блок ключей 4 и определяют, для какой группы пропустить на дальнейшее декодирование величины, у , уа, Imax, imin. В нашем случае: ,
, , .
Далее необходимо установить, при умножении на какую строку матрицы Не номером Imax ИЛИ на Строку С Номером Imin
получается элемент kmax. При умножении на нулевую строку вектора х(4 2 2 -4) (вектор, который дал максимальный коэффициент корреляции) получаем , при умножении на третью строку получаем (элемент хз везде берется со знаком минус), Номер
Фа рмул а изобретен и. я Декодер кода Нордстрома-Робинсона, содержащий первый-третий блоки сложения-вычитания, входы первого блока сложения-вычитания являются входами декодера, блок сравнения, выходы которого соединены с управляющими входами блока ключей и первым-пятым входами выходного буферного регистра, выходы которого являются выходами декодера, блок сложения и вычитания двух элементов и нуль-орган , о т л и ч а ю щ и и с я тем, что, с целью расширения области применения за счет декодирования в полунепрерывном канале и упрощения декодера, в него введены первый - тридцать второй блоки вычисления коэффициентов корреляции и блок определения нбмера максимального коэффициента корреляции, выходы первого блока Сложения-вычитания подключены к соответстроки, где получался максимальный коэффициент, даст шестой и седьмой информационные символы. Строки с номерами Imin и
max различаются тем, что в одной из них при
вычислении коэффициента корреляции yi берется с плюсом, а в другой с минусом. Поэтому один коэффициент будет равен У1 +Уа, а другой- yi + уг. Данная операция осуществляется в блоке сложения и вычитания двух элементов 5. На выходе этого блока будем иметь 12 и -4. Причем если I yi I + I У2 I I -yi + уа I , то номер строки, дающей Ктах, - это Imin, в противном случае это Imax (последнее утверждение
проверяется непосредственной проверкой). Величины yi + у2, 12 и - yi 4- уа, -4 с выходов блока суммирования и вычитания двух элементов 5 поступают на вход блока определения номера максимального коэффициента корреляции 6, где происходит сравнениеI yi + уа I и I У + уа I , и в зависимости от результатов сравнения на выходной буферный регистр 9 пропускается Либо Imin, Либо Imax. В
нашем примере пропускается на шестой и седьмой входы выходного буферного регистра 9. Кроме того в зависимости от сравнения на нуль-орган 7 пропускается либо yi +У2, , либо - yi +у2, . В нашем случае пропускается у + уа 12. Нуль-орган 7 определяет знак входной величины и выдает ноль в случае положительной величины и единицу в случае отрицательной величины. В нашем случае на выходе нуль-органа 7 появляется ноль, который подается на восьмой вход регистра 9.
ствующим входам второго и третьего блоков сложения-вычитания, выходы которых соединены.с соответствующими входами всех блоков вычисления коэффициентов корреляции, первые и вторые выходы которых подключены соответственно к входам блока сравнения и информационным входам блока ключей, первые выходы которого соединены с входами блока сложения и вычитания двух элементов, выходы которого и вторые выходы блока ключей подключены к первым и вторым входам блока определения номера максимального коэффициента корреляции, первый, второй и третий выходы которого соединены соответственно с входом нуль-органа, шестым и седьмым входами выходного буферного регистра, выход нуль-органа подключен к восьмому входу выходного буферного регистра.
b9U6M
Фиг.Ъ
Фи г. 7
| Кодирование и передача дискретных сообщений по каналам связи | |||
| - М,: Наука, 1976, с | |||
| Приспособление в центрифугах для регулирования количества жидкости или газа, оставляемых в обрабатываемом в формах материале, в особенности при пробеливании рафинада | 0 |
|
SU74A1 |
| Устройство для декодирования кода Нордстрома-Робинсона в дискретном канале | 1989 |
|
SU1736008A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1993-02-23—Публикация
1990-08-13—Подача