Существующие устройства для моделирования систем линейных алгебраических уравнений представляют собой линейные электрические цепи, к определенным точкам которых приложены уравновешивающие напряжения, изменяемые до тех пор, пока не обратятся в нуль напряжения невязок в других точках схемы.
Известны устройства с неизбежной сходимостью процесса уравновешивания, в которых каждый коэффициент уравнений моделируется одной проводимостью. Такие модели содержат параметрические элементы, т.е. линейные элементы, параметры которых изменяются во времени по одинаковому закону (например, синхронно работающие контакты реле). Они дороги и ненадежны.
Предложенное устройство отличается от известных тем, что оно содержит источники синусоидального напряжения, соединенные через резисторы с электрической цепью в точках приложения уравновешивающих напряжений, и диоды, подключенные к электрической цепи в точки образования невязок моделируемых уравнений.
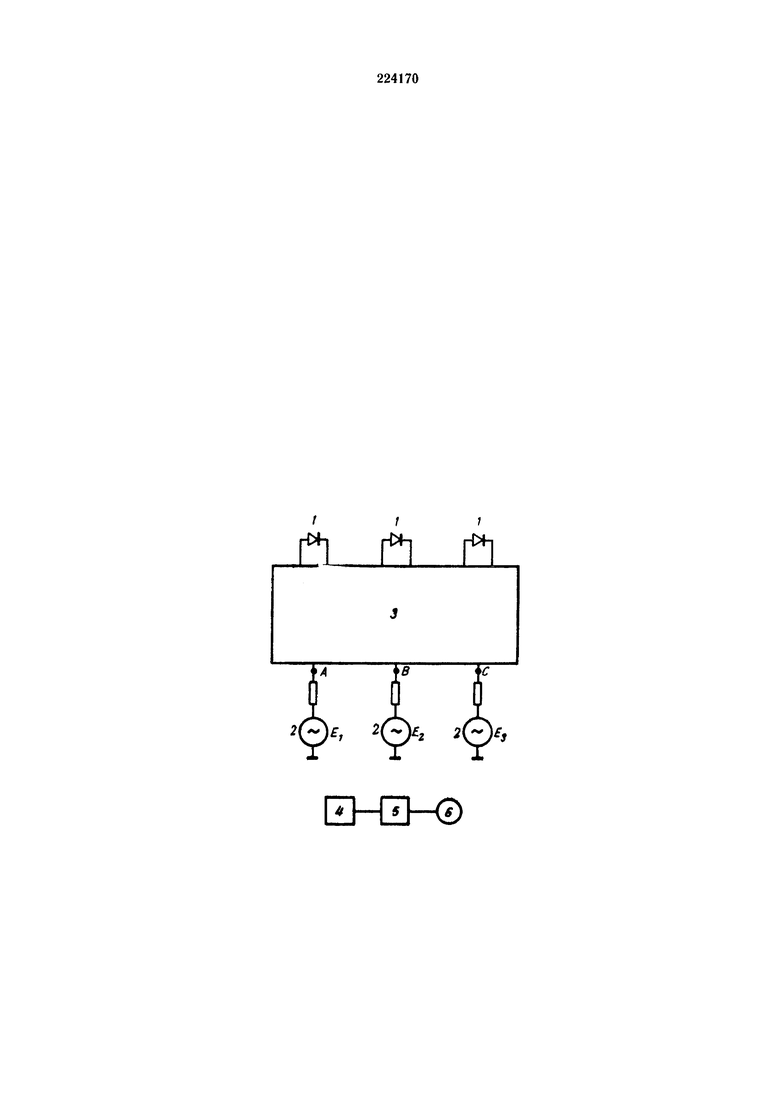
На чертеже дана схема устройства.
Спектор сигнала преобразуется с помощью нелинейных элементов 1 (например, диодов) и источников синусоидального напряжения 2 (Е1, Е2, Е3), которые создают в точках А, В, С уравновешивающие напряжения первой гармоники. Диоды включены между теми точками цепи, которые в процессе уравновешивания должны быть сделаны эквипотенциальными. Матрица взаимных проводимостей электрической цепи 3 используется дважды: при прохождении сигналов первой гармоники от источников 2 к диодам 1 и при прохождении сигналов других гармоник от диодов 1 к источникам 2. Диоды потребляют энергию первой гармоники и при этом генерируют сигналы третьей гармоники, нулевой гармоники (постоянной составляющей) и других гармоник. Эти сигналы распространяются по цепи в обратном направлении и достигают точек А, В, С. Для обнаружения этих сигналов к точкам А, В, С поочередно подключается нуль-орган, содержащий фильтр 4, усилитель 5 и измерительный прибор 6.
Величина напряжения E1 регулируется так, чтобы нуль-орган, подключенный к точке A, показал нуль, затем напряжение Е2 регулируется так, чтобы нуль-орган показал нуль в точке B и т.д. неоднократное повторение этого цикла полностью уравновешивает схему.
Сходимость этого процесса (метод Некрасова) гарантирована. Столбец напряжений первой гармоники U на диодах связан с вектором уравновешивающих напряжений V в точках А, В, С матрицей взаимных проводимостей линейной электрической цепи U=AV. Столбец напряжений других гармоник на диодах равен U2=DU, (где D-диагональная матрица с положительными элементами). Столбец напряжений этих гармоник в точках А, В, С равен V2=A* U2=A* DAV. Он связан с V симметричной положительно определенной матрицей A*DA, удовлетворяющей условиям сходимости метода Некрасова.
Возможны два основных режима использования схемы.
В первом режиме роль неизвестных играют напряжения первой гармоники в точках А, В, С. Фильтр 4 и усилитель 5 настраиваются на третью гармонику. После уравновешивания схемы напряжения на диодах 1 становятся равными нулю, что обеспечивает выполнение заданных соотношений между неизвестными.
Во втором режиме заданная система уравнений посредством замены переменных yi=xi+a (где а - достаточно большее положительное число) приводится к такому виду, когда все неизвестные положительны. В этом случае роль неизвестных играют положительные постоянные напряжения (нулевая гармоника) на диодах. Фильтр 4 и усилитель 5 настраиваются на постоянную составляющую. Уравновешивающие напряжения Е1, Е2 и Е3 изменяются вплоть до обращения в нуль постоянной составляющей напряжения в точках А, В, С. В этом случае заданные уравнения отрабатываются на постоянном токе, что повышает точность работы.
Устройство для моделирования систем линейных алгебраических уравнений, содержащее резистивную линейную электрическую цепь, например матрицу проводимостей, отличающееся тем, что, с целью упрощения устройства, оно содержит источники синусоидального напряжения, соединенные через резисторы с электрической цепью в точках приложения уравновешивающих напряжений, и диоды, подключенные к электрической цепи в точки образования невязок моделируемых уравнений.
Авторы
Даты
1968-11-20—Публикация
1967-05-07—Подача