Изобретение относится к области автоматики, вычислительной и электроизмерительной техники.
Известны устройства для вычисления элементарных функций, реализующие принцип аппроксимации и построенные на нелинейных элементах. Однако у этих устройств ограниченные функциональные возможности, поскольку они пригодны для вычисления отдельных функций и не являются универсальными. К тому же при высокой сложности они не точны.
Целью изобретения является построение устройства для вычисления элементарных функций, заданных в число-импульсной форме, с высокой точностью. Для этого в нем выход устройства соединен со входом делителя частоты, управляющие входы которого соединены с выходами коммутатора коэффициентов деления, выход делителя частоты подключен ко входу реверсивного счетчика, выходы которого соединены со входами дешифратора, выходы дешифратора соединены со входами первой и второй собирательных схем и соответствующими входами коммутатора коэффициентов деления, выходы первой и второй собирательных схем соединены соответственно со входами установки «1 и установки «О триггера, выходы которого подключены к управляющим входам реверсивного счетчика.
В устройстве реализуется метод линейной аппроксимации кривых элементарных функций в дискретной форме. Количество линейных участков и их угловые коэффициенты Ki
определяются максимальной погрешностью аппроксимации вычисляемой функции (x). Оптимальные участки аппроксимации при заданной погрешности аппроксимации определяются из следующих соображений.
Пусть необходимо определить аргумент х функции y f(x), заданной в число-импульсной форме, при максимальной погрешности аппроксимации Для первого участка аппроксимации (в общем случае при , когда
) можно записать;
yi или y yo + kix,
где г/1 их - приближенные значения функции и аргумента, соответствующие первому линейному участку;
fei - угловой коэффициент этого участка.
У Уо .
--Х-Ала получим
Учитывая, что .
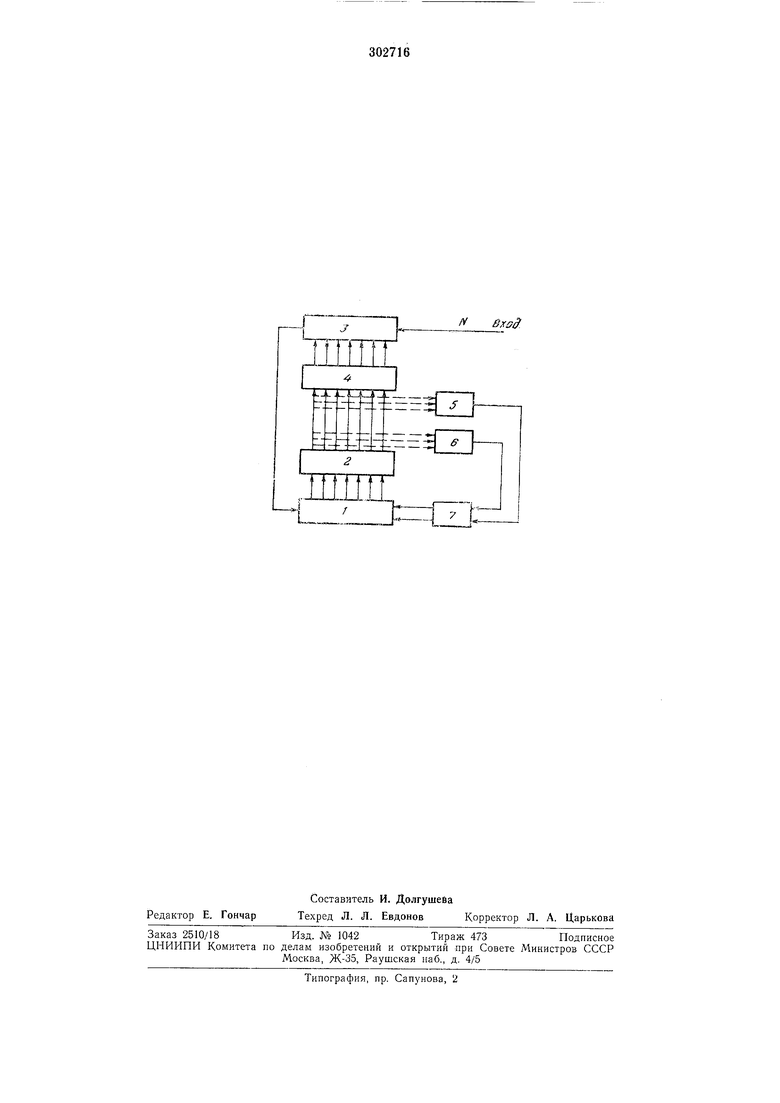
ДХо X-X. Верхняя граница первого участка аппроксимации Xi определяется из выражения; kix,f(x,}.(2) На втором участке аппроксимации (Xi.) y2 y(xi) +yo + k2(x-Xi) или 7 - V -J- () л - Л1 -t-, а погрешность аппроксимации Ах -f{x} X - --J-o-X- i) АЛЛа - / Л) Л- Значение функции , при которой погрешпость аппроксимации максимальна, определяется аналогичпо (I). Верхнюю границу второго участка аппроксимации можно найти из выражения; 2(X2-Xl)/(2)-f(l)-/(0).(4) Аналогично находятся угловые коэффициенты и границы остальных участков аппроксимации. Совершенно также определяются участки аппроксимации, если необходимо выполпить обратную задачу; по заданному аргументу вычислить соответствующее ему значение функции. В этом случае задаются максимальной погрешностью аппроксимации Аг/а гаах- В остальном выбор участков аппроксимации аналогичен предыдущему. Таким образом, при числовом задании фупкции (x) или аргумента x F(y), этот числовой эквивалент удобно сравнивать с эталонной мерой Аг/дг или Axgj, которая соответствует при линейпом приближении определенному значению аргумента А.Гд или функцип Ауд. Наиболее удобным оказалось воспроизведение эталонной меры с помощью делителя частоты (ДЧ). Величина коэффициента деления Qi ДЧ на каждом из участков определяется донустимой погрешностью дискретности Ауд или и выбирается из условия; y(xi)y() 41 Ay,, : , F(yi-F)yi-i . Ay,- (6) i ,i -Ai/, i Изменение коэффициента деления qi в узлах аппроксимации должно производиться автоматически. Вычисленное значение аргумента определяется выражением; n у - у() f-f(y;,i) / На чертеже изображена блок-схема устройства, где введены следующие обозначения; 1 - реверсивный счетчик, 2 - дешифратор, 3 - делитель частоты с переменным коэффициентом деления, 4 - коммутатор коэффициентов деления, 5 и 6 - собирательные схемы, 7 - триггер знака, задающий режим работы счетчика. Рассмотрим работу устройства при вычислении аргумента х по значению функции У (х). В исходном состоянии коэффициент деления делителя устанавливается с помощью коммутатора 4 равным qi. Число импульсов N, соответствующее заданному значению функции у, поступает на вход делителя. Каждый выходной импульс делителя соответствует определенной величине аргумента А.Хд, определяемой коэффициентом ki по формуле (5). Выходные импульсы делителя записываются в реверсивный счетчик с учетом знака углового коэффициента, который задается триггером. Нри достижении первого узла аппроксимация Xi счетчиком через дешифратор выдается сигпал на переключение коммутатора, т. е. на перестройку коэффициента деления делителя с величины qi на величину qz- В дальнейшем работа устройства повторяется. Задание режимов работы счетчика триггером производится с помощью собирательных схем, которые подключены к выходам или дешифратора, соответствующим положительным и отрицательным значениям угловых коэффициентов. При окончании процесса вычислений в счетчике будет зафиксировано искомое значение аргумента х из формулы (7). Работа устройства аналогична при вычислении функции у при заданном значении аргумента X. Нри этом для каждой элементарной функции цроизводится выбор участков аппроксимации, исходя из максимальной погрещности аппроксимации. Наиболее удобно выбор угловых коэффициентов проводить графоаналитическим методом и проверять достоверность этого выбора по формулам для максимальных погрешностей аппроксимации на каждом участке. В соответствии с полученными угловыми коэффициентами ki и требуемой дискретностью вычислений АХд или At/g по формулам (5) или (6) рассчитываются коэффициенты деления qi делителя. Эти коэффициенты задаются коммутатором по определенной программе, задаваемой дешифратором. Рассмотрим в качестве примера вычисление функции y arctg у. Для первого участка аппроксимации
Ay arctgy- f-. ki
Максимальное значение погрешность принимает при
г/to/Ai-l,
тогда
А /а1шах arCtg К, - 1 - .
kl
Верхняя граница yi первого участка апироксимации определяется из выражения:
kiyi tgyi На втором участке аппроксимации
)
(yi)+k2(y-yi), или
, + У ki
а погрешность аппроксимации
Аг/а arctgу у - У-У(
ki
Аналогично предыдущему находятся угловые коэффициенты и границы второго и следуюш,их участков аппроксимации.
Расчетные величины (в град.) оптимальных участков аппроксимации для четырех значений . приведены в таблице. (Расчеты проведены графоаналитическим методом)
Номера участков
Из таблицы видно, что погрешность аппроксимации может быть мала при небольшом количестве участков. Так, погрешность аппроксимации lAz/a max 30 МОЖНО обеспечить тремя участками аппроксимации. Угловые коэффициенты для этих участков будут иметь зна-, 0,0243
чения: 0,0185, u,, 0,0317
град.град.град.
ответственно.
При дискретности вычисления Дг/д 30 из формулы (5), учитывая 30 определяем коэффициенты деления, которые будут
иметь значения 0,0093-, 0,0122 и
град.0,5 град.
0,0159-;;-;7:;-. ПрИ ДИСКреТНОСТИ ВХОДНЫХ ИМ0,5 град, пульсов 0,0001
эти коэффициенты будут
ЦМП.
93.122 и 159
0,5 град.
Поэтому коммутатором в делителе первым устанавливается коэффициент деления 1 93.
Тогда после каждых 93 входных импульсов появляется импульс на выходе делителя, который соответствует 30. При достижении счетчиком значения у-2 появляется управляющий потенциал на одном из выходов дешифратора,
который изменяет коэффициент деления коммутатора и делает его равным . Дальше работа устройства повторяется.
Предмет изобретения
Цифровое устройство для вычисления элементарных функций, заданных в числовой форме, содержащее реверсивный счетчик, дешифратор, триггер, делитель частоты, коммутатор коэффициентов деления и собирательные схемы, отличающееся тем, что, с целью расширения функциональных возможностей и повышения точности в нем выход устройства соединен со входом делителя частоты, управляющие входы которого соединены с выходами коммутатора коэффициентов деления, выход делителя частоты подключен ко входу реверсивного счетчика, выходы которого соединены со входами дешифратора, выходы дешифратора соединены со входами первой и второй собирательных схем и соответствующими входами коммутатора коэффициентов деления, выходы первой и второй собирательных схем соединены соответственно со входами установки «1 и установки «О триггера, выходы которого подключены к управляющим входам реверсивного счетчика.
„ШЛ1
I-J/
1 Bxsl


| название | год | авторы | номер документа |
|---|---|---|---|
| ЦИФРОВОЙ ФАЗОМЕТР | 1973 |
|
SU385236A1 |
| Устройство для вычисления функций вида у=ах @ и у= @ | 1980 |
|
SU885998A1 |
| Функциональный преобразователь двух переменных | 1984 |
|
SU1168964A1 |
| Устройство для вычисления функций у=тGх и у=стGх | 1980 |
|
SU935950A1 |
| Устройство для вычисления функций у=aRcSINx и у=aRccoSx | 1980 |
|
SU935949A1 |
| Устройство для вычисления функции | 1977 |
|
SU734710A1 |
| Устройство для вычисления функций | 1977 |
|
SU736115A1 |
| Устройство для отображения графической информации на экране электронно-лучевой трубки | 1980 |
|
SU879635A1 |
| Устройство для вычисления функции арктангенса отношения | 1990 |
|
SU1751750A1 |
| Функциональный преобразователь | 1983 |
|
SU1115069A1 |


Авторы
Даты
1971-01-01—Публикация