Предлагаемое устройство принадлежит к числу известных вообще устройств, в которых решение уравнений получается путем соответственного подбора элементов электрической цепи и измерения возникающих при этом сопротивлений, напряжений или сил токов.
В частности, устройство имеет целью решение алгебраических простых и трансцедентных (тригонометрических) уравнений высших степеней путем сравнения сил электрических токов, протекающих по определенным образом подобранным сопротивлениям.
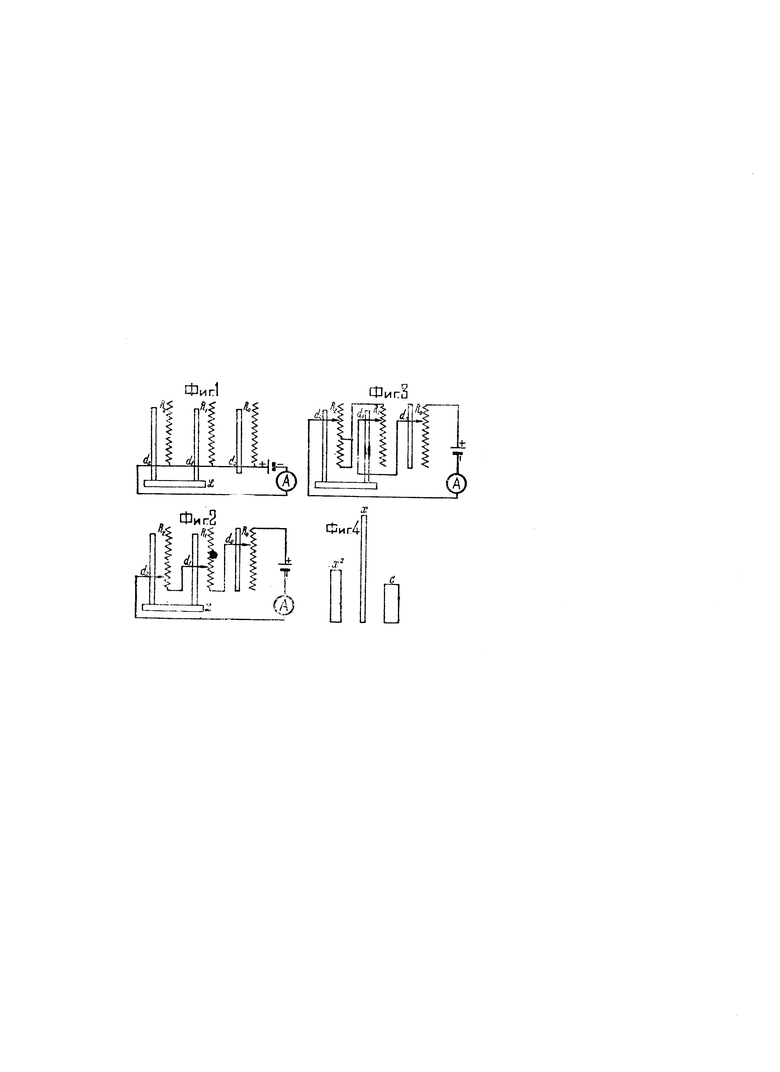
Мысль, лежащая в основе изобретения такова: возьмем электрическую цепь постоянного тока с каким-то начальным сопротивлением, величина которого не имеет особого значения. Пусть к этой цени приложено какое-то постоянное же напряжение Е, в ней установится ток 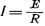 . Теперь включим в эту цепь сопротивление, равное в каких-либо условных единицах свободному числу решаемого уравнения или же, если этот член отрицателен, выключим соответственной величины сопротивление. Сила тока изменится. Чтобы она стала прежней, необходимо сопротивление цепи изменить на величину, равную свободному члену, но обратную ему по знаку. Воспользуемся этим для решения уравнений. С этой целью построим прибор, составленный так (см. фиг. 1, общий вид прибора). Прибор заключает в себе столько реостатов сопротивления, сколько членов может быть в решаемом уравнении. Один из этих реостатов обозначим R0. Этот реостат соответствует свободному члену и снабжен шкалой, вдоль которой может передвигаться контакт d0. Мы можем установить на этом реостате сопротивление, равное (в каких угодно единицах) свободному члену. Остальные реостаты обозначим R1, R2, R3 … и т.д., выбивая индекс в соответствии с тем, что они назначены для изображения членов с неизвестным в первой, второй, третьей степени и т.д. Эти реостаты также снабжены шкалами и передвижными вдоль шкал движками-контактами d1, d2, d3 …. Но шкалы всех этих реостатов логарифмические, причем равные отрезки на шкалах сопротивлений R1, R2, R3 и т.д. дают (подобно квадратной и кубической шкалам на логарифмической линейке) квадраты, кубы и т.д. Сопротивления на реостатах же намотаны так, чтобы в тех же единицах сопротивления, в которых градуирована шкала R0, они давали, при соответственных установках движков, сопротивления, равные отметкам, нанесенным на шкалы. Как пример выполнения мы имеем реостат, изображенный на фиг. 4. В нем площадь сечения шаблона обмотки одна и та же, что сохраняется посредством изменения ширины при разных высотах (длинах).
. Теперь включим в эту цепь сопротивление, равное в каких-либо условных единицах свободному числу решаемого уравнения или же, если этот член отрицателен, выключим соответственной величины сопротивление. Сила тока изменится. Чтобы она стала прежней, необходимо сопротивление цепи изменить на величину, равную свободному члену, но обратную ему по знаку. Воспользуемся этим для решения уравнений. С этой целью построим прибор, составленный так (см. фиг. 1, общий вид прибора). Прибор заключает в себе столько реостатов сопротивления, сколько членов может быть в решаемом уравнении. Один из этих реостатов обозначим R0. Этот реостат соответствует свободному члену и снабжен шкалой, вдоль которой может передвигаться контакт d0. Мы можем установить на этом реостате сопротивление, равное (в каких угодно единицах) свободному члену. Остальные реостаты обозначим R1, R2, R3 … и т.д., выбивая индекс в соответствии с тем, что они назначены для изображения членов с неизвестным в первой, второй, третьей степени и т.д. Эти реостаты также снабжены шкалами и передвижными вдоль шкал движками-контактами d1, d2, d3 …. Но шкалы всех этих реостатов логарифмические, причем равные отрезки на шкалах сопротивлений R1, R2, R3 и т.д. дают (подобно квадратной и кубической шкалам на логарифмической линейке) квадраты, кубы и т.д. Сопротивления на реостатах же намотаны так, чтобы в тех же единицах сопротивления, в которых градуирована шкала R0, они давали, при соответственных установках движков, сопротивления, равные отметкам, нанесенным на шкалы. Как пример выполнения мы имеем реостат, изображенный на фиг. 4. В нем площадь сечения шаблона обмотки одна и та же, что сохраняется посредством изменения ширины при разных высотах (длинах).
Как один из возможных примеров практического выполнения предлагаемого устройства и способа расчета его можем указать следующее. Выберем в качестве произвольных исходных расчетных размеров реостата длину 250 мм и ширину 10 мм и будем деления и расчеты нашего реостата вести в соответствии с делениями обычной логарифмической линейки, имеющей шкалу длиной также в 250 мм. Разделим длину реостата, в соответствии с девятью делениями логарифмической линейки, на 9 равных частей; каждая из них будет равна 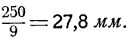 Площадь любого из указанных 9 делений равна 27,8×10=278 мм2. Обозначим эту площадь через с, длина же деления на логарифмической линейке, простирающегося от 1 до 2, будет при указанном типе равна 75,26 мм. Обозначим эту длину через х. Эту длину должно иметь первое деление на реостате, соответствующем первым степеням. На реостате, соответствующем квадратам, полная шкала от 1 до 9 будет вдвое меньше, т.е. 125 мм и длина деления 1-2 получится равной 37,63 мм. Обозначим ее через x2. Для того, чтобы получить на логарифмических шкалах площади той же величины, что на шкале, соответствующей свободному члену, мы должны изменить ширину реостата в той пропорции, в какой длина деления шкалы для данного реостата отличается от того же деления шкалы на реостате свободного члена. В нашем случае ширина реостата для деления 1-2 получится на реостате, соответствующем первым степеням, равной
Площадь любого из указанных 9 делений равна 27,8×10=278 мм2. Обозначим эту площадь через с, длина же деления на логарифмической линейке, простирающегося от 1 до 2, будет при указанном типе равна 75,26 мм. Обозначим эту длину через х. Эту длину должно иметь первое деление на реостате, соответствующем первым степеням. На реостате, соответствующем квадратам, полная шкала от 1 до 9 будет вдвое меньше, т.е. 125 мм и длина деления 1-2 получится равной 37,63 мм. Обозначим ее через x2. Для того, чтобы получить на логарифмических шкалах площади той же величины, что на шкале, соответствующей свободному члену, мы должны изменить ширину реостата в той пропорции, в какой длина деления шкалы для данного реостата отличается от того же деления шкалы на реостате свободного члена. В нашем случае ширина реостата для деления 1-2 получится на реостате, соответствующем первым степеням, равной 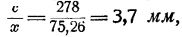 мм, а на реостате, соответствующем квадратам, она будет равной
мм, а на реостате, соответствующем квадратам, она будет равной 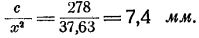 мм. Таким же образом можно вычислить эквиваленты ширины для остальных делений шкал реостатов, и, в частности, как для более крупных, так и для более мелких делений.
мм. Таким же образом можно вычислить эквиваленты ширины для остальных делений шкал реостатов, и, в частности, как для более крупных, так и для более мелких делений.
Реостат, соответствующий свободному члену, может иметь произвольную форму сечения и длину при условии, что сопротивление его во всех единицах шкалы будет равновелико с соответствующими сопротивлениями шкалы первых степеней. Естественно, что наиболее целесообразно реостаты свободного члена и первой степени выполнить одинаковыми. Все эти сопротивления расположены рядом, параллельно друг другу, а передвижные контакты d1, d2, d3 и т.д. их могут быть взаимно сцеплены посредством общей подвижной линейки L так, чтобы все они одновременно перемещались вдоль этих реостатов на одну и ту же линейную величину. Тогда, в том случае, если они переместились так, что сопротивления на реостате R1 изменится на а единиц, то на реостате R2 оно изменится на a2 единиц, на реостате R3 - на a3 единиц и т.д. Устроим, кроме того, контакты d1 d2 d3 … так, чтобы их можно было перемещать не только сразу все вместе, но и порознь, а затем вновь сцеплять вместе в любом положении. Это позволит, приступая к решению уравнения, на каждом из реостатов установить сначала каждый подвижной контакт на делении, равном численному значению коэфициента при соответствующем члене уравнения, а затем сцепить все их механически вместе на линейке L. Сами же реостаты должны быть включены в электрическую цепь так, чтобы сопротивления тех из них, которые соответствуют положительным членам, возрастали при перемещении линейки L от ее начального, так сказать, нулевого положения. Реостаты же, соответствующие отрицательным членам уравнения, должны быть соединены обратно, т.е. их сопротивление должно падать при том же перемещении линейки L. Ясно, что в этих условиях перемещения, каждое положение линейки L соответствует помножению коэфициентов уравнения на соответственные степени одного и того же числа. Когда число равно корню уравнения, то суммарное сопротивление, набранное на реостатах R1, R2 …, равно свободному члену, т.е. сопротивлению на реостате R0 и при правильном включении может уравновесить цепь согласно Rобщее=R1+R2+R3 …, т.е. приведет ее к начальному значению сопротивления. Этим уравнение будет решено и значение корня прочтем на масштабе шкалы R1, так как алгебраическая сумма всех геометрических отрезков, выражающих каждый член уравнения, равного нулю, тоже равна нулю. Таким образом манипулирование с прибором сводится к следующему. Пусть мы имеем уравнение х2+2х-8=0. Для разыскания положительных корней делаем подстановку x=+x; получаем х2+2х-8=0. Соединяем (фиг. 2) начальный конец реостата R2 с контактом d1, начальный конец реостата R1 с контактом d2, конец реостата R0 с батареей, амперметром А и контактом d2. Ставим контакты d0, d1, d2 на начальные значения соответствующих им реостатов R0, R1, R2, получаем замкнутую цепь тока с показанием I амперметра А, соответствующим какому-то сопротивлению R всей цепи. Закрепляем контакты: d0 - на делении 8, d1 - на делении 2, d2 - на делении 1 и двигаем линейку L до тех пор, пока не получим прежнего показания I амперметра А. Сопротивления R2, R1 будут увеличиваться при передвижении линейки L, а общее сопротивление R цепи будет уменьшаться на величину R0.
При достижении указанной силы I тока мы прочтем на шкале реостата R1 против контакта d1 деление 4, а против начального деления шкалы, на которой закреплен контакт d1 деление 2, что и будет положительным корнем уравнения. Для разыскания же отрицательных корней данного уравнения x2+2x-8=0 делаем подстановку x=-x, получаем x2-2x-8=0. Соединяем (фиг. 3) начальный конец реостата R2 с концом реостата R1, а контакт d1 с контактом d0, конец реостата R0 с батареей, амперметром А и контактом d2. Установив контакты d2, d1, d0 на начальные значения шкал соответствующих им реостатов R2, R1, R0, получаем замкнутую цепь тока с показанием I′ амперметра А, соответствующим какому-то новому сопротивлению цепи R′. Закрепляем контакт d2 на делении 1, контакт d1, на делении 2, контакт d0 на делении 3 и подвигаем линейку L до получения прежнего показания I′ амперметра А. Теперь сопротивление R2 будет увеличиваться, а сопротивление R1 будет уменьшаться при движении линейки L, общее же сопротивление R′ всей цепи будет уменьшено на величины R′0. При силе I′ тока прочтем на шкале реостата R1 против контакта d1 деление 8, а против начального значения шкалы, на которой закреплен контакт d1; деление 4, что и будет отрицательным корнем данного уравнения.
Для ясности на фиг. 2 и 3 линейка L не подвинута, как должно было бы быть, а лишь показано приблизительное нахождение контактов d2, d1, d0 на реостатах R2, R1, R0. Также на фиг. 1, 2, 3 не показано у реостата R2, что вторая часть сопротивления, как должно быть, больше первой части этого же сопротивления в 10 раз.
Естественно, что таким образом мы можем построить подобные устройства для решения уравнений в любой степени, выраженной целым числом и, манипулируя вышеуказанным способом, получить его рациональные корни.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ АВТОМАТИЧЕСКОГО ПРОИЗВОДСТВА ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ | 1932 |
|
SU36063A1 |
| УСТРОЙСТВО ДЛЯ ДУПЛЕКСНОЙ РАДИОТЕЛЕГРАФИИ И РАДИОТЕЛЕФОНИИ | 1925 |
|
SU3515A1 |
| СПОСОБ ГЕНЕРАЦИИ РАВНОМЕРНО РАСПРЕДЕЛЕННЫХ И НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ЧИСЕЛ | 2013 |
|
RU2583729C2 |
| СПОСОБ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ | 1998 |
|
RU2137144C1 |
| ПРИБОР ДЛЯ ЭКСПЕРИМЕНТАЛЬНОЙ ПРОВЕРКИ ЗАКОНА АМПЕРА | 2006 |
|
RU2321074C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ТРАЕКТОРИИ ПЕРЕВОДА СУДНА НА ПАРАЛЛЕЛЬНЫЙ КУРС С СОБЛЮДЕНИЕМ ОГРАНИЧЕНИЙ НА ДИАПАЗОН ИЗМЕНЕНИЯ СИГНАЛА УПРАВЛЕНИЯ | 2012 |
|
RU2515006C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРИЕНТАЦИИ ОБЪЕКТОВ В ПРОСТРАНСТВЕ, ДАЛЬНОСТИ, ПЕЛЕНГА, КООРДИНАТ МЕСТОПОЛОЖЕНИЯ И СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ ПО НАВИГАЦИОННЫМ РАДИОСИГНАЛАМ КОСМИЧЕСКИХ АППАРАТОВ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ | 1998 |
|
RU2152625C1 |
| Способ получения экстракта из растительного сырья куркумы с повышенным содержанием куркумина | 2020 |
|
RU2762903C1 |
| ВОСПРИЯТИЕ ВЫСОКОТЕМПЕРАТУРНОГО ДАВЛЕНИЯ | 2015 |
|
RU2668945C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЯ ДЕФОРМАТИВНОСТИ МАТЕРИАЛА | 2004 |
|
RU2276779C1 |
1. Электрическое устройство для решения алгебраических уравнений высших степеней с одним неизвестным, в котором решение определяется методом достижения электрической цепью определенного равновесного состояния, отличающееся тем, что оно состоит из набора реостатов в числе, равном числу членов решаемого уравнения или большем его, из каковых реостатов один, назначенный для изображения свободного члена, выполнен произвольным образом, а остальные реостаты выполнены так, что все они имеют равную длину, величины сопротивления реостатов, изображающих различные степени неизвестного, относятся друг к другу, как первая степень, квадраты, кубы и т.д., причем сопротивление нанесено на реостаты так, чтобы отрезки реостата, соответствующие первой степени, были пропорциональны по длине логарифмам изображаемых чисел, на равных же отрезках реостата, соответствующего второй степени, откладывались сопротивления, равные квадратам тех же изображаемых чисел и т.д. на остальных реостатах.
2. В устройстве по п. 1 применение приспособления, позволяющего одновременное перемещение на равные линейные отрезки всех передвижных контактов реостатов, соответствующих членам, заключающим неизвестное.
3. В устройстве по пп. 1 и 2 применение приспособления, допускающего предварительное установление подвижных контактов реостатов на величины, соответствующие коэфициентам при различных степенях неизвестного, а затем закрепление этих контактов с целью одновременного перемещения их.
4. В устройстве по п. 1 применение, в качестве шаблона для намотки реостатов, шаблонов равной длины, но таких сечений, переменных по длине, чтобы длина провода, наматываемого на реостат, могла составить сопротивление, меняющееся так, что отрезки реостатов, соответствующие определенным числам, имеют длину, пропорциональную логарифмам этих чисел.
Авторы
Даты
1934-08-31—Публикация
1931-07-14—Подача