(54) УСТРОЙСТВО ОПРЕДЕЛЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для ортогонального преобразования сигналов | 1976 |
|
SU653756A1 |
| Устройство коррекции выходных сигналов | 1989 |
|
SU1705768A1 |
| УСТРОЙСТВО ДЛЯ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ИНФОРМАЦИИ | 1972 |
|
SU357565A1 |
| Устройство для фильтрации симметричных составляющих | 1985 |
|
SU1343362A1 |
| Устройство для цифровой обработки сигналов | 1985 |
|
SU1336028A1 |
| Устройство для вычисления корреляционной функции | 1987 |
|
SU1472916A2 |
| Цифровой фильтр с многоуровневой дельта-модуляцией | 1988 |
|
SU1587624A1 |
| Устройство для решения задач планирования экспериментов | 1984 |
|
SU1317450A1 |
| Устройство для спектрального анализа | 1981 |
|
SU1013972A1 |
| Прогнозатор постепенных отказов | 1982 |
|
SU1053113A1 |


.1
Изобретение относится к области вы числительной техники и может быть использовано в цифровых управляющих вычисли; тельных машинах различного назначения, в частности в устройствах, осуществляющих -ци4ровую обработку-радио/юкационной информации.
Известно ци(овое устройство, сглажива ваюшее случайную погрешность, наложенную на квадратичную функцию. Оно состоит .из запоминающего устройства, блоков вычисления весовых коэффициентов, блоков .; умножения и сумматоров.
Алгоритм операции сглаживания, используемый в известном устройстве, тре- бует выполнения большого количества операций.
Цель изобретения - упрощение устройства.
Это достигается тем, что предлагаемое устройство содержит блоки формирования сигналов, причем выход блока памяти под- ключен к входам первого и второго блоков формирования сигналов, выходы которых . соединены с первыми входами второго и I
i третьего блоков умножения соответственно, вторые входы которых подключены соот ветственно к выходам третьего и четвертого блоков формирования сигналов.
Выводим алгоритм сглаживания, исполх зуемый в изобретении.
Обозначим бремя последнего измерения JJjP О, время предьщущего измерения - i
ir TC) + и время последнего
.используемого измерения V. Результат последнего измерения принимаем за у, предыдущего - за .... У/
На инте1рвале сглаживания с П-i ДЛИ-. нцй выделяем три отрезка длиной с ffl-:f) определяем среднее
значение несглажеиной функции на каждом i отрезке VL.Tw V 5 )
Чр п-1 f Yi; .i: ч; t-0 , f; ;: ццп-«
; -.4.-/ i Через точки с коорйинатами;, I -. ., ) 2cf -i . 0|(n 10 5ср ; i д 4 проводим 2. : квaдpaти шyю параболу Y Ь + bjt и определяем коэффициенты 6 л. ) т . 2ср, u «, 4. «. + V 1 ,t3,,t3cp Y3cp-J Учитывая, что t,p 0,l(n-0ut, ,5Cn-l)At И 1з,р.0,9(п-0д1, находим главный определитель системы т 16 , v3 .5 D ioFlti-i) д1 . Для отыскания коэффициента Ьо нахо дим определитель 2 .0,2tn-l)(ПН)пм ,Х Y;-2.2: Yi-J-.H УЛ t-01 о,Шм) .0,8Сп-1) гда Да, 15,63 ,}2(п-1) о,е(п-1) br -i-jTJi .ь ., . Дх Ц Y )чО) , , . -. i Для отыскания коэффициента v/ вычис : ляем определитель лqiltl- lOfitn- l A. tn-l)At4-2,8 Г Y,+4r Z YI i 01--ОЛ(пм) 0-J -i.), 1-огда. , A/1,(J2(n-1) V-pT IFTiSTT -2 -88 S n, (4 ,e(n:ilfi-1 -3,a5. ,38.2: Y; ). - Q Ctl-l),8(n-l) КоэффицИенты , принимаем за математические ожидания двух старших
451999
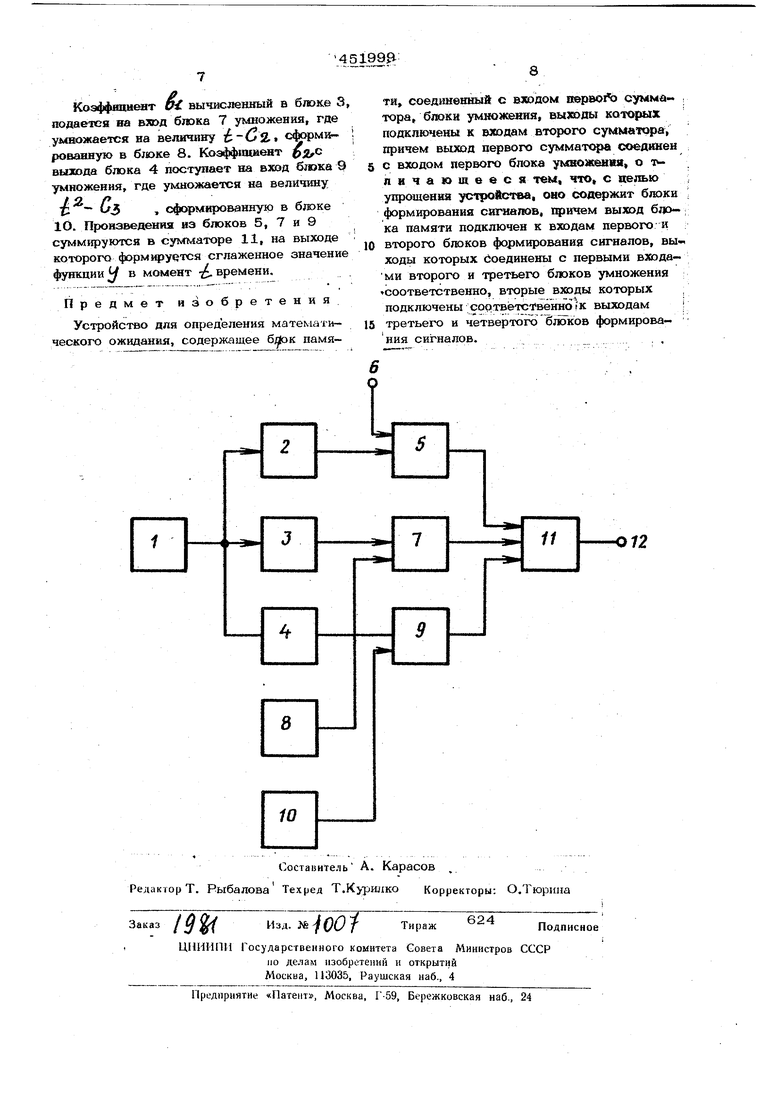
4 коэффициентов сгпаживающего полинома. Вычисляем/-е значение нулевого коэффиниента, / boj Yj-b,jut-b2Cjut) На интервале сглаживания выбираем отрезокJ / .л/ и определяем эмпири., ческое математачёско ё ожидание коэффици ент 023(tl-l) 1.0Г 1Гм jj Yi.. д1-bgi fltj 4. Qi5(n-i) b1лt cjism-i) «ег-%. n-1 JQ i ПМ УО bzAi l. ilb Читывая, что ) . ,o )()t) & о,2б(, +3 Ь - Y- X ) ° .о,25(п-1}o,s(ftM)R-1 «(21,885: --31,252: Yj. 9,38 Z YjV ,8(n-i) .. ) 0t OAinn) . -0,8() Найденную величину принимаем за нупецо& коэффициент сглаживающего полинома, тогда o,) Y,Jt)-c,Z Y-b,Ct-c,).b,Ct4,), (6) Де Г - JL r )ut a- 8 (3)(ntl}ut C::J g«« Определяем количество операции, необходимое для выполнения операции сглаживания по |алгоритму (6). На начальном, участке формирование суммы 4- Д5{п-) требует вьшо ния операций сложения и одн операции умножения; вычисление коэфф ента трех операций умножения и - { 1-1К2 5 операций слож вычисление коэффициента g, - одной o рации умножения и двух операций слож В целО1чг сглаживание на начальном уч ке потребует .Hau ,. При ВЫ) ю ли ей и и V :) шаг сглажиБа11Ий огысканне суксл o,Z5(fi-i) 42{п-4) о,6{п-1)п-1 21 П ; 2: V-, И Yi , Z UOi rOr-OM -) ,8(nосуществляем с использовсЗнием этих ж величин, найденных в предыдущем /С-шаге сглаживания, 0,25(НМ) 0,)+1 .Z Y X Y;-Y«.. Y o,ztn-i)-i o,2(n-i) Г L .2: V,-Y.,-Y 0 ) 0,6 (n-i) абсп-1}м ,4(11-1) Uo,4(n-iVi ,6(n-iVi o,f V, - , Y чу ,8tn-i) i.0,ain-.)/i- o,Blti-ii ) ™eo,a5(n-.)., ,,,,..,, Ci4(n-lVl t 0,6ttl-1)H величины, на.-гдониые при -вьтолнении п дыдущего шага сглаживания. Тогда тек Щий шаг сглажииания требует оптек - м . Следовательно предлагаемое устройств сглаживания требует всего семь множ тельных и шестнадцать суммирующих ройств, т. е. оказывае1х;я проще извес го в 2О-30 раз или иметь производит ность в 2О-30 раз большую. Сравним среднеквадраттные ошибки о сглаживания функции известного и пре гаемого устройств. Среднеквадратичная погрешность известного усаройства онре- , деляется выражением j 3 Ана-. п iR Y ЛИЗ обычными способами показывает, что среднеквадратичная погрешность предлагаемого устройства составляет ) Таким образом, среднеквадратичные ошибки Qyn, известного и предлагаемого уст ройств достаточно близки. На чертеже показана блок-схема устройства для определения математического ожидания квадратичной параболы. Устройство состоит из блока 1 памяти, выход которого соедиТнен с входом сумматора 2, и блоков 3, 4. Выход сумматора связан с входом блока 5 умножения, второй вход 6 которого подключен к постоянному запоминающему устройству. Выход блока 3 соединен с входом блока 7 умножения, второй вход KOTOpoix) связан с выходом блока 8. Выход блока 4 подключен к входу б;юка 9 умножения, второй вход которого соединен с выходом б;юка 10. Выходы блоков 5, 7 и 9 соединены с входами суммаюра 11, выход 12 которого является выходом устройства. Устройство работает следующим образом. Результаты измерений сглаживаемой функции поступают в блок 1 памяти, KOIXJрый хранит результаты /Z- последних измерений У),у, Jll-{ С выхода блока памяти значения несглаженной функции подаются на входы сумматора 2 и блоков 3, 4. В сумматоре формируе1х;я сумма агб{п-О Z прямым суммированием на начальном участке и по алгоритму (8) на текущем участке. В блоке 3 ({юрмируется коз4)фициент по алгоритму (4), причем вычисление сумм чг(п-1) ) fi-1 Z -L. .X Y , ,Z Yi , L-0L-0,f(n-l)t-0 111-1) ствляетсп прямым суммированием на начальном участке и по алгоритмам (9), (1О), (11) на текущем участке. В блоке 4 вычисляется коэффициент по алгоритму (3). В блоках 8, 1О формируютс я разности . ( i - {; z соогветс/твенно. Величина,f- ij г,, мулированная в сумматоре 2,° юстуиает на вход блока 5 умножения, где умножается на коэффициент - поступающий на вход блока 8.
Коэффвянент v. вычисленный в блоке 8, подается на вяод блока 7 умножения, где умножается на величину . сформ рованную в б;юке 8. Коэффшшент выхода блока 4 поступает на вход б1юка 9 ножения, где умножается на величину
IP С/З , сформ1ч ованную в блоке 1О. Произведения из блоков 5, 7 и 9 суммируются в сумматоре 11, на выходе которого формируется сглаженное значение функции Ч в момент - времени,
Предмет изобретения
Устройство для определения математического ожидания, содержащее бйок памяти соединенный с входом перво1 Ь сумма тора, блоки умножения, выходы которых подключены к входам второго сумматора, причем выж)д первого сумматора соеД|Шен
S с входом первого блока умвоженвя, отличающееся тем, что с аселью упрощения устройства, оно содержит б1юки формирования сигнапов, причем выход бдо ка памяти подключен к входам первого и
10 второго блоков формирования сигналов, выходы которых Соединены с первыми входа- ми второго и третьего блоков умножения соответственно, вторые входы которых подключены соответственно к выходам
15 третьего и четвертого блоков формирования сигналов.
aJ П
Авторы
Даты
1974-11-30—Публикация
1973-02-05—Подача