в дчислительных блоков третьего столбца fi матрицы соединены с входами и выходами li процессора непосредственно.
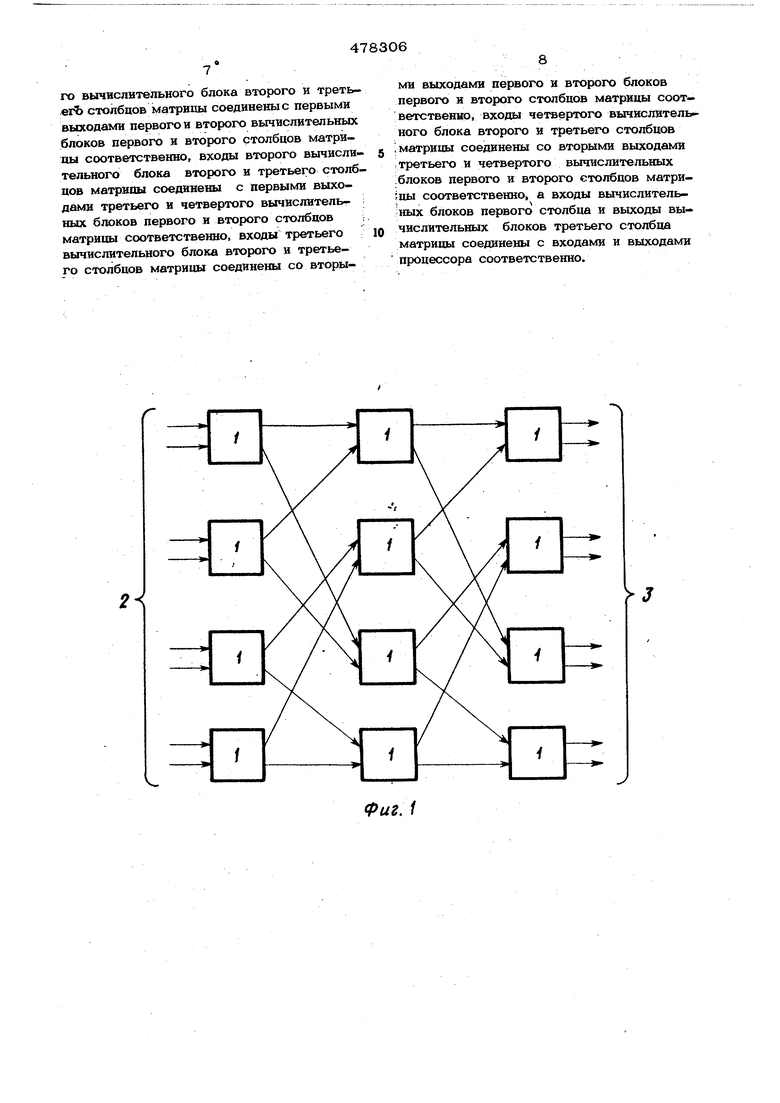
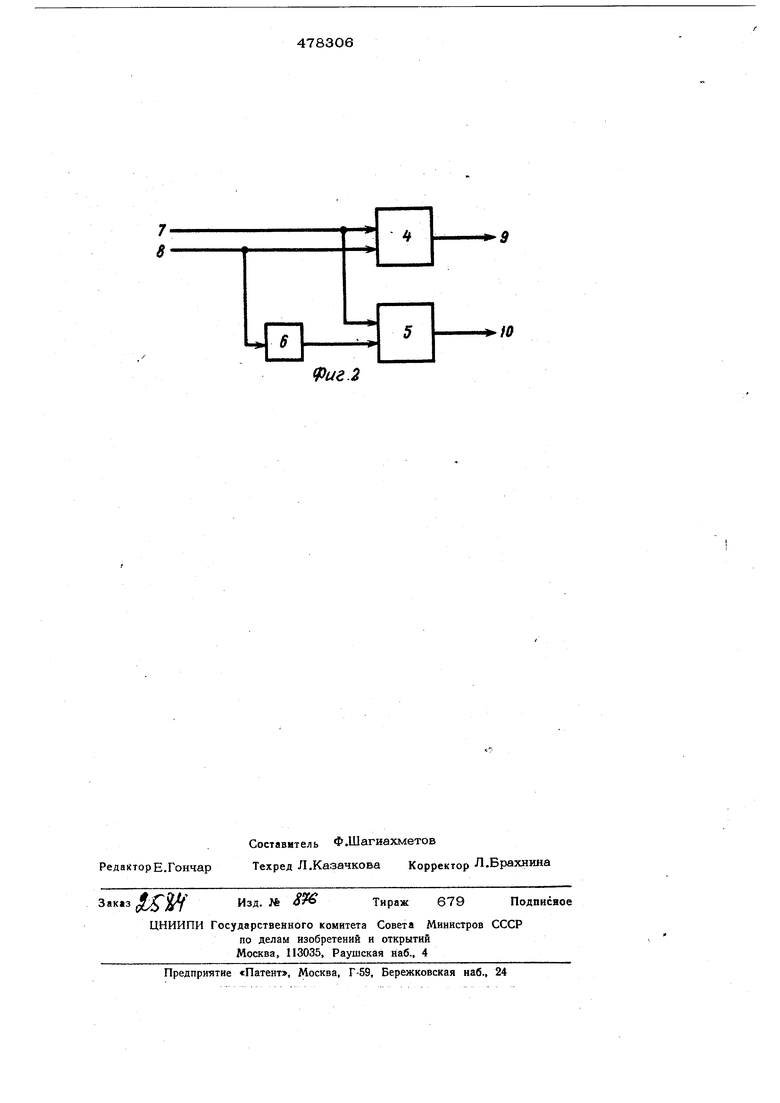
Г На фиг. 1 представлена блок-схема процессора, на фиг. 2 - схема вычисли;тельного блока.
Матричный пара 1лельный процессор со держит вычислительные блоки 1, объеди«ненные в три столбца. Цифрами 2 и 3 обозначены соответственно входы и выходы процессора.
Вычислительный блок 1 содержит сумма торы 4, 5 и инвертор 6. Цифрами 7,8 и 19, 10 рбозначены входы и выходы вычислительного блока соответственно. Информация поступает в процессор, закодированной в степенных при
; ,.- . ; -.... ,- .
:рашений (СП). Кодирование производят по следующему алгоритму:
Масштабирование информации в пределах от О до 1.
Сложение с числом 0,5. Умножение на 2. Сложение с числом 0,5.
Первые Д1ва двоичных разряда, стоящие | |слева от запятой являются очередным сте-1 :;пенным приращением..;
|| В табл. 1 приведен пример кодирования , числа ,ОО10011 в виде степенных при|ращений, тогда В (А + О,5) Г
iX.X и
1 (O.lOlOOll) где В - кодируемое
-,.
: число, at- номер шага кодирования.
Таблица 1.


| название | год | авторы | номер документа |
|---|---|---|---|
| Матричное вычислительное устройство | 1978 |
|
SU750485A1 |
| Матричное вычислительное устройство | 1990 |
|
SU1833890A1 |
| Матричное устройство для решения уравнений в частных производных | 1985 |
|
SU1302276A1 |
| Матричное вычислительное устройство | 1979 |
|
SU809174A1 |
| Делительное устройство | 1979 |
|
SU781810A1 |
| Многоканальный цифровой коррелятор | 1974 |
|
SU478315A1 |
| Множительное устройство | 1979 |
|
SU781809A1 |
| ЯЧЕЙКА ОДНОРОДНОЙ ВЫЧИСЛИТЕЛЬНОЙ СРЕДЫ, ОДНОРОДНАЯ ВЫЧИСЛИТЕЛЬНАЯ СРЕДА И УСТРОЙСТВО ДЛЯ КОНВЕЙЕРНЫХ ВЫЧИСЛЕНИЙ СУММЫ м n-РАЗРЯДНЫХ ЧИСЕЛ | 2011 |
|
RU2475815C1 |
| Матричный параллельный процессор | 1984 |
|
SU1233169A1 |
| Матричный умножитель по модулю чисел Ферма | 1990 |
|
SU1783513A1 |

В
2В
Декодирование представляет собой алJ гебраическое сложение количественных I эквивалентов (весов) степенных приращений (см. последнийч; столбец табл. 1).
Как видим,выполнение операции сложэ4« ння возможно только при отсутствии пере. носов на один разряд вперед, т. е. при отсутствии комбинаций степенных прираще|ний вида 10.1О и ОО.ОО. Это условие вы;полняется всегда в силу существования ряда теорем.
Пример сложения закодированного ранее числа А О.О010011 (СП О1.1О.ОО.
01;flO.00.10.OO.lO.ll) приведен
(СП в табл. 2.
2В + О,5
СП
Таблица 2.
Сложение производится по мере поступления приращений , в приведенном примересверху вниз, т. е. от старших приращений к младшим. Каждый вычислительный блок 1 матрич ного параллельного процессора реализует выражения: (1) Bi4..-B, (2) где i - номер столбца матричного парал лельного процессора, А,В--операнды, поступаюише на входы 7 и 8 вычислительного блока 1 соответственно. А:+1,В.+ 1 - результаты вычислений, поступающие на выходы 9 и 10 вычислительного блока 1 .матричного параллельно го процессора соответственно. Вычислительные блоки 1 соединены меж ду собой в соответствии с графом, описыи вающим быстрое преобразование Адамара. Количество входов матричного параллельного процессора всегда кратно степени двойки. Тогда количество столбцов процессора будет равно величине показателя степени, а число строк - числу входов , деленному пополам. Каждый вычисли тельный блок 1 обрабатывает информацию последовательна, начиная со старших разрядов. Вычислительный блок 1 реализует формулы (1) и (2), причем сумматор 4формулу(1), а сумматор 5 - формулу (2). Инвертор 6 необходим для умножения числа ,.лВ на -1. Работа матричного параллельного про.цессора происходит следующим образом. На входы 2 поступает последовательно информация, закодированная в виде степенных при ращений. Обработанные в первом столбце матричного параллельного процессора старщие разряды результата поступают для дальнейщей обработки во второй столбец, оттуда - в третий и т. д. В то время, как с выходов 3 происходит вьщача старщих разрядов окончательного результата преобразования Адамара, на входы 2 еще продолжают поступать младшие разряды исход ного массива чисел. Приняв с выходов 3 достаточное для обеспечения необходимой точности количество старших разр5щов результата, процесс вычислений можно остановить. Легко видеть, что работа вычислительного блока 1 матричного параллельной го процессора заключается в приеме очередных степенных приращений операндов и сложении (вычитании) их в соответствии |с формулами (1) и (2). Степенные приращения результата выдаются из вычислительшто блока 1, а на вход одновремен- yio с выдачей поступают следующие пары приращений. Следует отметить, что каждый сумматор, входящий в состав блока 1 матричного параллельного процессора, задерживает информацию-на один такт, что сдедует из указанного выше алгоритма сложения двух чисел, представленных в виде степенюлх приращений.Очевидно, что вычислительный блок 1 матричного параллельного процессора в целом также задерживает информацию на один такт. Оценим быстродействие матричного па|раллельного процессора. Оно определяется задержкой всех вычислительных блоков 1, : т. е. задержкой в наиболее короткой последовательной цепи, составленной из вычнч слительных блоков 1. В данном случае длина цепи равна количеству столбцов мат-, ричного параллельного процессора, которое можно вычислить по формуле , Тогда время, необзсрдимое для обработки всего исходного массива,чяеел (в тактах) T to9.,, где Н - количество входов матричного параллельного процессора, равное количеству чисел в исходном об- . рабатываемом массиве, а М - j число старщих разрядов результата, „; обеспечивающее необходимую точность вын числений. Если Н 1024, длительность одного такта равна 1 мксек, а М 1О, то мксек, что в 800 раз быстрее, чем у известного процессора. Предмет изобретения Матричный параллельный процессор для вычисления преобразования Адамара, со.держащий в узлах матрицы вычислительные блоки, выполненные в виде сумматорой, входы каждого из которых соединены с входами вычислительного блока, а первый выход каждого вычислительного блока соединен с выходом соответствующего сумматора, отличающийся тем, что, с целью повышения быстродействия, каждый вычислительный блок содержит инвертор и дополнительный сумматор, выход Которого соединен со вторым выходом вычислительного блока, один вход которого соединен с первым входом дополнительного сумматора непосредственно, а другой вход через инвертор соединен со вторым входом дополнительного сумматора, причем входы первого вычислительного блока второго и треть- егЬ столбцов матрицы соединены с первыми выходами первого и второго вычислительных блоков первого и второго столбцов матрицы соответственно, входы второго вычислительного блока второго и третьего столбцов матрицы соединены с первыми выходами третьего и четвертого вычислитель I ных блоков первого н второго столбцов ;. матрицы соответственно, входы третьего вычислительного блока второго и третьего столбцов матрицы соединены со вторыми выходами первого и второго блоков первого и второго столбцов матрицы соответственно, входы четвертого вычислителыного блока второго и третьего столбцов матрицы соединены со вторыми выходами : третьего и четвертого вычислительных .блоков первого и второго столбцов матри;цы соответственно, а входы вычислительных блоков первого столбца и выходы вычислительных блоков третьего столбца матрицы соединены с входами и выходами процессора соответственно.
2
х
7- 8
Фиг.2
10
Авторы
Даты
1975-07-25—Публикация
1973-07-25—Подача