(54) МАТРИЧНОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО


| название | год | авторы | номер документа |
|---|---|---|---|
| Матричное вычислительное устройство | 1979 |
|
SU809173A1 |
| Матричное вычислительное устройство | 1983 |
|
SU1149245A1 |
| Матричное устройство для возведенияВ КВАдРАТ | 1979 |
|
SU842804A1 |
| Матричное вычислительное устройство | 1979 |
|
SU824195A1 |
| Матричное вычислительное устройство | 1983 |
|
SU1124284A1 |
| Устройство для извлечения квадратного корня | 1976 |
|
SU661550A1 |
| Вычислительное устройство | 1981 |
|
SU1032454A1 |
| Многофункциональное вычислительное устройство | 1985 |
|
SU1293727A1 |
| Матричное вычислительное устройство | 1982 |
|
SU1024910A1 |
| Матричное устройство для деления | 1985 |
|
SU1247863A1 |
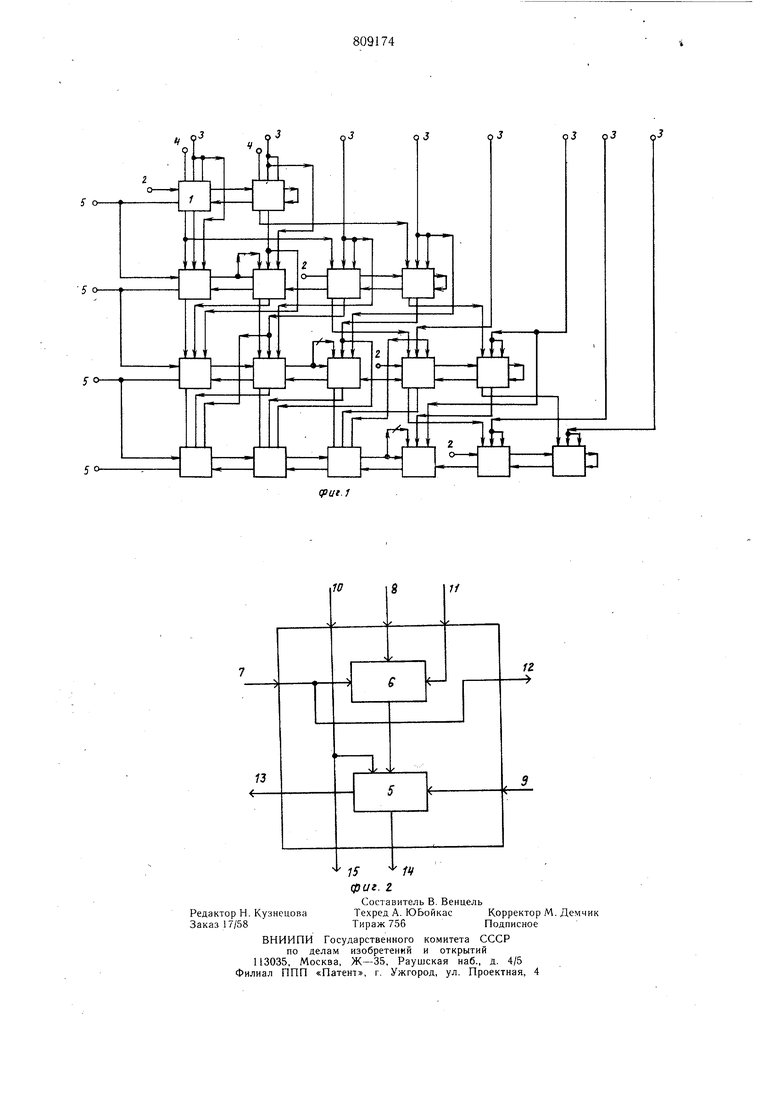

Изобретение относится к вычислительной технике и может быть использовано в быстродействующих процессорах и специализированных вычислительных устройствах. Известно матричное вычислительное устройство для извлечения квадратного корня 1. Данное матричное вычислительное устройство требует для своей реализации больших аппаратурных затрат и имеет неидентичные связи, что затрудняет его реализацию на больших интегральных схемах. Наиболее близким по технической суш,ности к предлагаемому устройству является матричное вычислительное устройство (МВУ) для извлечения квадратного . Каждая вычислительная ячейка включает сумматор по модулю два и сумматор и имеет четыре входа и четыре выхода 2. Недостатком устройства являются большие аппаратурные затраты при его реализации. Цель изобретения - сокращение аппаратурных затрат при реализации матричного вычислительного устройства. Поставленная цель достигается тем, что матричное вычислительное устройство, содержащее матрицу вычислительных ячеек, причем каждая вычислительная ячейка содержит сумматор, при этом первый вход вычислительной ячейки i-ой строки j-ro столбца соединен с первым выходом вычислительной ячейки i-ой строки (j-1)-го столбца, первый вход предпоследней вычислительной ячейки каждой строки соединен с первым входом устройства, первый вход вычислительной ячейки i-ой строки первого столбца соединен со вторым выходом вычислительной ячейки (i-1)-ой строки первого столбца, второй вход вычислительной ячейки i-ой строки j-ro столбца соединен с третьим выходом вычислительной ячейки (i-1) строки (j + l)-ro столбца, вторые Входы вычислительных ячеек второй строки первого и второго столбцов соединены с третьимя выходами вычислительных ячеек первой строки первого и второго столбцов соответственно, вторые входы двух последних вычислительных ячеек каждой строки соединены со вторыми входами устройства, третий вход вычислительной ячейки i-ой строки i-ro столбца соединен со вторым выходом вычислительной ячейки i-ой строки (j + l)-ro столбца, третий вход последней вычислительной ячейки каждой строки соединен с первым выходом последней вычислительной ячейки, четвертый выход вычислительной ячейки i-ой строки j-ro столбца соединен с четвертым входом вычислительной ячейки ()-ой строки j-ro столбца, четвертые выходы последних двух вычислительных ячеек i-ой строки соединены с четвертыми входами последних двух вычислительных ячеек (i+l)-oй строки соответственно, четвертые входы вычислительных ячеек первой строки соединены с третьими входами устройства, каждая вычислительная ячейка дополнительно содержит элемент И, причем в каждой вычислительной ячейке первый вход элемента И соединен с первым входом и с первым выходом вычислительной ячейки, второй вход элемента И соединен со вторым входом вычислительной ячейки, первый вход сумматора соединен с третьим входом вычислительной ячейки, четвертый вход вычислительной ячейки соединен со вторым входом сумматора, первый выход которого соединен со вторым, а второй выход - с третьим выходами вычислительной ячейки соответственно, четвертый выход вычислительной ячейки соединен со вторым входом сумматора, третий вход которого соединен с выходом элемента И, третий вход которого соединен с пятым входом вычислительной ячейки, причем пятый вход вычислительной ячейки i-ой строки j-ro столбца соединен со вторым входом вычислительной ячейки (i-l)-o.й строки (j + l)-ro столбца, пятые входы вычислительных ячеек второй строки первого и второго столбцов соединены со вторыми выходами вычислительных ячеек первой строки первого и второго столбцов соответственно, пятые входы последних двух вычислительных ячеек каждой строки соединены со вторыми входами устройства. На фиг. 1 изображена структурная схема матричного вычислительного устройства; на фиг. 2 - структурная схема вычислительной ячейки. Матричное вычислительное устройство содержит вычислительные ячейки 1, первые, вторые и третьи входы 2-4 устройства, выходы 5 устройства. Вычислительная ячейка (ВЯ) содержит сумматор 5, элемент И б, входы 7-11, выходы 12-15. Рассмотрим алгоритм извлечения квадратного корня, который используется в предлагаемом МВУ. В отличии от известного предлагаемое МВУ работает по восстанавливающему алгоритму извлечения квадратного корня. Пусть подкоренное выражение X представлено в данной системе счисления в прямом коде и нормализовано, т. е. 1. Пусть требуется найти квадратный корень из числа X, где X 0,010011001100... 1-ый шаг: предположим, что первая цифра результата равна единице. Провери.м это предположение. Это осуществляется вычитанием из первых двух цифр подкоренного выражения числа «01. Вычитание осуществляется сложением в дополнительном коде. Поэтому перенос в знаковый разряд означает положительность остатка. Отсутствие переноса означает отрицательность остатка. 01. В данном случае есть перенос в знаковый разряд, что означает положитель001 ность остатка. Следовательно, первая цифра результата равна «1. 2-ой щаг: в зависимости от знака остатка из первого щага берется либо уменьшаемое, либо остаток. Если остаток положительный, то бере.м сам остаток, иначе берется уменьшаемое. К этому числу добавляются еще цифры из подкоренного выражения. Это и есть уменьшаемое второго шага. Предположим, что вторая цифра результата равна единице. Проверка этого предположения осуществляется вычитанием из уменьшаемого числа ОС101, где С1 - первая цифра результата. QQQQ Переноса нет. Остаток отрицаiQii тельный. Следовательно, втоQ-rrrr- рая цифра результата равна нулю. 3-й шаг; отбрасываем первую цифру остатка и повторяем действия второго шага. Из вычитаемого вычитаем число ОС1С201, где С2 вторая цифра результата. 00011 Переноса нет. Остаток отрица. тельный. Третья цифра резуль011010 тата равна «О и так далее. МВУ работает следующим образом. Разряды подкоренного выражения поступают на матрицу. Первые два разряда поступают на вторые и пятые входы ВЯ первой строки, следующие два разряда поступают на вторые и пятые входы последних двух ВЯ второй строки, третья пара разрядов поступает на вторые и пятые входы последних двух ВЯ третьей строки и т. д. Действия в первой строке соответствуют действиям на первом шаге, а действия во второй строке соответствуют действиям на втором шаге и так далее. В зависимости от результата из (i-1)-ой строки, который поступает на первые выходы элементов И ВЯ i-ой строки, в качестве уменьшаемого i-ой строки выбирается остаток (i-1)-ой строки, поступающий на вторые входы элементов И ВЯг-ой строки или уменьшаемое (i-1)-ой строки, поступающее на третьи входы элементов ИВЯ i-ой строки. При единогласном значении первого входа элемента И он пропускает значение второго входа, а при нулевом значении первого входа - значение третьего входа. Вычитаемое подается на четвертые входы ВЯ в дополнительном коде. Определим аппаратурные затраты, необходимые при построении предлагаемого МВУ Предлагаемое МВУ и известное устройство т-ребуют для своей реализации одинаковое количество ВЯ, а именно 1/2(иЧ5п -2). Для конкретности оценим затраты оборудования, используя серию элементов 133. Реализация сумматора по модулю два в известном устройстве и элемента И в предлагаемом МВУ требует по три логических элемента из этой серии. Реализация сумматора, имеющего только прямые выходы и переноса, требует 10 логических элементов из этой- серии и требует прямые и инверсные шины всех входов. Входы сумматора в известном устройстве являются переносами с соседней ячейки справа, выход сумматора по модулю два и выход суммы одной ячейки верхнего ряда. Поэтому для сумматора по модулю два и выходов суммы и переноса двойных сумматоров требуется по инвертору , в то время как для предлагаемого МВУ требуется инвертировать только выход элемента И и выход переноса двойного сумматора, так как выход сумматора не поступает ни на какой сумматор. Эффективность изобретения заключается в выигрыше по оборудованию составляющего 1/2 (п +5п-2) инверторов, где 2п - разрядность подкоренного выражения, что составляет приблизительно 6% от общего числа оборудования. Формула изобретения Матричное вычислительное устройство, содержащее матрицу вычислительных ячеек, причем каждая вычислительная ячейка содержит сумматор, при этом первый вход вычислительной ячейки i-ой строки J-ro столбца матрицы соединен с первым выходом вычислительной ячейки 1-ой строки (J-1)-го столбца, первый вход пред-последней вычислительной ячейки каждой строки соединен с первым входом устройства, первый вход вычислительной ячейки i-ой строки первого столбца соединен со вторым выходом вычислительной ячейки (i-1)-ой строки первого столбца,второй вход вычислительной ячейки i-ой строки j-ro столбца соединен с третьим выходом вычислительной ячейки (i-1) -ой строки (j Ч-1) -го столбца, вторые входы вычислительных ячеек второй строки первого и второго столбцов соединены с третьими выходами вычислительных ячеек первой строки первого и второго столбцов соответственно, вторые входы двух последних вычислительных ячеек каждой строки соединены со вторыми входами устройства, третий вход вычислительной ячейки i-ой строки j-ro столбца соединен со вторым выходом вычислительной ячейки i-ой строки (J + 1)-го столбца, третий вход последней вычислительной ячейки каждой строки соединен с первым выходом последней вычислительной ячейки, четвертый выход вычислительнрй ячейки i-ой строки j-ro столбца соединен с четвертым входом вычислительной ячейки ()-oй строки j-ro столбца, четвертые выходы последних двух вычислительных ячеек i-ой строки соединены с четвертыми входами последних двух вычислительных ячеек (itI)-oй строки соответственно, четвертые входы вычислительных ячеек первой строки соединены с третьими входами устройства, отличающееся тем, что, с целью сокращения аппаратурных затрат, каждая вычислительная ячейка дополнительно содержит элемент И, причем в каждой вычислительной ячейке первый вход элемента И соединен с первым входом и с первым выходом вычислительной ячейки, второй вход элемента И соединен со вторым входом вычислительной ячейки, первый вход сумматора соединен с третьим входом вычислительной ячейки, четвертый вход вычислительной ячейки соединен со вторым входом сумматора, первый выход которого соединен со вторым, а второй выход - с третьим выходами вычислительной ячейки соответственно, четвертый выход вычислительной ячейки соединен со вторым входом сумматора, третий вход которого соединен с выходом элемента И, третий вход которого соединен с пятым входом вычислительной ячейки, причем пятый вход вычислительной ячейки i-ой строки j-ro столбца соединен со вторым входом вычислительной ячейки (i-1)-ой строки (j + l)-ro столбца, пятые входы вычислительных ячеек второй строки первого и второго столбцов соединены со вторыми входами вычислительных ячеек первой строки первого и второго столбцов соответственно, пятые входы последних двух вычислительных ячеек каждой строки соединены со вторыми входами устройства. Источники информации, принятые во внимание при экспертизе 1.Devries R. С., Chao М. Н. Fully iterative array for extracting square roots. «Electronics letters, 1970, vol. 6, № 8. 2.Шауман A. M. Матричное извлечение корня. Сб. «Вычислительная техника, ЛГУ, вып. б, с. 105-111 (прототип).
Авторы
Даты
1981-02-28—Публикация
1979-05-31—Подача