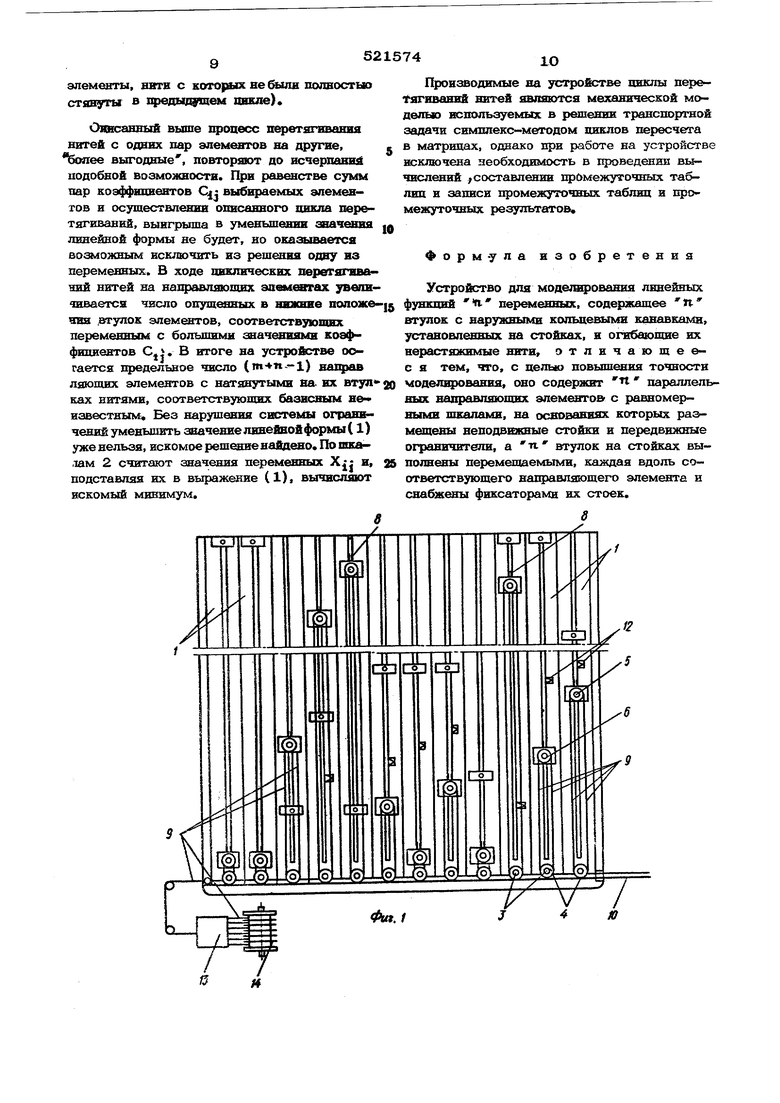
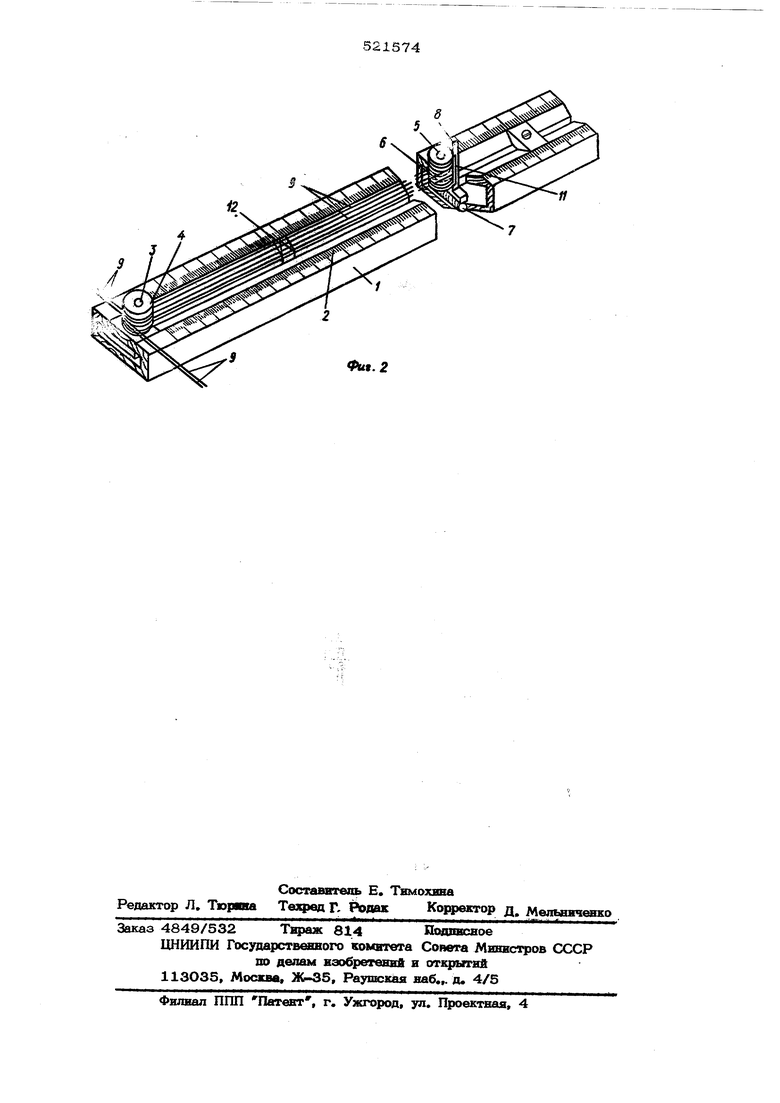
по b,.v,;i сяоей рабогой длине, В основани)Х Я;,и1р 1вляющих элсментов 1, на одном уровне укрсидеиы неподвижные стойки 3, иа ; (ждую 113 которых свободно, но без н:злн1ипег-о заоора, посажена втулка 4 с нару)Ю1ы ми кольцевыми канавками, расположенная против Щ) направляющего элемента. В каждой Но прорезей помещено по перемещаемой стойке 5, несущей свободно посаже ную втулку 6 с наружными кольпевыми клнавками м ручнор пружинный фиксатор 7 неремоиичемой стойки. Перемещение стоек 5 со втулками 6 ограничено передвижными ограничителями 8, Между втулками 4 и 6 разпесепы нити 9, уложенные в кольцевые канавки втулок. Фиксация шагов нитей в кан.11жа : втулок 4 осуществляется общим ыдиижнь1М плоским пругом Ю, а фиксация шагов литой в канавках втулок 6 - кромками с:педи (льны.х нланок 11, укрепленных .iia корпусах фиксаторов 7. На кромках прорезо направляющих элементов 1 помещены пружинные П(;ред1: и.жвые. индикаторы 12„ Нити IJ служат каждая для имитации онре- Д1-;1 ии й л пюйлой функции но числа фуик- .1ьных ограничений математической мпае.и ;мдачи и поступают на устройство Ч(из счотчик длин нитей 13 с катушки 14 которая может быт11 выполнена, нaпpи fep, из набора , фиксируемььх одно относиюльно другой и все имеете - относитель iiu корнуса катушки. Каждому из пероменных X j (j -1,2..., п. ) задачи соответствует свой направляющий элемент 1 со втулками 4 и 6. Огранич тели 8 установлены положении шкал 2, соответствующем с -щанлым пределам ния неременных X:. Каждое из с аданных ус/говиями функциональных ограничении; зддачн имитировано отдельной нитью, которая должна быть прак тически нерастяжимой. Общая длина участвутощих в имитации функционального .огранич ния участков нити соответствует сумме зна чений входящих в него неременных и изменяется в процессе рещения задачи. Каждая иа нитей подается с катущки 14 через счетчик 13 на втулку 4 соответствуюшей неподвижной стойки 3, огибает ее по четверти длины кольцевой канавки, посту пает на втулку 6 перемещаемой стойки 5, огибает ее по половине длины кольцевой ка лавки и возвращается на ту же втулку 4, огибает с противоположной стороны четверт длины кольцевой ее канавки и идет далее на следующую пару втулок 4 и 6 другого элемента 1, соответствующего другому пе- peMOHHosfy, входящему в это же функцгюнал HOG 01 IMUIимение .аднчи. Таким образом, обведены нитью все нары втулок 4 и 6, относя пиеся к одному и тому же функциональному ог{)аничению. Па последней из нтулок 4 1ить, после огибания последней из втулок 6, фиксируется. В случае, каждому из значений переменных X : соответствуют два участка нити О между втулками 4 и 6 одного и того же направлйющеги элемента 1, Общая вытравленная с катущкн 14 длина нити больше участвующей в имитации переменных ее длины на постоянную величину, равную сумме участков огибания нитью втулок 4 и 6 и участков перехода нити между втулками 4 разных направлшощих элементов, Эта, определяемая заранее величш1а, вычтена из показаний счетчика 13. На других кольцевых канавках втзлок 4 и 6 аналогично имитированы другие функциональные, огра ничения математической модели задачи линейного программирования. Фу 1кциональные оградичения, представляю- fi шие собой равелстиа вида .Е .., ...+ У(-Ь:, -,2,...п, где Ь-- постоянная величина, X О, имитированы в устройстве, как описано выше, нитями, длины которых равны tij (плюс - сумма постоянных по длине ее участков, не участвующих в имитации; также и везде в последующем изложении) в общем для всех функциональных ограничел ий задачи масштабе. Koiшы нитей фиксированы, а npii реигении задачи они должны находиться в натяжении за счет перемещения втулок 6 на определенных направляющих элементах. Функциональные ограничения, представляющие собой неравенства типа меньше или равно П ,+ .. + X,s Ъ также имитированы нитями, длины которых равны Ь{, их концы также фиксированы, но в процессе реще1П1я они могут оставать ся ненатянутыми. Функциональные ограничения, представляющие собой неравенства типа больше или равно Е XL XJ+XO ... Х„ Q; . J- Jл-сILL/ где fl.j - постоянная велич1ша, имитированы НИТЯМ, длины КОТОрЫХ ВЗЯТЫ раВНЫК И величинами С;, одним своим конном зафиксированы на какой-либо из втулок 4, а другим - поданы на катушку 14 и могут потравливаться с лее в процессе решения, ФункпиоНс.льные ограничения - двухсторо.нние неравенства типа Ь.С ,.. bj, где bj- , t)j - постояшше величины, имитированы на устройстве нитями длин bj , а в процессе операций могут потрагллми.-п ь- ся с катушки 14 нез,дфиксированнь ми KOillUlM (Д)у1-И0 концы их азфпкСПС IBciиы) до спо1 iu Tr:Ti5)qo;intx длш) t)j (или, 1(,)орит, сгглсиваться от bj до hi). гели на устр ойстве икнггировапа систеmма (. вида Д Х-- sV, L-1,2...,пг, i i,2,V..п, где V - подлежатая определению .еличш1а, то на него поданы и зафиксированы конном п д тей одинаковой длины, другие концы которых в процессе решенияпотравливаются (или выбираются) с катушки все одд овремелно на одинаковую длилу. Функциональные ограничения типа S X: {множество неремен- ieii 1 lel, 1 -.. мепиых X; разбито .на подкаюжества Ij и I,) имитируется }Ш устоойстве каждое двумя нитями, ОДИН конец каждой из которых зафиксировап,а два другие на катушку 14, В процессе операций пить, соответствующая обще1 части нераволстиа ( Ij ) мо жет потравливаться па устройство либо одновременно и на одинаковун; длину с другой нитью (1 ), либо отдельно от нее, котоfjaa в этом случае фиксиру(:тс:я. Функциональные ограничения - постоянны рвчзности переменных X.j,CX; i О, и - постоянная) .С X:-i:x- a имитируют„lei, 1 ieu 3 СИ на устройстве апалогично предыдущие, но с тем 1 отличием, что в промессе операций должна сохраняться постоянной разви-ца их длин а и потравливапи5( или стягивания нитей порознь исключены: нити 1 и 1 намотаны на катушку 14 бпфилярно Моделирований па устройстве условий задачи линейного программировапия заключается в реализации системы ее функциональных ограничений и получении допустимого плана решения задачи. Перед началом реализации системы огра ничений нити 9 на устройстве разнесены по втулкам 4 и 6 направляющих элементов 1, как описано выше, в соответствии с задаш1 ми функциональными ограничениями, но не натянуты. Ограничители 8 поставлены на шкапах 2 в положения, соответствующие за данным пределам изменения каждой из пере менных Х-. Если нижний предел изменения переменной - нуль (XJ О), необходимост в ограничителе 8 отсутствует. Втулки 6 перемещаемых стоек находятся в Нижних положениях 1при ) или на значениях шкал 2, отвечающих нижним пределам изменения переменных, отличным от нуля (Х O-j-). Реализация систем функциональных огра ничений на устройстве в зависимости от вида математической модели имеет свои особенности. Процесс поясняется на пример .;амкнутой транспортной задачи линейного программирования. Задача. Имеется тп пунктов производства однородного или взаимозаменяемого продукта и н пунктов его потребления. Заданы объем производства ,а: каждого из пунктов производства и размеры сщэоса bj nyjtKTa потребления (в тех же единицах). Извест; ы также расходы С j свргмпные с перевозкой едшпшы продукта из калодого пункта производства в пункт потребления, Xj.- количество единиц продукта,, поставляемое из какого-либо пункта прои;)водства ( 1 ) в какой-лнГя) пункт потребления ( J ), , Суммарные затраты нл Перевозку продукта из всех пунктов npon vводства во все пункты потребления должпы быть мш1има льным и L S Ё,С,.Х,- --«ии. i( 11 TpooYCiica сос:таБ1ггь план ii: ic;v4cjr)K, обеспоч11В ЮИ},н паиболо эколог г-;лм путем удовлетвпрсиие сг):осл и-нктов потреб. засГ-Т реали; ации , продукта, произведи и о го П.ССМ1 ггу и к.г Г1, i .м-чьмводства. При этеж условнл ri iiinv . vaOfwioTBOjjo. ПИЯ.спроса S.rS. а весь производствелный jipa,M,v: г, )|1ыи требуется развести EK,; a-, Система разнесенн:;гч на (-ч ч } направляющих элементах ус1рглК;ть. питой О j и П нитей Ъ такова, тг) Hirpo;.s втулки 4 и 6 каждого ,|;№я1д:;-; :1ЛСк-и:;лта всегда проходят, по KpiaHHCiii мере, pKi-: нити, принадлежащие: oru.a .- (:;,;ггоме фу1П циопалт ных ограничений (2), ;; другая системе ограничений (3), Из оощ.ой с-.овокушшсти постошп ых воличил ( i 1,2..,, in ) и bj ( j l,2,,..,tl ) ВГ.1-бирают наименьшую, соатветс-.твующую наиболее короткой с: напрпг.ляющих элементов с паимеиыши.ш.- Д-оя г ыбр;:и1 ного равенства значениям коэ44 Ц 1Кнтов Cii в линейной форме (1), производят натягивания jniTn поочероднь м- подъемом втулок 6 в верхние предсиы ые положопия, последовательпо переходя к больцщм з ачениям С|-, Когда наикратчайшая jurrb натянута, переходит к натяжению следующей в порядке возрастания воличш О,- и I) кити. Если в новом и прежнем фупкционал - ных ограничениях нет общего перомешюго, т. е. оба они относятся к одной иа cnCTeNi ( 2-) или (3), то натяж:ение этой нити осуиюствляют также. Если же в пгрвом и втором ограничениях имеется общая иеромелиая (нити имеют общий направляющий элемент то натяжение начинают с соответ-ствующей ей втулки 6, опуская при необходимости рдновремоино на ту же величину уже поднятые втулки 6, на которых натянута пер™ вая нить (или предыдущие нити), но имеющие наиболыиие значения коэффициентов C Ранее натянутая нить ( или, нити) при этом не ослабляется. До полного натяжения второй (или очэредной) нити последовательно переходят:к втулкам 6 с возрастающими коэффициентами С-, начиная с наименьши в данном равенстве, приводя их в верхние предельные положения, при необходимости опуская ранее уже поднятые втулки 6 с большими, чем у поднимаемых втулок, значениями Cj; , приводя их в нижние предель ные положения. Ранее натянутые нити при этом не ослабляются. Точно также поступают при натяжении всех последующих нитей, но при этом из числа опускаемых втулок 6 исключают те, обе нити на которых (принадлежащие разным системам) уже находятся в натяжении Положение втулок 6 на направляющих элементах, соответствующее натяжению всех ьитей и: и Ъ, моделирует на устройстве допустимый план решения задачи. Если по условиям задачи, вместо систе мы функциональных ограничений ( 3), на устройстве имитирована система равенств типа меньше или равно |/iJ« L, 1 1,2,... m ( модель открытой транспортной задачи линейного программирования), то производят выше описанное натяжение нитей подъемом втулок 6, начиная с нитей лишь системы ( Ъ; , а к нитям Qf обращаются тогда, когда они начинают препятствовать полному натяжению нитей Ь-, При этом осуше вляют описанные выше парные встречные перемещения втулок 6 на направляющих элементах, добиваясь натяжения всех нитей t)j ,, Особенности реализации на устройстве с тем ограничений вида С. X . 5 Е X. i lei lelj 3,1 ключается, в следующем. Поскольку нити I и 1 поступают на устройство слоiженлыми вместе, они получают одинаковые приращения длины. Подъемы втулок 6 в ве ние предельные положения начинают с направляющих элементов 1, относящихся к мн жеству I j (в порядке нарастания коэффициентов Cji), Если при натянутой нити , при последующем; подъеме втулок 6, длины нити оказываетотносящихся к I фиксируют, а нит ся недостаточно, нить потравливают до ее натяжения втулка Если на устройстве реализуется система равенства вида X Е Х- а iei, ieij, где а - постоянная величшш, то автономные потравливгшия или выбирания каждой из двух нитей недопустимы, . Получение искомого решения; задачи в виде набора значений переменных-оптимизация допустимого плана - заключается в установлении на устройстве их значений обеспечивающих в сумме максимум или минимум целевой функции при сохраиении функциональных ограничений и ограничений переменных.. Процесс решения поясняется на примере изложенной выше замкнутой транспортной задачи линейного программирования. На устройстве реализованы системы oi раничений (2) и (3) нити натян ты, требуется определить минимум линейной формы (1)m п L-E KC..X-.MMH. i-1 i-i и M Из числа направляющих элементов с подпятык и втулками выбирают два таких, чтобы у них не имелось общей нити и сумма соответствующих им коэффициентов Cj- линейной формы была при этом наибольшей. Пусть это будут, .например, направляющие элементы Х, иХ ,а нити с этих элементов могут быть натянуты на направляющих элементах Xj и X.j , втулки которых не находятся в верхних предельных положе- лнях, а сумма соответствующих им коэффициентов Cj- меньше суммы первых двух, т, е. ,,.4 i, После выбора таких направляюи1их элементов, втулку направляющего элемента Хдд опускают. При этом натяиутые на них нити и 6 I ослабляются,Затем опускают втулку направляющего элемента Х 2-создавая слабину нат5шутых на нем ниа втулку элемента X тей а., и -С j одловремершо поднимают,; выбирая слабину нитей а (с элемёнта( ) и (с элемента Х ). В предельных положениях фиксируют втулки Х. 2. и X J , (если они их достигли). Оставшиеся ослабленными нити а и Ъд натягивают подъемом втулки элемента Х д которую фиксируют. Поскольк нити а,, , 4 ослаблялись и натягивались на одинаковые длины, соответствующие функциональные ограничения остались удовлетворяющими условиям задачи, а значениелинейной формы (1) уменьшялсюь. / Далее аналогично выбирают следующую пару поднятых втулок и пару втулок им со отвстств5-ощую (включая и те направляющие элементы, ввти с котораых вебылл полностью стянуты в щ еаыщт&л ), Отагсаввый выше пропесс перетягнвання нитей с одвих пар элемевтов на другие, пбояее выгодные , повторяют до исчерпаввй подобной возможности. При равенстве сумм пар коаффшшентов Cjj выбираемых элементов и осуществлении описанного цикла перетягиваний, выигрыша в уменьшении гвачення линейной формы не будет, но оказывается возможным исключить из решения одву из переменных. В ходе циклических церегягнваний нитей на наюравляющих эавмввтах уьепя-швается число опущенных в шишве цодоже НИН .втулок элементов, соответствующих переменным с большими значениями коаффиоиентов Cjj. В итоге на устройстве оо J гается щюдельное число () яяпряц лающих элементов с натянутыми на- их втуп ках нитями, соответствующих базисным ие известным. Без нарушения системы orfuaasf ченийуменыиить значение линейной формы (1) уже нельзя, искомое решение найдено По шка- ,там 2 считают значения переменных и, подставляя их в выражение (1), вычисляют искомый минимум. Производимые на устройстве циклы пере- Гягиваний нитей являются механической моделью используемых в решении транспортной задачи симплекс-методом цивиюв пересчета в матрндах, однако при работе на устройстве исключена необходимость в проведении вычислений ; составлении тфомежуточных таблиц и записи промежуточных таблиц и промежуточных результатов, Форм-ула изобретениа Устройство для модещрования линейных функций а- переменных, содержащее П втулок с наружными кольцевыми канавками, установленШ)1х на стойках, и огабаюпше их иерастяжимые нити, отличающеес я тем, что, с целью повышения точности моделирования, оно содержит П параллельных направляющих элементов с равномерными шкалами, на основаниях которых размещены неподвижные стойки и передвижные ограничители, а п. втулок на стойках выполнены перемещаемыми, каждая вдоль соответствующего направляющего элемента и снабжены фиксаторами их стоек.
ut. 2



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для решения систем линейных уравнений и неравенств | 1979 |
|
SU1003100A1 |
| Устройство для моделирования систем линейных уравнений и неравенств | 1976 |
|
SU613331A1 |
| Устройство для решения систем уравнений и неравенств | 1977 |
|
SU752385A1 |
| ПАТЕНТНО- -j^^ ТУХ.МЯ'!Р.Си'АЯ ^^ БИБЛИОТЕКАiО. Я. Серов | 1966 |
|
SU181304A1 |
| ПРИБОР ДЛЯ ПРОЕКТИРОВАНИЯ ПОДЪЕЗДНЫХ ПУТЕЙ К МАГИСТРАЛЬНЫМ ДОРОГАМ | 1970 |
|
SU267934A1 |
| ПРИБОР ДЛЯ ВЫЧЕРЧИВАНИЯ МНОГОФОКУСНЫХ КРИВЫХ С ФОКАЛЬНЫМ СВОЙСТВОМ ПОСТОЯНСТВА СУММЫ РАССТОЯНИЙ | 1966 |
|
SU214823A1 |
| Регулируемое лекало | 1973 |
|
SU500081A1 |
| ГИБКИЙ ЭКРАН С ПРИВОДОМ И ЭЛЕКТРИЧЕСКОЙ СИСТЕМОЙ УПРАВЛЕНИЯ ЗАЩИТНЫМИ ЭКРАНАМИ | 2022 |
|
RU2779606C1 |
| Крутильные весы | 1977 |
|
SU693323A1 |
| Направляющий механизм верхней нитки швейной машины | 1986 |
|
SU1613000A3 |



Авторы
Даты
1976-07-15—Публикация
1974-03-01—Подача