При проектировании различного рода зубчатых зацеплений весьма существенное значение имеет правильный расчет или построение кривых, определяющих корневую часть зубьев. К сожалению, как то, так и другое связано с исключительно больщой и кропотливой работой. В виду изложенного, единственно правильным методом решения задачи следует признать получение подобных кривых механически, путем создания соответственного чертежного прибора, автоматически (при надлежащей настройке) вычерчивающего подобную кривую. Практически это приводит к построению предельных удлиненных эвольвент, удлиненных эпициклоид и эквидистантных к ним кривых. Так как последние всегда могут быть получены по первым, например, путем воспроизведения огибающих к окружностям с центрами, лежащими на основной кривой, то дело сводится лищь к получению указанных удлиненных рулетт.
Технически задача может быть разрешена двояко: либо созданием прибора максимальной точности, строящего кривую в натуральную величину профиля (тип „разметочного прибора), либо созданием чисто чертежного прибора, производящего построение в сильно увеличенном масштабе, что допускает применение некоторых специальных узлов, например, „планиметрических роликов и т. п., недопустимых в разметочных приборах.
Приборы первого типа могут быть легко осуществлены в отношении удлиненной эвольвенты на базе обычного эвольвентометра. Однако, в отношении получения удлиненных эпициклоид дело обстоит здесь значительно сложнее. Наоборот, прибор чертежного типа осуществляется легко как для удлиненной эвольвенты, так и для удлиненной циклоиды.
Предлагаемый прибор предназначен для вычерчивания циклоидальных кривых и выполнен в виде поворотной вокруг некоторого центра щтанги, шарнирно соединенной со стержнем, несущим пишущий орган и в свою очередь шарнирно связанным со стержнем, проходящим через подвижной по штанге шарнир и снабженным роликом.
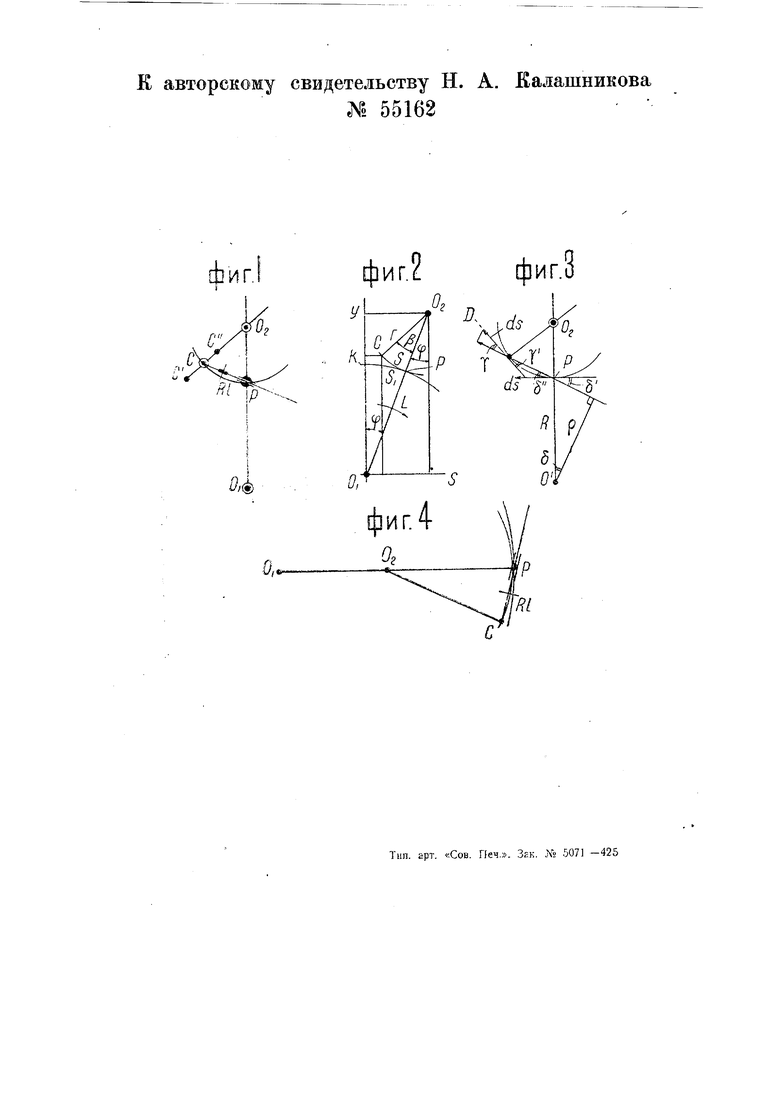
На чертеже фиг. 1 изображает схематический вид предлагаемого прибора для вычерчивания циклоидальных кривых, фиг. 2 и 3 - схемы, поясняющие его действие, фиг. 4 - видоизменение предлагаемого прибора.
Предлагаемый прибор для вычерчивания циклоидальных кривых выполнен в виде четырехзвенного механизма и состоит из основной штанги QI О,, устанавливаемой в точке Oj, как в неподвижном центре, из соединенного шарнирно с подвижным центром Оз вспомогательного стержня и из стержня СР, свободно скользящего в направляющей, вращающейся вокруг точки Р пересечения штанги Oi О, и стержня СР. Стержень СР снабжен катящимся по бумаге заостренным роликом ,, препятствующим перемещениям бумаги в направлении стержня СР, но свободно допускающим перпендикулярные к нему перемещения и повороты. При повороте штанги О, О вокруг точки Од карандаш, установленный в точке С, С или С, будет чертить на бумаге нормальную, удлиненную или укороченную эпициклоиду соответственно в том случае, если О,,Р, что достигается настройкой (Oi, С и Р путем зажима устанавливаются на произвольном от О, расстоянии).
Чтобы доказать сказанное, достаточно, конечно, установить эпицикличность движения точки С, так как С и С жестко х:вязаны с , но и то же время лежат на иных радиусах, т. е. на иных расстояниях от О,.
Рассмотрим предварительно возможные движения точки С при отсутствии связи стержнем СР, как показано на схеме (фиг. 2). Если бы стержень был радиусом окружности (центр OJ, перекатываемой без скольжения по другой (центр О,) штангой OiOz, то наличие эпициклоиды, как следа точки С, было бы несомненно по определению этой кривой. Следовательно, для точки С эпициклоида ябляется одной из возможных траекторий и для получения
именно этой кривой достаточно наложить такие вспомогательные связи, которые исключали бы возможность иных движений. Формально это выражается следующим образом. При отсутствии каких-либо заданных соотношений между поворотами штанги ОдОг и стерлсня О%С уравнение точки С в декартовых координатах по схеме (фиг. 2) будет:
X-Lsln - rsin (Р + ) Y Lcosf - г cos ( 4 )
где L поворота L от исходного положения К; Р - угол между Лиг.
Если обозначить L через R-}-r (где R OiK), то предыдущие уравнения примут вид:
X (R-i-r) sincp -rsin(p + cp) Y- () cost -/ cos (P + f)
С другой стороны, если бы окружность радиуса г по предыдущему перекатывалась по окружности радиуса R, т. е. дуги КР и СР были бы всегда равны, то добавочным условием к предыдущим уравнениям явилось бы лишь К.Р СР 1 R(f или
.
откуда самые уравнения приобрели бы вид:
X() sin-f-rsin-t : p
r() cost -г
что, как известно, и является уравнениями эпициклоиды.
Таким образом доказано, что подлежащая наложению на схему (фиг. 2) связь должна лишь обеспечить
гр или 5i 5 или A5i Д5 где
S /
Для доказательства, что вводимая схемой (фиг. 2) связь СР этому условию удовлетворяет, рассмотрим для простоты эту схему (фиг. 3) относительно штанги OiOa как неподвижной, предполагая, что перемещающийся ролик может увлекать за собой бумагу лишь в направлении слагаемой PC. Обозначим бесконечно малое дуговое перемещение точки С вектором ds, направленным по касательной СД. Проекция этого вектора на СР равна dscosf. Именно это перемещение передается по условию бумаге. Следовательно, ее угловое перемещение определится, как
, ds cos Y aq ,
где p - переменное расстояние линии СР от центра Oi.
Дуговое перемещение на радиусе будет:
rf5, il-/
Для тождества необходимо, следовательно, чтобы -H- cosr,
/
но так как,-4- cos о, то условие перекатывания приводится к необходимости Y 3, но S 8, как углы между перпена,икулярами, 8 5 и т т как накрест лежащие, и, наконец, о f, как углы между касательными и соответственной хордой круга.
Следовательно, S Y и , откуда и интегралы дуг могут отличаться лищь на начальную постоянную, что и требовалось доказать.
Ясно, что перемена О; и Р местами (фиг. 4) приведет аналогично к гипоциклическому, а поступательное перемещение OiOj к ортоциклическому приборам. Однако эти разновидности не представляют такого интереса, как эпициклический прибор, необходимость в котором достаточно понятна из условий профилирования фасонного инструмента, где подобный прибор может оказаться особенно полезным.
Предмет т зобретения.
1.Прибор для зычерчявания циклоидальных кривых (эпициклоиды, гипоциклоиды, ортоциклоиды), отличающийся тем, что он выполнен в виде поворотной вокруг центра О, щтанги OjO;, щарнирно соединенной со стержнем О2С, несущим пишущий орган и шарнирно связанным со стержнем СР, проходящим через подвижный по штанге шарнир Р и снабженным роликом RL.
2.Форма выполнения прибора по п. 1, отличающаяся тем, что для возможности вычерчивания ортоциклоид штанга выполнена продольно перемещающейся. к авторскому свидетельству Н. № 55162 А. Калашникова


| название | год | авторы | номер документа |
|---|---|---|---|
| Прибор для вычерчивания математических кривых | 1986 |
|
SU1449359A1 |
| Способ изготовления зубцов циклоидальных зацеплений сателлитов планетарных передач редукторов | 1946 |
|
SU68422A1 |
| ЦИКЛОИДАЛЬНО-ЭВОЛЬВЕНТНОЕ ЗУБЧАТОЕ ЗАЦЕПЛЕНИЕ | 1993 |
|
RU2113643C1 |
| ПРИБОР ДЛЯ ВЫЧЕРЧИВАНИЯ ПРОЕКЦИИ ПОВЕРХНОСТИ СПИРАЛИ | 1937 |
|
SU56100A1 |
| Внецентроидное гипоциклоидальное зацепление с внутренними профилями | 1950 |
|
SU93032A1 |
| Устройство для вычерчивания лекальных кривых | 1990 |
|
SU1805067A1 |
| РОТОРНЫЙ ПРЯМОЗУБЫЙ КОМПРЕССОР | 2000 |
|
RU2180053C2 |
| РОТОРНО-ВРАЩАТЕЛЬНАЯ МАШИНА | 1996 |
|
RU2113622C1 |
| Циркуль | 1990 |
|
SU1754482A1 |
| Прибор для черчения и огибания кривых | 1990 |
|
SU1818256A1 |

фиг.2фиг.З
О,
Авторы
Даты
1939-01-01—Публикация
1936-02-01—Подача