При конструировании планетарных редукторов, обладающих высоким коэффициенюм полезного действия при значительных передаточных отношениях, существенное значение имеет продолжительность зацепления, определяющая величину контактных напряжений на поверхностях элементов внутреннего зацепления.
Предлагаемое внецентроидное гипоциклоидальное зацепление по сравнению с известными зацеплениями - эвольвентным, внецентроидным циклоидальным, внецентроидным цевочным эпициклоидальным и внецентроидным цевочным гипоциклоидальным - позволяет увеличить продолжительность зацепления и уменьщить контактные напряжения на поверхностях элементов внутреннего зацепления. Это достигается тем, что в качестве исходной кривой зубьев внешнего колеса принята растянутая гипоциклоида, а в качестве кривой зубьев внутреннего колеса принята сопряженная огибающая гипоциклоид при внешнем качении двух центроид.
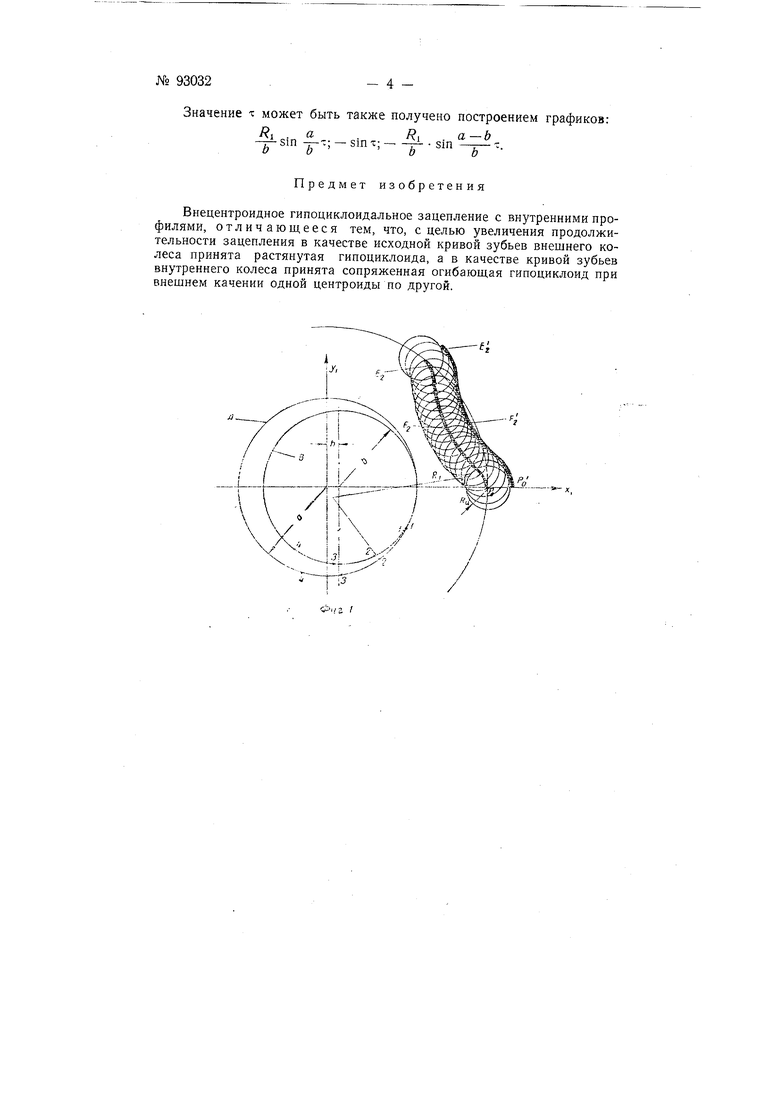
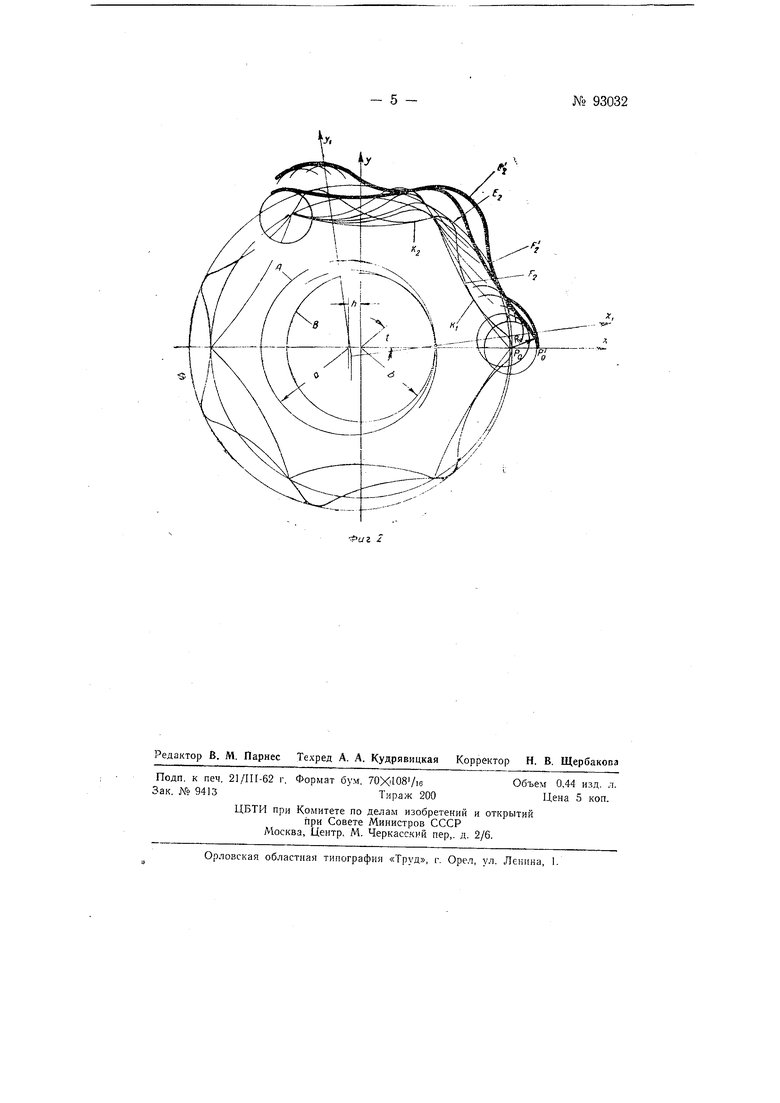
На фиг. I и 2 изображено графическое построение внецентроидного гипоциклоидального зацепления с внутренними профилями.
Это построение и его теоретическое обоснование заключаются в следующем.
Если в качестве исходной кривой профиля зубьев внещнего колеса примем растянутую гипоциклоиду , то для получения этой гипоциклоиды следует воспользоваться двумя окружностями: большой А и малой В (фиг. 1). При качении окружности R по окружности А точка РО, связанная с В, по лежащая вне ее. будет описывать кривую Р.гЕ,.
№ 93032- 2 При полном цикле обкатывания, меняя значение переменного параметра до 360/2. (где: 2j - число зубьев внутреннего колеса,д -
ЧИСЛО зубьев внешнего колеса), получим полную растянутую гипоциклоиду. Ее эквидистанта при образующей окружности ц служит профилем зубьев внешнего колеса.
Условием замкнутости кривой является равенство: b a b+h и
где: b- радиус центроиды внутреннего колеса, а - радиус центроиды внешнего колеса, h - эксцентриситет окружностей Л и В. Уравнение растянутой гипоциклоиды:
.1 /г cos + 1 -г- cos -.
У А si« + 1 -г- зшт:,
где: t - переменный параметр в градусах;
- радиус делительной окружности внутреннего колеса. Соответственно уравнение кривой эквидистантного профиля будет:
-,Х + . .
+ y
Для образования профиля зубьев внутреннего колеса примем способ построения сопряженной огибаюшей, когда даны две центроиды Л и j8 и кривая профиля зуба колеса Л.
Для получения сопряженного профиля внутреннего колеса В (фиг. 2) поворачивают внешнюю окружность Л в различные положения по отношению к внутренней окружности В и для каждого положения вычерчивают кривую . Огибаюш,ая этих кривых дает сопрял енный профиль зубьев внутреннего колеса В.
Для упрощения решения задачи по отысканию уравнений профиля зубьев внутреннего колеса предварительно найдем уравнение огибаюшей к растянутой гипоциклоиде Я F, Е,, после чего найдем уравнение кривой профиля внутреннего колеса.
Для определения уравнения огибающей рассмотрим две близкие кривые семейства. Уравнение растянутой гипоциклоиды в системе х, у (фиг. 2) примет вид:
X - - t - -1 (а b) cost - (- t)
CtCtf,
hh
у - - t+ yjcos - t - {a - b} sifit (i t).
где - переменный параметр, определяющий положение точки на кривой в системе ,Viyi; t -переменный параметр, определяющий положение самой кривой в системе х, у.
Уравнение, связывающее -: и г, как известно, имеет вид:
д-Ь (3(} df
dt t- dt Т ци из фо гд K Тогда уравнение огибающей примет вид: у р. г; dtp ( (т В развернутом виде уравнение огибающей будет: t i. / - , п (а - Ь , а-i л ; (а - 6) cos (т . tj + (- + - tj / г,л./ -,п ./а -&,а -&, у - (а - &) sin ( . /; j + sin (- - Н -f). а./ , b . К i b . a-b , -7- т - sin I t Hг; ) + -т- sin I - tГ- г; j O. b / b ab / Точка соприкосновения огибающей с исходной растянутой гипоклоидой находится при 0. Значение параметра -: точек соприкосновения может быть найдено уравнения связи, приведенного к виду R . а .R, а - 2a - b r- sin -г- -г -sin sin -7- : sin -pr-l ,- 1 b bbb2 b при этом число касаний, равное числу зубьев Zj, найдется из рмул: sin 21п е я - любое число О, 1, 2, 3....Zj. Значение т для второй точки пары сопряженных зубьев (точки , К.2....Кп} (фиг. 2) получим из уравнения: RI 2а-Ьt т ° г- -°т °Это уравнение приводится к известной формуле: Лcos rt т, - cos m. - N cos /г TJ - (9) cos т + 4-1-) sin tj cos- 1 - - cos ti - - sin i i + T /J L + COS -TI - . № 93032 х (,t), У - Т (пО, -(а- b) cost, -(а - b) slnt, i)°:
Значение t может быть также получено построением
Ri . а.
5Ш.;-5Шт;
предмет изобретения
Внецентроидное гипоциклоидальное зацепление с внутренними профилями, отличающееся тем, что, с целью увеличения продолжительности зацепления в качестве исходной кривой зубьев внешнего колеса принята растянутая гипоциклоида, а в качестве кривой зубьев внутреннего колеса принята сопряженная огибающая гипоциклоид при внешнем качении одной центроиды по другой.
а -Ь
b b


| название | год | авторы | номер документа |
|---|---|---|---|
| Способ изготовления зубцов циклоидальных зацеплений сателлитов планетарных передач редукторов | 1946 |
|
SU68422A1 |
| Способ нарезания зубьев эпи- и гипоциклоидальных зацеплений | 1952 |
|
SU96189A1 |
| Гипоциклоидальное зубчатое зацепление | 2018 |
|
RU2704657C2 |
| Гидромотор-барабан лебедки | 1986 |
|
SU1463711A2 |
| РОТОРНО-ВРАЩАТЕЛЬНАЯ МАШИНА | 1996 |
|
RU2113622C1 |
| ГЕРОТОРНЫЙ МЕХАНИЗМ | 2002 |
|
RU2250340C2 |
| Способ обработки сложных профилей | 1980 |
|
SU952446A1 |
| Зубчатая передача | 1986 |
|
SU1323796A1 |
| ГЕРОТОРНЫЙ МЕХАНИЗМ ВИНТОВОГО ЗАБОЙНОГО ДВИГАТЕЛЯ | 2007 |
|
RU2360129C2 |
| ЦИКЛОИДАЛЬНО-ЭВОЛЬВЕНТНОЕ ЗУБЧАТОЕ ЗАЦЕПЛЕНИЕ | 1993 |
|
RU2113643C1 |


тл
Авторы
Даты
1951-01-01—Публикация
1950-08-03—Подача