.Предметом изобрет;ения является сопло, ограниченное двумя соосными однополостными гиперболоидами, соединенными между собой направляющими лонатками, образующими систему вращения.
Известные сопла подобной конструкции предназначаются для реализации потока, в котором частицы газа движутся по прямым линиям Сно образующим семейства соосных однополостных гиперболоидов, представляющих поверхности тока).
Особенность сопел такого рода состоит в том, что при поддержании на входе в сопло потока в равномерном состоянии, независимо от значения параметров этого состояния, поток на выходе из сопла будет оставаться всегда равномерным.
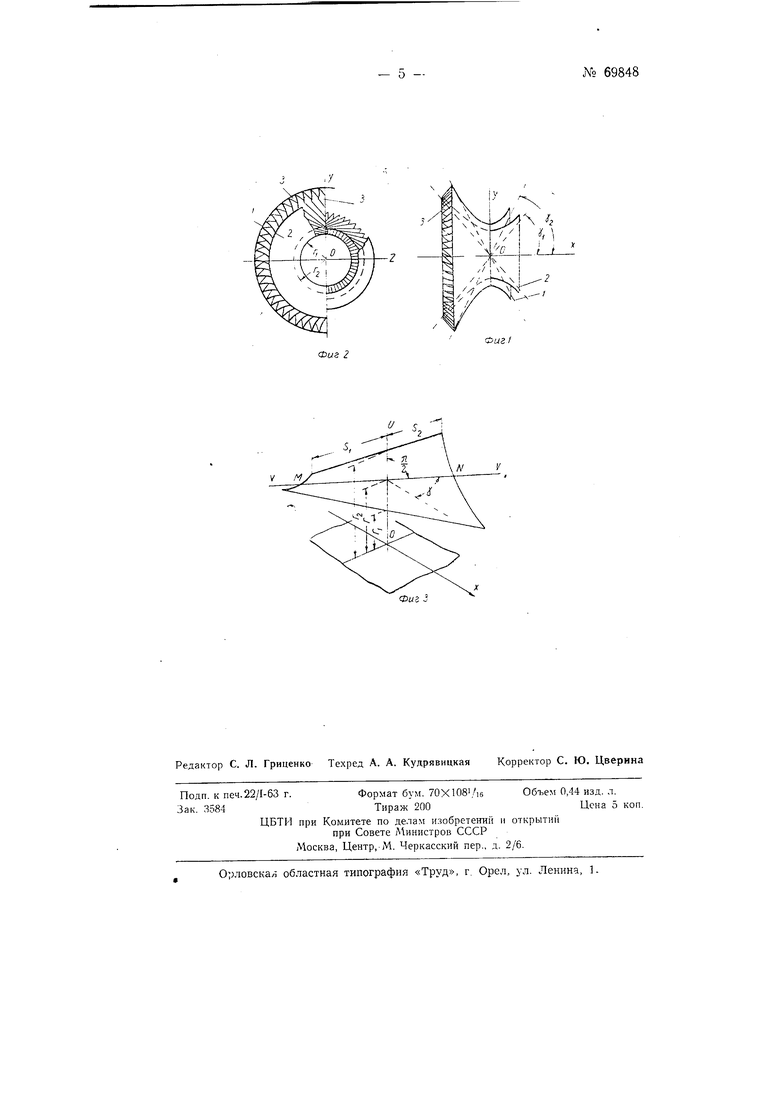
В предлагаемом сопле граничные гиперболоиды 1 п 2 (фиг. 1), оставаясь соосными (за ось гиперболоидов принимаем ось л-), имеют различные асимптотические конусы, причем задается строгая зависимость между углом у образующей асимптотического конуса гиперболоида с осью X и радиусом г горлового круга гиперболоида:
tgT Ксе --1 ,(1)
где С и К - произвольные постоянные, причем С - 1, .е- основание натуральных логарифмов.
Формула (1) служит для построения не только гиперболоидов, но и направляющих лопаток. Горловые круги граничных гиперболоидов предполагаются лежащими в одной плоскости ортогональной оси системы. Возьмем в этой плоскости прямую U (фиг. 3), проходящую через общий центр горловых кругов. Если вдоль этой прямой U перемещать прямую V так, чтобы она, оставаясь ортогональной прямой (J , была наклонена к оси под углом Y связанным с расстоянием г между осью -v и прямой V с помощью формулы (1), то геометрическое место прямых определяет прямой коноид со стрикционной прямой (J . Если на пря№ 69848
мой Квзять по обе стороны от прямой U точки М и Л, удаленные от и па расстояния 5 и S.,, то прп движенпи прямой V точкп М н Л опишут на эквпдпстанты S п 59.
В предлагаемом сопле за направляюш,ую лопатку 3 (фпг. I и 2) принят кусок коноида S , ограниченный эквидистантамп 5) S и прямолинейными образующими, удаленными от оси х на расстояния г и г., (фиг. 3).
Если S и г принять за параметры поверхности, то декартовы коордннаты X, у, Z выражаются через 5 и г следующим образом:
что после исключения s и / дает:
Z- -: к- .- (3)
Для определения давления р, плотности о и модуля скорости w служат уравнения:
(4)
- С, - О 1 :. :-С, - о«- ;(5)
2п - 2/г- 1
рг. - ;,(6)
А г К.9 + 1,(7)
где 5 - расстояние по прямолинейной образующей соответствующего коноида от плоскости горловых кругов.
Из уравнений (4), (5), (6), (7) следует, что эквидистантные поверхности, получающиеся вращение.м эквидистантных линий s - const около оси X, являются поверхностями равномерного состояния потока.
Если в плоскости горловых кругов поток достигает критического состояния, то при переходе через эту плоскость поток перерождается из дозвукового в сверхзвуковой и наоборот. Таким образом, предлагаемое сопло может выполнять функцию сопла Лаваля.
Обоснование уравнений, определяющих геометрию предлагаемого сопла и состояние потока в нем, получается из рассмотрения нижеследующей модели идеального потока с непрерывно распределенными бесконечно тонкими лопатками (связями), образующими систему вращения.
Пусть вектор
R R (s,r,9)(8)
определяет три непрерывных семейства поверхностей .s const; r- const; ср-const, удовлетворяющих следующим условиям.
Семейство f const есть семейство гладких непересекающихся поверхностей, образующих систему вращения. Примем за ось системы ось х. Семейство г const есть семейство гладких непересекающихся соосных поверхностей вращения с осью вращения х.
Если - некоторая гладкая поверхность вращения, соосная с семейством / const, но не принадлежащая ему, .тс за семейство s const принимаем семейство эквидистантных поверхностей в предположении, что измерение расстояний производится от поверхности s : О по дугам
конгруэнции кривых г - const, г:; COnst.
Пусть в пространстве s, г, у совершается установившийся поток идеального газа через поверхность s : 0.
Считая, что семейство поверхностей з - const является семейством связей потока (т. е. является семейством непрерывно распределенных бесконечно тонких лопаток), будем искать это семейство в предположении, что поток совершается по конгруэншш прямолинейных образующих семейства г const при условии равномерного состояния потока на поверхности s О (или на какой-либо другой поверхности s Si).
Поток и связи определяются из уравнений:
-- grad (;;) -;--A arad (.),(9)
. fjь
d где положено те , i - коэффициент реакции связи
cs - const, a - смешанное произведение, ,
значение Д гфи s :: 0.
В случае потока по конгруэнции прямых система (9) приводится к системе:
.- -1-Со- р-: - -С„- 0„-; (10)
2п-12«--1
dR dR 0,(9А, ds дг 1 dsдг А/ dR dR где А , а . - скалярное АО ds , дг I торов
В рассматриваемом случае семейство r- const является семейством соосных однополостных гиперболоидов.
Пусть поверхность s - О является поверхностью горловых кругов этого семейства и путь уравнением меридиана поверхности s О будет X - а(г.
Если г , у являются криволинейными полярными координатами плоскости (у, г, причем линией ts const является проекция на плоскость - (у, г следа связи « С на поверхности 5 0, которая Б- обычных полярных координатах Q, г представляется уравнением (r, то уравнения конгруэнции прямолинейных образующих семейства г . const запишутся в виде: л- а (г)
у Lr; rcos f + 9о ( ) -г , ср -г (г ;
г г - г sin -f + -f о (г) -f - cos f+tf о (г) ,(11)
я 69848
Р С, ;
fjffi)A . ,
I dR dR dR .
ds or d I dRdR dsdr
&Ь (г)
УЙ(Г)
к Ь-(г}гГ
к произведение век№ 69848 4 где b (г)- мнимая полуось гиперболоида с горловым кругом радиуса г. С помощью системы (II) четвертое уравиеиие (10) приводится к тождеству:
S - - S ( -Ж (12)
аг аг
где положено:
, Ь(г) - jb(r)r . , a (г) г
Ь(г)ЬЦг)гЦ . 1
/L /JГ/ 1Т)
Из тождества (12) следует
rf;„ d-i,
,, 2;:, .,: ::. 0.(14)
clrаг
Описа.нный выше вариант сопла соответствует случаю
:к 0, -1, 0, ,(15)
что в силу равенств (13) приводит к решениям:
г Ь(г} у , , , а(г) . const, „(г) 0.(16)
Уравнения (16) вместе с уравнениями (11) опреде.тяют поверхности -р const, реализующие поток по копгруэнции прямых.
П р е д, м е т и з о б р е т е и л я
Гиперболическое сопло, образованное двумя соосными одноиолостиыми гиперболоидами вращения, связанными между собой рядом направляющих линейчатых поверхностей, отличающееся, те.м, что асимптотические конусы граничпых гиперболоидов различны, причем, е целью реализовать течение газа переменного состояния по прямым линиям, задается определенная геометрия сопла, характеризуемая формулой:
tgy 1/ Сс---- - Г, ( г, .х,: г г, ).
где / Гз - радиусы горловых кругов граиичиых гиперболоидов;
г - кратчайщее расстояние образуюп ей линейчатой поверхности от оси сопла;
Т - угол этой образуюидей е осью сопла; к - произвольные постоянные; е - основание натуральных логарифмов.
b (г) b (г ) Н- г dRdR
dsдг
Фыг/



| название | год | авторы | номер документа |
|---|---|---|---|
| Цилиндрическое сопло | 1945 |
|
SU69871A1 |
| ТОКОСЪЕМНИК | 2002 |
|
RU2226309C1 |
| Прибор для демонстрации однополостного гиперболоида | 1987 |
|
SU1444865A1 |
| Инструмент для последовательной обкатки трубчатых заготовок | 1976 |
|
SU740355A1 |
| НАПРАВЛЯЮЩЕЕ УСТРОЙСТВО КАНАТОВ | 1997 |
|
RU2120911C1 |
| РОЛИКОВЫЙ ПОДШИПНИК КАЧЕНИЯ | 2014 |
|
RU2585437C2 |
| СПОСОБ ТОКАРНОЙ ОБРАБОТКИ ЦИЛИНДРИЧЕСКИХ ПОВЕРХНОСТЕЙ | 2005 |
|
RU2296035C2 |
| Зубчатая передача со скрещивающимися под прямым углом осями колес | 1973 |
|
SU533778A1 |
| Червячная передача | 1980 |
|
SU947531A1 |
| Двухконтурная система питания двигателя внутреннего сгорания газообразным топливом | 2019 |
|
RU2726424C1 |

S.
Авторы
Даты
1947-01-01—Публикация
1945-04-04—Подача