Известны цилиндрические сопла, ограниченные двумя соосными цилиндрами с направляющими лопатками, образующими систему вращения (т. е. каждая лопатка получается из любой другой лопатки путем поворота последней около оси сопла на некоторый угол).
Сопла такой конструкции применяются в осевых газовых турбинах, и компрессорах в качестве направляющих и трансформирующих аппаратов.
Предлагаемое цилиндрическое сопло отличается от известных формой своих направляющих лопаток, которая такова, что при достаточна больщом числе лопаток и надлежащем состоянии газового потока при подходе к краю лопаток поток внутри сопла будет близким к цилиндрическому и равномерному.
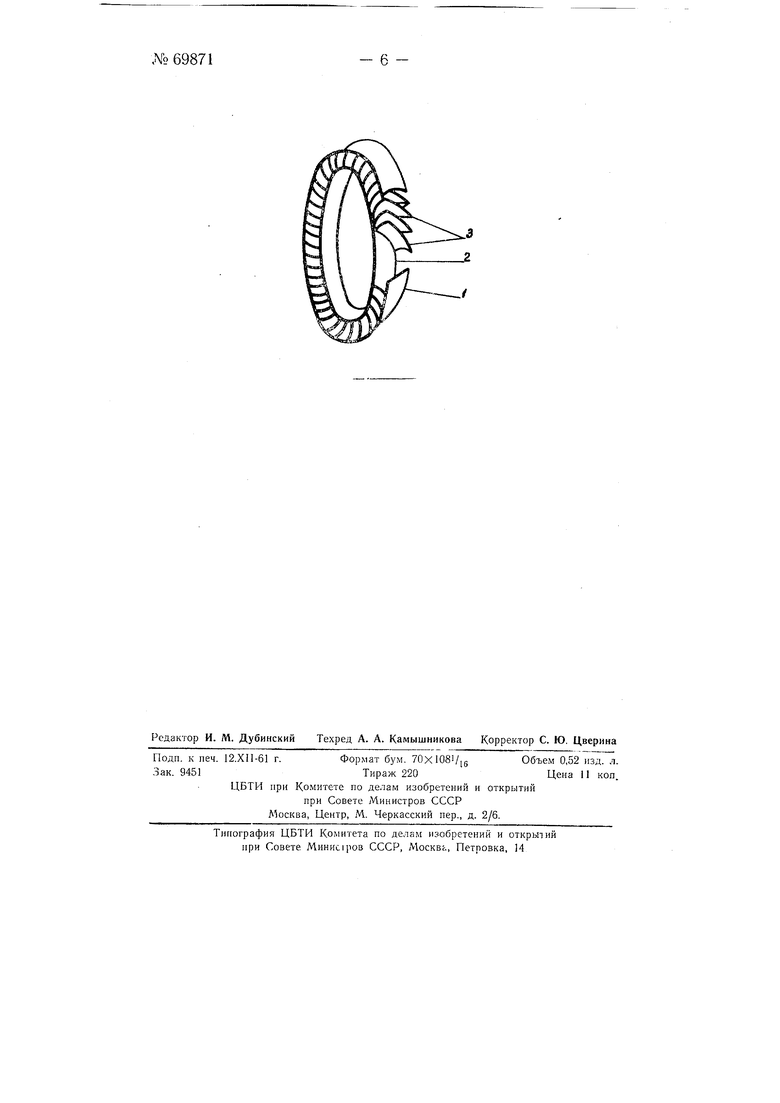
На чертеже схематично изображено предлагаемое сопло.
Основными частями цилиндрического сопла являются два соосных цилиндра / и 2 и направляющие лопатки 5.
Цилиндрическим потоком, из числа осесимметрических, называется; поток, в котором радиальная составляющая скорости равна нулю. Равномерный поток в рассматриваемом случае характеризуется тем свойством, что частицы газа, находивщиеся в некоторый момент времени в плоскости, ортогональной оси потока, остаются в этой плоскости все время, если сама плоскость движется вместе с потоком. Иными словами, абсцисса движущейся частицы является функцией только времени, если осью абсцисс считать ось потока. При этом условии плотность газа, а следовательно, и давление будут зависеть только от времени.
Если направляющую лопатку рассматривать как тонкую пластинку, т. е. как поверхность, то в предлагаемом сопле эта поверхность определяется в цилиндрических координатах г, ф, х и времени t следуюи ими уравнениями:
-. -У йМ-Г;(1)
2а 1 где р(/) является корнем уравнения
l, . Г- (Р,.„Г. (3)
В уравнениях (1), (2) и (3) принято: Ро Р ( 0) - начальное значение плотности газа;
-,T( -начальное значение осевой составляющей скорости потока, которое в предмете изобретения обозначено через а н b произвольные постоянные, определяющие начальный поток так, ч го
о -уг ( 0) - (начальная угловая скорость потока) -, ( 0)
( Ро
9 - скорость звука в начальном потоке; параметры
Z л х
п и Со являются параметрами уравнения состояния газа, которое предположено в виде
Р - Со о ,(4)
где р - давление газа.
Составляющие скорости потока для любого момента времени определяются в виде:
V ы -{-1
jc.- (осевая).(б)
Работоспособность сопла в идеальных условиях, т. е. для идеального газа с непрерывно распределенными бесконечно тонкими направляющими лопатками, обосновывается в результате рассмотрения дифференциальных уравнений потока со связями, образующими систему вращения.
Это обоснование следующее.
Пусть в const, есть уравнение непрерывного семейства гладких непересекающихся поверхностей, в присутствии которых соверщается поток идеального газа. Если указанные поверхности непроницаемы для газа, то они являются связями для потока, и, следовательно, при составлении уравнений движения газа необходимо учитывать реакцию этих связей на поток. Так как связи распределены непрерывно, то их реакция будет представлять объемную силу.
Постулируя непрерывность этой силы и осредняя ее для элементарного объема, как это делается всегда в задачах рассматриваемого типа, найдем, что уравнение Эйлера представится в виде
1, , , Д -.ргs;rad (/71 «и ,IО
VIо о
(2)
о
(тангенциальная);(.т)
где гт;р - производная вектора скорости w по вря мени;
р к р - плотность и давление газа;
К - коэффициент пропорциональности реакции связи; е - вектор нормали поверхности в const.
Пусть связи 0 const образуют систему вращения. Если поток, совершающийся в их присутствии, является цилиндрическим и равномерным, то конгруэнция линий тока может быть представлеиа в виде:
X x(
у-г. sir. 1 г (Л г) и j(8)
г :- r.(/,r) -:- Hj I
где к, у, Z - декартовы координаты пространства, в котором осью .v
является ось потока; t - время, а г и 0 - криволинейные полярные координаты
плоскости j: x(0). Для цилиндрических потоков уравнение неразрывности имеет вид:
Если - О, то из уравнений (9) и (4) следует, что
Тогда координатами grad (р) будут:
Считая поток стационарным, из уравнения (8) найдем координат1Л вектора -,,,, в виде:
х; ГУ cos (-г в) -r-p-sin(-f-г в): -ro-sin (cp-rB)-r9-cns (9 -;-«), (12)
где точки, поставленные сверху букв, означают дифференцирование по времени.
Из тех же уравнений найдем координаты вектора
зсэ г ср; ГХ - Sin ср :- Я - AT-COS ( - в):
r - -cos|9 в| . jc-sin(o-: в).(13)
Принимая во внимание уравнения (11), (12) и (13), представим уравнение (7) в координатной форме:
р X -- о„ л-„ .(9)
;0;(1(11)
зд:
X -, - r tp
X
Замечая, что 4- x - -- из уравнений (14), нолучим: dt ,,-,р.0
otp f
с/г Интегрируем но ф. Найдем:
г- -j-V {t)mr
I /-1
Я(г) -г 2C,
Считая начальный поток закрученным по закону Фо --.перепишем
уравнение (16) в виде:
1 dp k 1
о Й Л(j
(14)
k ifo - r.r -, 0Й r
I а/7 , , „
(15)
(i6i
х , 2а, - о первое уравнение (15) и результат решаем относитель





// (0.
где
Из условия совместности уравнения (17) и второго уравнения (15) следует:
Если не принимать во вкимаше решение Q О, реализуюш.ее поток с неизменяемыми параметрами по параллельным прямым, то будем иметь:
п I ,.
условий найдем:
г ) . t . - d
39У-г:02Й (18)
(19)
yc,t--c, (20)
- i(O)
Обозначая --vj-через b, получим
после чего из уравнения (17) следует
2я 1 ,.- р - . - Ybt
что и дает уравнение {), при в О.
Для определения и х служит система
р лг
( )--i(0) + a -р л: Ро д:„
, V.2 I 9Г А- 2С, -.- р Х() - Ь„ J г- м. , 0 J ;л. .
которая приводится к системе уравнений (2) и (3).
Предмет изобретения
Цилиндрическое сопло, состоящее из двух соосных граничных цилиндрических поверхностей, связанных между собой кривыми связями (направляющими лопатками), отличающееся тем, что, с целью создания равномерного и цилиндрического потока в сопле при условии заданного начального потока, направляющие лопатки выполняются в соответствии с уравнениями, написанными в цилиндрических координатах г, ф, X:
а ---- 1 hf 1- 1
h
Р., WX p(t) - корень уравнения:
рМОК i-2
причем РО й,гг| суть начальные значения плотности газа-р и осевой скорости потока X, а параметры а и 6 определяются но условиям натекания rioTOKa таким образом, что, если задана начальная угловая скорость потока
Од, то а -- , Ь --- - ( XX С, - , Y (Х
где Сз и п определяются из уравнения состояния р С,,р,
2Г
V bt , 1
1 в
122)
а
Ы
(rbt
9а
{ dt
Ы 1
Авторы
Даты
1947-01-01—Публикация
1945-10-31—Подача