(54) СИСТЕМА ИДЕНТИФИКАЦИИ


| название | год | авторы | номер документа |
|---|---|---|---|
| СТЕНД ДЛЯ ОПРЕДЕЛЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ НАВИГАЦИОННЫХ ДАТЧИКОВ | 1972 |
|
SU342198A1 |
| АДАПТИВНАЯ СИСТЕМА ДЛЯ ОБЪЕКТА С ЗАПАЗДЫВАНИЕМ | 2011 |
|
RU2482533C2 |
| Устройство для оценки статистических характеристки случайных процессов | 1974 |
|
SU515116A1 |
| СПОСОБ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КУРСОМ СУДНА И СИСТЕМА АВТОРУЛЕВОГО ДЛЯ РЕАЛИЗАЦИИ СПОСОБА | 2004 |
|
RU2282884C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ СОПРЯЖЕННЫХ КАНАЛОВ РЕГУЛИРОВАНИЯ РАСПРЕДЕЛЕННЫХ ОБЪЕКТОВ | 2006 |
|
RU2326422C1 |
| УСТРОЙСТВО ДЛЯ ОЦЕНКИ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ПРОЦЕССОВ | 1972 |
|
SU433495A1 |
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ АКТИВНОЙ МОЩНОСТЬЮ ГИДРОАГРЕГАТА С ПОВОРОТНО-ЛОПАСТНОЙ ТУРБИНОЙ | 2009 |
|
RU2468246C2 |
| Способ оперативной идентификации морских целей по их информационным полям на базе нейро-нечетких моделей | 2021 |
|
RU2763125C1 |
| УСТРОЙСТВО для СТАБИЛИЗАЦИИ СТАТИЧЕСКОГО КОЭФФИЦИЕНТА УСИЛЕНИЯ ДИНАМИЧЕСКОГО ЗВЕНА | 1969 |
|
SU247375A1 |
| Система оперативной идентификации морских целей по их информационным полям на базе нейро-нечетких моделей | 2021 |
|
RU2763384C1 |

I
Предлагаемая система относится к системам, вдентификации нелинейных объ1.ктов. Известны системы идентификации, содержащие модель объекта, объект, блок сравнения, вычислительное устройство и исполнительный механизм 1 и 2.
Из известных систем наиболее близкой к предлагаемой по технической сущности является система, содержащая модель объекта, первый вход которой соединен со входом объекта и первым выходом нормирующего блока, второй вход - с выходом исполнительного устройства, а выход - со вторым входом нормирующего блока, третий вход которого соединен с выходом объекта, а выход - со входом коррелятора, и блок сравнения, выход которого соединен со входом исполнительного устройства 3.
Существенным недостатком известной системы является ее низкая точность при идентификации нелинейных объектов, вызванная неоптимальностью математического описания процессов, протекающих в объектах.
Цель изобретения - повышение точности системы.
Поставленная цель достигается тем, что в ней установлены блок формирования весовых функций, блок формирования степенной корреляционной функции и блок формирования коэффициента разложения, первый вход которого соединен с выходом объекта, второй вход - с выходом модели объекта, третий вход - с вь ходом нормирующего блока, а вы10ход - с первым входом блока формирования весовых функций, второй вход которого через блок формирования степенной корреляционной функции соединен с выходом коррелятора, а выход - со входом блока сравнения.
15
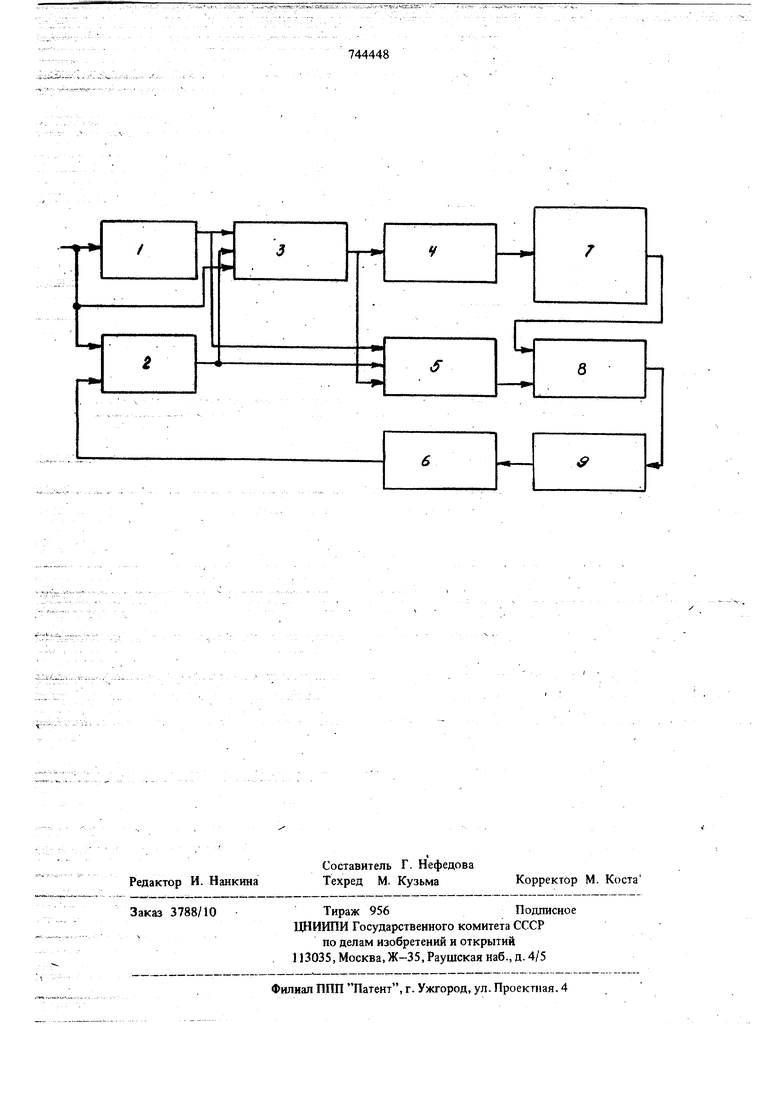
На, чертеже представлена блок-схема системы.
Система идентификации содержит объект 1, модель 2 объекта, нормирующий блок 3, коррелятор 4, блок 5 формирования коэффи20циентов разложения, исполнительное устройство 6, блок 7 формирювания степенной коррелящюнной функщш, блок 8 формирования весовых функций, блок 9 сравнения. Ичвестно, что оптимальным в статическом гсмысле (по критерию минимума ереднеквадратической ошибки) оператором в классе всех возможных операторов, описывающих преобразование динамической системой входного процесса X(S) в выходной процесс у Ш, является оператор условного математического ожидания, который может быть определен следующим оДра1ом Mly(t)|4S),aXx(t,S)H,x(S), (Д - коэффициенты ортогонального разложения регрессионной функции; Ax.s) -нормированная взаимная корреляционная функция; и rx(S)J -полиномы Чебышева-Эрмита; xCS) -нормированный входной процесс V(i) -цецтрированньш выходной процесс объекта управления. В соответствии с разложением условного математического ожидания идентифицируемБш объект (который в общем случае является .нелинейным) можно представить в виде совокупности параллельно соединенных подсистем, ядра преобразования которых выражаются через вторые моменты (t.3)i,(i)Hjx(S)J}j,;(t,s) Первая подсистема (п-1) осуществляет линейные преобразования, все последующие по системы (п 2, 3, ... К) описывают квадратичные, кубичные и т.д. преобразования исход ной системой входного случайного процесса. В задаче построения математической модел нелинейного объекта, определяющей его состо ние, важным моментом является оценка харак тера каждого из нелинейных преобразований (линейного, квадратичного, кубического и т.д Анализируя свойства полиномов ЧебышеваЭрмита, описываемых рекуррентной зависимостъюН.,«)Ц-И,()-пН(0 можно сделать вывод, что ядро первого поря ка f) не является общим линейным ядром объекта аналогично тому, как ядро h -го порядка (h 2, 3, ... |К) не является общим ядром п -го порядка объекта. С целью выде ления общих ядер преобразования аппроксими руют условное математическое ожидание полиномиальной регрессией M{y(t)K(S)J} Iok(t,S)y(S) n-i и, воспользовавшись общей формулой полино мов Чебышева-Эрмита )(y)(S)( где(| - сочетания из и элементов по , определим весовые функции .S) (S)-«npr/.s)-(2;vC(.sj Ч7, 7t,sj... Весовая функция G.,(i,S) характеризует инейную, (2(t,S) квадратичную, Aj(:,S) кубическую составляющие в выходном процессе идентифицируемого объекта. Таким образом, модель объекта, характеризующая его состояние, представлена в виде параллельного соединения К-подсистем. Точность такого представления (степенъ изоморфности модели) может быть оценена отношением дисперсий выходных процессов объекта У(1) и его модели )м{у((5)} . ) ЯнчГс7 (s)}, о« 8) Очевидно, что необходимая точность идентификации может быть достигнута изменением числа членов разложения К. Знание весовых функций разложения и дисперсий степеней входного сигнала объекта управления позволяют взвещивать влияние каждой составляющей разложения на степень изоморфности модели объекту управления. Оценка параметров объекта управления проводится путем сравнения одноименных весовых функшш объекта управления 5.(l,S) и его модели cA(-t,S) (функций одинакового индекса п ) и подстройки параметров модели с использованием регрессионных функции чувствительности до совпадения весовых функций объекта и модели. Система работает следующим образом. Входной сигнал поступает одновременно на объект 1 управления, модель 2 объекта и нормирующий блок 3. С выходов объекта 1 и модели 2 объекта сигнал поступает на два других входа нормирующего блока 3. Нормирующий блок 3 осуществляет центрирование реализаций относительно их математических ожиданий и нормирование относительно среднеквадратических отклонений процессов. Система имеет три цикла работы вычисление (формирование) весовых функ И rtf,(i,S); вычисление (формирование) весовых функций сл;|(1,6); определение состояния и параметров (бъек та 1. : Первые два цикла работы идентичны. При вычислении функций (t,S) на коррелятор поступают нормализованные входной сигнал и выходной сигнал объекта управления, а на входы блока 5 формирования коэффициентов разложения поступают нормализованный входной сигнал и выходной сигнал объекта 1. При оценке функции cX(i,Sj на коррелятор 4 поступают нормализованные входной и выходной сигналы модели 2 объекта, а на выходь блока 5 формирования коэффициентов разложения поступают нормализованный входной и выходной сигналы модели 2 объекта. В первом цикле работы коррелятор 4, например, путем аппроксимации корреляционной функции суммой членов разложения ее в ряд вычисляет нормированную взаимную корреляционную функцию ) результаты вычислений поступают в блок 7 формирования степеней корреляционной функции, вычисляющий оценки Puv4t,S)i - 1, 2,.. Блок 6 формирования коэффициентов разло жения оценивает коэффициенты ортогонального разложения регрессионной функции путем усре нения по времени произведений реализаций вы ходного сигнала объекта регулирования и выходных сигналов ортогонального фильтра. Результирующие сигналы, пропорциональные степеням нормированной взаимной корреляционной функции и коэффициентам ортогональ ного разложения регрессионной функции поступают в блок 5 формирования весовых функций который путем перемножения соответствующих сигналов и взвешивания в соответствии с представленным алгоритмом оценивает весовые функции C(t,8), которые определяют состояние объекта 1. Вычисленные в первом и втором циклах функции 0(t,S) и r(t,S) поступают в блок 9 сравнения и при несоответствии одноименных весовых функций исполнительным уст ройством 6 с учетом коэффициентов чувствительности весовых функций к вариациям параметров формируются управляющие воздействия на модель 2 объекта, осуществляется перестрой ка модели 2 объекта и производится оценка параметров объекта 1 (параметрическая идентификация объекта регулирования).i Таким образом, введение в систему блока формирования коэффициентов разложения, блока формирования степенной корреляционной функции и блока формирования весовых функций и описанное их соединение с известными блоками системы повышает ее точность. Формула изобретения Система идентификации, содержащая модель объекта, первьш вход которой соединен со входом объекта и первым выходом нормирующего блока, второй вход - с выходом исполнительного устройства, а выход - со вторым входом нормирующего блока, третий вход которого соединен с выходом объекта, а выход - со входом коррелятора, и блок сравнения, выход которого соединен со входом исполнительного устройства, отличающаяся тем, что, с целью повыщения точности системы, в ней установлены блок формирования весовых функций, и блок формирования степенной корреляционной функции и блок формирования коэффициента разложения, первый вход которого соединен с выходом объекта, второй вход - с выходом модели объекта, третий вход - с выходом нормирующего блока, а выход - с первым входом блока формирования весовых функций, второй вход которого Через блок формирования степенной корреляционной функции соединен с выходом коррелятора, а выход - со входом блока сравнения. Источники информации, принятые во внимание при экспертизе 1.Теория автоматического регулирования. Под. ред. Солодовникова В. В., книга 2, М., Мащйностроение, 1967, с. 93-143. 2.Самонастраивающая система. Справочник под ред. Чинаева ПИ Киев, Наукова думка, 1969, с. 410-440. 3.Уланов Г. М. Динамическая точность и компенсация возмущений в системах автоматического управлений. М., Мащиностроение, 1971, с. 106-107 (прототип).
Г
Авторы
Даты
1980-06-30—Публикация
1975-08-01—Подача