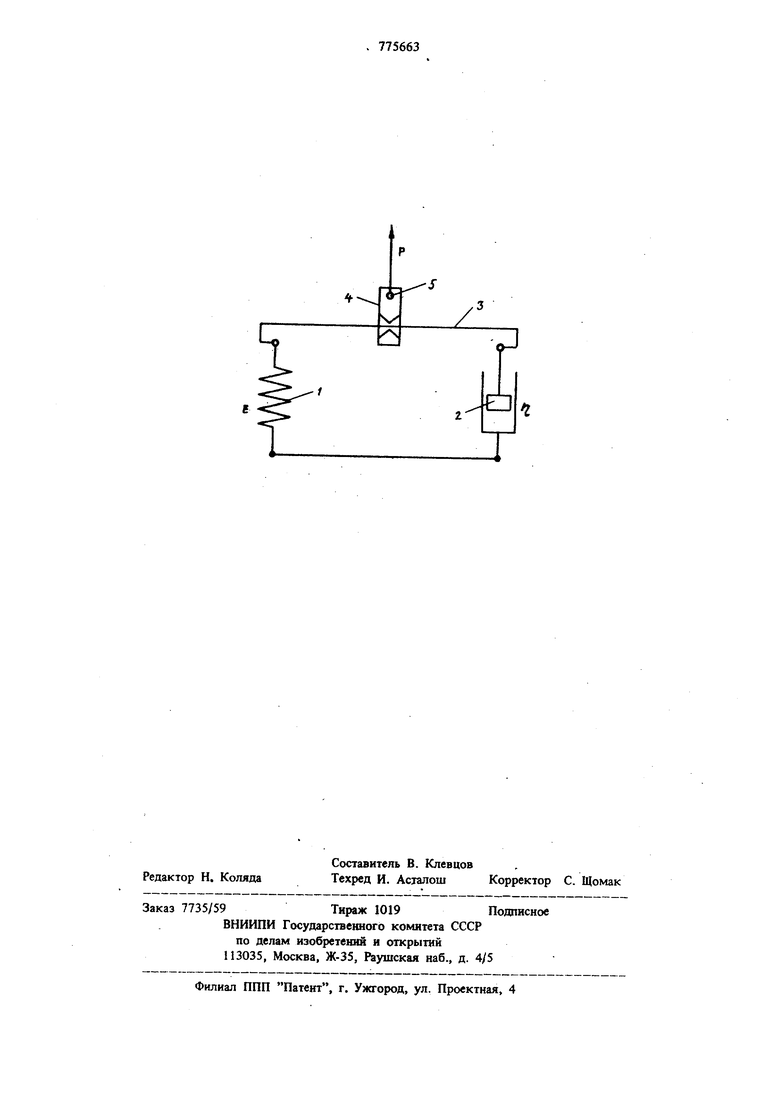
Изобретение относится к средствам моделирования физико-механических свойств вязкоупругих сред и может быть применено для изучения свойств биологических жидкостей, свойства которых изменяются во времени вследствие ферментативных реакций : В частности, пред лагаемая модель может использоваться в качест ве модели свертывающейся крови. Известна механическая модель вязкоупругого тела, включающая параллельно соединеннь1е модели вязкого и упругого тел, злемент приложения напряжения сдвига 1 . Модель исполь зуется для исследования физико-механических свойств вязкоупругих сред - органических гелеобразных соединений. Недостатком известной модели является непригодность ее в качестве модели тел, свойства которых изменяются во времени от вязких к упругим, т.е. при перераспределении соотношения этих свойств, как, например, в процессе .свертывания крови. Кровь в результате протекающих в ней ферментативных реакций претерпевает изменение реологических свойств от вязких свойств жидкой крови (суспензия: дисперсионная среда - плазма, дисперсионная среда, дисперсная фаза - форменные злементы) к упругим свойствам фибриноцитарной структуры сгустка (объемная зластичная структура полимера тромбина). Промежуточная фаза свертывания характеризуется гелеобразным состоянием, в котором проявляются и вязкие, и упругие деформационные свойства с переменным соотношением. Таким образом, известная модель (модель Кальвина) может имитировать поведение свертывающейся крови в промежуточной фазе свертывания, но не моделирует начальных и конечных свойств крови. Кроме того, модель Кальвина не отражает динамики перехода свойств, что весьма важно при исследовании свертываемости крови в условиях невоспроизводимости опыта, например, in virto, невозмож ность остановить п{ оцесс свертывания на интересующей стадии подтверждает необходимость модели для исследования физико-механических свойств крови. Цель изобретения - обеспечение воз.можности изучения структурно-механических свойств неоднородных систем с перераспределяющимися во времени вязкими и упругими свойствами. С этой целью вязкий и упругий элементы связаны соединяющей их траверсой тарнирно на траверсе установлен с возможностью возвратно-поступательного перемещения по ней пол зун, снабженный шарниром. Благодаря предложенной конструкции механическая модель позволяет изучать физико-меха нические свойства свертывающейся крови, моде лируя ее на любой стадии свертывания путем перемещения точки приложения напряжения сдв га между упругими и вязкими элементами. На чертеже изображена кинематическая схема предлагаемой механической модели вязкоупругого тела. Моделирующая упругое тело пружина 1 и поршневая пара 2, которая моделирует вязкую среду, являются элементами, составляющими противоположные звенья замкнутого четырехзвешшка. Соединяющая упругий элемент I и вязкий эле.мент 2 со стороны приложения напря жения Р сдвига траверса 3 сочленена с элементами 1 и 2 шарнирами, а на траверсе подвижно укреплен ползун 4. Ползун 4 снабжен шарниром 5, который является элементом приложе ния напряжения Р сдвига. Работу модели рассмотрим на примере иссле процесса свертывания, когда исходные данные для моделирования в результате испытаний крови в коагулометре и тромбо эпастометре. На основании измеренных начальной вязкости пробы (по показателю гематокри та в коагулометре) и максимальной прочности сгустка (по максимальной упругости и тромбоэластометре) устанавливают соответствующие значения вязкоста т для вязкого элемента 2 и упругости Е для упругого элемента 1 (использованная проба крови не восстанавливается и условия свертывания в натуре не воспроизво ,аятся). Действия с моделью начинают с исходного положения ползуна 4, когда направление напря жения Р совпадает с осью элемента 2 (т.е. крайнее правое положение). В этом положении плечо между напряжением Р и вертикальной осью элемента 2 равно нулю, а плечо между Р и осью упругога элемента 1 равно длине . траверсы 3 - , Поэтому действие Р будет направлено на деформащ1ю вязкого звена 2 и поведение модели, ее деформационные свойства подвдняются закону Ньютона: где - скорость деформации. При перемещении ползуна 4 влево длина траверсы 3 делится им на два плеча, через которые напряжение Р передается элементам 2 1 пропорционально соотношению плеч. В фикированном промежточном положении ползуна еформа1-даонные свойства модели описываются равнением вязкоупругого тела Кельвина; dS , де , - величина деформации. В левом крайнем положении ползуна 4 - при совпадении направления Р с осью пружины 1 - работает только звено упругости и модель представляет собой упругое тело, описываемое законом Гука: Р ЕЁ. При непрерывном перемещении ползуна для моделирования непрерывного процесса свертывания окончательное уравнение модели примет вид: dC k - текущее значение плеча от направления действия Р до оси вязкого элемента 2. Моделирование свертывания крови в динамике при возмушаюших воздействиях x(t) и противодействующих регулирующих воздействиях х (t) осуществляют перемещением ползуна по закону k (t) + x(t). Таким образом, предложенная модель позволяет исследовать процесс свертывания крови как в динамике при переходе состояния тела от жидкого к упругому через гелеобразное, так и при заданном соотношении вязких и упругих свойств в статике, как. бы в остановленном на интересующей стадии процесса. Формула изобретения Механическая модель вязкоупругого тела, включающая параллельно соединенные траверсой модели вязкого и упругого тел, элемент приложения напряжения сдвига, отлича.ющая с я тем, что, с целью обеспечения возможности изучения структурно-механических СВОЙСТЕ неоднородных систем с перераспределяющимися во времени вязкими и упругими свойствами, вязкий и упругий элементы связаны с соединяющей их траверсой шарнирно, а на траверсе установлен с возможностью возвратно-поступательного перемещения по ней ползун, снабженный шарниром. Источники информации,, принятые во внимание при экспертизе 1. Kelvin W. Elasticity Encyclopedia Britannica, 9th et London, 1875, p. 371 (прототип).
-,S

| название | год | авторы | номер документа |
|---|---|---|---|
| Модель вязкоупругого тела | 1978 |
|
SU777669A1 |
| СПОСОБ МОДЕЛИРОВАНИЯ ХРОНИЧЕСКОЙ ТОКСИЧЕСКОЙ КОАГУЛОПАТИИ У КРЫС | 2023 |
|
RU2800860C1 |
| СПОСОБ ПОЛУЧЕНИЯ ЭЛЕКТРОРЕОЛОГИЧЕСКИХ СУСПЕНЗИЙ | 2012 |
|
RU2499030C1 |
| Способ моделирования нарушений коагуляционного звена системы гемостаза | 2019 |
|
RU2714597C1 |
| Способ моделирования нарушений гемостаза при сочетанном поражении легких бактериальным воспалением и тромбозом легочных сосудов | 2023 |
|
RU2800645C1 |
| Устройство для измерения сдвиговой вязкости и упругости сред | 1976 |
|
SU682796A1 |
| Устройство для моделирования сложного напряженного состояния горных пород | 1988 |
|
SU1615361A1 |
| Устройство для моделирования реологических характеристик материалов | 1989 |
|
SU1700444A1 |
| СПОСОБ МОДЕЛИРОВАНИЯ ХРОНИЧЕСКОЙ ТОКСИЧЕСКОЙ КОАГУЛОПАТИИ У КРЫС В ЭКСПЕРИМЕНТЕ | 2022 |
|
RU2785847C1 |
| Способ профилактики хронической токсической коагулопатии у экспериментальных животных | 2018 |
|
RU2683723C1 |

О
Авторы
Даты
1980-10-30—Публикация
1976-03-29—Подача