Предлагается зубчатый планетарный редуктор с некруглыми шестернями, например, для осуществления переменной по величине и направлению скорости вращения ведомого звена при постоянной скорости вращения ведущего звена.
Предлагаемый планетарный редуктор отличается от известных тем, что все его шестерни выполнены некруглыми. Такой редуктор позволяет осуществлять переменное передаточное отнощение, закон изменения которого выражается функцией, имеющей в воспроизводимом интервале положительные, отрицательные, а также экстремальные значения.
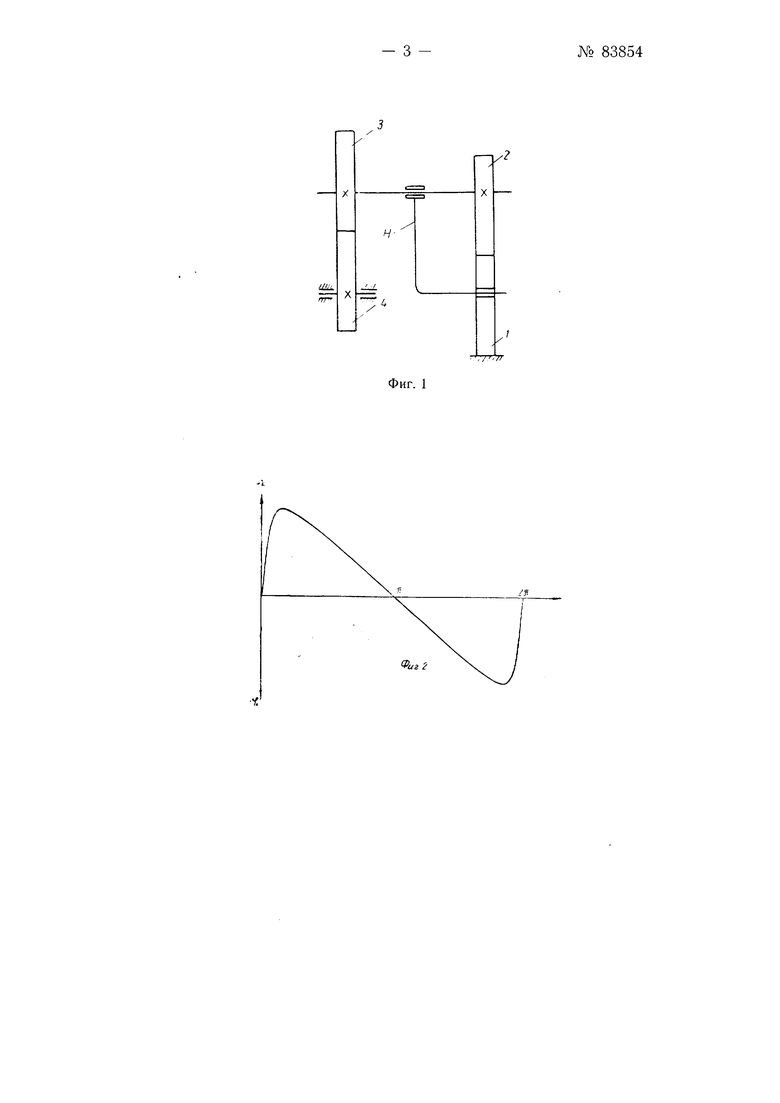
На фиг. 1 показана кинематическая с.хема редуктора; на фиг. 2- график закона изменения передаточного отношения для редуктора с эллиптическими шестернями.
Редуктор может быть выполнен, например, по схеме механизма Давида с двумя парами некруглых шестерен, как зто показано на фиг. 1. Ведущим звеном редуктора является водило Н, промежуточными звеньями-некруглые шестерни /, 5 и 5 и веДомым звеном-некруглая шестерня 4.
Зависимость между углами поворота шестерни 4 и водила может быть в этом случае определена из формзлы:
Ф4 /(фч)-Ф„, где ф4 - угол поворота шестерни 4;
Ф„ - угол поворота водила.
Функция F((fi) выражает зависимость между углами поворота Шестерен 4 и 1, рассматривая ряд щестерен /-4, как простой.
Угол ф« ф1, где ф1 - угол поворота шестерни / в простом ряду. Для определения угла ф4 по функции f (фО следует произвести расчет по такой схеме:
причем фз ф2ф4 /1(фз),
№ 83854- 2 Эта зависимость определяется выбранными очертаниями центроид шестерен 5 и 4. В свою очередь, между углами поворота шестерен 2 и / сушествует зависимость, определяемая центро/1дами шестерен 2 и /, т. е.
Фз Ф2 Fi(f).
Следовательно, задаваясь углом cpi, можно найти угол поворота ф2 Фз, а затем значение ., , соответствуюшее определенному значению Фз.
Пусть в планетарном редукторе применены две одинаковые пары эллиптических шестерен с эксцентриситетом е.
Зависимость между углами поворота первой пары эллиптических шестерен выражается следующим уравнением:
-2arctg(.-)
-.(1 .- /)tg.
Соответственно зависимость между углами поворота второй пары некруглых шестерен выразится уравнением:
(1 --/}to-|-(l-r/)tgj.
Зависимость между углами поворота шестерен 4 н J, рассматривая ряд шестерен 4-/, как простой, выразится уравнением:
...rcl.(iiiyte|
Зависимость между углами поворота шестерни 4 и водила Я планетарного редуктора выразится уравнением:
-te (и). -,.
При / 0,6 эту зависимость графически можно нредставить кривой, изображенной на фиг. 2. Из этой фигуры видно, что функция имеет значения как в полож ительной, так и в отрицательной областях и в заданном интервале имеет экстремальные значения.
Предмет изобретения
Зубчатый планетарный редуктор, о т л и ч а ю ш, и и с я тем, что для осуш.ествлеЕ1-ия переменного передаточного отношения, закон изменения которого выражается функцией, имеющей в воснроизводимом интервале положительные, отрицательные, а также экстремальные значения, вес шестерни редуктора выполнены в виде некруглых шестерен.
1 f 

| название | год | авторы | номер документа |
|---|---|---|---|
| Способ проверки центроид некруглых зубчатых колес | 1949 |
|
SU88033A1 |
| СПОСОБ ОБРАБОТКИ НЕКРУГЛЫХ ПОВЕРХНОСТЕЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2002 |
|
RU2214889C1 |
| ТРАНСМИССИЯ ПЛАВАЮЩЕГО ТРАНСПОРТНОГО СРЕДСТВА | 2003 |
|
RU2243109C2 |
| ОБЪЕМНАЯ ГИДРОМЕХАНИЧЕСКАЯ ПЕРЕДАЧА | 2004 |
|
RU2269707C1 |
| Механизм швейной каретки ниткошвейной машины | 1989 |
|
SU1777586A3 |
| Безэксцентриковое универсальное мотовило | 1987 |
|
SU1477304A1 |
| Бурильная машина | 2002 |
|
RU2224076C1 |
| МЕХАНИЗМ ДЛЯ ПРЕОБРАЗОВАНИЯ ДВИЖЕНИЯ | 1995 |
|
RU2102642C1 |
| Импульсивный планетарный редуктор | 1960 |
|
SU134532A1 |
| МЕХАНИЗМ БЛОКИРОВКИ ДИФФЕРЕНЦИАЛА ТРАНСПОРТНОГО СРЕДСТВА (ВАРИАНТЫ) | 1995 |
|
RU2091249C1 |


Авторы
Даты
1950-01-01—Публикация
1949-01-19—Подача