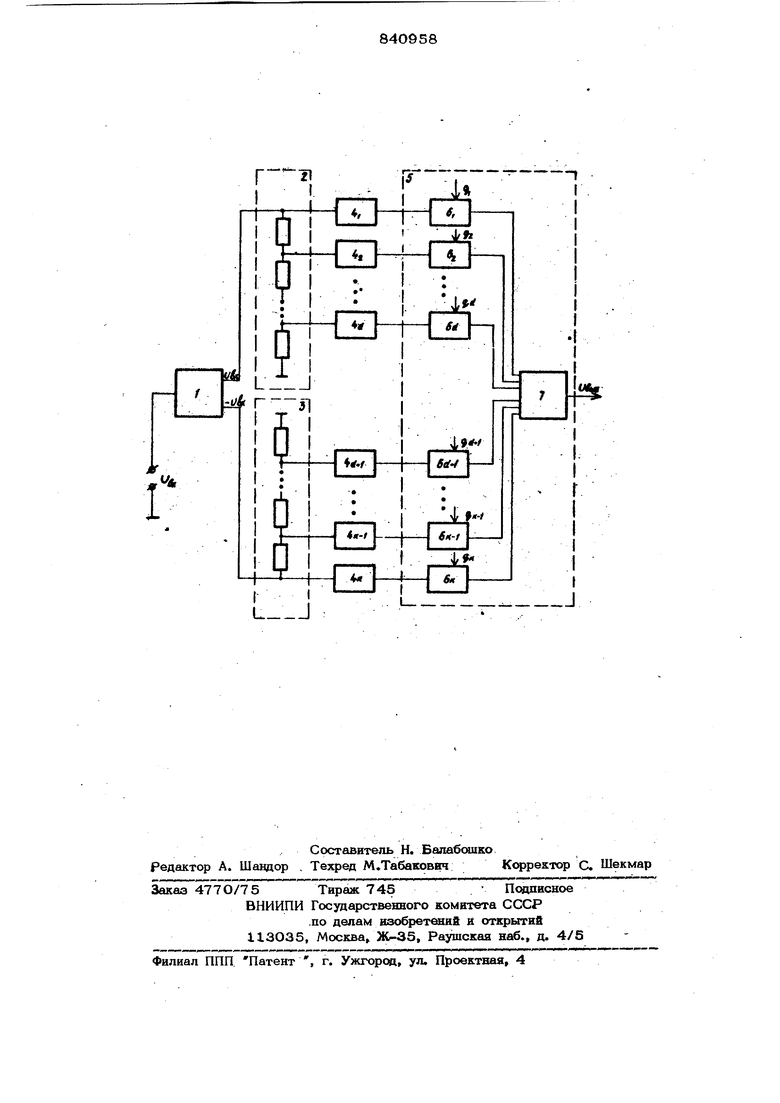
(54) ФУНКЦИОНАЛЬНЫЙ ПРЕСВРАЗОВАТЕЛЬ Цель достигается тем, что функциональный преобразователь, содержащий делитель напряжения, К блоков полиномиального пресбразования, сумматор,. выход которого является выходом функционального преобразователя, а входы соединены с выходами соответствующих блоков полиномиального гфеобразования, входы первых d блоков пояиномиальногр Преобразования соединены с соответствую щими выходами делителя напряжения, дополнительно содержит ларафазный входной усилитель и дополнительный делитель напряжения, выходы которого соединены со входами K-d блоков полинрмиальнсяр,о) Едреобразования, вход парафаэного входного усилителя является входом преобразователя, а первый и второй выходы соединены соответственно со входом основного делителя напряжения и со входом дополнительно1хэ делителя напряженияНа чертеже приведена блок-схема функционального преобразователя. Преобразователь содержит парафазный усилитель 1, основной 2 и дополнитель ный 3 делители напряжения, К блоков номйального преобразования 4,,., 4 -, сумматор 5, реализованный на элементах 6,... ,6|, задания коэффициента и суммирующем усилителе 7. Преобразователь работает следующим образом. При подаче на вход напряжения 11, на первом и втором выходах парафазного усилителя 1 формируются напряжения}Ug и-Uftx. На входах блоков полиномиального преоб зования 4,.,., 4 формируются напряжений, :функционалы}© связанные с , а именно, являющиеся полиномами степени m, где m К, от напряжения Ug,x . которые, oднaкoJ все различны в силу того, чти входное напряжение U,j поступает на входы блоков 4, ,4 со своим коэффициентом передачи, определяемым делителями 2 и 3 напряжения. На входе сумматора 5, если все весовые коэффициенть с , (2 , .... ,, с которыми суммируются выходные напряжения блоко 4, 4,,..., 4 , .выбраны правильно, получим напряжение U..., , которое связано ЬЫХ, с входным напряжением требуемой полиномиальной зависимостью .-51 Ь L ti Проанализировав работу преобразователя, можно определить способ вычисЛения коэффициентов (, С, , обеспечивающих реализацию требуемой функции, для удобства анализа полагая К т . Пусть на входы блоков 4., 4ij, ...,4ц поступают с выходов делителя 2 напряжения (i l,2,...,d), a с выходов делителя 3 напряжения Uj,xi (ч d +1, ... , К). Учитывая, что все блоки 4, ...,4 Of HHaKOB i, полином , а а U biitr , k , на выходе каждого из них имеем соответственно йыхх- т 1 вх: т 2 вх.- ш Полученные выражения можно рассматривать как систему лннейных уравнений с неизвестными К Ug,y , К,, , ... Эта система имеет всегда единственное решение, так как определитель системы является О15}еделителем Вандермонда, который отличен от нуля. Известно также что , П , (С:-С-) .mJ Рещение систем может быть получено с помощью формул Крамера - .т и -JL L U. где - определитель той же матрицы, у которой,однако, -и столбец заменен толбцом из , Ubt,,# , ..., UftbK.KРазложив правую часть формулы Крамера по элементам i -го cтoлбцa получим m &-«-t М 2- (ч) -д U , (л д & ае М -минор элемента С j (в даном случае-E|J J определителя Д , т.е. . пределитель порядка т-1, полученный з Д вычеркиванием -ой строки и t -го толбца. Таким образом, функциональное преобазование возведения в л -ю степень может быть реализовано путем весового суммирования выходов всех блоков полино 1иального преобразования 4 , , ... 4, с весамк, определяемыми коэффициентам при Ивых в сумме (2). От блоков 4 , ... 4ц при этом требуется, чтобы коэффициент KL полинома, описывающего их характеристику, был отличен от нуля Требуемая функция, описываемая зада ным полиномом степени п , может быть попущена tiyreM линейной комбинации выходных каналов всех блоков 4 , ... 4 т.е. их весового сумм фовадиа. Испольву полученное выражение (2), можно записать (.и и -TV, и-г-2 т («л Bb,4:,V K;|:/) fl. .еr-iH/ .; 6ых.6 1 ПТаким образом, требуемая функция может быть воспроизведена при суммировании выходных напряжений всех К блоков 4, , ... ,4 соответственно с вес выми коэффициентами : Из выражения (З) видно, что если какой-либо коэффициент полинома равен нулю, то при этом и в полиноме, аппрок симирующем хщ)актеристику одного из блоков 4( , ...,4ц. допустимо иметь К О. Значения коэффициентов апгфоксимирующего полинома К; могут быть неиз вестны. В этом случае необходимо экспериментально О1феделить известными методами коэффициенты полинома, аппрок С1фующего заданную функцию. .В предлагаемом щюобр азрвателе точность достигается следукицнм образом. .../г Из выражений (3) и (4) напряжение на , выходе функционального преобразователя может быть представлено в виде ftbK-..V ВЫЧ.8 где весовые коэффициенты а. являются константами, которые рассчитываются, исходя из номинальных значений величин . J К и 0 . При этом величины fej, известны точно, а К могут быть доста точно точно определены из математического описания характеристики блоков , ... , 4) или измерены в результате идентификации. Поэтому наибольший интерес представляет учет погрешности эа счет отклонений коэффициентов С, от своих номинальных значений в результате технологических разбросов параметров делителей 2 и 3 . Последние приводят к соответствующим отклонениям насфяжений Uftwx. величины которых могут быть рассчитаны по формуле (I). В предложенном преобразователе эти отклонения значительно меньше по сравнению с аналогичными отклонениями у известного устройства при одинаковых требованиях и точности выполнения делителей 2 и 3. Покажем эго на примере конкретного гфеобразователя, осуществляющего умножения частоты входного сигнала в 4 patза, в котором с точностью до постоянной составляющей должно быть реализовано функциональное преобразование (к), т.е. полином Чебьш1ева 4-го псфядка. Предположим, что мы располагаем блоком полиномиального преобразования 4 , .... 4 с характеристикой, описывающейся полиномом 4-го пс ядка; 1 1,5 X - 1,2 0,9х . Сравним два преобразователя, реализующих преобразования -8 X + 8 X и вьшолненныХ) соответственно по схеме известного и схеме предлагае мого преобразователя При идеальном их выполнения спектр одного сигнала при вхсздном воздействии CO&U)Tt кроме постоянной составляющей должен содержать лишь одну отличную от нуля составляющую на частоте 4 U), равную IE). В известном устройстве коэффициенты делителей выбраны равными: С I:, С2 O,844;Cj 0,5О8;С4 О,127. Можно показать, что указанные величины 64 обеспечивают максимальную устойчивость работы прео шэователя по отношению к технологическим разбросам параметров делителя. Оря этом коэффи- f «f- -vv циенты, вычисленные в соответствии с выражением (4), равны: (1 32,6; % -134О; cj,, 1981; ( -1116. ;Пусть щ}и изменении номиналов С , Сп и Сл , например, за счет технологических разбросов параметров на 1% их величины фактически составляют: ,852; Cjj O,513;Cj О,128. Тогда, как показывают расчеты, спектр выходного сигнала составляет соответственно на частотах Ы -6,47Й; 2СО - 1,11Ь; Зы -l,36b;4u)- 0,79fe. Таким образом, погрешность делителя в 1 % известного 1Ц еобразователя оказывается недопустиМО болыиой, поскольку спектр его выходного сигнала содержит паразитные составляющие, в несколько раз превосходящие полезную .
В предлагаемом преобразователе коэф.фициенты делителя выбраны равными: С 1,О; Cf О,653;Са 0,653; CZ| 1,0. При этом коэффициенты имеют
значения С 5,27О; (2°-4,543; (-4,543, CJ,; 5,27О. Предположим, что в результате изменений отличных ог нуля номиналов .0 также на 1 % они Принимают значения: О,659;Сп, О,659, При этом спектр выходного сигнала составляет соответственно на чбстотах Ш - ОЬ J 2Ш-0,О15Ь ; 3ul-O6{ 4u) -О,993Ь ; т.е. наблюдается только одна паразитная составляющая на частоте 2 и), которая примерно,в 66 раз меньше основной. Кроме того, ,й предлагаемом преобразователе коэффициенты а, существенно меньше по абсолютным величинам соответствующих коэффициентов нэвесгного усгройсгва и отличаются друг от друга JB меньшее число раз.
Это существенно облегчает практическую реализацию предлагаемого преобразователя по сравнению с известным и приводит к повышению точности и снижению стоимости.,
Теоретически уменьшение чувствительности к разбросу параметров и связанное с 1НИМ повышение точности объясняется существенным улучшением обусловленности системы линейных уравнений (1), которая достигается при выборе коэффициентов D в диапазоне | -1, 1 в ,
предлагаемом преобразователе вместо их выбора в диапазоне у известного.
Формула изобретения
Функциональный преобразователь, содержащий делитель напряжения К блоков полиномиального преобразования, , сумматор, выход которого являете выходом функционального преобразователя, а входы соединены с выходами соогвегсгвующих блоков полиномиального тфесфазования, входы первых d блоков полиномиального преобразования соединены с соответствуюишми выходами делителя напряжения,. отличающийся тем, что, с целью повьпиения точности, он содержит парафазный .входной усилитель и дополнительный делитель напряжения, выходы которого соединены со входами K-d блоков полиномиальн1эго гфеобразования, вход парафазного входного усилителя является входом преобразователя, а первый и второй выходы соединелй соответственно со входом основного делигеля напряжения и со входом дополнительного делителя напряжения.
Источники инфсрмаиии, принятые во внимание ори экспертизе
1.Авторское свидетельство СССР № 98714, кл. Q O6Gf 7/26, 1957.
2.Авторское свидетельство СССР № 598О58, кл. GI 06& 7/26, 1976.
.J :



| название | год | авторы | номер документа |
|---|---|---|---|
| Регистр сдвига | 2017 |
|
RU2691852C2 |
| СПОСОБ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ | 2014 |
|
RU2541905C1 |
| Устройство для сжатия данных | 1987 |
|
SU1522268A1 |
| СПОСОБ АДАПТИВНОЙ КОМПЕНСАЦИИ ВЛИЯНИЯ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ МОМЕНТА НАГРУЗКИ В ЭЛЕКТРОМЕХАНИЧЕСКОЙ СИСТЕМЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2565490C1 |
| Устройство для линеаризации характеристик измерительных преобразователей | 1976 |
|
SU593223A1 |
| СПОСОБ И УСТРОЙСТВО КОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК | 2007 |
|
RU2408979C2 |
| УСТРОЙСТВО ДЛЯ УСТРАНЕНИЯ ВЛИЯНИЯ ГАРМОНИЧЕСКИХ ВОЗМУЩЕНИЙ МОМЕНТА НАГРУЗКИ В ЭЛЕКТРОМЕХАНИЧЕСКОЙ СИСТЕМЕ | 2016 |
|
RU2650341C1 |
| Способ диагностики недвоичных блоковых кодов | 2018 |
|
RU2693190C1 |
| Широтно-импульсный функциональный преобразователь | 1981 |
|
SU993289A1 |
| Устройство для воспроизведения дробно-рациональных функций | 1983 |
|
SU1151999A1 |


Авторы
Даты
1981-06-23—Публикация
1979-10-12—Подача