Область техники, к которой относится изобретение
Настоящее изобретение относится к способу и устройству блочного кодирования с исправлением ошибок для разделения информационной последовательности на блоки определенной длины и независимое добавление избыточной последовательности к каждому из блоков, более конкретно к способу и устройству для кодирования с проверкой на четность (LDPC) с низкой плотностью.
Уровень техники
Системы связи, например, системы спутниковой или мобильной связи, включают в себя технологию исправления ошибок с большой эффективностью кодирования для выполнения системных требований для снижения мощности и малого размера антенны. Код с проверкой на четность с низкой плотностью известен как код с исправлением ошибок, который имеет очень высокую эффективность кодирования. Внедрение кода с проверкой на четность с низкой плотностью в различных системах связи и устройствах хранения данных, например магнитных устройствах хранения данных, в настоящее время развивается.
Схема кодирования с проверкой на четность с низкой плотностью не ссылается на одиночную схему кодирования исправления ошибок, но ссылается на общий термин для кодов исправления ошибок, которые характеризуются тем, что они определяются разреженной проверочной матрицей. Разреженная проверочная матрица означает, что большинство компонентов (элементов) проверочной матрицы равны "0", и число компонентов "1" очень мало. Как раскрыто в публикации D.J.C. Mackay, "Good Error-Correcting Codes Based on very sparse matrices" («Хорошие коды с исправлением ошибок на основе очень разреженных матриц»), протоколы IEEE по теории информации, стр.399-431, март 1999 г. (непатентная литература 1), кодирование с проверкой на четность с низкой плотностью характеризуется тем, что оно может предоставить схему кодирования с исправлением ошибок, которая имеет очень высокую эффективность кодирования, близкую к теоретически ограниченной, с помощью использования повторной схемы декодирования, например алгоритма суммы-произведения на основе выбора разреженной проверочной матрицы.
Одной технической проблемой для кода проверки на четность с низкой плотностью является то, что он требует большого объема вычислений для процесса кодирования, т.е. процесса вычисления избыточной битовой последовательности из информационной битовой последовательности. В наиболее характерном устройстве кодирования, где формирование избыточной битовой последовательности содержит вычисление умножения матриц на матрицу формирования кодов, формирование кодовой последовательности с проверкой на четность с низкой плотностью требует множества операций исключающего ИЛИ, которое пропорционально второй степени длины кода.
Если устройство кодирования содержит матрицу проверки кода, тогда проверочная матрица первоначально преобразовывается из условия, что часть проверочной матрицы становится диагональной матрицей, как показано с помощью уравнения (1), и формирование кодовой последовательности с проверкой на четность с низкой плотностью осуществляется с помощью первоначально преобразованной проверочной матрицы.
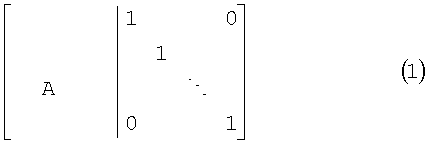
В частности, если предполагается, что r и k представляют собой положительные целые числа, i - целое число в интервале 1≤i≤r, А в уравнении (1) - матрицу r×k, и c1, c2, …, ck - информационную битовую последовательность из k битов, тогда каждый бит pi соответствующей избыточной битовой последовательности p1, p2, …, pr вычисляется согласно следующему уравнению (2):
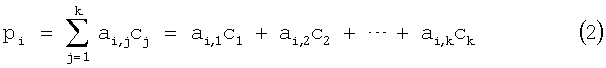
где j представляет собой целое число в интервале 1≤j≤k, и ai,j - компонента (i,j) матрицы А r×k. Для того чтобы осуществить кодирование кода с исправлением ошибок, необходимо сохранить матрицу А r×k в запоминающем устройстве, например в памяти, и выполнить количество операций исключающего ИЛИ, равное количеству значений «1» в компонентах матрицы А.
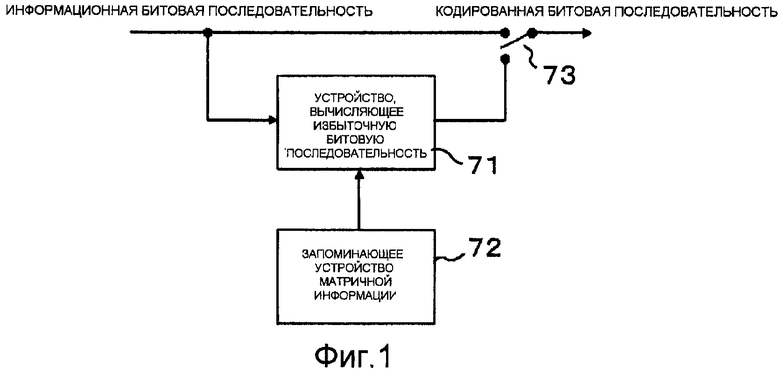
Фиг.1 показывает пример конфигурации устройства кодирования согласно уровню техники для осуществления кодирования с помощью кода с проверкой на четность с низкой плотностью. Когда проиллюстрированному устройству кодирования задана информационная битовая последовательность, оно кодирует информационную битовую последовательность с кодом проверки на четность с низкой плотностью и выводит кодовую битовую последовательность. Устройство кодирования содержит устройство 11, вычисляющее избыточную битовую последовательность для осуществления вычисления согласно уравнению (2) по информационной битовой последовательности для формирования избыточной битовой последовательности, запоминающее устройство 72 матричной информации для сохранения матрицы А, показанной в уравнении (1) и предоставления компонентов (элементов) матрицы А устройству 71, вычисляющему избыточную битовую последовательность и переключатель 73, для поочередного выбора информационной битовой последовательности и избыточной битовой последовательности из устройства 71, вычисляющего избыточную битовую последовательность, для формирования, таким образом, кодовой битовой последовательности, которая содержит комбинацию информационной битовой последовательности и избыточной битовой последовательности. Устройство 71, вычисляющее избыточную битовую последовательность, включает в себя схемы исключающего ИЛИ.
Для уменьшения емкости памяти запоминающего устройства (т.е. запоминающее устройство 72 матричной информации) и снижения числа схем исключающего ИЛИ, включенных в устройство 71 вычисления избыточной битовой последовательности, известен процесс создания кода с проверкой на четность с низкой плотностью из условия, что число "1" в компонентах матрицы А настолько мало, насколько возможно, и эффективность кодирования, достигаемая с помощью повторного декодирования, является предпочтительно большей. Такой процесс создания раскрыт, например, в публикации Томаса Ричардсона, Р.Урбанке "Efficient Encoding of Low-Density Parity-Check Codes" ("эффективное кодирования кодов с проверкой на четность с низкой плотностью"), протоколы IEEE по информационной теории, стр.619-656, сентябрь 2001 г. (непатентная литература 2). JP-2003-115768A (патентная литература 1) и JP-2004-72130A (патентная литература 2) раскрывают процесс использования матрицы, содержащей блочные матрицы из матрицы циклических перестановок как проверочной матрицы и ограничивающей каждую из блочных матриц до циклической матрицы для снижения, таким образом, емкости запоминающего устройства и упрощения операций исключающего ИЛИ. Проверочная матрица, которая ограничена подобным образом, конкретно упоминается как псевдо-циклический код. Эти процессы также имеют проблему в том, что сниженная шкала устройства и упрощенная обработка являются несовместимыми. Другими словами, процессы, использующие псевдо-циклические коды, требуют сложного управления, хотя размер устройства уменьшен, или применимы к дополнительно ограниченным кодам среди псевдо-циклических кодов, т.е. только кодов, к которым добавляются дополнительные ограничивающие условия.
Для достижения прогресса в применении кодирования с исправлением ошибок к различным системах связи и запоминающим устройствам, например магнитным запоминающим устройствам, желательно разработать схему кодирования для улучшения эффективности кодирования, достигаемой повторным декодированием согласно алгоритму сумма-произведение, в дополнение к устройству с малым размером для осуществления простого процесса кодирования.
Патентный документ 1: JP-2003-115768A
Патентный документ 2: JP-2004-72130A
Непатентная литература 1: Д.Дж.К. Макей, "Good Error-Correcting Codes Based on very sparse matrices" ("Хорошие коды с исправлением ошибок на основе очень разреженных матриц"), протоколы IEEE по теории информации, стр.399-431, март 1999 г.
Непатентная литература 2: Томас Ричардсон, Р.Урбанке "Efficient Encoding of Low-Density Parity-Check Codes" ("эффективное кодирования кодов с проверкой на четность с низкой плотностью"), протоколы IEEE по теории информации, стр.619-656, сентябрь 2001 г.
РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
Проблемы, которые должны быть решены изобретением
Так как кодирование в отношении кода с проверкой на четность с низкой плотностью осуществляется с использованием запоминающего устройства, например запоминающего устройства информационной матрицы и процессора, например, устройство, вычисляющее избыточную битовую последовательность, для осуществления операции обработки согласно уравнению (2), описанному выше, устройство кодирования очень большого размера, сравнимого со случаем циклического кодирования с помощью кода Рида-Соломона или сверточного кодирования. Из-за этой проблемы, если кодирование с исправлением ошибок согласно вышеизложенному уровню техники применяется к системам, например спутниковым системам связи, наземным микроволновым системам связи и системам мобильной связи, то сложно сделать процесс простого кодирования и уменьшение размера устройства и повышенную эффективность кодирования совместимыми друг с другом.
Целью настоящего изобретения является предоставление способа кодирования исправления ошибок на основе кодирования с проверкой четности с низкой плотностью, который позволяет уменьшить устройство кодирования с исправлением ошибок в размере и упростить конфигурацию и который может достичь большего выигрыша кодирования на основе повторного декодированию.
Другой целью настоящего изобретения является предоставление устройства кодирования исправления ошибок на основе кодирования с проверкой четности с низкой плотностью, которое является малым в размере и простым в конфигурации и которое может достичь большого выигрыша кодирования на основе повторного декодирования.
Средство для решения проблем
Способ кодирования исправления ошибок согласно настоящему изобретению, который использует код с проверкой на четность с низкой плотностью, включает в себя: разделение информационной битовой последовательности, которая имеет длину К, которую необходимо обработать для кодирования исправления ошибок, на (m-r) частей первых блоков, каждый из которых содержит битовую последовательность, которая имеет длину n, и r частей вторых блоков, которые содержат соответствующие битовые последовательности, которые имеют длины k1, k2, …, kr, где К, m, n являются положительными целыми числами, r целое число в интервале 1≤r≤m, и k1, k2, …, kr целые числа в интервале 0≤k1, k2, …, kr≤n-1; первую арифметическую операцию для осуществления полиномиального умножения на (m-r) частей первых блоков, вывод r частей битовых последовательностей, которые имеют длину n; вторую арифметическую операцию для осуществления полиномиального деления и полиномиального умножения на r частей вторых блоков и r частей результатов операций первой арифметической операции, вывод битовой последовательности, включая избыточные битовые последовательности, которые имеют соответствующие длины n-k1, n-k2, …, n-kr.
Устройство кодирования исправления ошибок согласно настоящему изобретению, которое использует код с проверкой на четность с низкой плотностью, включает в себя: разделитель для разделения информационной битовой последовательности, которая имеет длину К, которую необходимо обработать для кодирования исправления ошибок, на (m-r) частей первых блоков, каждый из которых содержит битовую последовательность, которая имеет длину n, и r частей вторых блоков, которые содержат соответствующие битовые последовательности, которые имеют длины k1, k2, …, kr, где К, m, n являются положительными целыми числами, r - целое число в интервале 1≤r≤m, и k1, k2, …, kr целые числа в интервале 0≤k1, k2, …, kr≤N-1; r частей первых арифметических процессоров для осуществления полиномиального умножения на (m-r) частей первых блоков, и каждый выводит битовые последовательности, которые имеют длину n, как результат операции; второй арифметический процессор для осуществления полиномиального деления и полиномиального умножения на r частей вторых блоков и результатов операций, соответственно обеспечиваемых параллельно от r частей первых арифметических процессоров, и вывод битовой последовательности, включая избыточные битовые последовательности, которые имеют соответствующие длины n-k1, n-k2, …, n-kr.
В устройстве кодирования с исправлением ошибок согласно настоящему изобретению каждый из первых арифметических процессоров может включать в себя, например, максимум из (m-r) частей полиномиальных схем умножения. Например, второй арифметический процессор может включать в себя первый полиномиальный производящий деление и умножение процессор для параллельного осуществления не более чем одного полиномиального деления и не более чем (r-1) полиномиальных умножений на второй блок, который имеет длину kr, результаты операций от r частей первых арифметических процессоров, вывод (n-kr) битов и (r-1) частей битовых последовательностей, которые имеют длину n избыточных битовых последовательностей; р-ый процессор, производящий деление и умножение, где p является целым числом в интервале 2≤p≤r для параллельного осуществления не более чем одного полиномиального деления и не более чем (r-p) полиномиальных умножений на (r-р+1) частей битовых последовательностей, которые имеют длину n, предоставляемую от (p-1)-го процессора, производящего деление и умножение, и второй блок, который имеет длину kr-p+1, и вывод (n-kr-p+1) битов и (r-p) части битовых последовательностей, которые имеют длину n избыточных битовых последовательностей. В этом случае, например, r-ый процессор, производящий полиномиальное деление и умножение, может включать в себя не более чем одну схему полиномиального деления и не более чем (r-q) частей схем полиномиального умножения, где q является целым числом в интервале 1≤q≤r.
Подобный процессор полиномиального деления и умножения может использовать логические состояния соединения, например, для создания полинома, чтобы служить в качестве делителя в схеме полиномиального деления, и полинома для определения множителей в схемах полиномиального умножения. В этом случае могут использоваться серии полиномов, ассоциированных с минимальными полиномами по простому полю элементов конечного поля как максимум из r частей полиномов, соответствующих соединениям в схеме полиномиального деления, и полиномы, соответствующие соединениям в схеме полиномиального деления, могут быть выбраны из условия, что матрица, полученная произведением полинома на произведение полинома, соответствующего устройству, производящему полиномиальное деление, является разреженной матрицей. С помощью полиномов, которые используются и выбираются таким образом, эффективность кодирования может быть увеличена для операции эффективной обработки.
Согласно настоящему изобретению предусматривается способ и устройство кодирования на основе кода с проверкой на четность с низкой плотностью, который характеризуется малым размером устройства и простой установкой устройства и которое допускает достижение высокой эффективности кодирования согласно схеме повторного декодирования.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Фиг.1 является блок-схемой, которая показывает пример расположения устройства кодирования с исправлением ошибок согласно существующему уровню техники;
Фиг.2 - это блок-схема, показывающая расположение устройства кодирования с исправлением ошибок согласно примерному варианту осуществления настоящего изобретения;
Фиг.3 является блок-схемой, которая показывает пример конфигурации процессора полиномиального умножения;
Фиг.4 является блок-схемой, которая показывает пример конфигурации схемы полиномиального умножения;
Фиг.5 является блок-схемой, которая показывает пример конфигурации процессора полиномиального деления и умножения;
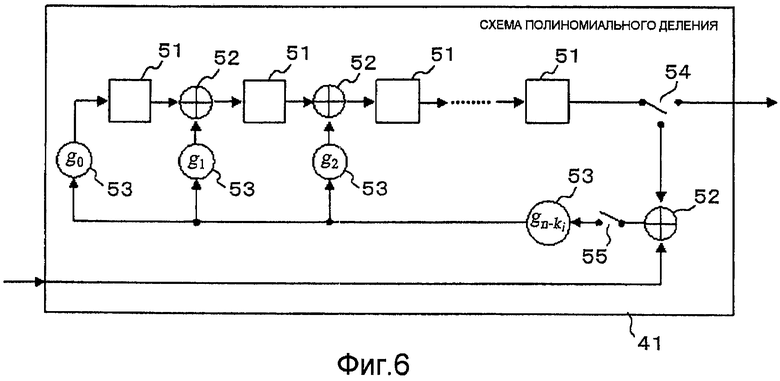
Фиг.6 является блок-схемой, которая показывает пример конфигурации схемы полиномиального деления;
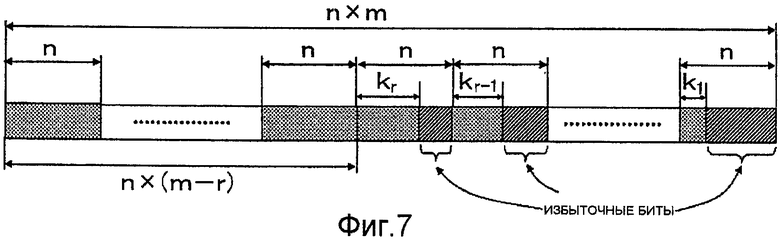
Фиг.7 является схемой, которая показывает пример формата кадра для кодовой последовательности битов;
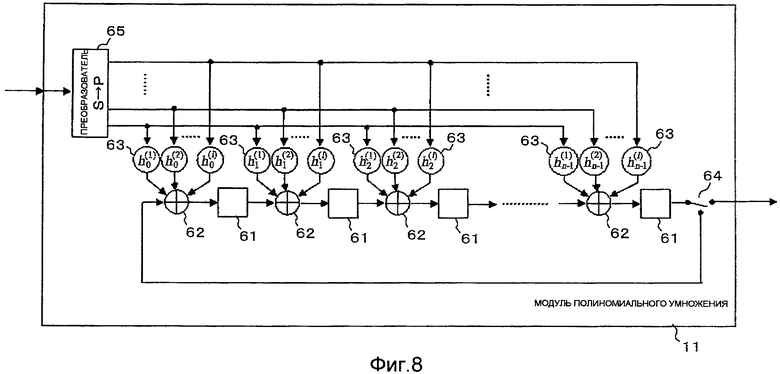
Фиг.8 является блок-схемой, которая показывает другой пример конфигурации процессора полиномиального умножения;
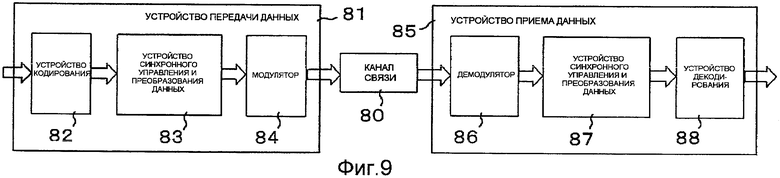
Фиг.9 является блок-схемой, которая показывает пример конфигурации системы обмена данными, которая использует устройство кодирования согласно настоящему изобретению.
Описание символов ссылок:
11 Процессор полиномиального умножения
12 Процессор полиномиального деления и умножения
13, 14, 23, 34, 54, 55, 65, 73 Переключатели
21, 42 Схемы полиномиального умножения
22, 32, 43, 52, 62 Схемы исключающего ИЛИ
31, 51, 61 Триггеры
33, 53, 63 Соединительные элементы
41 Схема полиномиального деления
44 Селектор
45, 46 Входные выводы
47, 48 Выходные выводы
65 Последовательно-параллельный преобразователь
71 Устройство, вычисляющее избыточную битовую последовательность
72 Запоминающее устройство матричной информации
81 Устройство передачи данных
82 Устройство кодирования
83, 87 Устройства синхронного управления и преобразования данных
84 Модулятор
85 Устройство приема данных
86 Демодулятор
88 Устройство декодирования
Наилучший режим осуществления изобретения:
Устройство кодирования с исправлением ошибок согласно примерному варианту осуществления настоящего изобретения, показанное на фиг.2, осуществляет кодирование с исправлением ошибок на основе кода с проверкой на четность с низкой плотностью информационной битовой последовательности, предоставляемой как вход для формирования, таким образом, кодовой битовой последовательности. Устройство кодирования с исправлением ошибок включает в себя: r частей процессоров 11 полиномиального умножения, расположенных параллельно, где r представляет собой целое число 1 или больше; r частей процессоров 12 полиномиального деления и умножения, расположенных в сериях; переключатель 13 на стороне ввода и переключатель 14 на стороне вывода. Для того чтобы отличить друг от друга r частей расположенных процессоров 12 полиномиального деления и умножения, они обозначаются от [1] до [r], как описано ниже. Переключатель 13 служит для назначения информационной битовой последовательности, предоставляемой устройству кодирования с исправлением ошибок, какому-либо одному из процессоров 11 полиномиального умножения. Переключатель 14 служит для последовательного выбора информационной битовой последовательности и r частей выводов от процессора [1] полиномиального деления и умножения на конечном этапе для того, чтобы выводить кодовую битовую последовательность, в которой комбинируются информационная битовая последовательность и избыточная битовая последовательность, как описано ниже.
Схема кодирования в настоящем примерном варианте осуществления предоставляется с вводом, представленным информационной битовой последовательностью, которая имеет длину, представленную К битами, и выводит кодовую битовую последовательность, которая имеет длину, представленную n·m битами. В данном документе длина К битов информационной битовой последовательности выражена с помощью следующего выражения:
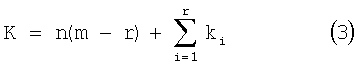
К битов в кодовой битовой последовательности, которая имеет длину n·m битов, находятся в полном соответствии с вводимой информационной битовой последовательностью, которая имеет длину К битов. Следовательно, схема кодирования в настоящем примерном варианте осуществления является схемой систематического кодирования. Подробности конфигурации устройства кодирования с исправлением ошибок согласно примерному варианту осуществления рассмотрены ниже. Если не указано иное, в дальнейшем описании длина представляет собой длину битов.
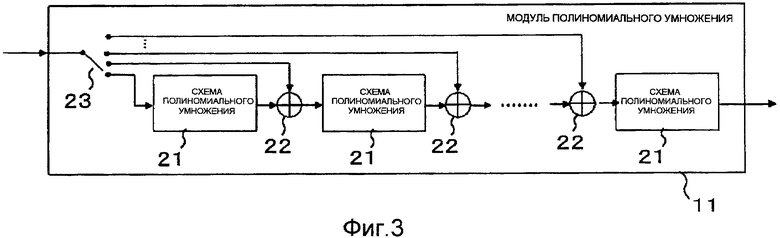
Процессоры 11 полиномиального умножения, r частей которых расположены, являются идентичными в расположении друг к другу, и каждый включает в себя, как показано на фиг.3, не более чем (m-r) частей схем 21 полиномиального умножения, схемы 22 исключающего ИЛИ, которых на одну меньше, чем схем 21 полиномиального умножения, и переключатель 23. Схемы 21 полиномиального умножения, (m-r) частей которого расположены, соединены последовательно друг с другом с помощью схем 22 исключающих ИЛИ. Переключатель 23 является переключателем с одним входом и с (m-r) выходами и предоставляет входную информационную битовую последовательность первой схеме 21 полиномиального умножения, т.е. схеме 21 полиномиального умножения на левой стороне фиг.3 либо одной из (m-r-1) частей схем 22 исключающего ИЛИ. Вывод из конечной схемы 21 полиномиального умножения, т.е. схемы 21 полиномиального умножения на правой стороне фиг.3, предоставляется как вывод процессора 11 полиномиального умножения в процессор 12 полиномиального деления и умножения на следующем этапе.
Процессор 11 полиномиального умножения принимает n(m-r) бит как вход из информационных битов, которые имеют длину К, как указано уравнением (2), и выводит битовую последовательность, которая имеет длину n. Выходная битовая последовательность предоставляется процессору 12 полиномиального деления и умножения на последующем этапе. Битовая последовательность, которая имеет длину n(m-r), разделяется на сегменты, каждый из которых содержит n битов, которые распределены на (m-r) частей схем 21 полиномиального умножения с помощью переключателя 23. Например, с первого по n-й биты последовательно предоставляются первой схеме 21 полиномиального умножения, т.е. схеме 21 полиномиального умножения на левом крае, как показано, и с (n+1)-го по 2n-й бит последовательно предоставляются через схему 22 исключающего ИЛИ второй схеме 21 полиномиального умножения, т.е. второй схеме 21 полиномиального умножения от левого края, как показано. Аналогично, с (jn+1)-го no (j+1)n-й биты, где j является целым числом в интервале 2≤j≤m-r-1, последовательно предоставляются через j-ю схему 22 исключающего ИЛИ (j+1)-й схеме 21 полиномиального умножения.
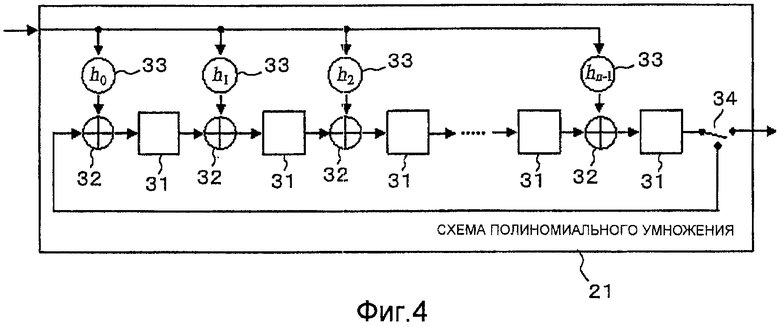
Схемы 21 полиномиального умножения в каждом из процессоров 11 полиномиального умножения являются идентичными в расположении друг к другу. Как показано на фиг.4, схема 21 полиномиального умножения содержит n частей триггеров 31, используемых как регистры, где n является положительным целым числом, не более чем n частей схем 32 исключающего ИЛИ, соединительные элементы 33, ассоциированные соответственно со схемами 32 исключающего ИЛИ, чтобы предоставлять им битовую последовательность, предоставляемую схемой 21 полиномиального умножения, и переключатель 34. Соединительные элементы 33, которые находятся в состоянии соединения или разъединения, определяемом в зависимости от проверочной матрицы. Схемы 32 исключающего ИЛИ упорядочены на соответствующих входных сторонах триггеров 31. С помощью схем 32 исключающего ИЛИ n частей триггеров 31, которые ассоциированы с соответствующими схемами 32 исключающего ИЛИ, последовательно соединены друг с другом. Переключатель 34 соединен со входом триггера 31 на конечном этапе. Переключатель 34 служит для выборочного предоставления вывода от триггера 31 на конечном этапе как вывод схемы 21 полиномиального умножения вовне или для возвращения вывода от триггера 31 на конечном этапе в триггер 31, т.е. триггер 31 на левом крае фиг.4, с помощью схемы 32 исключающего ИЛИ на первом этапе.
Схема 21 полиномиального умножения является, таким образом, конфигурацией из n-битовых вводов и n-битовых выводов. Когда вывод от триггера 31 на конечном этапе предоставляется триггеру 31 на первом этапе с помощью переключателя 34, схеме 21 полиномиального умножения последовательно предоставляется входная битовая последовательность из n битов. Когда схеме 21 полиномиального умножения предоставляются все биты, она управляет переключателем 34 для последовательного вывода данных из n частей триггеров 31 (т.е. регистров). Как показано на фиг.4, n частей соединительных элементов 33 согласуются, соответственно, с заданной битовой последовательностью h0, h1, hn-1 из n битов и устанавливаются в соединенном состоянии или разъединенном состоянии в зависимости от того, равен ли соответствующий бит 1 или 0. Соединенное состояние является состоянием, в котором входная битовая последовательность для схемы 21 полиномиального умножения предоставляется с помощью соединительных элементов 33 для схем 32 исключающего ИЛИ. Разъединенное состояние является состоянием, в котором входящая битовая последовательность для схемы 21 полиномиального умножения не предоставляется для схем 32 исключающего ИЛИ. Если j является целым числом в интервале 0≤j≤n-1, тогда hj равно 1, соединительный элемент, отмеченный hj, находится в соединенном состоянии, и когда hj равен 0, соединительный элемент, отмеченный hj, находится в разъединенном состоянии. Таким образом, схема 21 полиномиального умножения осуществляет полиномиальное умножение с помощью полинома, который имеет коэффициенты, представленные битовой последовательностью h0, h1, …, hn-1 из n битов. Пример способа выбора битовой последовательности h0, h1, …, hn-1 описан ниже.
Для того чтобы отличить друг от друга r частей процессоров 12 полиномиального деления и умножения, которые соединены последовательно, эти процессоры полиномиального деления и умножения обозначены от [1] до [r]. Как показано на фиг.2, процессор полиномиального деления и умножения на стороне входа, т.е. стороне процессора 11 полиномиального умножения, обозначен как процессор [r] полиномиального деления и умножения, и процессор полиномиального деления и умножения, расположенный на выводе процессора [r] полиномиального деления и умножения, обозначен как процессор [r-1] полиномиального деления и умножения. Аналогично, процессор полиномиального деления и умножения с правого края фиг.2 обозначен как процессор [1] полиномиального деления и умножения.
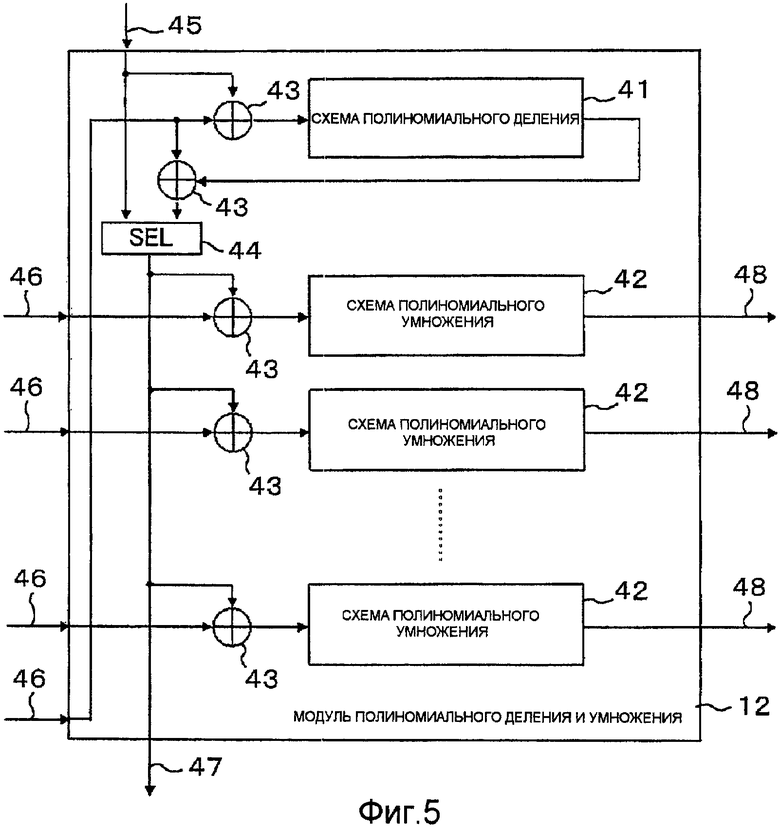
Если i является целым числом в интервале 1≤i≤r, тогда процессор [i] полиномиального деления и умножения среди процессоров 12 полиномиального деления и умножения содержит, как показано на фиг.5, не более чем одну схему 41 полиномиального деления и не более чем (i-1) частей схем 42 полиномиального умножения. Схемы 42 полиномиального умножения могут быть теми же самыми, что и схема полиномиального умножения, показанная на фиг.4. Схема 41 полиномиального деления описана ниже.
Последовательно расположенные r частей процессоров 12 полиномиального деления и умножения включают в себя различное число схем полиномиального умножения в зависимости от их положений в последовательно соединенной матрице. Соответственно, каждый из процессоров полиномиального деления и умножения задан числом их схем полиномиального умножения. В устройстве кодирования, показанного на фиг.2, процессор [r] полиномиального деления и умножения включает в себя (r-1) или меньше частей схем 42 полиномиального умножения, и процессор [r-1] полиномиального деления и умножения включает в себя (r-2) или меньше частей схем 42 полиномиального умножения. Как описано выше, процессор [i] полиномиального деления и умножения включает в себя (i-1) или меньше частей схем 42 полиномиального умножения. Если умножение нулевого полинома принимается во внимание, тогда, так как нет необходимости предоставлять схему умножения для умножения нулевого полинома, процессор [i] полиномиального деления и умножения включает в себя (i-1) схем 42 полиномиального умножения. Процессор [i] полиномиального деления и умножения описывается ниже.
Процессор [i] полиномиального деления и умножения содержит, в дополнение к не более чем одной схеме 41 полиномиального деления и не более чем (i-1) частям схем 42 полиномиального умножения, две схемы 43 исключающего ИЛИ, ассоциированные со схемой 41 полиномиального деления, и схемы 43 исключающего ИЛИ, ассоциированные с соответствующими схемами 42 полиномиального умножения, селектор (SEL) 44, вывод 45 для предоставления информационной битовой последовательности от переключателя 13 (см. фиг.2), i частей выводов 46 для предоставления битовых последовательностей параллельно от процессора [i+1] полиномиального деления и умножения на предыдущем этапе, вывод 47 для предоставления битовой последовательности переключателю 14 (см. фиг.2) и (i-1) частей выводов 48 для вывода битовых последовательностей параллельно процессору [i-1] полиномиального деления и умножения на последующем этапе. Из i частей выводов 46 первые (i-1) частей выводов соединены с помощью схем 43 исключающего ИЛИ с соответствующими схемами 42 полиномиального умножения. Выходные выводы схем 42 полиномиального умножения соединены с соответствующими выводами 48. Эти схемы 43 исключающего ИЛИ предоставляются общим выводом от селектора 44.
Вывод селектора 44 также соединен с выводом 47. Из выводов 46 оставшийся один вывод 46 соединен с оставшимися двумя схемами 43 исключающего ИЛИ. Одной из этих схем 43 исключающего ИЛИ предоставляется битовая последовательность с вывода 45 и соединяется со входом схемы 41 полиномиального деления. Другой схеме 43 исключающего ИЛИ предоставляется выходящая битовая последовательность от схемы 41 полиномиального деления и соединяется с одним из входных выводов селектора 44. Другой входной вывод селектора 44 соединяется с выводом 45.
Когда i=r, в процессоре [r] полиномиального деления и умножения r частей выводов 46 соединены с соответствующими выходными выводами из r частей процессоров 11 полиномиального умножения. Когда i=1, в процессоре [1] полиномиального деления и умножения можно обойтись без схем 42 полиномиального умножения и выводов 48.
Процессору [i] полиномиального деления и умножения, как описано выше, предоставляется ki бит из информационных битов, которые имеют длину К, указанную уравнением (2), через вывод 45, и также параллельные наборы из i битов из n·i битов от процессора [i+1] полиномиального деления и умножения на предыдущем этапе через выводы 46. Когда i=r, выводы 46 получают соответствующие биты выходов из r частей процессоров полиномиального умножения. Процессор [i] полиномиального деления и умножения выводит битовую последовательность, которая имеет длину n, как часть кодированной битовой последовательности с вывода 47 и также выводит параллельно всего n(i-1) битов битовой последовательности, которая имеет длину n, из (i-1) частей схем полиномиального умножения через выводы 48. Схема 41 полиномиального деления принимает вход, формируемый операцией исключающего ИЛИ над ki битами, последовательно предоставляемыми с вывода 45, и первыми ki битами из n битов, последовательно предоставляемых с вывода 46, и последовательно выводит (n-ki) битов после того, как схема 41 полиномиального деления приняла вход. Выход из (n-ki) битов со схемы 41 полиномиального деления и последних (n-ki) битов из n битов, последовательно предоставляемых с вывода 46, подвергается операции исключающего ИЛИ для получения выхода, который выдается через селектор 44 на входы схем 42 полиномиального умножения. Селектор 44 принимает первый вход, представленный ki битами, последовательно предоставляемыми с вывода 45, и второй вход, формируемый операцией исключающего ИЛИ над выходом схемы полиномиального деления и последними (n-ki) битами из n битов, последовательно предоставляемых с вывода 46, выборочно переключает первый и второй входы и последовательно выводит всего n битов. n битов, которые доставляются от селектора 44, выдаются как n битов из n·m битов кодированной битовой последовательности через вывод 47. Схемы 42 полиномиального умножения принимают входы, формируемые операцией исключающего ИЛИ над выходом селектора 44 и n битами, последовательно предоставляемыми на выводы 46, и последовательно выдают результат умножения из n битов через выводы 48.
Предполагается, что i является целым числом в интервале 1≤i≤r, как описано выше, и схема 41 полиномиального деления в процессоре [i] полиномиального деления и умножения описана ниже со ссылкой на фиг.6.
Схема 41 полиномиального деления содержит (n-ki) частей триггеров 51, где ki является целым числом в интервале 0≤ki≤n, не более чем (n-ki) частей схем 52 исключающего ИЛИ, (n-ki+1) частей соединительных элементов 53 и переключатели 54, 55. (n-ki+1) частей соединительных элементов 53 соответствуют битам битовой последовательности g0, g1, …, gn-ki, которая имеет заранее определенную длину (n-ki+1) битов, и установлены в соединенном состоянии или разъединенном состоянии в зависимости от значений соответствующих битов. А именно, если j является целым числом в интервале 0≤j≤n-ki, тогда (j+1)-й соединительный элемент 53, т.е. соединительный элемент, отмеченный "gj" на фиг., находится в соединенном состоянии, когда бит gj равен 1, и в разъединенном состоянии, когда бит gj равен 0. (n-ki) частей триггеров 51 соединены последовательно друг с другом с помощью схем 52 исключающего ИЛИ, каждая из которых вставлена между соседними схемами триггеров 51. Переключатель 54 служит для выборочного предоставления вывода от триггера 51 на конечном этапе как вывода схемы 41 полиномиального деления вовне или предоставления вывода от триггера 51 на конечном этапе в оставшуюся одну схему 52 исключающего ИЛИ, т.е. конечную схему 52 исключающего ИЛИ.
Конечная схема 52 исключающего ИЛИ получает битовую последовательность, которая предоставляется схеме 41 полиномиального деления, и вывод конечной схемы 52 исключающего ИЛИ подается через переключатель 55 на (n-ki+1)-й соединительный элемент, т.е. соединительный элемент, соответствующий биту gn-ki. Первый триггер 51, т.е. триггер 51 на правом крае на фиг.6, получает вывод от соединительного элемента 53, соответствующего биту gn-ki, с помощью соединительного элемента 53, соответствующего биту g0. В оставшихся триггерах 51 схемы 52 исключающего ИЛИ располагаются в их входных частях и получают вывод от соединительного элемента 53, соответствующего биту gn-ki с помощью соответствующего соединительного элемента 53, соответствующего битам g1, …, gn-ki-1.
Подобная схема 41 полиномиального деления принимает последовательный ввод ki битов, когда переключатель установлен на конечной стороне схемы 52 исключающего ИЛИ, сдвигает переключатель 54 после того, как он принял последовательный ввод, и последовательно выводит (n-ki) битов, которые сохранены в (n-ki) частях триггеров. Другими словами, схема 41 полиномиального деления осуществляет полиномиальное деление над входящей битовой последовательностью ki битов и полиномом, который имеет коэффициенты, представленные битами битовой последовательности g0, g1, …, gn-ki из (n-ki+1) бит. Пример способа выбора для битовой последовательности g0, g1, …, gn-ki описан позже.
Проверочная матрица, соответствующая устройству кодирования с исправлением ошибок на фиг.2, описана ниже. Проверочная матрица выражена уравнением (4):
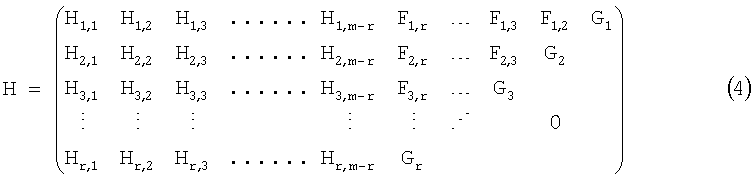
Проверочная матрица согласно уравнению (4) является блочной матрицей r×m и имеет компоненты, каждый из которых содержит циклическую матрицу n×n. Нижняя правая треугольная часть уравнения (4), т.е. часть, указанная с помощью "0" жирным в уравнении, содержит n×n циклических матриц, которые являются нулевыми матрицами. Как указано с помощью уравнения (5) ниже, циклическая матрица n×n имеет второй вектор-строку, равный первому вектору-строке, который сдвинут на один бит вправо, и k-й вектор-столбец, равный первому вектору-строке, который сдвинут на (k-1) бит вправо, где k является целым числом в интервале 2≤k≤n.

Первый вектор-строка циклической матрицы n×n уравнения (5) может быть выражен как полином (n-1)-го порядка или меньше, как показано в уравнении (6).
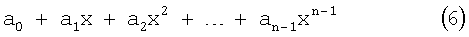
Предполагается, что i является целым числом в интервале 1≤i<r, j является целым числом в интервале 1≤j≤m-r, v является целым числом в интервале 2≤v≤r, и u является целым числом в интервале 1≤u≤t-1. Первый вектор-строка Hi,j в уравнении (4) выражен как полином (n-1)-го порядка или меньше, обозначенный с помощью h(i,j) (х), первый вектор-строка Fs,t в уравнении (4) - как полином (n-1)-го порядка или меньше, обозначенный с помощью f(u,v) (х), и первый вектор-строка Gi в уравнении (4) - как полином (n-1)-го порядка или меньше, обозначенный с помощью g(i) (х).
Как описано выше, схемы 21 полиномиального умножения в процессоре 11 полиномиального умножения и схемы 42 полиномиального умножения в процессоре 12 полиномиального деления и умножения созданы, как показано на фиг.4. В этих схемах полиномиального умножения битовая последовательность h0, h1, …, hn-1 из n битов для определения того, находятся ли соединительные элементы 33 в соединенном состоянии или разъединенном состоянии, определяется с помощью выбора полиномов h(i,j) (х), f(u,v) (x) описанных выше. Выбор битовой последовательности g0, g1, …, gn-ki из (n-ki+1) битов для определения соединений схемы 41 полиномиального деления в процессоре 12 полиномиального деления и умножения определяется с помощью выбора полинома g(i) (х). Пример выбора полиномов h(i,j) (x), f(u,v) (х), g(i) (х) описывается ниже.
Предполагается, что целое число q является степенью 2, т.е. q=2s где s является положительным целым числом, и целое число n равно n=q-1. Тогда g(i) (х) определяется согласно уравнению (7) в отношении простейшего элемента α конечного поля GF(q), которое имеет q частей элементов и целое число i, которое удовлетворяет 1≤i≤r.
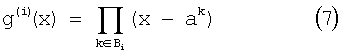
где Bi представляет собой подмножество целых чисел в интервале от 0 до q-2. Когда полином, соответствующий уравнению (7), выведен, коэффициенты Bi равны 0 либо 1. Следовательно, g(i) (х) является полиномом, порожденным умножением полиномов на простое поле (GF(2)) элементов GF(q), определяемых Вi. Подмножества B1, B2, …, Вr удовлетворяют следующему отношению (уравнение (8)):
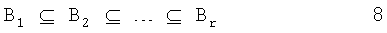
Это значит, что когда i и j являются целыми числами, принадлежащими интервалам 1≤i≤r, 1≤j≤r, g(i) (x) является делимым на g(i) (х), если i<j.
Полином h(i,j) (х) создан как множественный полином g(i) (х) с модулем хn-1. Другими словами, полином h(i,j) (x) (n-1)-го порядка или меньше создан как удовлетворяющий условию уравнения (9).
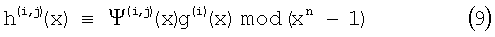
где i является целым числом в интервале 1≤i≤r, j является целым числом в интервале 1≤j≤m-r и ≡Ψ(i,j)(x) является полиномом (n-1)-го порядка или меньше, в котором коэффициенты ограничений равны 0 или 1. Как с полиномом h(i,j)(x) полином f(u,v)(х), описанный выше, создается как множественный полином g(i)(x) с модулем xn-1. Другими словами, полином f(u,v)(x) (n-1)-го порядка или меньше создан как удовлетворяющий условию уравнения (10).
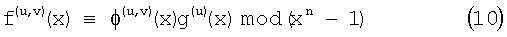
где v является целым числом в интервале 2≤v≤r u является целым числом в интервале 1≤u≤v-1, и ϕ(u,v)(x) является полиномом (n-1)-го порядка или меньше, в котором коэффициенты ограничений равны 0 или 1.
Соединения схем 21 полиномиального умножения в процессоре 11 полиномиального умножения описаны ниже. Со ссылкой на фиг.4, где показана схема полиномиального умножения, соединительные элементы 33 установлены в соединенное состояние или разъединенное состояние в зависимости от заранее определенной битовой последовательности h0, h1, …, hn-1 из n бит. В частности, если j является целым числом в интервале 0≤j≤n-1, тогда hj равно 1, соединительный элемент, отмеченный "hj", находится в соединенном состоянии, и когда hj равен 0, соединительный элемент, отмеченный "hj" находится в разъединенном состоянии. Битовая последовательность из n битов для определения таких соединений выбирается следующим образом:
Так как устройство кодирования согласно настоящему примерному варианту осуществления включает в себя r частей процессоров 11 полиномиального умножения, как показано на фиг.2, r частей процессоров 11 полиномиального умножения пронумерованы 1, 2, …, r сверху на чертеже. Кроме того, так как каждый процессор 11 полиномиального умножения включает в себя не более чем (m-r) частей схем 21 полиномиального умножения, как показано на фиг.3, эти схемы полиномиального умножения пронумерованы 1, 2, …, m-r слева. Если предполагается, что i является целым числом в интервале 1≤i≤r, j является целым числом в интервале 1≤j≤m-r, и k является целым числом в интервале 0≤k≤n-1, тогда битовая последовательность из n бит, указывающая на соединения j-й схемы полиномиального умножения в i-м процессоре полиномиального умножения выражается с помощью h0 (i,j), h1 (i,j), …, hn-1 (i,j), где hk (i,j) используется как коэффициент ограничения хk в Ψ(i,j)(х) в уравнении (9). С помощью этого параметра возможно установить коэффициенты всех схем полиномиального умножения в процессорах 11 полиномиального умножения устройства кодирования, показанного на фиг.2, используя полином Ψ(i,j)(х) согласно уравнению (9).
Состояния соединительных элементов в схеме 41 полиномиального деления и схемы 42 полиномиального умножения процессоров 12 полиномиального деления и умножения описаны ниже.
Фиг.6 показывает расположения схемы 41 полиномиального деления. На фиг.6, как описано выше, находятся соединительные элементы 53 в соединенном состоянии или разъединенном состоянии, определяется с помощью заранее определенной битовой последовательности g0, g1, …, gn-ki (n-ki+1) битов. Если предполагается, что i является целым числом в интервале 1≤i≤n, и j является целым числом в интервале 1≤j≤n-ki, тогда, когда gj равен 1, соединительный элемент в части, отмеченной "gj", находится в соединенном состоянии, и когда gj равен 0, соединительный элемент в части, отмеченной "gj", наводится в разъединенном состоянии. Когда битовая последовательность (n-ki+1) битов, указывающая на состояния соединительных элементов в схеме полиномиального деления в процессоре [i] полиномиального деления и умножения выражена с помощью g0 (i), g1 (i), …, gn-k1 (i), gj (i) используется как коэффициент ограничения хj в полиноме σ(i)(х), который определяется из полинома g(i)(х) уравнения (8) на основе уравнения (11):
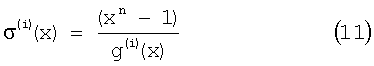
С помощью этого параметра возможно установить коэффициенты схемы 41 полиномиального деления, оказывающиеся в процессорах 12 полиномиального умножения устройства кодирования, показанного на фиг.2, используя полином g(i)(х) согласно уравнению (8).
Как показано на фиг.6, выход схемы 41 полиномиального деления соответствует разности, которая получена, когда полином, коэффициенты которого представлены входящей битовой последовательностью для схемы 41 полиномиального деления, поделен на полином σ(i)(х) согласно уравнению (11). Следовательно, если q(i)(x)=1, т.е. если σ(i)(х)=хn-1, тогда схема 41 полиномиального деления выводит входящую битовую последовательность как она есть.
Если предполагается, что v является целым числом в интервале 1≤v≤r и, u является целым числом в интервале 1≤u≤v-1, тогда каждый из соединительных элементов в u-й схеме 42 полиномиального умножения, рассмотренной выше (см. фиг.5), в v-м процессоре 12 полиномиального деления и умножения установлен либо в соединенное состояние, либо в разъединенное состояние в зависимости от коэффициента каждого из ограничений ϕ(u,v)(х) уравнения (10) тем же самым образом, как и схемы 21 полиномиального умножения в процессорах 11 полиномиального умножения.
Порядок полинома σ(i)(х) согласно уравнению (11) для определения состояния соединительного элемента 53 в схеме 41 полиномиального деления соответствует (n-ki), и ранг R матрицы Н согласно уравнению (4) задан следующим уравнением (12) согласно уравнениям с (7) по (11):
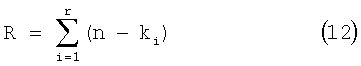
Следовательно, число избыточных битов в схеме кодирования, где матрица Н согласно уравнению (4) служит как проверочная матрица, указано с помощью R, показанного в уравнении (12), и число информационных битов находится в соответствии с К, показанным в уравнении (3). Длина битов одного блока равна сумме числа информационных битов, и число избыточных битов равно n·m.
Фиг.7 показывает пример формата кадра для кодированной битовой последовательности, которая имеет длину n·m битов, которая кодируется устройством кодирования с исправлением ошибок согласно настоящему примерному варианту осуществления. К битов в кодированной битовой последовательности согласно уравнению (3) находятся в полном соответствии с информационной битовой последовательностью, предоставляемой устройству кодирования.
Следовательно, схема кодирования согласно настоящему примерному варианту осуществления является схемой систематического кодирования.
Функционирование устройства кодирования с исправлением ошибок согласно настоящему примерному варианту осуществления рассмотрено ниже.
Устройству кодирования с исправлением ошибок, показанное на фиг.1, последовательно предоставляется информационная битовая последовательность, которая имеет длину К битов согласно уравнению (3), которая поделена на блоки для кодирования с исправлением ошибок. Переключатель 13 установлен для последовательного предоставления n(m-r) битов, в интервале от первого бита до n(m-r)-го бита, наряду с информационными битами, которые имеют длину К, для всех r частей процессоров 11 полиномиального умножения, которые расположены параллельно друг другу. В этот момент переключатель 14 установлен в положение для вывода входящих n(m-r) битов непосредственно как выход устройства кодирования. Когда n(m-r)-й бит введен в устройство кодирования, переключатель 12 устанавливается для ввода последовательных kr битов в процессор [r] полиномиального деления и умножения на первом этапе.
Процессору [r] полиномиального деления и умножения предоставляются информационные биты из kr битов, описанных выше, и всего n·r битов выводов от r частей процессоров 11 полиномиального умножения и выводов n(r-1) битов для предоставления в процессор [r-1] полиномиального деления и умножения на следующем этапе и n битов как вывод устройства кодирования. Переключатель 14 затем соединяется с выходным выводом процессора [r] полиномиального деления и умножения и выводит n битов. Если предполагается, что i является целым числом в интервале 2≤i≤r-1, тогда переключатель 13 аналогично сдвигается для предоставления информационной битовой последовательности из ki бит для процессора [i] полиномиального деления и умножения. Процессор [i] полиномиального деления и умножения обрабатывает ki битов из информационных битов и n·i битов, предоставляемых от процессора [i+1] полиномиального деления и умножения, и формирует n битов как вывод устройства кодирования и n(i-1) битов для предоставления процессору [i-1] полиномиального деления и умножения на следующем этапе. Если информационная битовая последовательность из К битов постоянно предоставляется устройству кодирования с исправлением ошибок согласно настоящему примерному варианту осуществления, тогда, так как каждый процессор 12 полиномиального деления и умножения требует n единиц времени для своей операции обработки, необходимо осуществлять задержку ввода информационной битовой последовательности (ki-1 бит) для процессора [i-1] полиномиального деления и умножения, который должны действовать следующим, в течение промежутка времени после того, как ki бит информационной битовой последовательности введены, пока не закончена операция обработки процессора [i] полиномиального деления и умножения и завершает свой вывод.
В конечном итоге, переключатель 13 сдвигается для ввода информационной битовой последовательности из k1 битов и для вывода n битов от процессора [2] полиномиального деления и умножения в процессор [1] полиномиального деления и умножения. Как следствие, процессор [1] полиномиального деления и умножения выводит n битов. Этот вывод n битов распределяется от устройства кодирования с помощью переключателя 14. В отношении соединений схем полиномиального деления, которые проиллюстрированы с помощью примера выше, когда g(i)(х)=1, тогда ki=0, и полиномиальное деление в процессоре [i] полиномиального деления и умножения опускается, как описано выше.
Подробности действия процессоров 11 полиномиального умножения описываются ниже. Как описано выше, каждому из процессоров 11 полиномиального умножения последовательно предоставляется n(m-r) бит, заключающихся в пределах от первого бита до n(m-r)-го бита информационной битовой последовательности. Эти n(m-r) бит разделены на наборы из n битов, которые распределяются, как показано на фиг.3, на (m-r) частей схем 21 полиномиального умножения в процессоре 11 полиномиального умножения. От первого бита до n-го бита последовательно предоставляются первой схеме полиномиального умножения, т.е. схеме полиномиального умножения на левом краю фиг.3. Когда n-й бит введен, переключатель 23 сдвигается для предоставления от (n+1)-го бита до 2n-го бита через схему 22 исключающего ИЛИ во вторую схему полиномиального умножения, т.е. вторую схему полиномиального умножения с левого края на фиг.3. Другими словами, каждые из от (n+1)-го бита по 2n-й бит и каждый из выходных битов от первой схемы полиномиального умножения подвергаются операции исключающего ИЛИ для получения вывода, который последовательно предоставляется на вторую схему полиномиального умножения. Аналогично, если предполагается, что j является целым числом в интервале 2≤j≤m-r-1, биты с (jn+1)-го по (j+1)n-й бит предоставляется с помощью схемы 22 исключающего ИЛИ на (j+1)-ю схему полиномиального умножения, и таким образом, каждый из битов с (jn+1)-го no (j+1)n-й бит и каждый из выходных битов из j-й схемы полиномиального умножения подвергаются операции исключающего ИЛИ для получения вывода, который последовательно подается на (j+1)-ю схему полиномиального умножения. Вывод из n битов от схемы полиномиального умножения на конечном этапе, т.е. от (m-r)-й схемы полиномиального умножения, является выводом от процессора 11 полиномиального умножения, показанного на фиг.3.
Действие схемы полиномиального умножения описано ниже со ссылкой на фиг.4. Данные в триггерах 31, используемые как регистры, инициализируются в ноль, и n битов битовой последовательности последовательно вводятся, по одному биту, на схему полиномиального умножения. В течение этого времени переключатель 34 установлен на сторону контура обратной связи, т.е. сторону, которая не является стороной выхода. Когда все n битов введены, переключатель 34 сдвигается на последовательный вывод данных, сохраненных в триггерах 31.
Действие процессоров 12 полиномиального деления и умножения описано ниже со ссылкой на фиг.5. Как описано выше, каждый из процессоров 12 полиномиального деления и умножения содержит не более чем одну схему 41 полиномиального деления и не более чем (r-1) частей схем 42 полиномиального умножения. Каждый из процессоров 12 полиномиального деления и умножения отличается числом схем 42 полиномиального умножения, включенных в них. Однако процессоры 12 полиномиального деления и умножения являются идентичными друг другу в основной операции. Когда операция обработки процессоров 11 полиномиального умножения, описанная выше, окончена, устройство кодирования согласно настоящему примерному варианту осуществления уже обеспечено n(m-r) битами из К битов информационной битовой последовательности согласно уравнению (3).
Процессору [r] полиномиального деления и умножения последовательно предоставляется с (n(m-r)+1)-го бита по (n(m-r)+kr)-й бит информационной битовой последовательности через вывод 45. В то же самое время процессору [r] полиномиального деления и умножения также последовательно предоставляется битовая последовательность из n битов от соответствующих r частей процессоров 11 полиномиального умножения через вывод 46. В то время как информационная битовая последовательность из kr битов предоставляется через вывод 45, информационная битовая последовательность с вывода 45 и битовая последовательность, вводимая с r-го вывода 46, т.е. вывода на нижнем конце, подвергаются операции исключающего ИЛИ для получения вывода, который предоставляется схеме 41 полиномиального деления. В этот момент селектор 44 устанавливается в положение для выбора ввода с вывода 45. Ввод с вывода 45 передается непосредственно от выходного вывода 47 вывода. Вывод от селектора 44 передается с выходного вывода 47 и также предоставляется (r-1) частям схем 43 исключающего ИЛИ. Входы от первого по (r-1)-й выводы 46, отличные от входа с вывода 46 в схему 41 полиномиального деления, предоставляются через схемы 43 исключающего ИЛИ, которые также получают вывод от селектора, для (r-1) частей схем 42 полиномиального умножения.
Когда ((n(m-r)+kr)-й бит введен через вывод 45, селектор 44 устанавливается так, что он выбирает вывод, формируемый операцией исключающего ИЛИ над выводом из схемы 41 полиномиального деления и данными, вводимыми с r-го вывода 46. В этот момент времени схема 41 полиномиального деления выводит (n-kr) битов. Выход с селектора 44 выдается через выходной вывод 47 как выход устройства кодирования, т.е. как последовательность избыточных битов, и также подвергается операции исключающего ИЛИ со входами от (r-1) частей выводов 46. Результаты операции исключающего ИЛИ предоставляются схемам 42 полиномиального умножения.
Из n битов, полученных с вывода 47, первые kr битов непосредственно представляют собой информационную битовую последовательность, вводимую с вывода 45, и последние (n-kr) битов служат избыточными битами. Обработка kr битов, находящихся в интервале от (n(m-r)+1)-го бита до (n(m-r)+kr)-го бита информационной битовой последовательности и первых kr битов битовой последовательности, вводимых с выводов 46, требуют kr единиц времени. Обработка вывода (n-kr) битов от схемы полиномиального деления и последних (n-kr) битов битовой последовательности, вводимой с вывода 46, требует (n-kr) единиц времени. Соответственно, процессор [r] полиномиального деления и умножения требует n единиц времени для своей операции обработки. Данные, хранимые в триггерах 31 (т.е. регистрах) в (r-1) частях схем 42 полиномиального умножения, передаются с вывода 48 и предоставляются процессору [r-1] полиномиального деления и умножения на следующем этапе.
Аналогично, если предполагается, что i является целым числом в интервале 2≤i≤r-1, тогда процессор [i] полиномиального деления и умножения формирует выход устройства кодирования из ki битов, вводимых с вывода 45, и n·i битов, вводимых от процессора [i+1] полиномиального деления и умножения на предыдущем этапе через вывод 46, и передает сформированный выход через вывод 47 и также формирует данные в качестве входа в процессор [i-1] полиномиального деления и умножения на следующем этапе. Сформированные данные передаются с выводов 48 процессора [i] полиномиального деления и умножения во время работы процессора [i-1] полиномиального деления и умножения на следующем этапе. Из n битов, передаваемых с вывода 47, первые ki битов непосредственно представляют собой информационную битовую последовательность с вывода 45, а последние (n-ki) битов служат избыточными битами.
В конечном счете, k0 битов, находящихся в интервале от (К-k0+1)-го бита до К-го бита из информационных битов вводятся в процессор [1] полиномиального деления и умножения. Процессор [1] полиномиального деления и умножения содержит не более чем один процессор 41 полиномиального деления, которому предоставляется ввод, формируемый операцией исключающего ИЛИ над первыми k0 битами из n битов, которые вводятся от процессора [2] полиномиального деления и умножения через выводы 46, и k0 битами, вводимыми через вывод 45. Из n битов, получаемых через вывод 47, первые k0 битов непосредственно представляют собой битовую последовательность, вводимую через вывод 45, и последние (n-k0) биты формируются операцией исключающего ИЛИ над выходом из (n-k0) битов из схемы 41 полиномиального деления и последних (n-k0) битов из n битов, вводимых через выводы 46.
Действие схемы полиномиального умножения описано ниже со ссылкой на фиг.6. Для краткости схема полиномиального деления в процессоре [r] полиномиального деления и умножения описана ниже. Однако схемы полиномиального деления в других процессорах полиномиального деления и умножения являются также идентичными в отношении основной операции.
В схеме 41 полиномиального деления данные в (n-kr) частях триггеров 51 (т.е. регистры) инициализируются в ноль, переключатель 54 устанавливается в положение контура обратной связи, т.е. положение, которое не является положением вывода, и переключатель закрыт. Когда kr битов из битовой последовательности последовательно предоставляются схеме 41 полиномиального деления, данные в регистре сдвига, составленном из триггеров 51, последовательно обновляются. Когда kr битов введены, переключатель 55 открывается, и переключатель 54 сдвигается в положение вывода, последовательно выводя данные из триггеров 51.
Как описано выше, когда устройству кодирования с исправлением ошибок согласно настоящему примерному варианту осуществления задана информационная битовая последовательность, которая имеет длину К битов, разделенная на блоки, где К является положительным целым числом, устройство кодирования с исправлением ошибок дополнительно делит информационную битовую последовательность на (m-r) частей блоков, каждый из которых имеет длину n, и r частей блоков имеют соответствующие длины k1, k2, k3, …, kr. Устройство кодирования с исправлением ошибок передает кодовую битовую последовательность, которая имеет длину m-n согласно формату кадра, показанного на фиг.7, используя проверочную матрицу согласно уравнению (4), которое соответствует коду с проверкой на четность с низкой плотностью. Здесь m, n представляют собой целые числа больше или равные 2, r целое число в интервале 1≤r≤m, и k1, k2, k3, …, kr соответствующие целые числа в интервале 0≤k1, k2, k3, …, kr≤n.
Максимум из r(m-r) частей схем 21 полиномиального умножения включены в общее количество r частей процессоров 11 полиномиального умножения. Максимуму r(m-r) частей схем 21 полиномиального умножения получают (m-r) частей блоков, каждый из которых имеет длину n, из битовых последовательностей, формируемых разделением входной информационной битовой последовательности, которая имеет длину К битов, как описано выше, и выдают соответствующие последовательности, каждая из которых имеет длину n. r частей процессоров 12 полиномиального деления и умножения включают в себя максимум r частей схем 41 полиномиального деления в целом и максимум r(r-1) частей схем 42 полиномиального умножения в целом. Используя эти схемы 41 полиномиального деления и схемы 42 полиномиального умножения, r частей процессоров 12 полиномиального деления и умножения получают блоки, которые имеют длины k1, k2, k3, …, kr, формируемые делением входной информационной битовой последовательности, которая имеет длину К битов, как описано выше, и выходные данные процессоров 11 полиномиального умножения, и выдают избыточные битовые последовательности, которые имеют соответствующие длины n-k1, n-k2, n-k3, …, n-kr.
Для определения того, находятся ли соединительные элементы 53 (см. фиг.6) в каждом из максимум r частей схем 41 полиномиального деления в соединенном состоянии или разъединенном состоянии, устройство кодирования согласно настоящему примерному варианту осуществления использует последовательности полиномов, ассоциированные с минимальными полиномами по простому полю элементов конечного поля как максимум из r частей полиномов. Устройство кодирования согласно настоящему примерному варианту осуществления также выбирает полиномы для определения состояния соединительных элементов в схемах 42 полиномиального умножения в процессорах 12 полиномиального деления и умножения из условия, так что матрица, сконфигурированная произведением полиномов на полином, соответствующий схеме 41 полиномиального деления, является разреженной матрицей. С помощью полиномов, которые используются и выбираются таким образом, эффективность кодирования может быть увеличена для эффективной операции обработки.
Более конкретный способ установки полиномов g(1)(x), g(2)(x), …, g(r)(x), который удовлетворяет уравнениям (7) и (8), описывается ниже как дополнительный пример настоящего изобретения.
Предполагается, что целое число q является степенью 2, т.е. q=2s, где s является положительным целым числом, и целое число n равно n=q-1. Тогда gL(x) определяется согласно уравнению (13) в отношении простейшего элемента α конечного поля GF(q), которое имеет q частей элементов и целое число L, которое удовлетворяет 0≤L≤s-1.
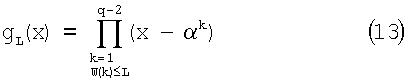
где W(k) представляет собой общую сумму, как целое число коэффициентов, когда целое число k в интервале 1≤k≤q-2 обрабатывается двоичным разложением. g0(x)=1. Когда выведен полином согласно уравнению (3), его коэффициенты равны 0 или 1. Используя полином gL(x) уравнения (13), g(i)(x) выбирается согласно уравнению (14).
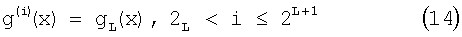
Предполагается, что g(1)(x)=g(2)(x)=1. Если предполагается, что i и j являются целыми числами в интервалах 1≤i≤r, 1≤j≤r, тогда, так как g(j)(x) является делимым на g(i)(x), если i<j, полином g(1)(x), g(2)(x), …, g(r)(x), созданный согласно уравнениям (13), (14) удовлетворяет требованиям уравнений (7), (8).
Если предполагается, что i является целым числом в интервале 1≤i≤r, и j является целым числом в интервале 1≤j≤m-r, полином h(i,j)(x) выбирается как множественный полином g(i) (х), как показано в уравнении (9). Если предполагается, что v является целым числом в интервале 2≤v≤r, и u является целым числом в интервале 1≤u≤v-1, полином f(u,v)(x) выбирается как множественный полином g(u)(x), как показано в уравнении (10), как с полиномом h(i,j)(x). Хотя полиномы h(i,j)(x), f(u,v)(x) могут быть гибко выбраны, они могут быть выбраны из условия, что проверочная матрица Н согласно уравнению (4), которое определяется полиномом g(i)(x) согласно уравнению (14) и полиномами h(i,j)(x), f(u,v)(x), находится в соответствии с матрицей, порождаемой преобразованием основных строк блочной матрицы Н', блоки которой представлены разреженными циклическими матрицами. Как результат, битовая последовательность, которая кодируется схемой кодирования согласно настоящему примерному варианту осуществления, является кодом проверки на четность с низкой плотностью и может декодироваться схемой повторного декодирования, например процессом декодирования суммы-произведения.
Конкретные числовые примеры описаны ниже. Целые числа s, q, упоминаемые выше, установлены s=3, q=8 и представляют собой простейший элемент конечного поля GF(8), которое имеет простейший полином x3+х+1. В этом случае n=7 и предполагается, что m=9 и r=3. Из уравнений (13), (14), g(1)(x)=g(2)(x)=1, g(3)(x) соответствует простейшему полиному, так что g(3)(x)=x3+х+1. Согласно уравнению (9) Ψ(i,j)(x) для определения h(i,j)(x), где i является целым числом в интервале 1≤i≤3, и j является целым числом в интервале 1≤j≤6, выбрано следующим образом:
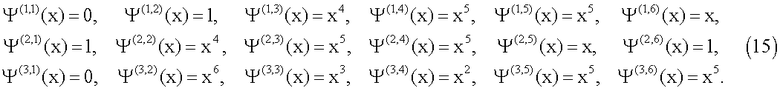
Согласно уравнению (10), ϕ(u,v)(x) для определения f(u,v)(x) выбирается как ϕ(1,3)(x)=1, ϕ(2,3)(x)=x5 и ф(1,2)(x)=х5. Все состояния соответствующих соединительных элементов в устройстве кодирования согласно настоящему примерному варианту осуществления определяются таким образом. Проверочная матрица Н согласно уравнению (4) также определяется, которая находится в соответствии с матрицей, порождаемой преобразованием основных строк матрицы Н' согласно следующему уравнению (16):
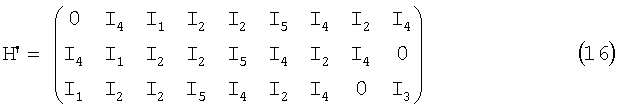
где "0" жирным шрифтом представляет собой матрицу 7×7, полностью состоящую из нулей. Если предполагается, что k является целым числом в интервале 0≤k≤6, Ik представляет собой матрицу циклических перестановок, где только аk равен 1, и все другие элементы равны 0. Используя процесс повторного декодирования, например, процесс декодирования суммы-произведения, который соответствует проверочной матрице Н', битовая последовательность, которая является кодированной с исправлением ошибок с помощью устройства кодирования согласно настоящему примерному варианту осуществления, может быть эффективно декодирована и достаточно точно.
В конечном итоге преимущества, получаемые установкой устройства кодирования согласно настоящему примерному варианту осуществления и устройство для осуществления процесса повторного декодирования, например, процесс декодирования суммы-произведения, который проектируется на основе устройства кодирования, соответственно со стороны передачи и стороны приема, описывается ниже с помощью числового примера. Целые числа s, q, упоминаемые выше, установлены как s=3, q=8 и представляют собой простейший элемент конечного поля GF(64), которое имеет простейший полином x3+x+1. В этом случае n=63 и предполагается, что m=65 и r=8. Из уравнений (13), (14), g(1)(x)=g(2)(x)=1, g(3)(x) и g(4)(x) соответствуют простейшему полиному, так что g(3)(x)=g(4)(x)=x6+x+1. Согласно уравнениям (13), (14), g(5)(x), g(6)(x), g(7)(x), g(8)(x) находятся в соответствии с полиномом g2(x), показанным в уравнении (17).
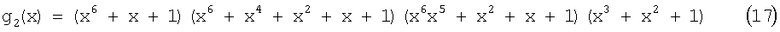
Что касается вышеизложенного конкретного примера, полином Ψ(i,j)(x), ϕ(u,v)(x) может быть выбран из условия, чтобы проверочная матрица согласно уравнению (4) находилась в соответствии с матрицей, порождаемой преобразованием основных строк блочной матрицы Н', компоненты которой включают в себя нулевые матрицы и матрицы циклических перестановок. В этот момент, так как n=63 и m=65, длина кода равна 4095 битов, и так как k1=k2=0, k3=k4=6, k5=k6=k7=k8=21, число информационных битов равно 3687 согласно уравнению (3). С помощью вышеуказанного выбора возможно создать устройство кодирования, которое имеет длину кода 4095 битов и длину информационных битов 3687 битов для декодирования битовой последовательности с высокой точностью, эффективно основываясь на процессе повторного декодирования, например процессе декодирования суммы-произведения.
Для осуществления связи с использованием сигнала, модулированного схемой модуляции BPSK (двоичная фазовая манипуляция) в среде аддитивного белого гауссовского шума, возможно достичь выигрыша кодирования, равного 3,5 дБ или выше, когда вероятность битовой ошибки равна 0,1% после декодирования, используя код, описанный выше, который имеет длину кода 4095 битов и 3687 информационных битов. При этом отношение увеличения полосы частот равно примерно 11%.
В настоящем конкретном примере, как описано выше, параметр r, соответствующий числу блоков строк матрицы согласно уравнению, (4) установлен на 8. Отношение кодирования и отношение увеличения полосы могут быть изменены без необходимости больших модификаций устройства кодирования, изменяя параметр r. Например, только параметр r может быть переустановлен с 8 на 4 без изменения других устанавливаемых параметров, например, выбора полиномов. При этом блочная матрица Н имеет 4 блока строк и 65 блоков столбцов, и каждый блок строк находится в соответствии с первым по четвертый блоки строк блочной матрицы Н во время r=8. Аналогично каждый блок строк разреженной блочной матрицы Н', формируемой преобразованием основных строк блочной матрицы Н, находится в соответствии с первым по четвертый блоки строк разреженной блочной матрицы, где r=8. Устройство кодирования для r=4 может быть реализовано отдельными частями схем полиномиального умножения и схем полиномиального деления в устройстве кодирования для r=8. Схема, предоставляемая отделением нижних четырех из восьми параллельных процессоров полиномиального умножения и дополнительно разделением схем полиномиального деления и схем полиномиального умножения, соединенных с нижними четырьмя процессорами полиномиального умножения в отношении процессоров [i] полиномиального деления и умножения, где i=8, 7, 6, 5 на фиг.2, находится в соответствии с конфигурацией устройства кодирования для r=4. В этом случае длина кода равна 4095 битов и длина информационных битов равна 3885 битов, с отношением увеличения полосы примерно 6,2%. В вышеуказанной среде передачи данных возможно достичь эффективности кодирования в 2,5 Дб или выше, когда вероятность ошибки в символе после декодирования равна 0,1%.
Устройство кодирования с исправлением ошибок согласно другому примерному варианту осуществления настоящего изобретения описано ниже.
В вышеуказанном варианте осуществления процессор 11 полиномиального умножения, показанный на фиг.3, содержит (m-r) частей схем 21 полиномиального умножения, соединенных последовательно друг с другом с помощью схем 22 исключающего ИЛИ, где m является положительным целым числом, и r является положительным целым числом в интервале 1<r<m. (m-r) частей схем полиномиального умножения, которые соединены последовательно друг с другом, могут быть расположены в параллельной конфигурации путем выполнения преобразования последовательного кода в параллельный над входными данными для процессора полиномиального умножения. Выводы от (m-r) частей схем полиномиального умножения, которые расположены в параллельной конфигурации, подвергаются операции исключающего ИЛИ для получения выхода процессора полиномиального умножения. Параллельная конфигурация является преимущественной в том, что число триггеров в процессорах полиномиального умножения снижено, так как триггеры совместно используются процессорами полиномиального умножения, расположенными в параллельной конфигурации.
Фиг.8 показывает подобный процессор полиномиального умножения, который включает в себя (m-r) частей схем полиномиального умножения, расположенных в параллельной конфигурации. Для краткости, предполагается, что (m-r) представлено посредством N. Процессор полиномиального умножения содержит: n частей триггеров 61, используемых как регистры, где n является положительным целым числом; не более чем n частей схем 62 исключающего ИЛИ с (N+1) входами; соединительные элементы 63, сгруппированные в наборы из N соединительных элементов, ассоциированных с соответствующими схемами 62 исключающего ИЛИ и имеющих соединенное состояние или разъединенное состояние, определяемое в зависимости от проверочной матрицы; переключатель 64 и преобразователь 65 последовательного кода в параллельный (S→Р) для преобразования последовательной входящей битовой последовательности в N (=m-r) параллельных битов. Схемы 62 исключающего ИЛИ выполнены для соответствующих триггеров 61 и соединены с входами триггеров, n частей триггеров 61, которые ассоциированы с соответствующими схемами 62 исключающего ИЛИ, соединены последовательно друг с другом с помощью схем 62 исключающего ИЛИ. Переключатель 34 соединен с выводом триггера 61 на конечном этапе. Переключатель 34 служит для выборочного предоставления вывода от триггера 61 на конечном этапе как вывода процессора полиномиального умножения вовне или для возвращения вывода от триггера 61 на конечном этапе в первый триггер 61, т.е. триггер 61 на левом краю фиг.8, с помощью схемы 62 исключающего ИЛИ на первом этапе.
Соединительные элементы 63, сгруппированные в наборы из N частей соединительных элементов, ассоциированных с соответствующими схемами 62 исключающего ИЛИ, служат для определения того, должны ли N частей выводов от преобразователя 65 последовательного кода в параллельный подаваться на соответствующую схему 62 исключающего ИЛИ или нет. Если предполагается, что i является целым числом в интервале 1≤i≤n, определяется, должны ли N частей выводов от преобразователя 65 последовательного кода в параллельный подаваться на i-ю схему 62 исключающего ИЛИ справа или нет, в зависимости от того, равен ли соответствующий бит битовой последовательности hi+1 (1), hi+1 (2), …, hi+1 (N) ”1” или ”0” .
Вывод от процессора полиномиального умножения, показанный на фиг.8, находится в соответствии с выводом, формируемым операцией исключающего ИЛИ над выводами от N (=m-r) частей схем полиномиального умножения. Тогда как процессор полиномиального умножения, показанный на фиг.3, использует n(m-r) частей триггеров, процессор полиномиального умножения, показанный на фиг.8, использует n частей триггеров. Следовательно, параллельная конфигурация является эффективной для снижения числа триггеров, как показано на фиг.8.
На схеме, показанной на фиг.8, число веерных вставок в схемы 62 исключающего ИЛИ, расположенных между триггерами, больше, чем число веерных вставок в схемы 32 исключающего ИЛИ в схеме полиномиального умножения, показанной на фиг.4. Если максимальное число веерных вставок схем исключающего ИЛИ в схеме, показанной на фиг.8, превышает допустимый интервал, тогда число веерных вставок может быть сохранено в допустимом интервале с помощью расположения схем полиномиального умножения в параллельных и последовательных соединениях. Процессор полиномиального умножения, расположенный таким образом, эквивалентен процессору полиномиального умножения, показанному на фиг.3, где схема, показанная на фиг.8, добавлена вместо каждой из схем 21 полиномиального умножения.
Использование устройства кодирования с исправлением ошибок согласно вышеуказанным примерным вариантам осуществления описано ниже. Фиг.9 является примером расположения системы обмена данными, которая использует устройство кодирования согласно настоящему изобретению. Система обмена данными содержит устройство 81 передачи данных и устройство 85 приема данных для приема данных, переданных от устройства 81 передачи данных с помощью канала 80 связи. Устройство 81 передачи данных содержит устройство 82 кодирования согласно настоящему изобретению, которому предоставляются данные для передачи, устройство 83 синхронного управления и преобразования данных для осуществления синхронизации кадров по битовой последовательности, передаваемой от устройства 82 кодирования, и модулятор 84 для модулирования данных, передаваемых от устройства 83 синхронного управления и преобразования данных и отправки модулированных данных по каналу 80 связи. Устройство 82 приема данных содержит демодулятор 86 для демодулирования информации, принятой от маршрута 50 передачи, устройство 87 синхронного управления и преобразования данных для преобразования данных, передаваемых от демодулятора 86 в данные, которые необходимо ввести в устройство декодирования и обработки данных для синхронизации кадров, и устройство 88 декодирования для осуществления процесса повторного декодирования, например процесса декодирования суммы-произведения.
Конфигурация, показанная на фиг.9, может быть модифицирована в устройство хранения данных с помощью записи вывода от модулятора 84 на записывающий носитель вместо передачи вывода в канал 80 связи и предоставления информации, считываемой из записывающего носителя, а не из канала 80 связи в демодулятор 86.
Как описано выше, устройство кодирования с исправлением ошибок согласно настоящему изобретению допускает выполнение широкого диапазона требований в отношении длины кода, длины информационных битов и отношения кодирования (отношения увеличения полосы) с помощью выбора параметров m, r, n и полиномов.
Так как устройство кодирования с исправлением ошибок согласно настоящему изобретению содержит простую комбинацию схем полиномиального умножения и схем полиномиального деления, оно может иметь простую конфигурацию, может снижать объем вычислений, требуемых для кодирования данных и может также уменьшать размер устройства. Устройство кодирования с исправлением ошибок также допускает достижение большого коэффициента эффективности на основе повторного декодирования с помощью выбора соединений в схемах полиномиального умножения и схемах полиномиального деления. Настоящее изобретение, таким образом, содействует увеличению надежности и уменьшению требуемой электрической мощности систем связи.
ПРОМЫШЛЕННАЯ ПРИМЕНИМОСТЬ
Настоящее изобретение используется как технология исправления ошибок для выполнения системных требований для снижения мощности и выполнения антенн небольшого размера в системах спутниковой или сотовой связи или технология исправления ошибок, увеличивающая надежность запоминающих устройств, например магнитных записываемых запоминающих устройств.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОДИРОВАНИЯ, СПОСОБ ДЕКОДИРОВАНИЯ, КОДЕР И ДЕКОДЕР | 2014 |
|
RU2643506C2 |
| СПОСОБ КОДИРОВАНИЯ, СПОСОБ ДЕКОДИРОВАНИЯ, КОДЕР И ДЕКОДЕР | 2010 |
|
RU2532702C2 |
| СПОСОБ ПЕРЕДАЧИ ДАННЫХ | 2008 |
|
RU2448417C2 |
| УСОВЕРШЕНСТВОВАННЫЙ ПОДХОД К ДЕКОДИРОВАНИЮ m-МАССИВА И ИСПРАВЛЕНИЮ ОШИБОК | 2004 |
|
RU2380736C2 |
| УСТРОЙСТВО КОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК И СПОСОБ КОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК, ИСПОЛЬЗУЕМЫЙ В НЕМ | 2005 |
|
RU2373641C2 |
| Способ диагностики недвоичных блоковых кодов | 2018 |
|
RU2693190C1 |
| УСТРОЙСТВА И СПОСОБ СОГЛАСОВАНИЯ КЛЮЧЕЙ | 2018 |
|
RU2736109C1 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ, УСТРОЙСТВО ХРАНЕНИЯ ДАННЫХ, СИСТЕМА ОБМЕНА ДАННЫМИ И СПОСОБ ДЕКОДИРОВАНИЯ | 2008 |
|
RU2440669C1 |
| Система надежного облачного хранения с регулируемой избыточностью данных | 2021 |
|
RU2782681C1 |
| СПОСОБ И СИСТЕМА РАСПРЕДЕЛЕННОГО ХРАНЕНИЯ ВОССТАНАВЛИВАЕМЫХ ДАННЫХ С ОБЕСПЕЧЕНИЕМ ЦЕЛОСТНОСТИ И КОНФИДЕНЦИАЛЬНОСТИ ИНФОРМАЦИИ | 2017 |
|
RU2680350C2 |
Изобретение относится к способу и устройству блочного кодирования с исправлением ошибок, более конкретно к способу и устройству для кодирования с проверкой на четность с низкой плотностью. Способ кодирования с исправлением ошибок, использующий код с проверкой на четность с низкой плотностью, включающий: разделение информационной битовой последовательности, которую необходимо обработать для кодирования с исправлением ошибок, на (m-r) первых блоков, каждый из которых содержит битовую последовательность, которые имеют длину n и r вторых блоков, которые содержат соответствующие битовые последовательности, которые имеют длины k1, k2, …, kr; первая операция для осуществления полиномиального умножения на (m-r) первых блоков, выводящая r битовых последовательностей, которые имеют длину n; вторая операция для осуществления полиномиального деления и полиномиального умножения на r вторых блоков и r результатов операции первой операции, вывод битовой последовательности, включая избыточные битовые последовательности, которые имеют соответствующие длины n-k1, n-k2, …, n-kr. Технический результат - повышение эффективности кодирования. 4 н. и 7 з.п. ф-лы, 9 ил.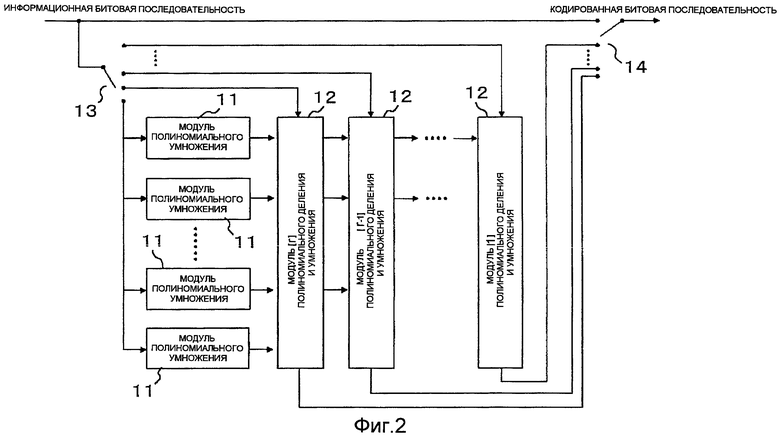
1. Способ кодирования с исправлением ошибок, использующий код с проверкой на четность с низкой плотностью, причем способ содержит
этап, на котором разделяют информационную битовую последовательность, которую необходимо обработать для кодирования с исправлением ошибок, на (m-r) первых блоков, каждый из которых содержит битовую последовательность, имеющую длину n, и r вторых блоков, содержащих соответствующие битовые последовательности, которые имеют длины k1, k2, …, kr, где m, n - положительные целые числа, r - целое число в интервале 1≤r≤m, и k1, k2, …, kr - целые числа в интервале 0≤k1, k2, …, kr≤n-1;
первую операцию для осуществления полиномиального умножения на упомянутые (m-r) первых блоков, и этап, на котором выводят r битовых последовательностей, имеющих длину n; и
вторую операцию для осуществления полиномиального деления и полиномиального умножения на упомянутые r вторых блоков и r результатов операции упомянутой первой операции, и этап, на котором выводят кодовую битовую последовательность, в которой комбинируют информационную битовую последовательность и избыточную битовую последовательность.
2. Способ согласно п.1, в котором упомянутая вторая операция содержит
первую операцию полиномиального деления и умножения для одновременного осуществления не более чем одного полиномиального деления и не более чем (r-1) полиномиальных умножений на второй блок, который имеет длину kr, и r результатов операции от упомянутой первой операции, и этап, на котором выводят (n-kr) битов и (r-1) битовых последовательностей, которые имеют длину n упомянутых последовательностей избыточных битов; и
р-ю операцию полиномиального деления и умножения, где p - целое число в интервале 2≤p≤r, для одновременного осуществления не более чем одного полиномиального деления и не более чем (r-p) полиномиальных умножений на (r-р+1) битовых последовательностей, которые имеют длину n, получаемых из (р-1)-й операции полиномиального деления и умножения, и на упомянутый второй блок, который имеет длину kr-p+1, и этап, на котором выводят (n-kr-p+1) битов и (r-p) битовых последовательностей, которые имеют длину n упомянутых последовательностей избыточных битов.
3. Способ по п.2, в котором делитель в операции полиномиального деления содержит частное полинома, полученное делением полинома хn-1 на полином, содержащий произведение минимальных полиномов в простом поле элементов конечного поля, включая n-й корень из 1.
4. Устройство кодирования с исправлением ошибок, использующее код с проверкой на четность с низкой плотностью, содержащее
блок деления для разделения информационной битовой последовательности, которую необходимо обработать для кодирования с исправлением ошибок, на (m-r) первых блоков, каждый из которых содержит битовую последовательность, имеющую длину n и r вторых блоков, содержащих соответствующие битовые последовательности, которые имеют длины k1, k2, …, kr, где m, n - положительные целые числа,
r - целое число в интервале 1≤r≤m, и k1, k2, …, kr - целые числа в интервале 0≤k1, k2, …, kr≤n-1;
r первых процессоров для осуществления полиномиального умножения на упомянутые (m-r) первых блоков, и для вывода битовой последовательности, имеющей длину n как результат операции, каждым процессором; и
второй процессор для осуществления полиномиального деления и полиномиального умножения на упомянутые r вторых блоков и результаты операции, соответственно, предоставляемые параллельно от упомянутых r первых процессоров, и для вывода кодовой битовой последовательности, в которой комбинируют информационную битовую последовательность и избыточную битовую последовательность.
5. Устройство по п.4, в котором упомянутый второй процессор содержит
первый модуль полиномиального деления и умножения для одновременного осуществления не более чем одного полиномиального деления и не более чем (r-1) полиномиальных умножений на второй блок, который имеет длину kr, и результаты операции от упомянутых r первых процессоров, и для вывода (n-kr) битов и (r-1) битовых последовательностей, которые имеют длину n упомянутых последовательностей избыточных битов; и
p-й модуль полиномиального деления и умножения, где p - целое число в интервале 2≤p≤r, для одновременного осуществления не более чем одного полиномиального деления и не более чем (r-p) полиномиальных умножений на (r-p+1) битовых последовательностей, которые имеют длину n, получаемых из (p-1)-го модуля полиномиального деления и умножения, и на упомянутый второй блок, который имеет длину kr-p+1, и для вывода (n-kr-p+1) битов и (r-p) битовых последовательностей, которые имеют длину n упомянутых последовательностей избыточных битов.
6. Устройство по п.4, в котором каждый из упомянутых первых процессоров содержит множество регистров, расположенных каскадом на множестве уровней; и
схемы «Исключающее ИЛИ», соединенные с соответствующими входными концами регистров в каскадном соединении,
при этом упомянутые схемы «Исключающее ИЛИ» имеют логические состояния вывода, установленные соединениями, определяемыми на основании заранее заданной полиномиальной операции таким образом, что логическое состояние вывода каждой из упомянутых схем «Исключающее ИЛИ» является неинвертируемым или инвертируемым.
7. Устройство по п.5, в котором r-й модуль полиномиального деления и умножения содержит не более чем одну схему полиномиального деления и не более чем (r-q) схем полиномиального умножения, где q - целое число в интервале 1≤q≤r.
8. Устройство по п.7, в котором упомянутая схема полиномиального деления осуществляет полиномиальное деление, используя делитель, который содержит частное полинома, получаемое делением полинома xn-1 на полином, содержащий произведение минимальных полиномов по простому полю элементов конечного поля, включая n-й корень из 1.
9. Устройство по п.5, в котором упомянутый первый процессор содержит
множество регистров, расположенных каскадом на множестве уровней, и
схемы «Исключающее ИЛИ», соединенные с соответствующими входными концами регистров в каскадном соединении;
при этом упомянутые схемы «Исключающее ИЛИ» имеют логические состояния вывода, установленные соединениями, определяемыми на основании заранее заданной полиномиальной операции таким образом, что логическое состояние вывода каждой из упомянутых схем «Исключающее ИЛИ» является неинвертируемым или инвертируемым.
10. Устройство передачи данных для модулирования входящих данных и передачи модулированных данных, содержащее устройство кодирования с исправлением ошибок по любому из пп.4-9 для осуществления кодирования с исправлением ошибок по входящим данным.
11. Устройство для модулирования входящих данных и записи модулированных данных, содержащее устройство кодирования с исправлением ошибок по любому из пп.4-9 для осуществления кодирования с исправлением ошибок по входящим данным; модулятор для модулирования данных; записывающее устройство для записи модулированных данных.
| JP 2004072130 А, 04.03.2004 | |||
| US 6895547 В2, 17.05.2005 | |||
| СИСТЕМА ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК | 1991 |
|
RU2007042C1 |
| US 6928602 В2, 09.08.2005 | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Способ работы теплообменного элемента | 1987 |
|
SU1456745A1 |
Авторы
Даты
2011-01-10—Публикация
2007-04-25—Подача