Изобретение относится к области аналоговой вычислительной техники.
Известен функциональный преобразователь f 5 содержащий линейный аналого-цифровой блок, соединенный с одним из входов сумматора, функциональный цифро-аналоговый блок, вход которого является входом преобразователя, а выход подключен ко второму входу сумматора, цифровой управляемый резистор, один вывод которого соединен с выходом линейного цифро-аналогового блока, другой - с шиной нулевого потенциала, а управляющий вход - с выходом функционального цифро-аналогового блока.
Его недостатком является низкая точность преобразования из-за наличия методической погрешности при кусочно-линейной аппроксимации.
Наиболее близким техническим решением к изобретению является функциональный преобразователь t2 ,содержащий выходной сумматор, выход которого является выходом преобразователя, нелинейный блок, первый выход которого .соединен с первым входам вы- ходногосумматора, а вход является- входом преобразователя, сумматор,пер вый вход которого соединен со входом нелинейного блока, блок памяти,управляющий вход которого соединен со вто рым выходом нелинейного блока, а выход - со вторым входом сумматора, масштабный блок, вход которого соединен с выходом сумматора, а выход со входом выходного сумматора, квадратор, включенный между выходом сумматора и входом выходного сумматора.
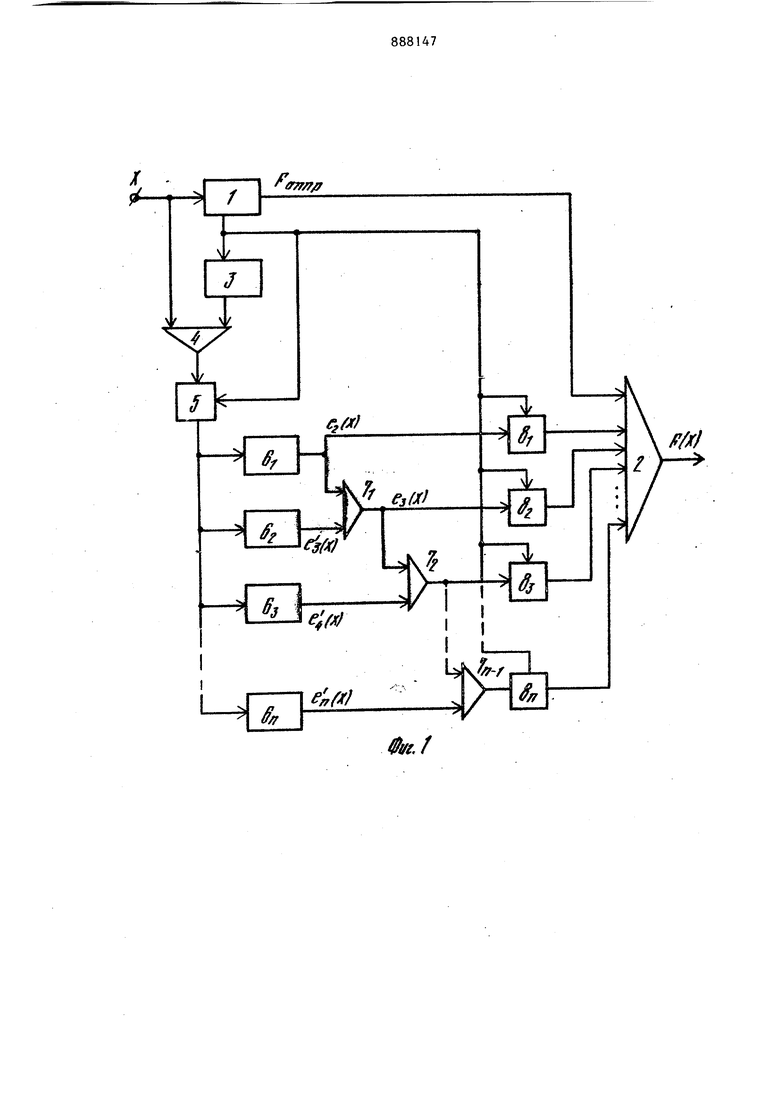
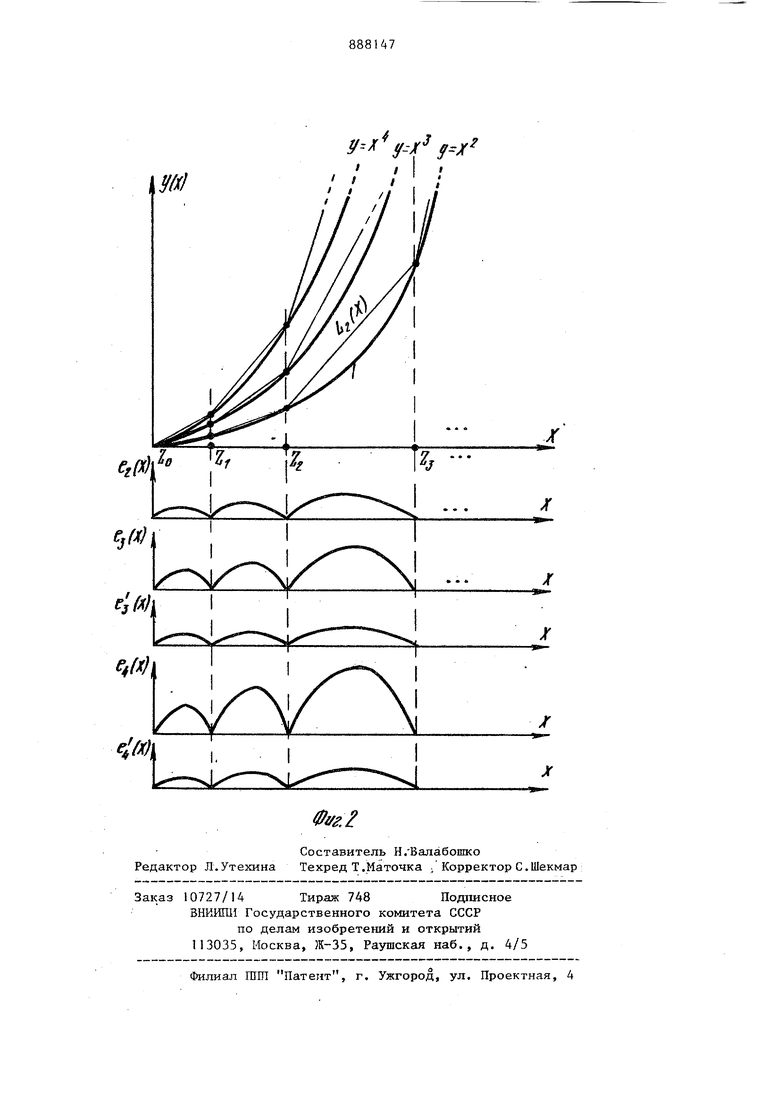
Такой преобразователь воспроизводит кйадратйчную функцию как сумму Кусочно-линейной аппроксимирующей функции и корректирующей функции,что позволяет устранить методическую погрешность. Его недостатком является то, что он воспроизводит только квадратичную функцию. 3 Целью изобретения является распш рение класса воспроизводимых функгщ Это достигается тем, что функцио нальный преобразователь, содержащий вькодной сумматор, выход которого является выходом преобразователя, нелинейный блок, первый выход котор го соединен с первым-,входом выхОдног сумматора, а вход является входом преобразователя, сумматор, первый вход которого соединен со входом нелинейного блока, блок памяти, упр ляющий вход которого соединен со вт рым выходом нелинейного Блока, а выход - со вторьм входом сумматора, масштабный блок, вход которого соединен с выходом сумматора, дополнительно содержит VI коррек тирующих нелинейных блоков, Vi-l дополнительных сумматоров, у дополнительных масштабных блоков, выходы к торых соединены со входами вьгхрдног сумматора, а управляющий вход - со вторым выходом основного нелинейног блока. Входы корректирующих- нелиней ных блоков соединены с выходом основного масштабного блока, управляющий вход которого соединен со вторым выходом основного нелинейного блока. Первый вход каждого дополнительного сумматора соединен с выходом предыдущего по номеру коррект рующего нелинейного блока, второй вход каждого дополнительного сумматора (. кроме первого 7 с выходом предьщущего дополнительного сумматора и с информационным входом со. ответствующего дополнительного мас штабного блока. Второй вход первого дополнительного сумматора соединен с выходом первого корректирующего нелинейного блока и с информационным входом первого дополнительного масштабного блока. Выход (Vi-l)-ro допо нительного сумматора с информационным входом У)-ГО дополнительйого масштабного блока. На фиг.1 приведена структурная схема преобразователя; на фиг.2графики, поясняющие принцип его ра- 50 боты. Преобразователь содержит нелинейный блок 1, выходной сумматор 2, блок памяти3, сумматор 4, масштабный блок 5, И корректирующих нели- .55 нейных блоков 6/j- бу, и И-1 дополнительных сумматоров 7| 7у ДО полннтельньгх 8у,. Преобразователь работает следующим образом. Для уяснения работы преобразователя кратно рассмотрим кусочно-динейную аппроксимацию функции V-X, где М7/2(см.фиг. 2 . Выберем узлы аппроксимации так, чтобы они образовывали геометрическую прогрессию. Если известны Х Уу„д наименьшее и наибольшее значения, которые принимает аргумент X то динамический диапазон представления аргумента в децибеллах равен 1 ч-201(Х,ахМм1У1)Запишем значения аргумента в узлах аппроксимации, обозначив их через Z. , г-Я 7 -Of Z - С} Z k k.-i Ч о, где q,основание геометрической прогрессии;К - число участков кусочно-линейной аппроксимации. Тогда очевидно В. , поэтому по заданным двум значениям К и Dr можно определить параметр с. Требования для выбора К будут определены ниже. Рассмотрим разность между функцией - Х и ее йусочнолинейной аппроксимацией (.так называемую функцию коррекции (х))для двух произвольных соседних участков ..,--IVi,Z), м ,,Здесь Хуу,и текущие значения аргумента на Ry. Тогда у1.(уг,-- 1 --Ьу„(х,„)(Хж), Ш. . VW«-1 VM-f/( ПИ-1 w-f/t Из рйссмотрения формул 1 и 2 видно, что если положить JfniVr где ( СОУ1 «at 7I и определено вьпае, то ( lb(w nitXm1 Vbv, U,) 5 vyibb.{Xyy,)), y.,..),(w,.r,( Из формулы (3 } видно, что для любых смежных участков кусочно-линей ной аппроксима1щй функции коррекции Ву,)5 vn + i СХлщ)подобны между собой. Чтобы получить значение Vr,..j (ги + |) Д текущего .,нужно отмасштабировать его с коэффициентом 1/(, подставить в В()и затем отмасштабировать функцию коррекции с коэффициентом ( Важно то, что для выбранного расположения узлов аппроксимации величины масштабирующи коэффициентов постоянны, что упрощае реализацию преобразователя. Запишем теперь функцию, воспроизводимук преобразователемР(х)-%±о| у±о12Х ±...±а„х С4) функции Х, И 7/- 2 представим в виде суммы кусочно-линейной аппрокси .мации и функции коррекции (.,т.,.е,,,-), |/CbiX b.-m,,,-.e,-), ( .-е,.) где - коэффициент масштабировани функции коррекции для фзгнкгщи у х на 1 -м участке кусочнолинейной аппроксимации. Подставим выражение 15 7 в выражение (4 , полу чим РЫ) tq |(с.,Х-Ъ,,)±. 3l|(),I b,(. 1-Ы|Л1 а1)-°зЙЛ е -)- V 4|rv)ЧФ ЭД--W-1 i Первое слагаемое в формуле C6J представляет собой кусочно-линейную аппроксимацию функции F(x), которая рассчитывается заранее,и на нее настраивается нелинейный блок 1. Хотя коэффициенты , УП,,- ,...., VTly,,j для каждой степенной функции зависят от номера л участка аппроксимации, одна 474 ко ввиду подобия корректирующих функций о/ношение этих коэс фициентов для соседних участковM JiTi rcOhstОчевидно TaKjjce, что домножение на коэффициенты полинома а, Q ,.. . 0|и не влияют на подобие корректируюпц-ix функций. .Рассмотрим теперь работу функционального преобразователя. Входная величина У поступает на нелинейный блок 1, который вырабатывает aппpoкcимнp:;,oщyю функцию подает ее на выходной сумматор 2. Кроме того, нелинейный блок 1 управляет блоком памяти 3, который подает на сумматор 4 значение очередного узла аппроксимации 2,. На выходе сумматора 4 образуется приращение аргумента , которое масштабируется блоком 5 и поступает на входы корректирующих нелинейных блоков 6 - 6 . Первый корректирующий блок 6i настро ен на функцию 2.-2 ) (см.фиг.2). Если рассмотреть значения 6 Х Ь- (it) для j 2, то можно легко установить, что ll, i у --- Поэтому второй нелинейный блок 6 настроен на воспроизведение функции -Ед 8о,, третий блок 6 на воспроизведемте функции ф (см.фиг.2 В этом случае требоваш-1Я по точности к корректирующим нелинейным блокам 6, бу, значительно снижаются. Например, пусть, исходя из требований простоты, стабильности и т.д. в нелинейном блоке 1 воспроизводится К кусочно-линейных участков, в результате чего достигается точность в 1% для функции ) 2% для У Х Пусть корректирующий нелинейный блок 6 воспроизводит функцию Ki(f) с погрешностью 10%, тогда результирующая погрешность для функции X равна 0,1%. Чтобы получить такую же результирующую погрешность для функции V Х необходимо уметь воспроизводить корректирующую функцию (Е,(Х) вдвое точнее, чем для V нашем случае воспроизводится разность B iX -BaU; 2% - 1% %, поэтому удвоение точности не требуется. Таким образом, последовательное использование предшествующих функций коррекции для получения последующей позволяет упростить корректирующие
нелинейные блоки 6.( г6 и повысить точность преобразования.
Полученные корректирующие функции затем масштабируются в соответствии с формулой (3) в масштабных блоках 8 - 8 у, и суммируются со своими знаками в выходном сумматоре 2 с аппроксимирующей функцией, на выходе которого образуется результат преобразования в виде формуль ( 4 ).
.Достоинствами предлагаемого функционального преобразователя являются отсутствие методической погрешности, простота, так как, во-первых, корректирующие нелинелинейиые блоки 6,j -бу. могут быть простыми и сравнительно грубыми, во-вторых, набор узлов аппроксимации один и тот же для всех степенных функций, что упрощает реализацию блока памяти 3.
Предлагаемый преобразователь может быть использован при моделировании различных функциональных зависимостей, которые приближенно мож но представить степенным полиномом/, и поэтому воспроизводит более широкий класс функций, чем прототип.
Формула изобретения
Функциональный преобразователь, содержащий выходной сумматор, выход которого является выходом преобразователя, нелинейный блок, первый выход которого соединен с первым входом выходного сумматора, а вход является входом преобразователя, сумматор, первый вход которого соединен со входом нелинейного блока, блок памяти, управляющий вход которто соединен со вторым выходом нелинейного блока, а выход - со вторым входом сумматора, масштабный блок, вход которого соединен с выходом сумматора, отличающийся- тем,
что, с целью рас1Ш1рения класса воспроизводимых функций, он содержит ц корректирующих нелинейных блоков, VI-1 дополнительных сумматоров, И дополнительных масштабных блоков, выходы
которых соединены со входами выходного сумматора, а управляющий вход со вторым выходом основного нелинейного блока,входы корректирующих нелинейных блоков соединены с выходом
основного масштабного блока, управляющий вход которого соединен со вторым выходом основного нелинейного блока, первый вход каждого из дополнительных сумматоров соединен с выходом предыдущего по номеру корректирзпощего нелинейного блока, второй вход каждого из дополнительных сумматоров, кроме первого, соединен с выходом предыдущего по номеру дополнительного сумматора и с информационным входом соответствующего дополнительного масштабного блока, второй вход первого дополнительного сумматора соединен с выходом первого корректирующего нелинейного блока и с информационным входом первого дополнительного масштабного блока, выход (И)го дополнительного сумматора соединен с информационным входом И-го дополнительного масштабного блока.
Источники информации, принятые во внимание при экспертизе
1. Авторское свидетельство СССР № 3778ОбТ кл. G 06 G 7/24, 1974. 2. Авторское свидетельство СССР № 550650, кл. G 06 G 7/20, 1977 (прототип) .
////



| название | год | авторы | номер документа |
|---|---|---|---|
| Квадратор | 1978 |
|
SU807333A1 |
| Квадратичный преобразователь | 1980 |
|
SU934496A1 |
| Квадратичный функциональныйпРЕОбРАзОВАТЕль | 1978 |
|
SU805347A1 |
| Функциональный преобразователь | 1980 |
|
SU883923A1 |
| Устройство для извлечения квадратного корня | 1976 |
|
SU570068A1 |
| Функциональный преобразователь | 1980 |
|
SU881772A1 |
| Устройство для вычисления функции двоичной экспоненты | 1985 |
|
SU1305675A1 |
| Функциональный преобразователь | 1980 |
|
SU934502A1 |
| Функциональный преобразователь | 1979 |
|
SU849241A1 |
| Устройство для вычисления функций у=aRcSINx и у=aRccoSx | 1980 |
|
SU935949A1 |


Авторы
Даты
1981-12-07—Публикация
1980-03-17—Подача