(54) СПОСОБ ЦЕНТРОБЕЖНОЙ ОБРАБОТКИ ШАРИКОВ


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для центробежной обработки шариков | 1979 |
|
SU899329A1 |
| Способ упрочняюще-чистовой обра-бОТКи и уСТРОйСТВО для ЕгО ОСу-щЕСТВлЕНия | 1979 |
|
SU841936A1 |
| Инструмент для упрочняюще-чистовой обработки поверхностей | 1975 |
|
SU657981A1 |
| Способ обработки шариков и станок для его осуществления | 1986 |
|
SU1440672A1 |
| СПОСОБ УЛЬТРАЗВУКОВОЙ ГИДРОДИНАМИЧЕСКОЙ ОЧИСТКИ ПОВЕРХНОСТЕЙ ИЗДЕЛИЙ | 2010 |
|
RU2427433C1 |
| СПОСОБ ГРАВИТАЦИОННОЙ ГЕМОРЕАБИЛИТАЦИИ КОСМОНАВТОВ В УСЛОВИЯХ НЕВЕСОМОСТИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2020 |
|
RU2757577C1 |
| Способ очистки зернового вороха и устройство для его осуществления | 1987 |
|
SU1517834A1 |
| СПОСОБ ЦЕНТРОБЕЖНОЙ ОБРАБОТКИ ВНУТРЕННИХ ПОВЕРХНОСТЕЙ МЕЛКОРАЗМЕРНЫХ ДЕТАЛЕЙ | 2014 |
|
RU2572684C1 |
| УСТРОЙСТВО ДЛЯ ТОКАРНОЙ ОБРАБОТКИ ПАКЕТА ПОРШНЕВЫХ КОЛЕЦ | 1993 |
|
RU2014896C1 |
| СПОСОБ РАЗДЕЛЕНИЯ СЫПУЧИХ МАТЕРИАЛОВ ПО МАССЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1994 |
|
RU2085304C1 |


1
Изобретение относится к абразивной обработке и может быть использовано в шарикоподшипниковой промышленности.
Известен способ обработки шариков, при котором шарикам, расположенным в полости между двумя вращающимися рабочими инструментами выполненными в виде дисков, сообщают вращение, воздействуя на них средой под давлением, Направленной тангенциально поверхностям рабочих инструментов, ограничивающих полость по периферии.
Такой способ обработки увеличива-. ет подвижность шариков относительно рабочей поверхности инструмента ll.
Однако способ не обеспечивает шарикам вращения вокруг оси, совпадающей с вектором скорости центра. За один оборот шарика вокруг оси инструмента не обеспечивается контактирование всей его обрабатываемой поверхности с рабочей поверхностью инструмента. Качество обработанной поверхности и производительность такого способа не удовлетворяют требованию современного производства.
Наиболее близким к изобретению по технической сущности н достигаемому 1юзупьтату является способ обработки шариков, iipH котором давление воздействующей на шарики среды периодически изменяют от минимального до максимального значений по синусоидальному закону с периодом, равным времени оборота шарика вокруг оси рабочих инстру, ментов .
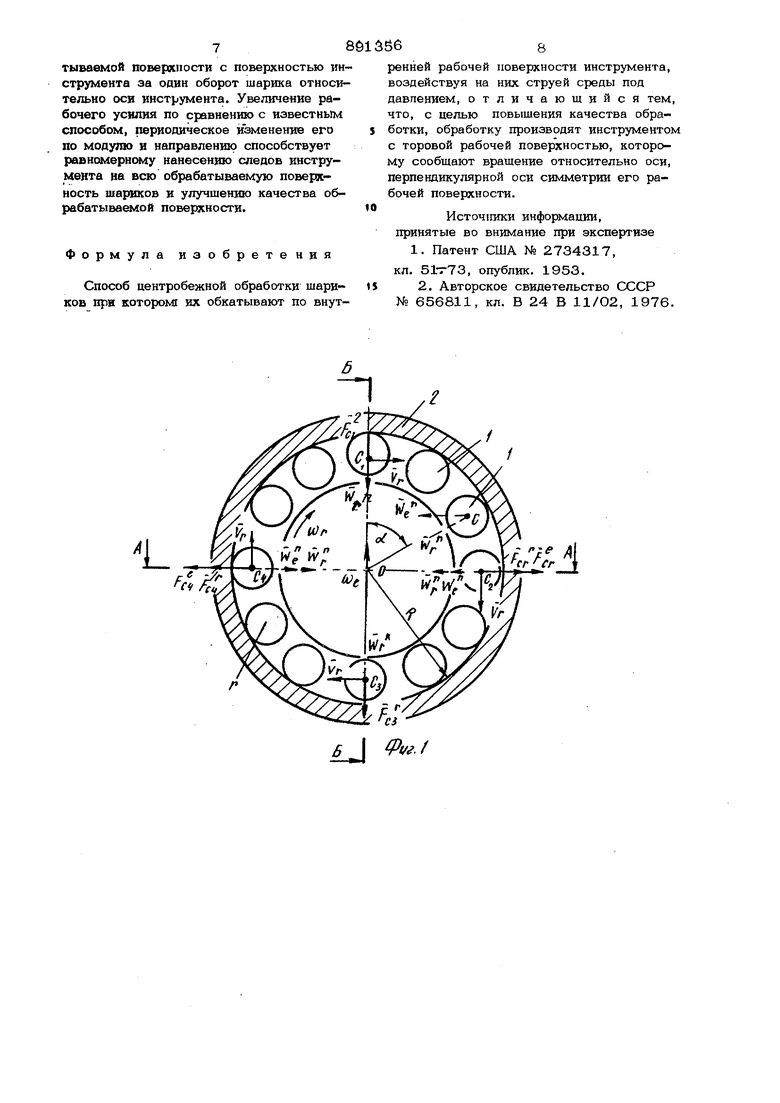
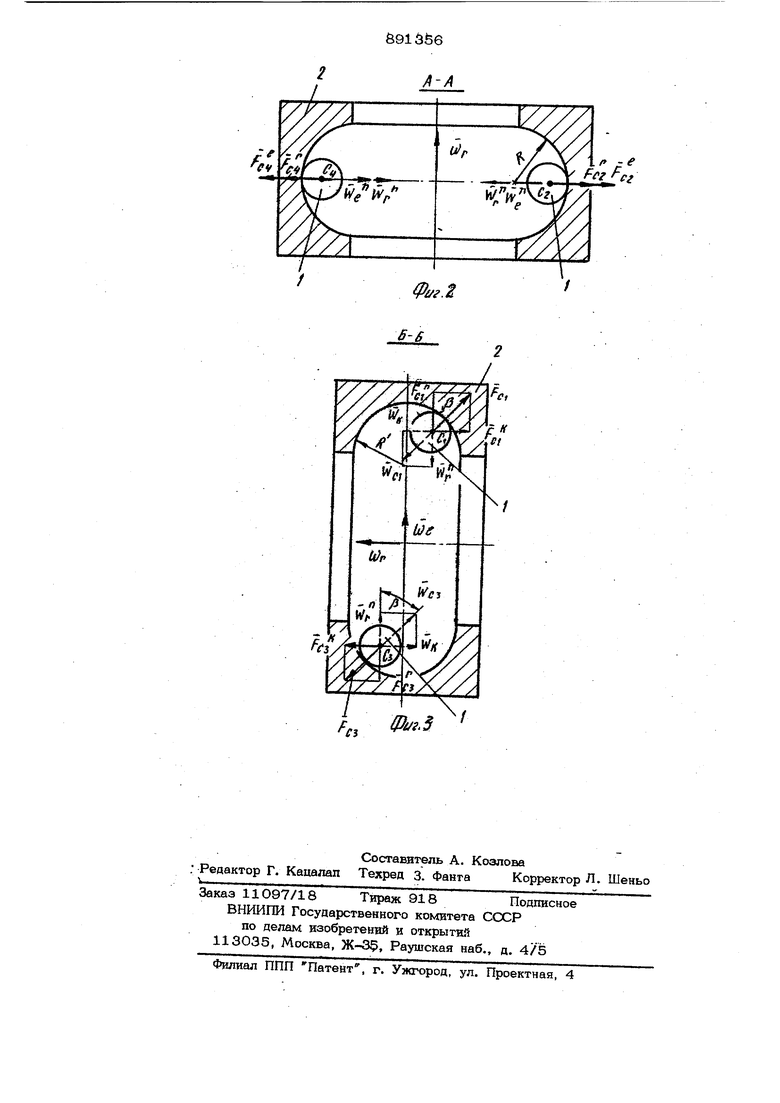
Недостатком известного способа является низкое качество обрабатываемой поверхности шариков, вызванное тем, что периодическое измечение давления приводит к изменению только величины вектора скорости центра, направление же движения шариков остается постоянным, т.е. гарантированного изменения положения опорных точек на обрабатываемой поверхности не происходит. Вращение шариков вокруг оси, совпадающей с вектором скорости центра, про тсходит под действием случайных факторов, траектория центра шарика лежит в одной плоок ости. Цель изобретения - улучшение качества обработанной поверхности., Поставленная цель достигается тем, что инструмент с торовой рабочей по- верхностью врашают относительно оси, перпендикулярной оси симметрии его внутренней торовой рабочей поверхвоНа фиг. 1 представлена схема, поясня ющая движение шариков вдоль рабочей поверхности инструмента; на фиг. 2 -раз рез А-А на фиг. 1:, на фиг. 3 - разрез Б-Б на фиг. 1. Шарики 1 (фиг. 1) вращаются со ско ростью (Dj- под действием струи среды, под давлением исходящей из тангенциаль ных сопел (на показаны) так, что вектор угловой скорости Ш совпадает с осью симл-гетрии внутренней торовой рабочей поверхности инструмента 2. Инструмент 2 вращают при этом с угловой скоростью JtJe вокруг оси, перпендикуляр ной оси симметрии его внутренней торов рабочей поверхности. В данном случае о вращения инструмента 2 лежит в плоско Tji: чертежа и вертакальна (фиг. 1 и 2) так, что зекторы ( и (S) перпендику™ лярньг. Такиь1 образом, обрабатываемые шар1П и 1 участвуют в двух вращательных двкж.епиях - относительно рабочей поеерхкости инструмента и вместе с ней. При равномерном относительном и переносном вращениях центры шариков 1 им ют ускорение , Wg ШеОС-SIvncL-норм льное ускорение в переносном движении. Вектор направлен к центру переносного вращегога, т.-е. перпендикуля но оси вращения инструмента. Максимал ное значение ускорения g будет пр ot 90, 270 450 и т.д.; минимал ное - при ot О, 180 „ 36О и т.д., т.е. Wg Cnioi)-ayg(.), (2 где R наибольший радиус внутренней рабочей поверхности инструмента;V - радиус обрабатываемых шари ков. Нормальное ускорение в относительном движении определяется из выражения (R-)J:rCons-b (3 Ускорение Кориолиса ))( Vy, модуль 2aeV 5in Vy.) в нашем случае вектор {J/g лежит в плоскости чертежа (фиг. 1 и 2). Вектор скорости центра шарика в отдельном движении у также лежит в плоскости чертежа и меняет свое направление в зависимости от значения угла di . Таким образом, вектор (i всегда перпендикул рен плоскости чертежа и направлен от нас для шарика, занимающего положение С/| (фиг. 1), и к нам - цля шарика, занимающего положение С Д аксимальное значение, вектора W| будет при 51И (CWgAVj,)- -t, когда (Jfg 1 Vj. , т.е. при oi 0, 180,360 и т.д.; минимальное - при 6iyi(.)-)-O когда Oug II Vy , т.е. при , 270, 450° и т.д. Таким o6pa30M,05W, 2a/g ) w(niax:)-2c«;g().. Таким образом, максимальное значение ускорения Кариолиса- будет при наличии минимального (равного нулю) нормального ускорения Б переносном движении шарика и наоборот. Подставив выражения (2) - (4) в уравнение (1) находим максимальные значения полного ускорения за время полного оборота шарика вокруг Оси инструмента. При ot 0 ° и оС 1 80 ° Vcwp) (5) c65p rco6p.3 cosfb w /Wc.|. (е) При и 270 C2-- CV---(VV,C,X) ((К)(7) Подставляя в выражения (5) и (6) значения соответствующих величин из уравнений (3) и (4), получаем I , rCR)Vcu -v4ui;| , С06р -COS))-COSfb T/u; -1- 4«;е Для удобства количественного сравнения известного способа с предложенным положим WQ IV оу , тогда известный 56 способ обеспечивает максимальное ускорение,)cone-b, (10 так как в известном способе {ц) 0 и поэтому 0 (формулы 2 и 4) Из уравнения (7) видно, что предлагаемый способ обеспечивает в двух противоположных положениях шарика следующую величину ускорения: )(11) Из уравнения (8) видно, что предлагаемый способ в двух других противоположных положениях шарика обеспечивает - «(R-h) 2,IV/ Согласно второму закону Ньютона сила F - VnW, где Уи -масса шарика. Таким образом, известный способ обеспечивает постоянную по величине силу инерции расположенную в плоскости вращения -цент ров шариков, (уравнение 10) vnax yyiax CR-r)--con t j Предлагаемый способ обеспечивает переменные силы по модулю и направлению. Причем макс11мальное значение сил, действующих на обрабатываемые шарики, бо льше, чем в известном способе. Так, сог ласно второму закону Ньютона, из уравнений (11) и (12) находим -2F С2.С4 тах (14)/ 2,( (15) В связи с тем, что сила F действует в направлении, перпендикулярном плос кости, в которой расположены векторы (JWg и } , а центробежные силы инерции в относительно движении и F лежат в плоскости чертежа (фиг. 1 и 2), суммарные силы определятся из выражений- F t F ci С1 Сл-с (16 г - сГ . г (17) Силы инерции F направлены по углом р к оси вращения инструмента (фиг. 2), что приводит к обкатыванию ша рика по рабочей поверхности инструмента к продольном сечении. Это способствует гарантированному изменению положения опорных точек на обрабатыр аемой поверх ности. При дальнейшем апижентга шарика по рабочей поверхности в поперечном сечеirros (фиг. 1), при о/- 90- F.,0, а сила 6 инерции FCO. равна ари(}метической сумме сил и F,2 . Шарик в этом положении находится в диаметральной плоскости торовой рабочей поверхности инструмента (фиг. 3). Fe 0 сила Кориолиса имеет максимальное значение, однако направлена она в сторону, противоположнук) по сравнению с положением щарика при . Шарик при этом откатывается по рабочей поверхности инструмента в продол ном сечении (фиг.2) в противоположном направлении, отклоняясь на тот же угол /. oi.270° F При oi. 270 Р.. 0, а глС +Fc4 Диаметральная плоскос-гь шарика при этом совпадает с диаметральной плоскостью торовой поверхности инстру- мента. периодичность деист- ВИЯ сил инерции повторяется. Как видно из формулы (9), угол р , характеризуюший отклонение шарика от круговой траектории (искривление его траектории), не зависит от размеров инструмента и диаметра обрабатьшаемых шаршсов. При условии ji)Q CftJj, cw из уравнения (9) имеем cosfe- --- covis (18) Из уравнения (18) видно, что угол наклона векторов сил и не зависит от кинематических характеристик способа, размеров инструмениа и диаметра обрабатываемых шариков. -Величина угла составляет около 60. Таким образом, . легко добиться поворота шариков под действием силы FX , обеспечиваюшего расположение опорных точек по всей обрабатываемой поверхности шарика за один оборот его вокруг оси инструмента, путем изменения скорости вращения последнего. Радиус внутренней рабочей поверхности инструмента в продольном сечении (фиг. 2 и 3) выбирается из условия возможности поворота обрабатываемого шаржа радиуса Г под действием силы Кориолиса на угол не менее 1 ВО в одну сторону. Поэтому длина полуокружности рабочей поверхности инструмента должна быть равна 2 ,а радиус Р 2 1. Таким образом, при обработке шариков с сообщением им обкатывания под действием среды под давлением под внутренней тороидальной рабочей поверхности . инструмента, , вращаюигегося вокруг оси, перпендикулярной оси симметрии его рабочей поверхности, обеспечивается гарантированное соприкосновение всей обрабатываемой поверхности с поверхностью ин струмента за один оборот шарика относительно оси инструмента. Увеличение рабочего усилия по сравнению с иэвестнь М способом, периодическое изменение его по модулю и направлению способствует равномерному нанесению следов инструмента на всю обрабатываемую поверхность шартосов и улучшению качества обрабатываемой поверхности.
Формула изобретения
Способ центробежной обработки шариков при котором их обкатывают по внут L
/Й
ij ренней рабочей поверхности инструмента, воздействуя на них струей среды под давлением, отличающийся тем, что, с целью повышения качества обработки, обработку производят инструментом с торовой рабочей поверхностью, которому сообщают вращение относительно оси, перпендикулярной оси симметрии его рабочей поверхности.
Источ1гаки информации, принятые во внимание при экспертизе

Авторы
Даты
1981-12-23—Публикация
1979-12-06—Подача