(54) ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для спектрального анализа | 1981 |
|
SU1013972A1 |
| Цифровой анализатор энергетического спектра | 1978 |
|
SU769443A1 |
| Устройство для выполнения преобразования Фурье | 1985 |
|
SU1278887A1 |
| Цифровой анализатор спектра | 1979 |
|
SU798615A1 |
| Устройство для вычисления коэффициентов обобщенных дискретных функций | 1978 |
|
SU752347A1 |
| Генератор случайного процесса | 1982 |
|
SU1068935A1 |
| Устройство для формирования случайных процессов с заданным спектром | 1981 |
|
SU1027723A1 |
| Способ воспроизведения случайной вибрации с заданным спектром плотности мощности и устройство для его осуществления | 1988 |
|
SU1518691A1 |
| Генератор случайного процесса | 1981 |
|
SU972505A1 |
| ГЕНЕРАТОР СЛУЧАЙНОГО ПРОЦЕССА | 1991 |
|
RU2050585C1 |

Изобретение относится к вычислительной технике и, в частности, к устройствам и системам вероятностного цифрового моделирования процессов и динамических систем, и позволяет получать гауссовые случайные числа с заданным энергетическим спектром.
При решении многих задач анализа и синтеза динамических систем широко применяют цифровое вероятностное моделирование. В этом случае на вычислительном устройстве не только моделируется исследуемый объект, но и формируется внешнее возмущение на этот объект. Как правило, внешнее возмущение представляет собой стационарный случайный процесс с известным энергетическим спектром.
Известно устройство генерации гауссовых случайных чисел с заданным энергетическим спектром (или с заданной автокорреляционной функцией) fl.
Однако это устройство не может формировать случайные гауссовские числа с произвольно заданной формой спектра. Для формирования заданного энергетического спектра последовательности гауссовых случайных чисел
используют метод канонических разложений.
Однако этот период требует очень больших вычислительных затрат. В С23 предложен эффективный способ формирования гауссовых случайных чисел с заданным энергетическим спектром, основанныйна применении метода быстрого преобразования Фурье и вычисле10нию канонического разложения гауссова случайного процесса. Этот метод заключается в вычислении дискретного преобразования Фурье от последовательности равномерно распределен15ных случайных чисел, взятых с весами, определенными частотной характеристикой формирующего фильтра.
Наиболее близким техническим решением к изобретению является устрой20ство, построенное на базе метода быстрого п$)еобразования Фурье, которое содержит тактовый-генератор, к первому выходу которого подключены последовательно соединенные
25 генератор равномерно распределенных чисел, перемножитель, блок буферной 1ИМЯТЙ и блок быстрого преобразования Фурье, 4 ко второму выходу подсоединен управляющий вход блока вы30борки, на 5 ервый вход которого включен первый блок резисторов памяти, а выход соединен со вторым входом перемножителя 2 .
При работе прототипа по сигналам тактового генератора формируется одно равномерно распределенное число (и общем случае комплексное) и осуществляется выборка из первого блока регистров памяти очередного значения весового коэффициента (также в общем случае комплексного). В перемножителе эти два числа перемножаются, а результат записывается в буферную память. На следующих тактах работы тактового генератора указанная процедура повторяется до тех пор пока не заполнится вся буферная память, содержащая № регистров. После заполнения буферной памяти включается в работу блок быстрого преобразования Фурье, на выходе которого формируется последовательность гауссовых случайных чисел с заданным эне гетическим спектром. Для успешной работы прототипа значения весовых коэффициентов должны быть пропорциональны корню квадратному из значений энергетического спектра на соответствующих частотах.
Несмотря на то, что устройствопрототип является наиболее быстрым из известных устройств генерации гауссовских случайных чисел с произвольно заданным спектром, вычислительные затраты в нем достаточно велики. Эти затраты составляют для последовательности из N rayccoBbiix чисел примерно комплексных арифметических операций сложения N(l+l/2 og N) комплексных операций умножения. Недостатком прототипа, . таким образом, является большой объем вычислительных затрат (малое быстродействие) при генерации гауссовых случайных чисел с заданным энергетическим спектром.
Цель изобретения - повышение быстродействия устройства.
Цель.достигается тем, что в известный генератор случайных чисел, содержащий генератор тактовых импульсов, первый выход которого соединен со входом генератора равномерно распределенных случайных чисел, выход которого соединен с первым входом блока умножения, второй вход которого подключен к выходу ключа, выход блока умножения соединен со входом первого блока памяти, второй блок памяти, введены блок формирования весовых коэффициентов, блок быстрого преобразования Уолша и элемент задержки, вход которого подключен ко второму выходу генератора тактовых импульсов, третий выход которого соединен со входом блока формирования весовых коэффициентов.
группа входов которого соединена с группой выходов второго блока памяти соответственно, выход блока формирования весовых коэффициентов соединен с информационным входом ключа управляющий вход которого подключен к выходу элемента задержки, выход первого блока памяти соединен со входом блока быстрого преобразования Уолша, выход которого является выходом генератора.
Кроме того, блок формирования весовых коэффициентов содержит два блока памяти, два коммутатора, квадратор, сумматор, нелинейный преобразователь и умножитель, группа выходов первого блока памяти соединена с группой входов первого коммутатра соответственно, вход которого объединен со входом второго коммутатора и является входом блсгка, группой входов которого является группа входов второго коммутатора, выход которого соединен с первым входом умножителя, выход которого соединен со входом второго блока памяти, выход которого является выходом блока, выход первого коммутатора через последовательно соединенные квадратор, сумматор и.нелинейный преобразователь соединен со вторым входом умножителя.
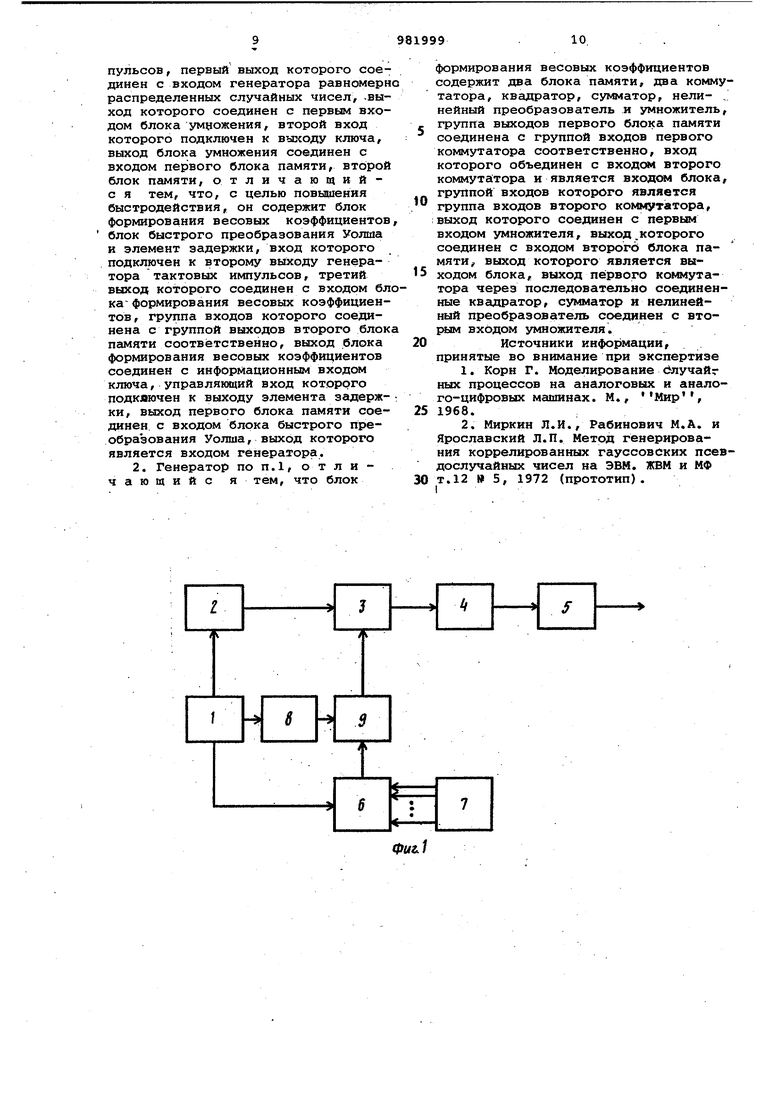
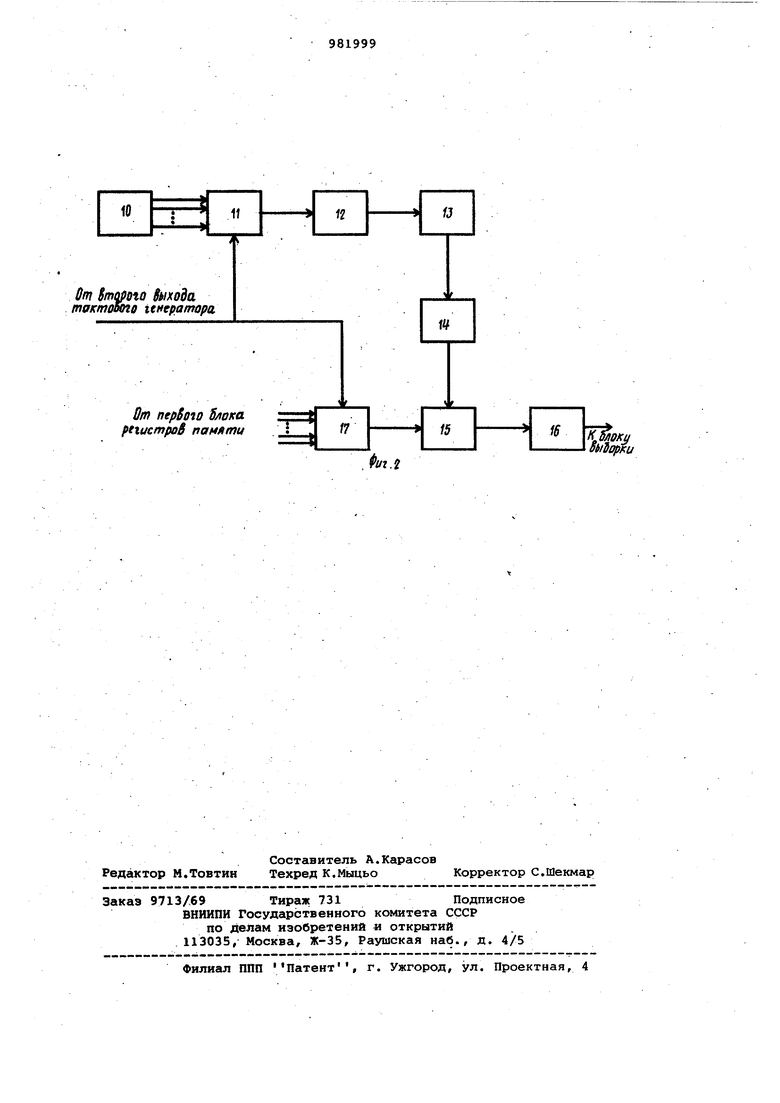
На фиг.1 приведена блок-схема предлагаемого генератора случайных чисел с заданным энергетическим спектром; на фиг.2 - схема блока формирования весовых коэффициентов.
Устройство содержит генератор 1 тактовых импульсов, к первому выходу которого подключены последовательно соединенные генератор равномерно распределенных случайных чисел 2, блок умножения 3, первый блок памяти 4 и блок быстрого преобразования Уолша 5. Второй выход генератора 1 соединен с управляющим входом блока формирования весовых коэффициентов 6, на информационные входы которого подключены выходы второго блока памяти 7. Третий выход генератора 1 через элемент задержки 8 подсоединен к ключу 9. Блок формирования весовых коэффициентов б состоит из последовательно соединенных первого блока памяти 10, первого коммутатора 11, квадратора 12, сумматора 13, нелинейного преобразователя 14, выполняющего извлечение квадратного корня из входной величины, умножителя 15 и второго блока памяти 16. На второй вход умножителя 15 включен выход второго коммутатора 17. Второй выход генератора 1 подключен к управляющим входам коммутаторов 11 и 17, а на входы второго коммутатора 17 включены выходы блока памяти 7. Выход блока памяти 16 подключен ко входу клю ча 9 . Генератор работает следующим образом. По сигналам генератора 1 в генератор 2 генерируются случайные независимые равномерно распределенные числа, которые поступают на первый вход блока умножения 3. Сигналы тактового генератора поступают также на управляющий вход блока формирования весовых коэффициентов б. По этому сигналу в блоке б формируется очередной весовой коэффициент, к торый ключом 9 по сигналу тактового генератора 1 отправляется на второй вход блока умножения 3. Элемент задержки 8 введен для того, чтобы сиг лы тактового генератора 1 поступали на ключ 9 только после того как в блоке б закончилось формирование очередного весового коэффициента. Для пояснения работы устройства приведем математическое обоснование его работы. Пусть F(Z) обобщенное дискретное преобразование. Фурбе взв шенной последовательнЬсти N комплексных случайных ограниченных и независимых -величин Z , К 0,1,..., N-1 -f N-1 . (1 f 2 Ph-VX-YR..K .5, л - последовательность весовых коэффициентов; ,K - полная, ортонормированн система базисных функц при разложении последо вательности f в обобщенный ряд Фурье. в 2} показано, что если i(n,k)exp(- -:r система дискретных экспоненциальных функций-,n,,l,.. N-1, ТО функция распределения случайных величин f, п 0,1,...,N -1 сходится к функции гауссовского закона, как О (I/YN). Автокорреляционная функция после довательности р. I равна: orM.g-Tlf. (2 -PuPwi- N (uo , ,1,...,Ы-1 Значения L имеют физический смысл отсчетов энергетического спектра. В предлагаемом устройстве вместо дискретного преобразования Фурье используется дискретное преобразование Уол1иа. При этом ст;авится и решается задача получения последовательности гауссовых случайных величин с энергетическим спектром j L J К 0,1,...,N-1 или, чтотоже, с корреляционной функцией R(C). Разложим последовательность p по базису дискретных экспоненциальных функций на интервале fO, N-lJ и по базису дискретных функций Уолша ), где коэффициенты разложения представлены в виде p(K) и f,) соответственно. Известно, что спектральные коэффициенты разложения связаны друг с другом соотношением ро()15(и)ФСИ,1с), И-0 ФЦЮ-- г1 9(.))- (5) Vrt О Функция называемая ядром Фурье. Ядра Фурье составляют ортонормированную систему функций ,К)Ф(П1,К)-- |j если m п О если m f п Из (4) имеем . /Sa(K) i 1Ч,(р)Ф (p,K)ts)f (е)ф(е,к) Г(р)5(е)Ф(р,к),Ю---|; 15др),к)/ Усредняя последнее равенство по множеству получаем р,(.к 11СкТ|--|гОО| (к)(ф(Р,К)| (8) Откуда связь между отсчетами частотной характеристики формирующего фильтра в базисе дискретных экспоненциальных функций и дискретных функций Уолша получим в виде (b(K)WlV(K)|0Cp.K)f Для практической работы более удобным является задание L значений частотной характеристики формирующего фильтра в привычном для инженера базисе экспоненциальных функций. Эти значения хранятся в блоке памяти 7. Вычисление весовых коэффициентов f) (к) необходимо выполнить только один раз. Поэтому, их можно считать заданными и пренебречь вычислительными затратами на их получение. Оценим выигрыш в числе арифметит ческих операций, даваемый предлагаемым устройством, при генерации . N гауссовских случайных чисел со значениями энергетического спектра L(K). Как указано выше, вычислительные затраты в прототипе составляют примерно N комплексных операций сложения и N( N) комплексных операций умножения. Более удобно, перейти к арифметическим операциям над действительными числами. При работе прототипа необходимо, реализовать примерно 2N+3Nfog2 N арифметических операций сложения и 2N(2+gog N) арифметических операций умножения (с учетом того обстоятельства, что
L I- последовательность
действительных чисел ClZ -X|... последовательность комплексных чисел). В предлагаемом устройстве комплексная последовательность случайны чисел Z, К 0,lf...,N-l умножается соответственно на действительные числа . На это требуется 2N операций умножения.,
Для выполнения дискретного преобразования Уолша над комп;лексной последовательностью
ci. . 0,1,.., (N-1) -необходимо выполнить примерно 2N8og N операций сложения.
Обозначим время выполнения операции сложения t,; , а время операции умножения действительных чисел Цщ Ctj, . Константа С для современных вычислительных устройств лежит в пределах ,1-10.
Выигрый Т, даваемый.предлагаемым устройством,составляет
Ъ-bc ogгN V(gOgгN)NA-aJ t
З -Ьсл е Г - - м Для вычислительных устройств с фиксированной арифметикой:, t x5t . В этом случае
-r-.ibNCoe-xN llN NEog- NvlON
Наиболее типичные значения N лежат в пределах 128-1024. Для таких значений N выигрыш Т в вычислительных затратах составляет примерно 34 раза.
Блок формирования- весовых коэффициентов 6 работает следующим образом (см.фиг.2). Сигнал генератора поступает на управляющие входы первого и второго коммутаторов 11 и 17 По этому сигналу из блока памяти 10 осуществляется последовательная выборка первым коммутатором 11 значений ядер Фурье Ф(n,k) для различных значений k и фиксированного значения п, равного номеру генерируемого равномерно распределенного числа. Эти значения Ф() возводят ся в квадрат квадратора 12 и суммируются сумматором 13. После завершения определения (Ф(п,К))для
всех п О , 1, 2 , . . .N-1, из получе: ной суммы извлекается квадратный корень нелинейным преобразователем 14. Результирующее значение поступает на первый вход умножителя 15. На второй вход умножителя 15 поступает выбранное вторым коммутатором 17 значениес {К) , чис.ленко равное корню квадратному из требуемого значения энергетического спектра последовательности гауссовых случайных чисел. Полученные весовые коэффициенты накапливаются в блоке памяти 16.
Накопленные в блоке памяти 4 значения случайных равномерно
распределенных чисел, умноженных на весовые коэффициенты, подвергаются быстрому преобразованию Уолша в блоке 5. На выходе этого блока образуется последовательность гауссовых
0 случайных чисел с заданным энергетическим спектром. .
При практическом использовании предлагаемого устройства для генерации большого числа последовательностей из N гауссовых чисел с заданным энергетическим спектром, формирование весовых коэффициентов необходимо, выполнить только один раз, после чего их выборку осуществляют
0 из блока памяти 16. Формирование весовых коэффициентов Осуществляется согласно выражению
, btKb(K) 1Ф(.м,к)| ,
где ) - отсчеты требуемого энергетического спектра последовательности гауссовых чисел и Ф(п,К) п значения функции ядер Фурье (ciCK) ) и Ф(п,К) считаются заданными.
Для наиболее тийичных последовательностей длительностью 128-1024 чисел выигрнщ в вычислительных зае тратах предлагаемым устройством по сравнению с прототипом составит 3-4 раза.
Таким образом, основным преимуществом заявляемого устройства является уменьшение вычислительных затрат при генерации гауссовских v случайных чисел с заданным энергетическим спектром из равномерно распределенных.
Все блоки, входящие в предлагаемое 5 устройство, хорошо известны. Их реализация не вызывает затруднений. Предлагаемое устройство найдет применение в цифровых системах моделирования динамических объектов. Экономический эффект от применения предлагаемого устройства составит порядка 20-30 тыс.руб в год. Формула изобретения 1. Генератор случайных чисел, 5 содержащий генератор тактовых импульсов, первый выход которого соединен с входом генератора равномерн распределенных случайных чисел, -выход которого соединен с первым входом блока умножения, второй вход которого подключен к вызсоду ключа, выход блока умножения соединен с входом первого блока памяти, второй блок памяти, отличающийс я тем, что, с целью повышення быстродействия, он содержит блок формирования весовых коэффициентов блок быстрого преобразования Уолша и элемент задержки, вход которого подключен к второму выходу генератора тактовых импульсов, третий выход которого соединен с входом блка- формирования весовых коэффициентов, группа входов которого соединена с гpsшпoй выходов второго блок памяти соответственно, выход блока формирования весовых коэффициентов соединен с информационным входом ключа, управляющий вход которого подключен к выходу элемента задержки, выход первого блока памяти соединен с входом блока быстрого преобразования Уолша, выход которого является входом генератора.
формирования весовых коэффициентов содержит два блока памяти, два коммутатора, квадратор, сумматор, нели- J нейный преобразователь и умножитель, группа выходов первого блока памяти соединена с группой входов первого коммутатора соответственно, вход которого объединен с входо второго KOMMyTaiTopa и является входом блока, группой входов которого является
0 группа входов второго коммутатора, ;выход которого соединен с первым входом умножителя, выход.которого соединен с входом второго блока памяти, выход которого является выходом блока, выход первого коммутатора через последовательно соединенные квадратор, с5 -1матор и нелинейный преобразователь соединен с вторым входом умножителя.
0
Источники информации, принятые во внимание при экспертизе
5 1968.
0 т.12 5, 1972 (прототип).
От второго fuxoda токтокпо itffpamopa
От nepSoiB S/ioKa ptiucmpoB панлти
Авторы
Даты
1982-12-15—Публикация
1981-05-11—Подача