Изобретение относится к средствам механизации графических работ, в частности к чертежным приборам для вычерчивания лемнискат Жероно.
Известен механизм для воспроизведения лемнискаты Жероно, содержащий установленную на основании неподвижную направляющую с ползуном, несущим траверсу и шатун, связанный с траверсой посредством крестообразного- ползуна с взаимно перпендикулярными направляющими, несущего пишущий штифт }.
Недостатками известного механизма являются сложность настройки и то, что с его помощью можно воспроизводить только лемнискату Жероно.
Цель изобретения - расширение диапазона решаемых задач путем обеспечения вычерчивания различных кривых и упрощение настройки.
Поставленная цель достигается тем, что механизм для воспроизведения лемнискат Жероно, содержащий установленную на основании неподвижную направляющую с ползуном, несущим траверсу, и шатун, связанный с траверсой посредством крестообразного ползуна с взаимно перпен;1икулярными
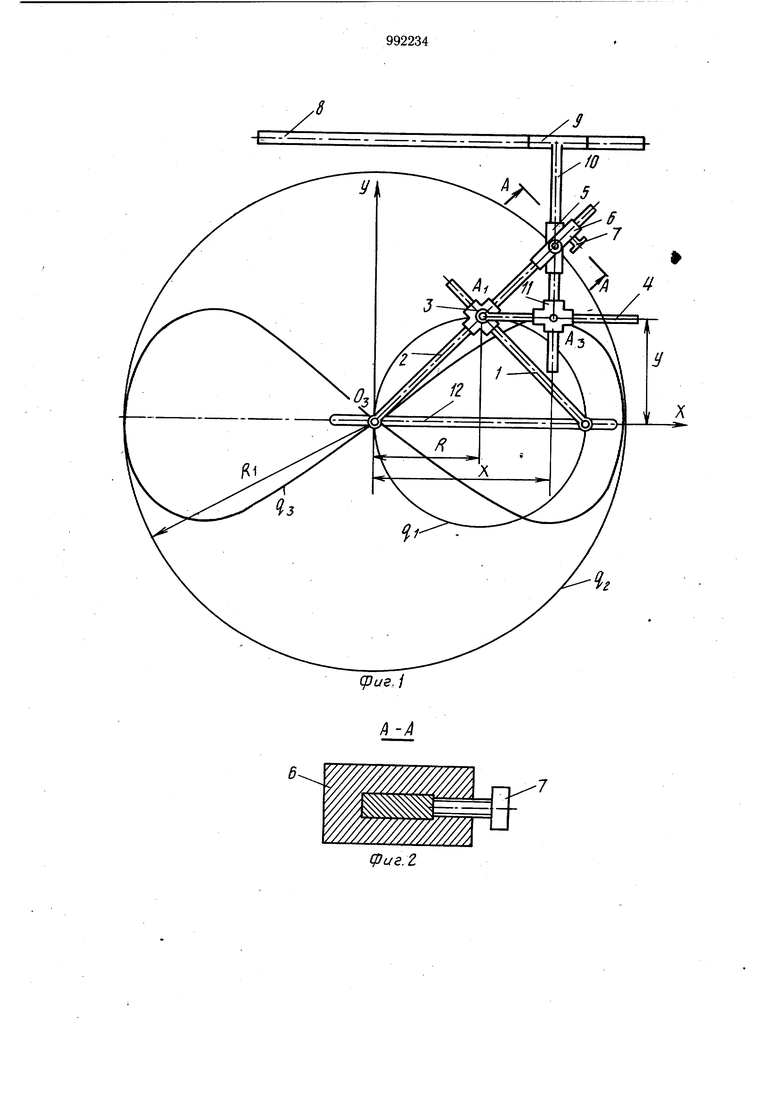
направляющими, несущего пишущий штифт, имеет две кулисы, установленные на основании посредством переставных шарниров и связанные между собой вторым крестообразным ползуном с взаимно перпендику5 лярными направляющими, и два шарнирно соединенных ползуна, один нз которых установлен на одной из кулис и имеет сгопрр,ный винт, а другой установлен на траверсе. На фиг. 1 изображен предлагаемый ме,0 ханизм; на фиг. 2 - разрез А-А на фиг. 1 (крепление ползуна на кулисе); на фиг. 3 - схема преобразования окружности на основе дву-двузначного соответствия в семействр кривых лемнискаты Жероно; на фиг. 4 - кинематическая схема механизма для вос15 произведения лемнискаты Жероно; на фиг. 5то же, для воспроизведения лемнискаты Слюза; на фиг. 6 и 7 - для воспроизведения кривой 2-го порядка - параболы.
Механизм содержит кулисы 1 и 2, установленные на основании посредством переставных шарниров О и Oj, подвижно связанных крестообразным ползуном 3, оси направляющих которого взаимно перпендикулярны. Крестообразный ползун 3 в точке А, образует вращательную пару с шатуном 4. Кулиса 2 и шатун 4 соединены между собой при помощи шарнирно связанных ползунов 5 и 6, при этом ползун 6 имеет стопорный винт 7. На основании установлена неподвижная направляющая 8 с ползуном 9, несущим траверсу 10, которая связана с шатуном 4 крестообразным ползуном 11. Переставные щарниры О и Oj установлены в прорези 12 основания.
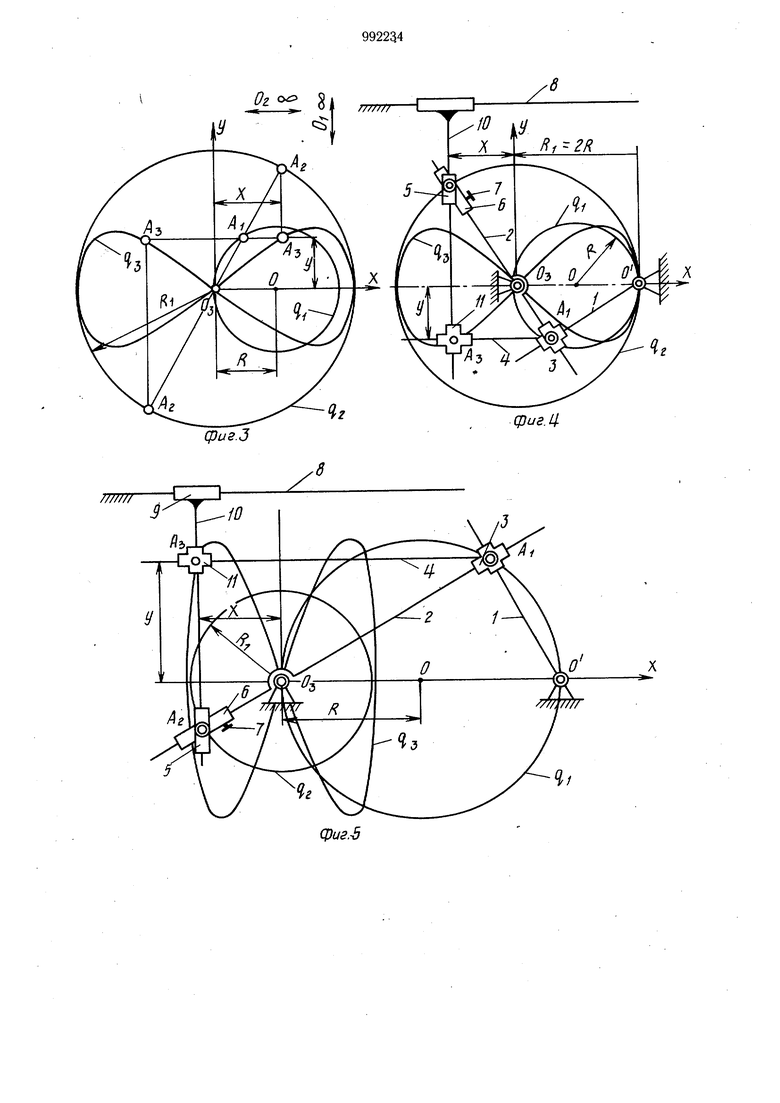
Геометрической основой механизма является преобразование Маклорена. На фиг. 3 показано преобразование окружности q, в кривую qj. Здесь ось преобразования имеет уравнение RI. а преобразуемая окружность - (x-fR) +Y R Центры преобразования Oi и О являются соответственно несобственными точками осей Озх и ОЗУ. где Оз - собственная точка и находится в начале прямоугольной координатной системы. Уравнение преобразуемой кривой Qj относящейся к семейству лемнискат Жероно относительно прямоугольной системы координат xOjY имеет вид
(1)
-
(4R2x2-R2Y2),
4R2
где R и RI - параметры аппарата преобразования. Придавая различные значения параметрам, можно получить семейства кривых разного порядка и формы.
Материализация модели аппарата преобразования приводит к организации 8-звенного механизма для воспроизведения кривых, описываемых уравнением (1) (фиг. 1).
Механизм работает следующим образом.
При вращении кулисы 1 вокруг оси О, вращается и кулиса 2 вокруг оси Оз, перемещая ползун 5 вдоль траверсы 10 ползуна 9. При этом крестообразный ползун 11 перемещается одновременно по траверсе 10 ползуна 9 и шатуну 4, а пишущий штифт, вставленный в АЗ, опищет кривую q. Настройка механизма для воспроизведения данной кривой осуществляется следующим образом.
Пусть заданы R и R|. В прорези 12 основания закрепляют шарниры О и Оз кулис 1 и 2 так, чтобы выдержалось условие OOj 2R. Переставной ползун 6 на кулисе 2 перемещают и жестко закрепляют винтом 7 с соблюдением условия . Механизм готов в работе.
Форма кривой зависит от параметров преобразования и взаимного расположения геометрических элементов аппарата преобразования. Поэтому механизм в зависимости от настройки воспроизводит семейства различных кривых.
Если в (1) R -, то получают общеизвестное уравнение лемнискаты Жероно
х Rf(x2- у2)
(2)
Кинематическая схема механизма для ее воспроизведения приведена на фиг. 4.
Если в (1) принять RI а, R п, где Ь - произвольная постоянная, то получают общеизвестное уравнение лемнискаты Слюза
Ь2у (а2 - х2) х2(3)
На фиг. 5 изображена кинематическая
схема механизма для ее воспроизведения.
При RI R из (1) получают кривую
4(R2 - Х2)х2,(4)
воспроизводимую тем же механизмом (фиг. 5).
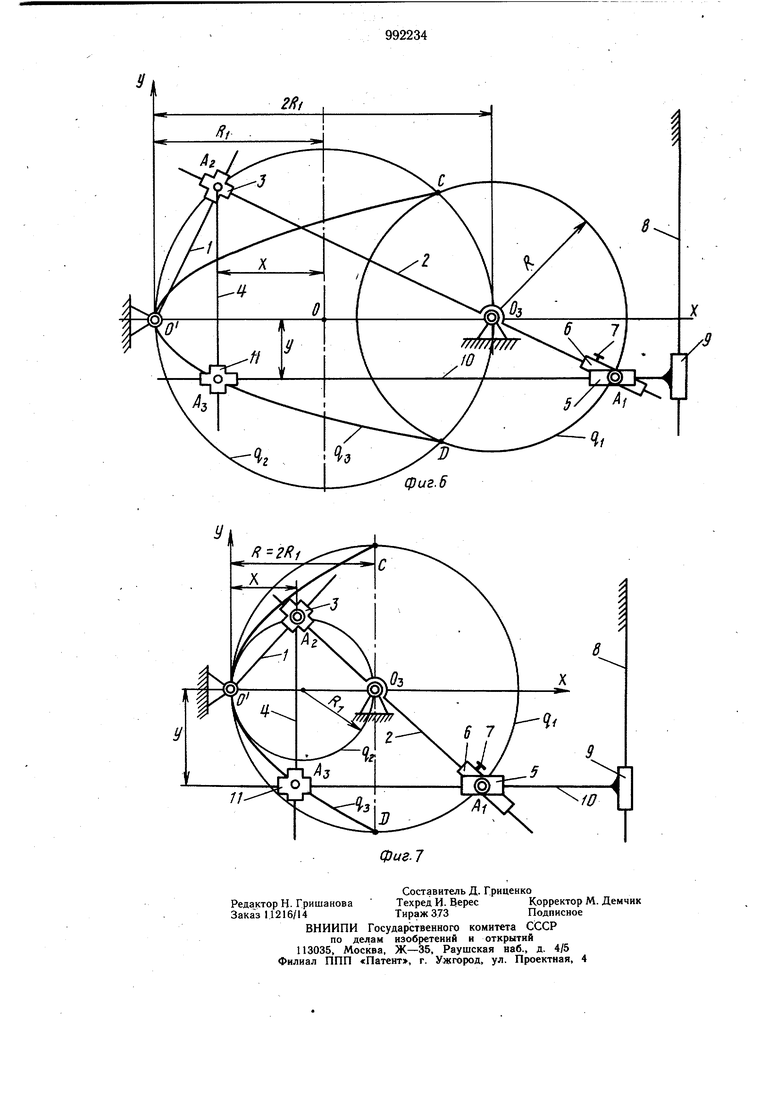
Если выдержать условие ООз 2R|, а ОзА) R (фиг. 1), то механизм будет воспроизводить параболу с уравнением
(5) 2R,
Rj R принимает вид
(6) 2
20 В случае, когда ООз 2Rj R механизм будет воспроизводить параболу с уравнением
2Rix
(7)
Кинематические схемы этих механизмов показаны соответственно на фиг. 6 и 7. Необходимо отметить, что механизм воспроизводит параболу по хорде CD, оси ООзи вершине о , что очень важно в инженерной
практике. Механизм имеет одну степень подвижности.
Применение предлагаемого механизма позволяет расширить диапазон вычерчиваемых кривых, упростить настройку и тем самым повысить производительность труда
при выполнении графических работ.
Формула изобретения
Механизм для воспроизведения лемнискаты Жероно, содержащий установленную на основании неподвижную направляющую с ползуном, несущим траверсу, и щатун, связанный с траверсой посредством крестообразного ползуна с взаимно перпендикулярными направляющими , несущего пишущий штифт, отличающийся тем, что, с целью расщирения диапазона решаемых задач, он имеет две кулисы, -установленные на основании посредством переставных шарниров и связанные между собой вторым крестообразным ползуном с взаимно перпендикулярными направляющими, и два шарнирно соединенных ползуна, один из которых установлен на одной из кулис и имеет стопорный винт, а другой установлен на траверсе.
Источники информации, принятые во внимание при экспертизе
1. Артоболевский И. И. Механизм в современной технике. Т. II, М., «Наука, 1971, с. 201.
,8
s
X

| название | год | авторы | номер документа |
|---|---|---|---|
| Механизм для воспроизведения виртуальной параболы Крамера | 1983 |
|
SU1094758A1 |
| Кулисно-рычажный механизм Мамырина для воспроизведения лемнискаты Жероно | 1986 |
|
SU1391967A1 |
| Кулисно-рычажный механизм Мамырина А.В. для воспроизведения кривых | 1987 |
|
SU1475834A1 |
| Механизм для преобразования окружности в кривые 3-го и 4-го порядка | 1980 |
|
SU901067A1 |
| Прибор для вычерчивания кривых | 1990 |
|
SU1729815A1 |
| Прибор для вычерчивания кривых | 1990 |
|
SU1729814A1 |
| Кулисно-рычажный механизм Мамырина А.В. для воспроизведения лемнискаты Жероно | 1983 |
|
SU1150097A1 |
| Шарнирно-рычажный механизм для воспроизведения кривых | 1983 |
|
SU1113284A1 |
| Прибор для вычерчивания кривых | 1986 |
|
SU1362669A1 |
| Кулисно-рычажный механизм преобразования кривых | 1987 |
|
SU1482824A1 |


Авторы
Даты
1983-01-30—Публикация
1981-09-11—Подача