Изобретение относится к вычислительной технике и может быть использовано в процессорах обработки сигналов, в цифровых фильтрах и т. п.
Цель изобретения - повышение отказоустойчивости устройства для вычисления сумм парных произведений.
Сущность изобретения заключается в следующем.
Основным достоинством системы остаточных классов (СОК) является независимость образования разрядов числа, в силу чего каждый разряд несет информацию обо всем исходном числе. Отсюда вытекает возможность их переллельной обработки. Это позволяет привлечь новые методы арифметического контроля. При введении дополнительного контрольного основания остаток, взятый по этому основанию, несет избыточную информацию об исходном числе, что позволяет обнаружить и исправить ошибки в цифрах по рабочим основаниям.
Любое число N, представленное в СОК как N= (α1α2. . . αn, αn+1), может быть выражено как
N = 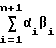 -rPn, (1) где βi - ортогональные базисы;
-rPn, (1) где βi - ортогональные базисы;
r - ранг числа;
Pn=  pi - полный диапазон (2);
pi - полный диапазон (2);
pi - основания СОК, i= 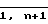 ;
;
n - число рабочих оснований;
Pn+1 - контрольное основание.
В то же время
Pn= 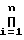 pi·pn+1= Р·pn+1, (3) где Р - рабочий диапазон.
pi·pn+1= Р·pn+1, (3) где Р - рабочий диапазон.
Число N считается правильным, если N<Р. Другими словами
S =  = 0, (4) где S - номер интервала, в котором находится число N.
= 0, (4) где S - номер интервала, в котором находится число N.
Подставим в равенство (4) равенство (1), тогда
S = 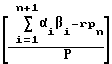 =
= 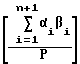 - rpn+1=
- rpn+1= 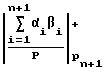 . (5)
. (5)
Известно, что βi= РRi+ Ai, где Ri= 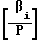 ; Ai - остаток от деления.
; Ai - остаток от деления.
Но Ai= βiI, где βiI - ортогональный базис с основанием p1, p2 . . . pn.
Полученные равенства подставляем в формулу (5), тогда
S = 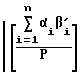 +
+ 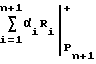
Но 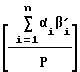 = r′ - ранг числа в системе по рабочим основаниям P1, P2, . . . Pn.
= r′ - ранг числа в системе по рабочим основаниям P1, P2, . . . Pn.
Так как выбранная система является упорядоченной (P1<P2 . . . <Pn<Pn+1) и величина Pn+1>2Pn Pn-1, то по величине S можно однозначно определить величину Δ коррекции результата. Например, пусть имеем систему оснований P1= 3, Р2= 5, Р3= 31. (контрольные основание Р3).
Тогда Pn= 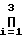 pi= 3·5·31= 465;
pi= 3·5·31= 465;
Р= p1·p2= 3·5= 15.
Вычислим ортогональные базисы
β 1= 310; β2= 186; β 3= 435.
Вычислим коэффициенты
β1= 15·R1+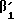 = 15·20+10;
= 15·20+10;
β2= 15·R2+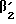 = 15·12+6;
= 15·12+6;
β3= 15·R3= 15·29.
Получаем
R1= 20, R2= 12, R3= 29, β1I= 10, β2I= 6
Возьмем N= 8. В СОК оно имеет вид N= (2, 3, 8).
Вычислим значение
S =  +20·2+12·3+29·8
+20·2+12·3+29·8 = 0.
= 0.
Допустим, что произошла ошибка и получено число N I= (1, 3, 8).
Тогда
S = 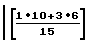 +20·1+12·3+29·8
+20·1+12·3+29·8 = 10.
= 10.
В соответствии со значением S, поданным на вход памяти, на выходе памяти появляется число, которое необходимо сложить с  :
:
Nист= 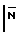 +
+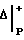 .
.
В нашем примере, память работает в соответствии с таблицей.
В соответствии с таблицей в первом примере имеем
N= 8, Nист= 8+0= 8,
во втором примере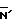 = 13, Nист=
= 13, Nист=  13+10
13+10 = 8.
= 8.
Ошибка исправлена.
На фиг. 1 представлена функциональная схема устройства для вычисления сумм парных произведений; на фиг. 2 - функциональная схема блока коррекции ошибки.
Устройство для вычисления сумм парных произведений (фиг. 1) содержит блоки вычисления парных произведений по произвольному модулю 1, 2 и по контрольному модулю 3, каждый из которых содержит регистр 4, память 5, матричный сумматор 6, матричный умножитель 7 и три группы буферных регистров 8, 9, 10, преобразователь 11 кода СОК в позиционный код, блок 12 коррекции ошибки, модульный сумматор 13, счетчик 14 тактов и выход 15 результата устройства.
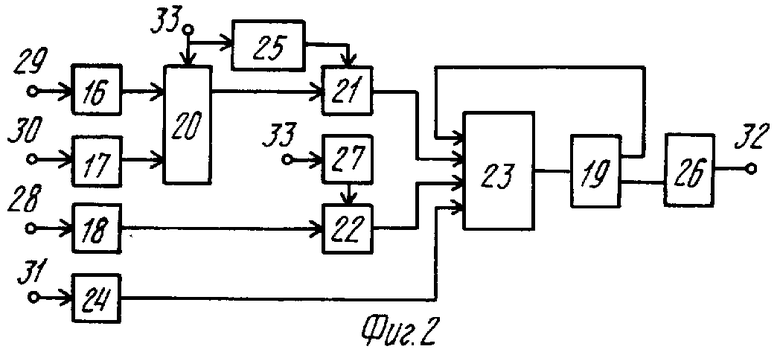
Блок 12 коррекции ошибки (фиг. 2) содержит четыре регистра 16-19, коммутатор 20, два матричных умножителя 21, 22, модульный сумматор 23, счетчик 24 тактов переходов, три памяти 25, 26, 27, информационные входы 28, 29, 30, 31 блока, выход 32 блока и вход 33 разрешения работы блока.
Памяти, матричные умножители, матричные сумматоры в устройстве выполнены в виде постоянных запоминающих устройств (ПЗУ).
Устройство работает следующим образом.
В информационные регистры 4 блоков 1, 2, 3 до начала работы записаны числа в коде СОК. Счетчик тактов формирует адреса для считывания коэффициентов, которые хранятся в блоках 1, 2, 3 в памяти 5 в коде СОК. Содержимое регистров 4 в каждом из блоков 1, 2, 3 перемножается с коэффициентами с помощью матричных умножителей 7. Результат умножения записывается в первую группу буферных регистров 8, содержимое которых складывается с содержимым буферных регистров 10 третьей группы (в первом цикле происходит сложение с нулем). Сложение осуществляют матричные сумматоры 6 в каждом из блоков 1, 2, 3. Сумма записывается в буферные регистры 10 третьей группы. С выходов буферных регистров 10 блоков 1 и 2 результат подается на входы преобразователя 11 кода СОК в позиционный код и на информационные входы блока 12 коррекции ошибки, на третий вход которого подается также информация с выходов буферных регистров 10 блока 3. Счетчик тактов по окончании суммирования парных произведений выдает разрешающий сигнал на вход разрешения преобразователя 11 и блока 12 коррекции ошибки. С второго выхода преобразователя 11 на четвертый вход блока 12 коррекции ошибки поступает сигнал о переходе через Р. Структура преобразователя 11 аналогична прототипу. Результаты с выходов преобразователя 11 кода СОК в позиционный код и блока 12 коррекции ошибки подаются на входы модульного сумматора 13, где и происходит сложение. Выход модульного сумматора 13 является выходом 15 устройств. Слагаемые кода СОК в информационные регистры 4 блоков 1, 2, 3 могут быть записаны из аналого-цифрового преобразователя.
Блок 12 коррекции ошибки работает следующим образом.
Значения α1, α2иα3 записываются в соответствующие регистры 16, 17, 18. Значения α1иα2 последовательно через коммутатор 20 подаются на умножитель 21, на второй которого поступает величина R1 и R2 с выхода памяти 25 ПЗУ. Значение α3 с выхода регистра 18 поступает на матричный умножитель 22, где производится умножение α3˙R3. Значения α1˙R1иα3˙R3подаются на вход модульного сумматора 23, где складываются. Результат заносится в регистр 19. Затем этот результат, который является промежуточным, поступает на вход сумматора 23, где суммируется со значением α2˙R2 . Полученный результат заносится в регистр 19, а затем снова подается на вход сумматора для сложения со значением rI , которое подается с выхода счетчика 24 числа переходов. Конечный результат поступает на вход памяти 26, на выходе которой появляется значение коррекции, которое подается на выход 32 блока коррекции ошибки.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления сумм парных произведений | 2019 |
|
RU2711731C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| СИСТОЛИЧЕСКИЙ ПРОЦЕССОР ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ С КОРРЕКЦИЕЙ ОШИБКИ | 1992 |
|
RU2018950C1 |
| СИСТОЛИЧЕСКИЙ ОТКАЗОУСТОЙЧИВЫЙ ПРОЦЕССОР ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ | 1992 |
|
RU2029437C1 |
| Устройство коррекции ошибок в модулярном коде на основе расширения системы оснований | 2017 |
|
RU2652446C1 |
| Устройство для вычисления сумм парных произведений | 1986 |
|
SU1310814A1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С ПЕРЕСЧЕТОМ ОРТОГОНАЛЬНЫХ БАЗИСОВ | 2005 |
|
RU2298873C1 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2013 |
|
RU2513915C1 |
Устройство для выполнения сумм парных произведений относится к вычислительной технике и может быть использовано в процессорах обработки сигналов, в цифровых фильтрах. Цель изобретения - повышение отказоустойчивости устройства, которая достигается введением блока 12 коррекции ошибки, модульного сумматора 13, блока 3 вычисления сумм парных произведений по контрольному основанию, которые в совокупности обеспечивают обнаружение и исправление одиночных ошибок по рабочим основаниям. 1 з. п. ф-лы, 1 табл. , 2 ил.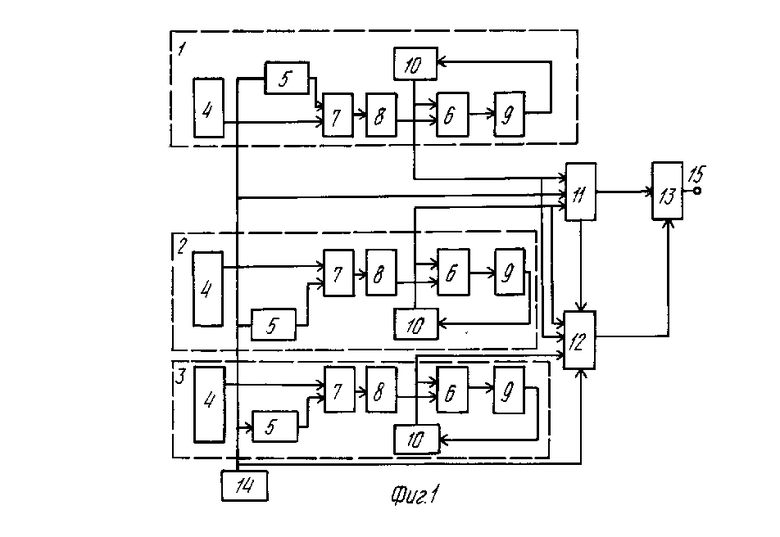
Авторы
Даты
1994-04-30—Публикация
1992-06-08—Подача