Изобретение относится к вычислительной технике, в частности к модулярным спецпроцессорам (СП), функционирующим в полиномиальной системе классов вычетов (ПСКВ) и способным сохранить работоспособное состояние при возникновении ошибки за счет реконфигурации структуры.
Известно устройство для преобразования из полиномиальной системы классов вычетов в позиционный код (Патент №2409840, G06F 11/07, опубликовано 20.01.2011, бюл. №2), которое содержит вход запуска устройства, группу сдвиговых регистров, блок синхронизации, выход устройства, группу блоков расчета ортогональных базисов, блоки трехвходовых элементов И, сумматор по модулю два, группу информационных входов, группу управляющих входов, при этом группа блоков расчета ортогональных базисов содержит первый блок памяти, умножитель, второй блок памяти, второй умножитель, регистр, выход регистра.
Недостатком данного устройства является низкая скорость преобразования из кода ПСКВ в позиционный код.
Техническим результатом изобретения является повышение скорости преобразования из кода ПСКВ в позиционный код за счет снижения времени вычисления ортогональных базисов модулярного кода
Указанный технический результат достигается за счет ввода в конструкцию блока расчета ортогональных базисов сумматора по модулю и преобразователя «индекс - элемент» вместо первого умножителя по модулю pi(z), используемого в прототипе.
Предлагается устройство для преобразования из полиномиальной системы классов вычетов в позиционный код, содержащее вход запуска устройства, группу сдвиговых регистров, блок синхронизации, выход устройства, блоки элементов И, группу информационных входов, причем вход запуска устройства соединен с входом запуска блока синхронизации, выход которого соединен с входами разрешения сдвига сдвиговых регистров группы, информационные входы которых являются соответствующими информационными входами группы устройства, выход i-го сдвигового регистра группы соединен с первым входом элемента И i-й группы (i=1, 2, …, n), причем устройство содержит группу блоков расчета ортогональных базисов, сумматор по модулю два, управляющие входы устройства, причем выходы блока синхронизации подключены к первому входу блоков расчета ортогональных базисов, второй вход которых подключен к управляющим входам устройства, выход i-го блока расчета ортогональных базисов подключен ко второму входу элементов И i-го блока, третьи входы которых соединены с соответствующим управляющим входом группы, выходы элементов И соединены со входами сумматора по модулю два, выход которого является выходом устройства. При этом согласно изобретению блок расчета ортогональных базисов содержит синхровходы, n управляющих входов, первый и второй блоки памяти, умножитель, сумматор по модулю, регистр, преобразователь индекс-элемент, причем синхровходы подключены к первому и второму блокам памяти и регистру, n управляющих входов, подключенных к первому и второму блокам памяти, выход первого блока памяти подключен к первому входу сумматора по модулю, выход второго блока памяти подключен к второму входу умножителя, выход сумматора по модулю подключен ко входу регистра, первый выход регистра подсоединен ко входу преобразователя индекс-элемент, выход преобразователя индекс-элемент подключен к первому входу умножителя, ко второму входу умножителя подсоединен выход второго блока памяти, второй выход регистра подключен ко второму входу сумматора по модулю, выход умножителя является выходом блока.
Для перевода из кода ПСКВ в позиционный код используется китайская теорема об остатках (КТО), согласно которой
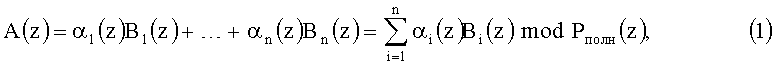
где Bi(z) - ортогональный базис i-го основания,
Ортогональный базис определяется как

где mi(z) - вес ортогонального базиса i-го основания.
Применение mi(z) позволяет обеспечить выполнение условия
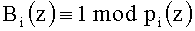 .
.
Преобразуем выражение (2) к виду

Подставив равенство (3) в выражение (1), получаем

где 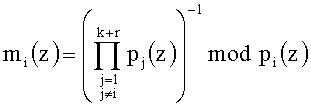 - обратная величина основания pj(z) по модулю pi(z); k - количество информационных оснований; r - количество контрольных оснований; k+r=n.
- обратная величина основания pj(z) по модулю pi(z); k - количество информационных оснований; r - количество контрольных оснований; k+r=n.
С целью повышения скорости вычисления ортогонального базиса Bi(z) предполагается отказаться от выполнения мультипликативной процедуры (4) вычисления веса mi(z) и перейти к использованию индексного представления, которое позволяет свести вычисление mi(z) в виде совокупности аддитивных операций.
Для эффективной реализации операций мультипликативного типа (умножение, деление, возведение в степень) характерно использование теории индексов. Число iA, являющееся решением сравнения

называется индексом числа А и обозначается iA=indA. Первообразный корень g называется основанием индекса.
Известно, что индекс J произведения простых целых чисел A1, А2, …, Ak по модулю p равен сумме индексов сомножителей, взятой по модулю р-1, т.е.

где i1, i2, …, ik - индексы положительных чисел A1, А2, …, Ak по модулю p при первообразном коде g.
Таким образом, очевидна возможность сведения операции умножения двух операндов А и В по модулю р к операции суммирования индексов iA, iB этих операндов при первообразном корне g по модулю р-1.
Структура устройства показана на фиг.1. Устройство содержит вход 1 запуска устройства, группу сдвиговых регистров 2, блок 3 синхронизации, выход 4 устройства, группу блоков 5 расчета ортогональных базисов, блоки 6 трехвходовых элементов И, сумматор 7 по модулю два, группу информационных входов 8, группу управляющих входов 9 устройства.
Вход 1 запуска устройства соединен с входом запуска блока 3 синхронизации, выход которого соединен с входами разрешения сдвига сдвиговых регистров группы 2, информационные входы которых являются соответствующими информационными входами 8 группы устройства, выход i-го сдвигового регистра группы 2 соединен с первым входом элемента И i-ой группы (i=1, 2, …, n) блоков 6 трехвходовых элементов И. Выходы блока 3 синхронизации также подключены к первому входу блоков 5 расчета ортогональных базисов, второй вход которых подключен к управляющим входам устройства 9, выход i-го блока расчета ортогональных базисов 5 подключен ко второму входу элементов И i-го блока 6, третьи входы которых соединены с соответствующим управляющим входом группы 9, выходы элементов И блока 6 соединены со входами сумматора 7 по модулю два, выход которого является выходом устройства 4.
С целью повышения скорости вычисления ортогонального базиса в блоках 5 расчета ортогональных базисов вместо умножителя по модулю pi(z), (где i=1, 2, … n), используемого в прототипе, устанавливаем сумматор по модулю 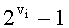 , где
, где 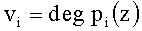 и преобразователь индекс-элемент.
и преобразователь индекс-элемент.
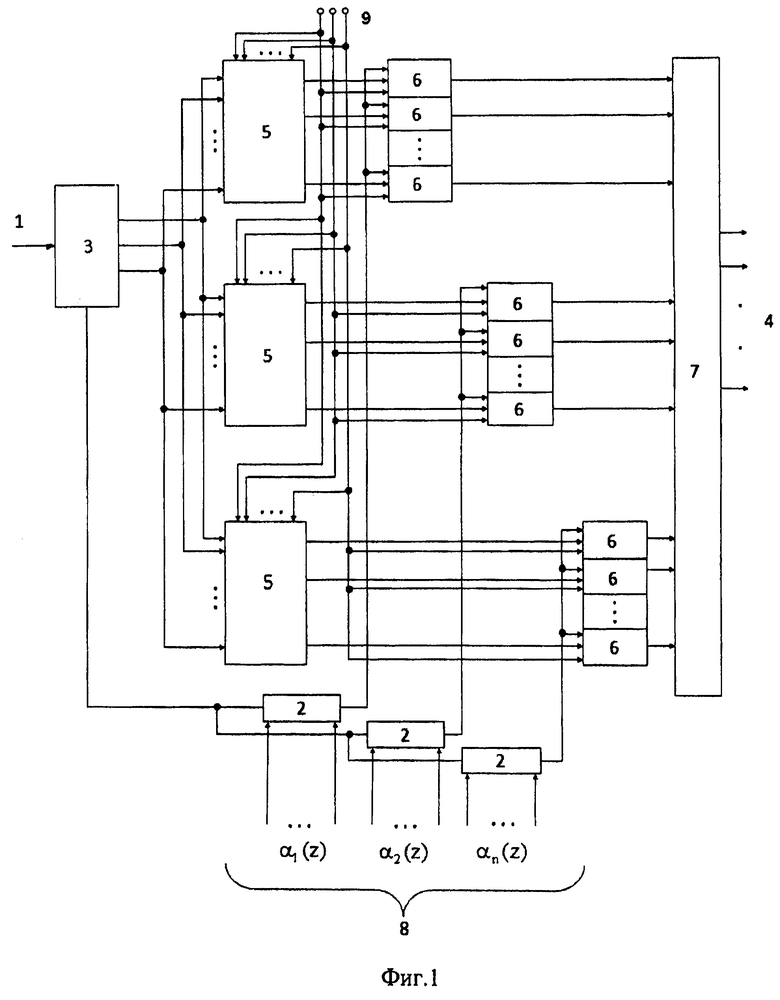
Блок расчета ортогональных базисов содержит синхровходы 10, n управляющих входов 11, первый блок памяти 12, сумматор по модулю 13, регистр 14, преобразователь индекс-элемент 15, второй блок памяти 16, умножитель 17, выход 18 блока. Структура блока показана на фиг.2.
Синхровходы 10 подключены к синхровходам первого блока памяти 12, второго блока памяти 16, регистра 14, а управляющие входы 11 подключены адресным входам первого 12 блока памяти и второго блока памяти 16. Первый вход сумматора по модулю 13 подключен к выходу первого блока памяти 12, а второй вход сумматора по модулю подсоединен ко второму входа регистра 14. Вход регистра 14 подключен к выходу сумматора по модулю 13. Вход преобразователя индекс-элемент 15 подключен к первому выходу регистра 14, а выход подсоединен к первому входу умножителя 17, второй вход которого подключен к выходу второго блока памяти 16. Выход умножителя 17 является выходом 18 блока расчета ортогональных базисов.
Число, представляемое в коде ПСКВ, A(z)=(α1(z), α2(z), …, αn(z)), через группу информационных входов 8 заносится на сдвиговые регистры 2 группы, причем вычеты по каждому из оснований ПСКВ заносятся в свой регистр 2. Работа устройства происходит по тактам. В каждом такте содержимое регистров 2 сдвигается вправо (в сторону младших разрядов) на один разряд. Алгоритм работы устройства может быть представлен в виде

где n - количество оснований ПСКВ;
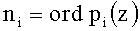 - степень i-го основания ПСКВ;
- степень i-го основания ПСКВ;
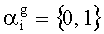 - значение g-го разряда, i-го основания ПСКВ;
- значение g-го разряда, i-го основания ПСКВ;
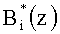 - пересчитанное значение i-го ортогонального базиса.
- пересчитанное значение i-го ортогонального базиса.
Из выражения (7) видно, что устройство реализует операцию последовательного суммирования произведений пересчитанных ортогональных базисов 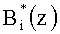 назначения остатка αi(z), представленного в двоичном коде.
назначения остатка αi(z), представленного в двоичном коде.
Блок расчета ортогональных базисов 5 работает следующим образом. При поступлении первого синхросигнала от блока синхронизации 3 на входы 10 из первого блока памяти 12 на первый вход сумматора по модулю 13 подается первое значение индекса 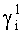 , которое суммируется с нулем и подается на вход регистра 14. При приходе второго синхросигнала на входы 10 полученный результат со второго выхода регистра 14 подается на второй вход сумматора по модулю 13, на первый вход которого поступает второе значение индекса
, которое суммируется с нулем и подается на вход регистра 14. При приходе второго синхросигнала на входы 10 полученный результат со второго выхода регистра 14 подается на второй вход сумматора по модулю 13, на первый вход которого поступает второе значение индекса 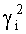 с выхода первого блока памяти 12.
с выхода первого блока памяти 12.
Спустя n-1 такт в регистре 14 находится значение индекса веса ортогонального базиса mi(z), согласно

Причем величины 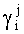 определяются значением сигнала, поступающего c j-го управляющего входа 11, согласно условию
определяются значением сигнала, поступающего c j-го управляющего входа 11, согласно условию

Значения сигналов, поступающих по управляющим входам 11, определяются из условия
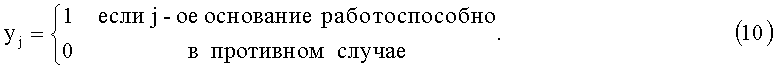
Вычисленное значение индекс γi веса ортогонального базиса поступает на вход преобразователя индекс-элемент 15. Он предназначен для преобразования двоичного кода индекса γi в двоичный код веса mi(z). Таким образом, данный преобразователь индекс-элемент 15 может быть реализован на основе кодопреобразователя.
Полученное значение mi(z) веса ортогонального базиса по i-му основанию подается на первый вход умножителя 17, а на второй вход последнего поступает с выхода второго блока памяти 16 значение

где l∉Uотк; Uотк - множество отказавших оснований в процессе функционирования вычислительной системы ПСКВ; g=0, 1, …, deg pi(z)-1.
Значение констант zgP*(z) хранится во втором блоке памяти 16 и выбирается согласно сигналам, поступающим по управляющим входам 11.
С выхода умножителя 17 снимается значение

которое поступает на выход 18 блока расчета ортогональных базисов.
Если в процессе функционирования вычислительной системы ПСКВ откажет b-е основание, то на управляющих входах 9 появится сигнал
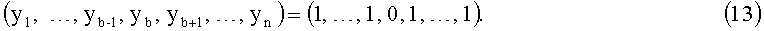
Данный сигнал поступает на управляющие входы 11 блоков 5 расчета ортогональных базисов. Под управлением данного сигнала из первого блока 12 памяти значения индексов 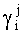 , а в сумматоре по модулю 13 за (n-2) такта вычисляется значение индекса γi согласно (8). При этом
, а в сумматоре по модулю 13 за (n-2) такта вычисляется значение индекса γi согласно (8). При этом 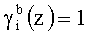 .
.
Под управлением сигналов, поступивших с управляющих входов 11, и синхровходов 10, из второго блока 16 памяти поступают значения, определенные выражением (11). Умножитель 17 реализует выражение (12), где

Одновременно с этим значения (y1, …, yb-1, yb, yb+1, …, yn)=(1, …, 1, 0, 1, …, 1) подаются на третьи входы 6 элементов И блоков 6. Нулевой сигнал yb=0 производит закрытие элементов И b-го блока 6. Таким образом, значения αb(z)·Bb(z) в получении конечного результата согласно не участвуют, так как на сумматор 7 они не подаются.
Рассмотрим пример
Необходимо вычислить значение ортогональных базисов ПСКВ с основаниями p1(z)=z+1, p2(z)=z2+z+1, p3(z)=z4+z3+z2+z+1, p4(z)=z4+z3+1, p5(z)=z4+z+1.
Согласно (14) и учитывая, что отказавших оснований нет, определяем значения Pi(z)
P1(z)=p2(z)p3(z)p4(z)p5(z)=z14+z13+z12+z11+z10+z9+z8+z7+z6+z5+z4+z3+z2+z+1;
P2(z)=p1(z)p3(z)p4(z)p5(z)=z13+z12+z10+z9+z7+z6+z4+z3+z+1;
Р3(z)=p1(z)p2(z)p4(z)p5(z)=z11+z10+z6+z5+z+1;
P4(z)=p1(z)p2(z)p3(z)p5(z)=z11+z10+z9+z8+z6+z4+z3+1;
P5(z)=p1(z)p2(z)p3(z)p4(z)=z11+z8+z7+z5+z3+z2+z+1;
Для выполнения условия 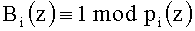 вычислим значения весов ортогональных базисов. Получаем m1(z)=1; m2(z)=z; m3(z)=z3+z; m4(z)=z3; m5(z)=z.
вычислим значения весов ортогональных базисов. Получаем m1(z)=1; m2(z)=z; m3(z)=z3+z; m4(z)=z3; m5(z)=z.
Определим значения m1(z). Тогда
m1(z)=1; m2(z)=z2(z+1)mod(z2+z+1)=z;
m3(z)=[(z3+z)(z3+1)(z2+1)(z3+z2+1)]mod(z4+z3+z2+z+1)=z3+z;
m4(z)=[z5(z3+z+1)(z3+z2+z+1)]mod(z4+z3+1)=z3;
m5(z)=[(z3+z2+z)(z3+z)(z2+z)(z3+z2)]mod(z4+z+1)=z.
Рассмотрим работу группы блоков расчета ортогональных базисов 5 на примере блока, функционирующего по модулю p5(z)=z4+z+1. Представим все основания ПСКВ в виде элементов поля, порождаемых модулем p5(z)=z4+z+1
Тогда имеем
p1(z)mod p5(z)=(z+1)mod(z4+z+1)=z+1
p2(z)mod p5(z)=(z2+z+1)mod(z4+z+1)=z2+z+1
p3(z)mod p5(z)=(z4+z3+z2+z+1)mod(z4+z+1)=z3+z2
p4(z)mod p5(z)=(z4+z3+1)mod(z4+z+1)=z3+z
В таблице 1 представлено соответствие значений оснований и используемых индексов
Таблица 1
Так как все каналы находятся в работоспособном состоянии, то на управляющих входах появится сигнал (y1, y2, y3, y4, y5)=(1, 1, 1, 1, 1), который поступает на управляющие входы 11 блока расчета ортогонального базиса 5 при поступлении первого сигнала.
При поступлении первого сигнала по входу 10 с выхода первого блока памяти 12 выдается значение 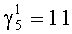 . Так, степень полинома р5(z) равна deg p5(z)=4, то сумматор 13 работает по модулю М=24-1=15. Поступившее значение
. Так, степень полинома р5(z) равна deg p5(z)=4, то сумматор 13 работает по модулю М=24-1=15. Поступившее значение 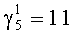 по первому входу сумматора 13 по модулю складывается с нулем. Полученный результат записывается в регистр 14.
по первому входу сумматора 13 по модулю складывается с нулем. Полученный результат записывается в регистр 14.
При поступлении второго сигнала по входу 10 с выхода первого блока памяти 12 на первый вход сумматора 13 по модулю выдается значение 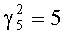 . Это значение складывается по модулю 15, с результатом
. Это значение складывается по модулю 15, с результатом 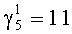 , поступившим по второму входу сумматора 13 из регистра 14. Результат операции
, поступившим по второму входу сумматора 13 из регистра 14. Результат операции
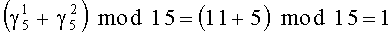
записывается в регистр 14.
При поступлении третьего сигнала по входу 10 с выхода первого блока памяти 12 на первый вход сумматора 13 по модулю выдается значение 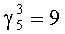 . Это значение складывается с предыдущим результатом, поступившим по второму входу сумматора 13 и с регистра 14. Результат операции (1+9) mod 15=10 записывается в регистр 14.
. Это значение складывается с предыдущим результатом, поступившим по второму входу сумматора 13 и с регистра 14. Результат операции (1+9) mod 15=10 записывается в регистр 14.
При поступлении четвертого сигнала по входу 10 с выхода первого блока памяти 12 на первый вход сумматора 13 по модулю выдается значении 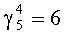 . Это значение складывается с предыдущим результатом, поступившим по второму входу сумматора 13 по модулю из регистра 4. В результате получаем значение индекса γ5=(10+6) mod 15=1 для веса m5(z) ортогонального базиса B5(z).
. Это значение складывается с предыдущим результатом, поступившим по второму входу сумматора 13 по модулю из регистра 4. В результате получаем значение индекса γ5=(10+6) mod 15=1 для веса m5(z) ортогонального базиса B5(z).
Полученное значение с первого выхода регистра 14 поступает на вход преобразователя индекс-элемент 15. Данный преобразователь преобразует входной код индекса в двоичный код элемента согласно таблице 2.
Тогда с выхода преобразователя индекс-элемент 15 снимается значение m5(z)=z=0010. Полученное значение с выхода преобразователя 15 подается на первый вход умножителя 17, на второй вход которого подается значение
P5(z)=p1(z)p2(z)р3(z)p4(z)=z11+z8+z7+z5+z3+z2+z+1
с выхода второго блока памяти 16. Данное значение определяется сигналом, поступающим по управляющим входам 11
(y1, y2, y3, y4, y5)=(1, 1, 1, 1, 1).
В результате значения ортогонального базиса будет равно
B5(z)=m5(z)P5(z)=zl2+z9+z8+z6+z4+z3+z2+z.
Остальные блоки 5 работают аналогично.
Проведем сравнительный анализ скорости вычисления ортогональных базисов в прототипе и предложенном устройстве.
В прототипе для вычисления веса ортогонального базиса требуется (n-1) умножений по модулю. При использовании комбинационного типа умножения это время составит
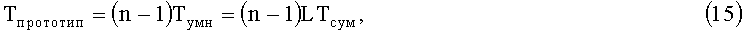
где Тумн - время выполнения операции умножения L-разрядных операндов;
Тсум - время выполнения операции сложения; L - разрядность умножителя.
В предложенном устройстве для вычисления веса ортогонального базиса требуется выполнение (n-1) сложения по модулю и преобразование «индекс-элемент». Последняя операция может быть реализована с использованием последовательного соединения кодера и декодера, тогда время вычисления веса ортогонального базиса будет определяться

где TCD - время срабатывания кодера; TDC - время срабатывания декодера.
Анализ выражений (15) и (16) показывает, что замена мультипликативной операции получения веса mi(z) аддитивной позволяет повысить скорость вычисления ортогонального базиса.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2409840C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С ПЕРЕСЧЕТОМ ОРТОГОНАЛЬНЫХ БАЗИСОВ | 2005 |
|
RU2298873C1 |
| Устройство коррекции ошибок в модулярном коде на основе расширения системы оснований | 2017 |
|
RU2652446C1 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЛА ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С КОРРЕКЦИЕЙ ОШИБКИ | 2006 |
|
RU2309535C1 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССА ВЫЧЕТОВ | 2004 |
|
RU2267808C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ С КОРРЕКЦИЕЙ ОШИБОК | 2015 |
|
RU2584495C1 |
Изобретение относится к вычислительной технике, в частности к модулярным спецпроцессорам, функционирующим в полиномиальной системе классов вычетов и способным сохранять работоспособное состояние при возникновении ошибки за счет реконфигурации структуры. Техническим результатом является повышение скорости преобразования. Устройство содержит вход запуска устройства, группу сдвиговых регистров, блок синхронизации, выход устройства, блоки трехвходовых элементов И, сумматор по модулю два, группу информационных входов, группу управляющих входов устройства, группу блоков расчета ортогональных базисов, каждый из которых содержит блоки памяти, сумматор по модулю, регистр, преобразователь индекс-элемент, умножитель. 2 ил., 2 табл.
Устройство для преобразования из полиномиальной системы классов вычетов в позиционный код, содержащее вход запуска устройства, группу сдвиговых регистров, блок синхронизации, выход устройства, блоки элементов И, группу информационных входов, причем вход запуска устройства соединен с входом запуска блока синхронизации, выход которого соединен с входами разрешения сдвига сдвиговых регистров группы, информационные входы которых являются соответствующими информационными входами группы устройства, выход i-го сдвигового регистра группы соединен с первым входом элемента И i-й группы (i=1, 2, …, n), причем устройство содержит группу блоков расчета ортогональных базисов, сумматор по модулю два, управляющие входы устройства, причем выходы блока синхронизации подключены к первому входу блоков расчета ортогональных базисов, второй вход которых подключен к управляющим входам устройства, выход i-го блока расчета ортогональных базисов подключены ко второму входу элементов И i-го блока, третьи входы которых соединены с соответствующим управляющим входом группы, выходы элементов И соединены со входами сумматора по модулю два, выход которого является выходом устройства, отличающееся тем, что блок расчета ортогональных базисов содержит синхровходы, n управляющих входов, первый и второй блоки памяти, умножитель, сумматор по модулю, регистр, преобразователь индекс-элемент, причем синхровходы подключены к первому и второму блока памяти и регистру, n управляющих входов, подключенных к первому и второму блокам памяти, выход первого блока памяти подключен к первому входу сумматора по модулю, выход второго блока памяти подключен к второму входу умножителя, выход сумматора по модулю подключен ко входу регистра, первый выход регистра подсоединен ко входу преобразователя индекс-элемент, выход преобразователя индекс-элемент подключен к первому входу умножителя, ко второму входу умножителя подсоединен выход второго блока памяти, второй выход регистра подключен ко второму входу сумматора по модулю, выход умножителя является выходом блока.
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2409840C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С ПЕРЕСЧЕТОМ ОРТОГОНАЛЬНЫХ БАЗИСОВ | 2005 |
|
RU2298873C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЛА ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С КОРРЕКЦИЕЙ ОШИБКИ | 2006 |
|
RU2309535C1 |
| Устройство для преобразования числа из системы остаточных классов в позиционный код | 1987 |
|
SU1501280A1 |
| US 2010030832 A1, 04.02.2010 | |||
| УСТРОЙСТВО для ЗАКРУТКИ ПРОВОЛОКИ | 0 |
|
SU312030A1 |
| US 2005089161 A1, 28.04.2005 | |||
| CN 101753147 A, 23.06.2010 | |||
Авторы
Даты
2014-04-20—Публикация
2013-01-09—Подача