Заявленное изобретение относится к вычислительной технике и, в частности к непозиционным компьютерным устройствам, и предназначено для обеспечения требуемой точности при вычислении с использованием модулярного кода.
Известно устройство расширения оснований модулярного кода [1] (Патент РФ №2562366, Устройство расширения оснований модулярного кода), которое имеет вход устройства, первый блок умножителей, который содержит n умножителей по модулю pi(z), где i=1, 2,…, n, первый блок памяти для хранения ортогональных весов mi(z); второй блок умножителей, который содержит n умножителей по модулю pn+1(z), второй блок памяти для хранения 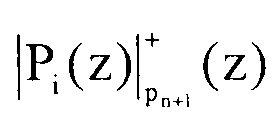 , сумматор по модулю два, выход устройства.
, сумматор по модулю два, выход устройства.
Недостатком устройства является невозможность выполнения процедуры исправления ошибок, возникающих в процессе работы вычислительного устройства, функционирующего в модулярных кодах.
Целью изобретения является расширение функциональных возможностей устройства, то есть проведения коррекции ошибок кодом полиномиальной системы классов вычетов (ПСКВ), на основе использования операций расширения оснований.
Техническим результатом, достигнутым при осуществлении заявленного изобретения, является расширение функциональных возможностей устройства, позволяющих исправлять ошибки в кодовой комбинации ПСКВ на основе выполнения операции расширения оснований.
Указанный технический результат достигается за счет введения блока регистров, состоящего из n+2 регистров, предназначенных для хранения остатков, где n - количество информационных оснований ПСКВ, n+1 и n+2 - контрольные основания ПСКВ, блока вычисления второго контрольного остатка, структура которого соответствует структуре прототипа [1], двух сумматоров вычисления синдрома ошибки, блока памяти, предназначенного для хранения вектора ошибки, n+2 корректирующих сумматоров, с помощью которых происходит исправление ошибки по модулю два.
Используя коды ПСКВ, можно операцию сложения, вычитания и умножения двух операндов, представленных в полиномиальной форме A(z) и B(z), свести к выполнению этих операций над соответствующими остатками αi(z) и βi(z). При этом в ПСКВ эти операции производятся независимо по каждому из модулей pi(z), что указывает на параллелизм данной алгебраической системы.
Кроме того, особенность ПСКВ состоит еще и в том, что независимость обработки информации по основаниям ПСКВ позволяет не только повысить скорость и точность обработки, но также и обеспечить обнаружение и коррекцию ошибок в процессе функционирования вычислительного устройства.
В ПСКВ в качестве оснований системы используются неприводимые полиномы pi(x), где i=1, 2, …, n, любой полином А(х), удовлетворяющий условию

где 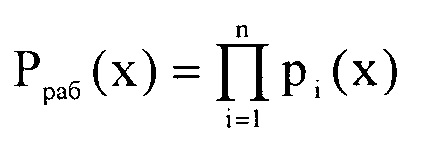 - рабочий диапазон системы, degPраб(x) - степень полинома, можно однозначно представить в виде набора остатков
- рабочий диапазон системы, degPраб(x) - степень полинома, можно однозначно представить в виде набора остатков
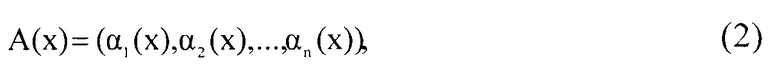
где αi(x)=А(x)modpi(x); i=1, 2, …, n.
Для обнаружения и исправления однократных ошибок в модулярном коде полинома А(x)=(α1(x),α2(x),…,αn(x)) вводят два контрольных основания pn+1(x) и pn+2(x), которые удовлетворяют условию
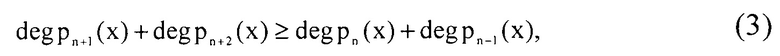
Наличие двух контрольных оснований позволяет определить местоположение ошибки и ее глубину в коде ПСКВ.
Возникновение ошибки в непозиционной кодовой конструкции A(z) переводит ее из подмножества разрешенных комбинаций в подмножество запрещенных. Согласно китайской теореме об остатках (КТО) значение ошибочного полинома A*(z) в этом случае определяется выражением

где  - полный диапазон кода ПСКВ; Δαj(z) - глубина ошибки по j-му основанию кода ПСКВ; Bj(z) - ортогональный базис j-го основания кода ПСКВ; j=1, 2, …, n+2.
- полный диапазон кода ПСКВ; Δαj(z) - глубина ошибки по j-му основанию кода ПСКВ; Bj(z) - ортогональный базис j-го основания кода ПСКВ; j=1, 2, …, n+2.
Анализ выражения (4) показывает, что местоположение ошибочного полинома A*(z) относительно рабочего диапазона Pраб(z) определяется величиной второго слагаемого.
Рассмотрим алгоритм перевода из безызбыточного полиномиального модулярного кода в позиционный код согласно КТО имеем
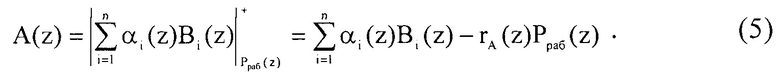
где Вi(z)=mi(z)Pi(z) - ортогональный базис; mi(z) - вес ортогонального базиса;  - ранг кода ПСКВ.
- ранг кода ПСКВ.
Воспользуемся определением ортогональных базисов, тогда выражение (5) можно представить в виде
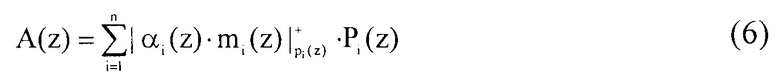
Умножение остатка αi(z) на вес ортогонального базиса mi(z) выполняется по модулю pi(z), что позволяют отказаться от вычисления ранга rA(z) при использовании китайской теоремы об остатках при переводе к позиционному коду.
Чтобы осуществить поиск и коррекцию ошибки в коде ПСКВ на основе расширения системы оснований, необходимо, используя остатки по рабочим основаниям (α1(z), …, αn(z)), вычислить остатки по контрольным основаниям pn+1(z) и pn+2(z).
Тогда для вычисления первого контрольного остатка 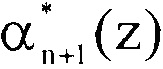 по основанию pn+1(z) используем следующее выражение
по основанию pn+1(z) используем следующее выражение
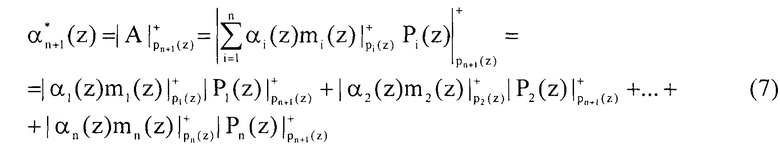
Вычисление второго контрольного остатка 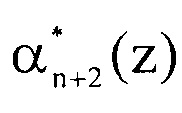 по основанию pn+2(z) определяется выражением
по основанию pn+2(z) определяется выражением
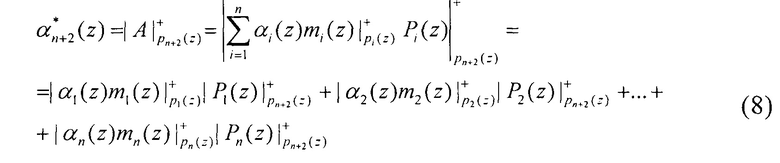
После этого вычисленные остатки  и
и  складываются по модулю два с остатками αn+1(z) и αn+2(z), которые входят в состав комбинации кода ПСКВ A(z)=(α1(z), α2(z), …, αn+1(z), αn+2(z)). В результате получается синдром ошибки, который определит местоположение и глубину ошибки в коде
складываются по модулю два с остатками αn+1(z) и αn+2(z), которые входят в состав комбинации кода ПСКВ A(z)=(α1(z), α2(z), …, αn+1(z), αn+2(z)). В результате получается синдром ошибки, который определит местоположение и глубину ошибки в коде
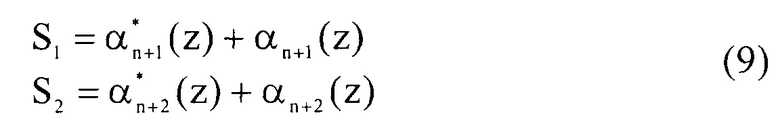
Если полученный синдром будет равен нулю, то это означает, что код ПСКВ не содержит ошибки. Если синдром будет отличен от нуля, то это будет означать, что код ПСКВ содержит ошибку.
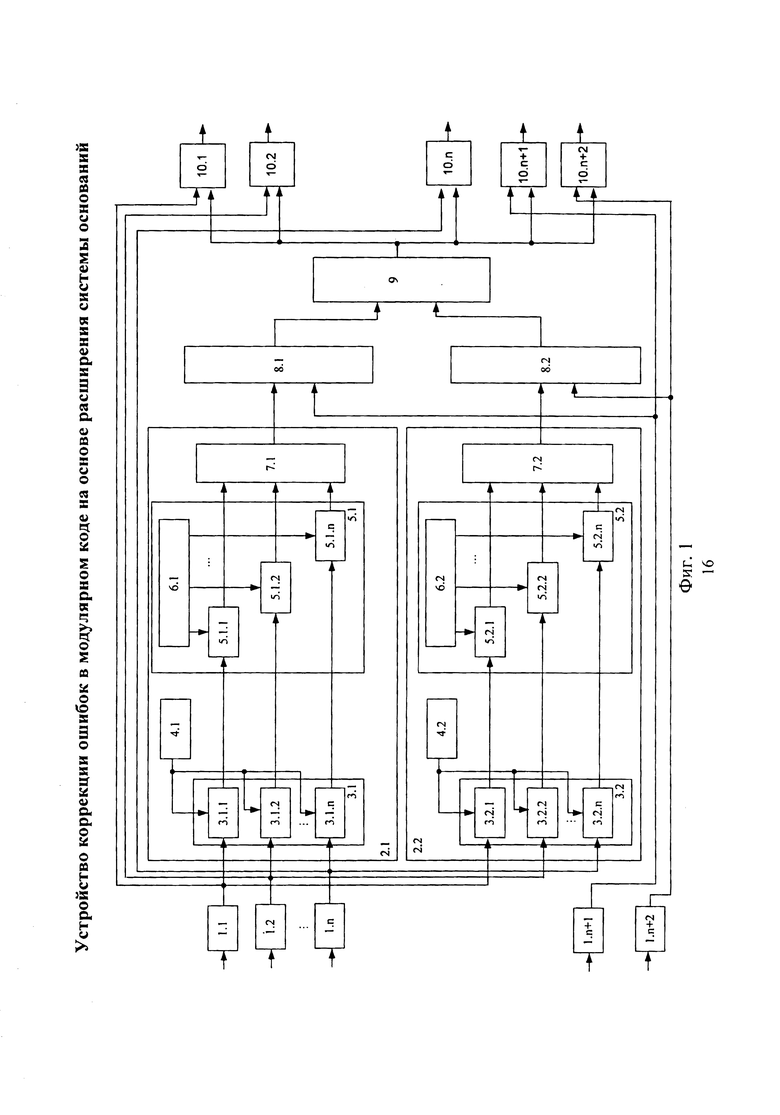
Структура устройства коррекции ошибок в модулярном коде на основе расширения системы оснований представлена на фиг. 1.
Устройство содержит блок регистров, состоящий из n+2 регистров 1.1, …, 1.n+2, который подключен к входу устройства, на который подается код ПСКВ. Регистры предназначены для хранения остатков кода ПСКВ. Для вычисления остатков по контрольным основаниям используется блок 2.1 вычисления первого контрольного остатка и блок 2.2 вычисления второго контрольного остатка. Структура этих блоков одинаковая. Каждый из блоков содержит первый 3.m блок умножителей, где m=1, 2, в состав которого входят n умножителей по модулю pi(z) 3.m.i, где i=1, 2, …, n, первый блок 4.m памяти для хранения ортогональных весов mi(z); второй блок умножителей 5.m, который содержит n умножителей по модулю pn+m(z), второй блок памяти 6.m для хранения 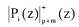 , сумматор 7.m по модулю два. Устройство содержит также два сумматора вычисления синдрома ошибки 8.1 и 8.2, блок памяти 9, предназначенный для хранения вектора ошибки, n+2 корректирующих сумматора 10.1, …, 10.n+2, выходы которых являются выходом устройства.
, сумматор 7.m по модулю два. Устройство содержит также два сумматора вычисления синдрома ошибки 8.1 и 8.2, блок памяти 9, предназначенный для хранения вектора ошибки, n+2 корректирующих сумматора 10.1, …, 10.n+2, выходы которых являются выходом устройства.
Причем вход устройства подключен к входам регистров 1.1, …, 1.n+2. Выход i-го регистра 1.i, где i=1, 2, …, n, предназначенного для хранения информационного остатка αi(z), подключен к первому входу соответствующего умножителя по модулю pi(z) 3.1.i блока 2.1 вычисления первого контрольного основания и 3.2.i блока 2.2 вычисления второго контрольного основания. Ко второму входу этих умножителей по модулю pi(z) 3.1.i и 3.2.i соответственно подключены выходы первых блоков памяти 4.1 и 4.2. Выходы умножителей по модулю pi(z) 3.1.i и 3.2.i подключены соответственно к первым входам умножителей 5.1.i по модулю pn+1(z) и 5.2.i по модулю pn+2(z), входящих в состав второго блока умножителей 5.1 и 5.2 соответственно. Вторые входы умножителей 5.1.i по модулю pn+1(z) и 5.2.i по модулю pn+2(z) соединены с выходами второго блока памяти 6.1 и 6.2, а выходы подключены к входам сумматора по модулю два 7.1 и 7.2 блока 2.1 вычисления первого контрольного основания и блока 2.2 вычисления второго контрольного основания. Выходы сумматоров по модулю два 7.1 и 7.2 соответственно подключены к первым входам сумматоров вычисления синдрома ошибки 8.1 и 8.2, вторые входы которых соединены с выходами регистров 1.n+1 и 1.n+2. Выходы сумматоров вычисления синдрома ошибки 8.1 и 8.2 подключены соответственно к входам блока памяти 9, выходы которого подключены соответственно ко вторым входам корректирующих сумматоров 10.1, …, 10.n+2. Первые входы корректирующих сумматоров 10.1 …, 10.n+2 подключены к соответствующим выходам регистров 1.1-1.n+2. Выход корректирующих сумматоров 10.1, …, 10.n+2 являются выходом устройства.
Устройство работает следующим образом. На вход устройства поступает модулярный код α1(z), α2(z), …, αn(z), αn+1(z), αn+2(z). Данные остатки записываются в регистры 1.1-1.n+2. Информационный остаток αi(z), где i=1, 2, …, n с выхода регистра 1.i подается на первый вход умножителя 3.1.i, первого блока 3.1 умножителей блока 2.1 вычисления первого контрольного остатка и на первый вход умножителя 3.2.i, первого блока 3.2 умножителей блока 2.2 вычисления второго контрольного остатка. На второй вход умножителя по модулю pi(z) 3.1.i и 3.2.i подается с выходов первых блоков памяти 4.1 и 4.2 значения базиса mi(z). С выхода умножителя по модулю pi(z) 3.1.i и 3.2.i соответственно первого блока умножителей 3.1 и 3.2 снимаются значения αi(z)mi(z)modpi(z), которые затем подаются на первый вход умножителя по модулю pn+1(z) 5.1.i второго блока умножителей 5.1 и вход умножителя по модулю pn+2(z) 5.2.i второго блока умножителей 5.2. На вторые входы этих умножителей, выполняющих умножение по модулю pn+1(z) и pn+2(z) соответственно, поступают значения 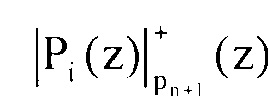 , и
, и 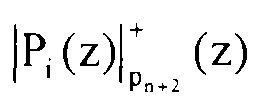 , которые хранились в втором блоке памяти 6.1 и 6.2. С выхода умножителя по модулю pn+1(z) 5.1.i, второго блока умножителей 5.1 блока 2.1 вычисления первого контрольного остатка снимается значение
, которые хранились в втором блоке памяти 6.1 и 6.2. С выхода умножителя по модулю pn+1(z) 5.1.i, второго блока умножителей 5.1 блока 2.1 вычисления первого контрольного остатка снимается значение
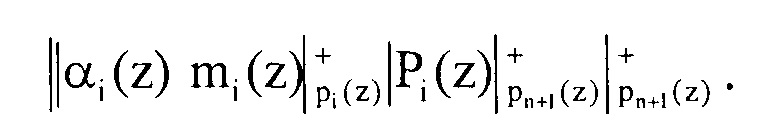
С выхода умножителя по модулю pn+2(z) 5.2.i, второго блока умножителей 5.2 блока 2.2 вычисления второго контрольного остатка снимается значение

Вычисленные значения произведения соответственно подаются на входы сумматора 7.1 и 7.2 по модулю 2. На выходе сумматора 7.1 по модулю два блока 2.1 вычисления первого контрольного остатка появляется значение остатка 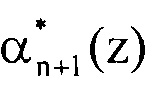 в расширенной системе оснований. На выходе сумматора 7.2 по модулю два блока 2.2 вычисления второго контрольного остатка появляется значение остатка
в расширенной системе оснований. На выходе сумматора 7.2 по модулю два блока 2.2 вычисления второго контрольного остатка появляется значение остатка 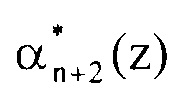 в расширенной системе оснований.
в расширенной системе оснований.
Вычисленное значение остатка 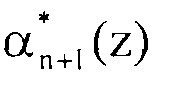 поступает на первый вход сумматора 8.1 вычисления синдрома ошибки. На второй вход сумматора 8.1 вычисления синдрома с выхода регистра 1.n+1 подается значение контрольного основания
поступает на первый вход сумматора 8.1 вычисления синдрома ошибки. На второй вход сумматора 8.1 вычисления синдрома с выхода регистра 1.n+1 подается значение контрольного основания 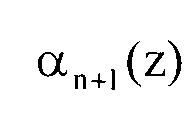 , комбинации поступившей на вход устройства.
, комбинации поступившей на вход устройства.
Вычисленное значение остатка  поступает на первый вход сумматора 8.2 вычисления синдрома ошибки. На второй вход сумматора 8.1 вычисления синдрома с выхода регистра 1.n+2 подается значение контрольного основания αn+2(z), комбинации, поступившей на вход устройства.
поступает на первый вход сумматора 8.2 вычисления синдрома ошибки. На второй вход сумматора 8.1 вычисления синдрома с выхода регистра 1.n+2 подается значение контрольного основания αn+2(z), комбинации, поступившей на вход устройства.
С выхода сумматора 8.1 вычисления синдрома ошибки значение синдром ошибки S1 поступает на первый вход блока памяти 9. С выхода сумматора 8.2 вычисления синдрома ошибки значение синдром ошибки S2 поступает на второй вход блока памяти 9. С выхода блока памяти 9 снимается значение, которое предназначено для исправления ошибки в коде ПСКВ. Данное значение поступает на вторые входы корректирующих сумматоров по модулю два 10.1, …, 10.n+2. На первые входы этих сумматоров по модулю два 10.1, …, 10.n+2 подаются значения остатков кода ПСКВ α1(z), α2(z), …, αn(z), αn+1(z), αn+2(z) с выходов регистров 1.1, …, 1.n+2 соответственно. С выходов сумматоров по модулю два 10.1, …, 10.n+2 откорректированный код ПСКВ подается на выход устройства.
Рассмотрим пример. Пусть задано расширенное поле Галуа GF(24), в котором определены информационные основания pi(z)=z+1, p2(z)=z2+z+1, p3(z)=z4+z3+z2+z+1, расширяем систему оснований за счет введения двух контрольных оснований p4(z)=z4+z3+1 и р5(z)=z4+z+1. В этом случае  .
.
При этом полный диапазон составляет:
Рполн(z)=z15+1.
Рконт45(z)=z8+z7+z5+z4+z3+z+1.
Определим значения рабочих оснований Pi(z) и mi(z):
P1(z)=p2(z)⋅p3(z)=z6+z4+z3+z2+1
P2(z)=p1(z)⋅p3(z)=z5+1
P3(z)=p1(z)⋅p2(z)=z3+1,
m1(z)=1; m2(z)=z+1; m3(z)=z2+z+1.
Следовательно, ортогональные базисы Вi(z) соответственно равны
B1(z)=m1(z)⋅P1(z)=z6+z4+z3+z2+1;
B2(z)=m2(z)⋅P2(z)=z6+z5+z+1;
B3(z)=m3(z)⋅P3(z)=z5+z4+z3+z2+z+1.
Воспользуемся полином A(z)=z6. В модулярном коде полином представляет A(z)=(1, 1, z).
Расширяем систему оснований за счет введения двух контрольных оснований p4(z)=z4+z3+1 и p5(z)=z4+z+1.
Первое основание расширения системы pn+1(z)=р4(z)=z4+z3+1
Вычислим значения Pi(z)modp4(z). Тогда имеем
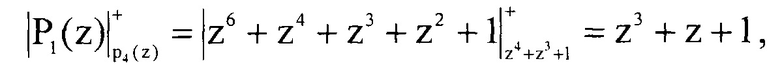
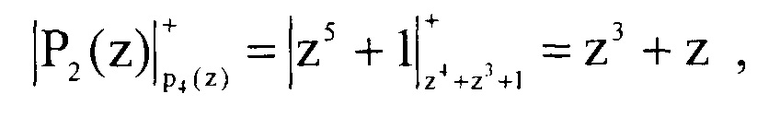
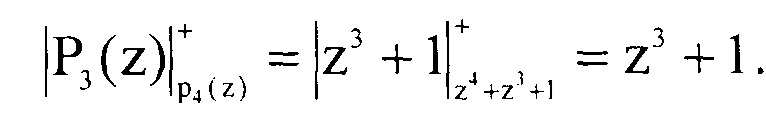
Определим произведение 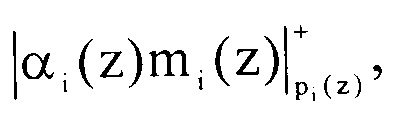 они соответственно равны
они соответственно равны
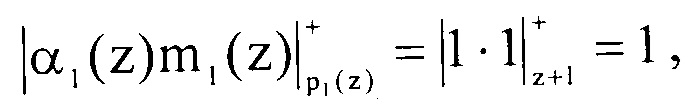
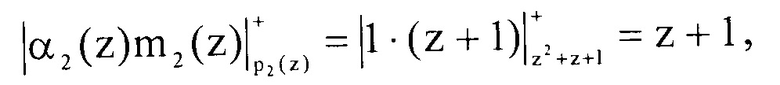
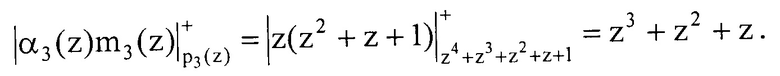
Подставляем полученные значения в выражение (7)
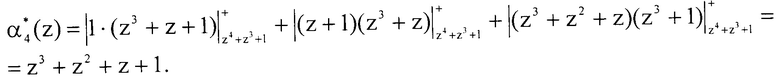
Результат расширения по основанию pn+1(z)=p4(z)=z4+z3+1 получили остаток α4(z)=z3+z2+z+1. Проведем проверку и определим остаток исходного полинома
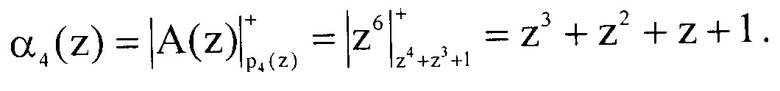
Второе основание расширения pn+2(z)=p5(z)=z4+z+1.
Вычислим значения Pi(z)modp5(z). Тогда имеем
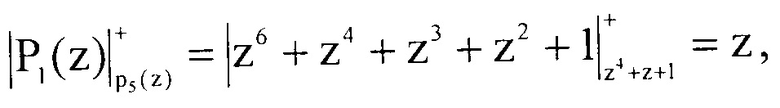
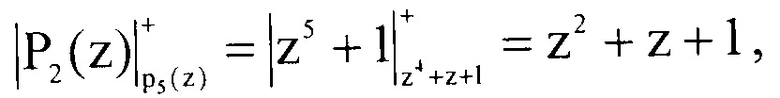
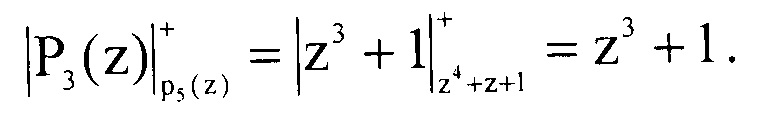
Определим произведение 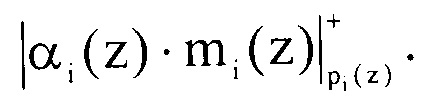 Они соответственно равны
Они соответственно равны


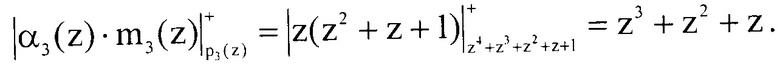
Подставляем полученные значения в выражение (8)
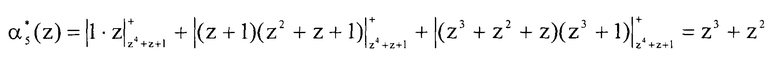
Результат расширения по основанию pn+2(z)=p5(z)=z4+z+1 - остаток α5(z)=z3+z2. Проведем проверку и определим остаток исходного полинома
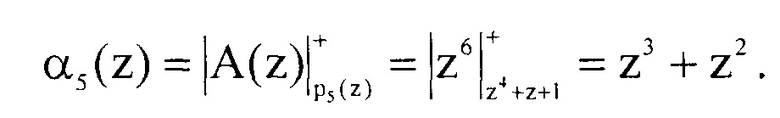
Таким образом, расширенная комбинация избыточного кода ПСКВ будет иметь вид
A(z)=(1, 1, z, z3+z2, z3+z2+z+1).
Если на вход устройства и обнаружения ошибки, использующего разработанный алгоритм расширения системы оснований, поступит A(z)=(1, 1, z, z3+z2, z3+z2+z+1), то синдром ошибки будет равен
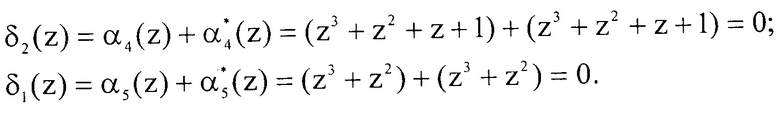
Так как синдром ошибки равен нулю, следовательно, проверяемая комбинация кода ПСКВ не содержит ошибки.
Рассмотрим ситуацию, когда проверяемая комбинация ПСКВ содержит ошибку по первому основанию и ее глубина равна Δα(z)=1. Тогда значение первого остатка равно Ошибочная комбинация модулярного кода ПСКВ имеет вид
Ошибочная комбинация модулярного кода ПСКВ имеет вид
A*(z)=(0, 1, z, z3+z2,z3+z2+z+1).
Определим произведение 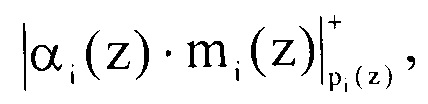 для данной ошибочной комбинации кода ПСКВ
для данной ошибочной комбинации кода ПСКВ
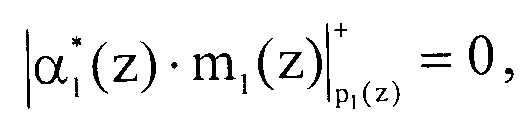
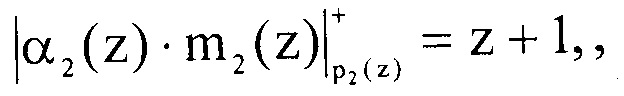
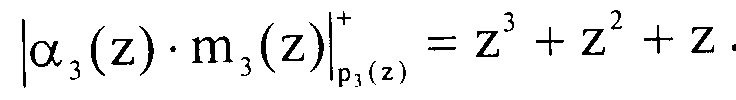
Вычислим первый контрольный остаток, подставив значения в выражение (7)
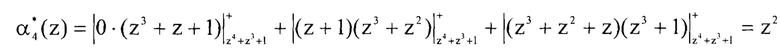
Результатом расширения по основанию pn+1(z)=p4(z)=z4+z3+1 является остаток 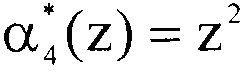 .
.
Вычислим второй контрольный остаток, подставив значения в выражение (8)

Результатом расширения по основанию pn+2(z)=p5(z)=z4+z+1 является остаток 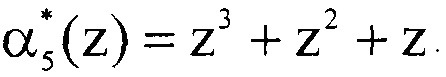
Выполним проверку комбинации путем вычисления синдрома ошибки, имеем
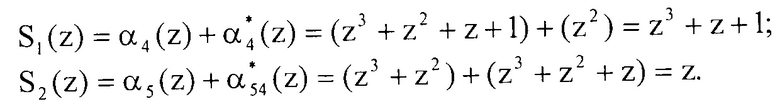
Проверяемая комбинация содержит ошибки, так как синдром ошибки отличен от нуля. В таблице 1 приведены значения глубины и местоположения ошибки в коде ПСКВ по рабочим основаниям и соответствующего им синдрома ошибки S1(z) и S2(z). Данные в таблице приведены в шестнадцетеричной системе счисления. По значению синдрома ошибки определяем, что ошибка произошла по первому основанию p1(z)=z+1, а ее глубина равна Δαi(z)=1. Значит, вектор ошибки будет равен e(z)=(1, 0, 0, 0, 0).
Для коррекции ошибки необходимо данный вектор ошибки сложить с ошибочной комбинацией кода ПСКВ. Имеем
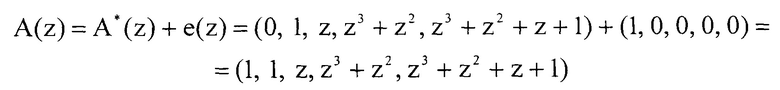

Если ошибка произойдет по первому контрольному основанию p4(z)=z4+z3+1, то значение первой составной синдрома S1(z) будет показывать глубину ошибки, а значение S2(z) будет равняться нулю.
Если ошибка произойдет по второму контрольному основанию p5(z)=z4+z+1, то значение второй составной синдрома S2(z) будет показывать глубину ошибки, а значение первой составляющей синдрома S1(z) будет равняться нулю.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С ПЕРЕСЧЕТОМ ОРТОГОНАЛЬНЫХ БАЗИСОВ | 2005 |
|
RU2298873C1 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2409840C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ | 2014 |
|
RU2560823C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2013 |
|
RU2513915C1 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2010 |
|
RU2453902C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССА ВЫЧЕТОВ | 2004 |
|
RU2267808C2 |
Изобретение относится к вычислительной технике и, в частности к непозиционным компьютерам. Технический результат заключается в обеспечении коррекции ошибок в кодовой комбинации ПСКВ на основе выполнения операции расширения оснований. Технический результат достигается за счет введения блока регистров, состоящих из n+2 регистров, предназначенных для хранения остатков, где n - количество информационных оснований ПСКВ, n+1 и n+2 - контрольные основания ПСКВ, блока вычисления второго контрольного остатка, структура которого соответствует структуре прототипа, двух сумматоров вычисления синдрома ошибки, блока памяти, предназначенного для хранения вектора ошибки, n+2 корректирующих сумматоров, с помощью которых происходит исправление ошибки по модулю два. 1 ил.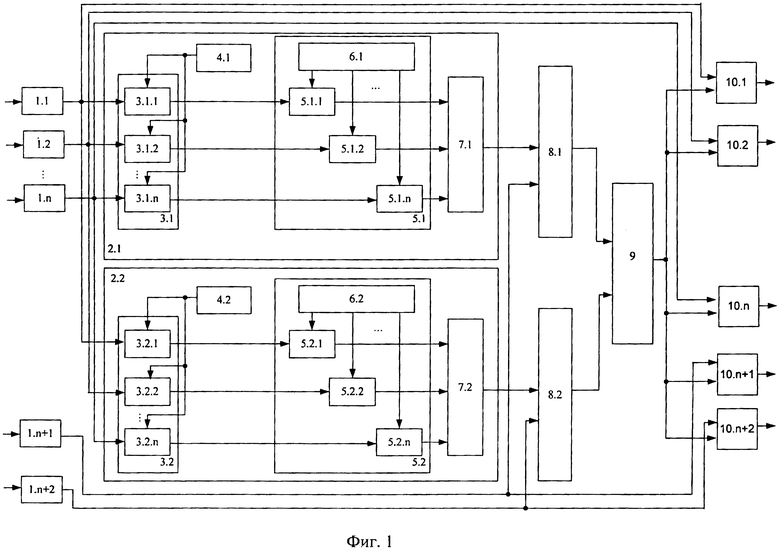
Устройство коррекции ошибок в модулярном коде на основе расширения системы оснований содержит первый блок умножителей, который содержит n умножителей по модулю pi(z), где i=1, 2, …, n, первый блок памяти, для хранения ортогональных весов mi(z), второй блок умножителей, который содержит n умножителей по модулю pn+1(z), второй блок памяти для хранения  , сумматор по модулю два, которые входят в состав блока вычисления первого контрольного остатка, при этом на первый вход i-го умножителя по модулю pi(z) первого блока умножителей подается остаток αi(z) кода полиномиальной системы классов вычетов ПСКВ, второй вход i-го умножителя по модулю pi(z) соединен с выходом первого блока памяти, а выход i-го умножителя по модулю pi(z) подключен к первому входу i-го умножителя по модулю pn+1(z) второго блока умножителей, при этом второй вход умножителя по модулю pn+1(z) подключен к выходу второго блока памяти, выходы умножителей второго блока умножителей подсоединены к входам сумматора по модулю два, отличающееся тем, что в устройство введены блок вычисления второго контрольного остатка, структура которого аналогична блоку вычисления первого контрольного остатка, n+2 регистра, предназначенных для хранения остатков (α1(z), α2(z), …, αn(z), αn+1(z), αn+2(z)) кода ПСКВ, два сумматора вычисления синдрома ошибки, блок памяти, предназначенный для хранения вектора ошибки, n+2 корректирующих сумматора, выходы которых являются выходом устройства, входы регистров подключены к входу устройства, на который поступает код ПСКВ, выход i-го регистра подключен к первому входу i-го умножителя по модулю pi(z) блока вычисления первого контрольного остатка и блока вычисления второго контрольного остатка, а выходы сумматоров по модулю два блока вычисления первого контрольного остатка и блока вычисления второго контрольного остатка подключены соответственно к первым входам первого и второго сумматоров вычисления синдрома ошибки, второй вход первого сумматора вычисления синдрома ошибки подключен к выходу (n+1)-го регистра, второй вход второго сумматора вычисления синдрома ошибки подключен к выходу (n+2)-го регистра, выходы сумматоров вычисления синдрома ошибки подключены к входам блока памяти, выходы которого подключены соответственно ко вторым входам n+2 корректирующих сумматоров, первые входы j-го корректирующего сумматора, где j=1, …, n+2, подключены к выходу j-го регистра, выход корректирующих сумматоров являются выходом устройства.
, сумматор по модулю два, которые входят в состав блока вычисления первого контрольного остатка, при этом на первый вход i-го умножителя по модулю pi(z) первого блока умножителей подается остаток αi(z) кода полиномиальной системы классов вычетов ПСКВ, второй вход i-го умножителя по модулю pi(z) соединен с выходом первого блока памяти, а выход i-го умножителя по модулю pi(z) подключен к первому входу i-го умножителя по модулю pn+1(z) второго блока умножителей, при этом второй вход умножителя по модулю pn+1(z) подключен к выходу второго блока памяти, выходы умножителей второго блока умножителей подсоединены к входам сумматора по модулю два, отличающееся тем, что в устройство введены блок вычисления второго контрольного остатка, структура которого аналогична блоку вычисления первого контрольного остатка, n+2 регистра, предназначенных для хранения остатков (α1(z), α2(z), …, αn(z), αn+1(z), αn+2(z)) кода ПСКВ, два сумматора вычисления синдрома ошибки, блок памяти, предназначенный для хранения вектора ошибки, n+2 корректирующих сумматора, выходы которых являются выходом устройства, входы регистров подключены к входу устройства, на который поступает код ПСКВ, выход i-го регистра подключен к первому входу i-го умножителя по модулю pi(z) блока вычисления первого контрольного остатка и блока вычисления второго контрольного остатка, а выходы сумматоров по модулю два блока вычисления первого контрольного остатка и блока вычисления второго контрольного остатка подключены соответственно к первым входам первого и второго сумматоров вычисления синдрома ошибки, второй вход первого сумматора вычисления синдрома ошибки подключен к выходу (n+1)-го регистра, второй вход второго сумматора вычисления синдрома ошибки подключен к выходу (n+2)-го регистра, выходы сумматоров вычисления синдрома ошибки подключены к входам блока памяти, выходы которого подключены соответственно ко вторым входам n+2 корректирующих сумматоров, первые входы j-го корректирующего сумматора, где j=1, …, n+2, подключены к выходу j-го регистра, выход корректирующих сумматоров являются выходом устройства.
| УСТРОЙСТВО РАСШИРЕНИЯ ОСНОВАНИЙ МОДУЛЯРНОГО КОДА | 2014 |
|
RU2562366C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| Устройство для централизованного управления затворами силосов, амбаров и т.п. | 1930 |
|
SU27610A1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
Авторы
Даты
2018-04-26—Публикация
2017-07-24—Подача