Предлагаемое изобретение относится к области спутниковой навигации и может быть использовано для определения углового положения объектов в пространстве или на плоскости.
Известен способ угловой ориентации по сигналам космических аппаратов глобальных навигационных спутниковых систем, основанный на приеме сигналов на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами на разнесенные антенны от каждого космического аппарата и определении углового положения осей измеряемого объекта путем решения системы уравнений [Лукин В. Н., Мищенко И.Н., Новиков И.А. Использование системы NAVSTAR для определения угловой ориентации объектов. /Зарубежная радиоэлектроника N 1, 1991].
Недостатком способа является низкая точность измерения углов, обусловленная тем, что антенны необходимо располагать на малом расстоянии, меньшем длины волны принимаемых сигналов. При увеличении расстояния между фазовыми центрами разнесенных антенн погрешность измерения углов уменьшается, но появляется неоднозначность фазовых измерений, что приводит к неоднозначному определению углового положения объекта. Для устранения неоднозначности применяется более сложная обработка сигналов, заключающаяся в проведении измерений по различным спутникам и обработке результатов измерений фазовых сдвигов с помощью фильтра Калмана, позволяющего отбраковать ложные гипотезы. При этом существенное значение имеет время сходимости решения задачи. Время сходимости, т. е. время, требуемое для определения угловой ориентации может быть достаточно велико. Так при четырех космических аппаратах и геометрическом факторе 5.5 и 3.7 время сходимости системы уравнений даже при использовании быстродействующей ЭВМ составляет соответственно 1600 и 400 с, т. е. является очень большим. Определение угловой ориентации объекта в условиях наличия систематических погрешностей приводит к еще большему увеличению времени, требуемого на решение системы уравнений.
Известен также способ определения курсового угла и координат местоположения объектов по радионавигационным сигналам космических аппаратов, основанный на приеме сигналов от n космических аппаратов двумя или более антенно-приемными устройствами, расположенными параллельно одной или двум осям объекта, выделении сигналов с частотой Доплера, определении набега фаз за интервал времени измерения и определении углового положения осей объекта [Патент РФ, N 2022294. Опубл. БИ N 20. 1994].
Недостатком способа является длительное время измерений, необходимое для определения углового положения с погрешностью, не превышающей заданную. Это связано с тем, что для определения угловой ориентации с заданной точностью необходимо, чтобы космические аппараты, излучающие сигналы, за время измерения достаточно переместились в пространстве. Необходимое время составляет 30 - 60 минут, что для многих применений оказывается недопустимым.
В основу изобретения положена задача уменьшения погрешности определения угловой ориентации осей объектов по радионавигационным сигналам космических аппаратов при заданном времени измерения
Поставленная задача решается тем, что в способе угловой ориентации объекта по радионавигационным сигналам космических аппаратов по варианту 1, основанном на приеме сигналов от n космических аппаратов двумя или более антенно-приемными устройствами, расположенными параллельно одной или двум осям объекта, выделении сигнала с частотой Доплера, определении набега фаз за интервал времени измерения и определении углового положения объекта, согласно изобретению, в течение интервала времени измерения производят m измерений фазовых сдвигов между парами антенно-приемных устройств, а угловое положение объекта определяют путем решения следующей системы уравнений: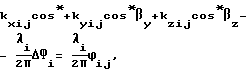
где
i = 1,...n; j = 1,..., m;
cos*βxyz= B•cosβxyz - произведение неизвестной базы B (расстояния между антенно-приемными устройствами) на ее направляющие косинусы cosβxyz, подлежащие определению;
kxij, kyij, kzij - направляющие косинусы направлений потребитель - i-тый навигационный космический аппарат (НКА);
λi - длина волны сигнала i-го НКА;
ϕij - измеренные значения фазовых сдвигов сигналов i-го НКА, принятых антеннами потребителя в j-м измерении;
ΔФi - неизвестная систематическая погрешность измерений разности фаз, обусловленная разным временем прохождения сигналов в каналах приемоиндикатора и неоднозначностью, вызванной тем, что расстояние между антеннами превышает длины волн принимаемых сигналов.
Решение поставленной задачи также достигается тем, что в способе угловой ориентации объекта по радионавигационным сигналам космических аппаратов по варианту 2, основанном на приеме сигналов от n космических аппаратов двумя или более антенно-приемными устройствами, расположенными параллельно одной или двум осям объекта, выделении сигнала с частотой Доплера, определении набега фаз за интервал времени измерения и определении углового положения объекта, согласно изобретению в течение интервала времени измерения производят m измерений фазовых сдвигов между парами антенно-приемных устройств, вычисляют разности фазовых сдвигов принятых сигналов в (m/2 + j)-м и j-м измерениях, а угловое положение объекта определяют путем решения следующей системы уравнений: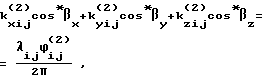
где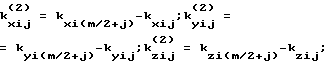
ϕ
Решение поставленной задачи также достигается тем, что в способе угловой ориентации объекта по радионавигационным сигналам космических аппаратов по варианту 3, основанном на приеме сигналов от n космических аппаратов двумя или более антенно-приемными устройствами, расположенными параллельно одной или двум осям объекта, выделении сигнала с частотой Доплера, определении набега фаз за интервал времени измерения и определении углового положения объекта, согласно изобретению в течение интервала времени измерения производят m измерений фазовых сдвигов между парами антенно-приемных устройств, вычисляют разности сумм фазовых сдвигов, накопленных в интервалах (1, ..., m/2) и (m/2 + 1, ..., m) измерений, а угловое положение объекта определяют путем решения следующей системы уравнений: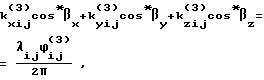
где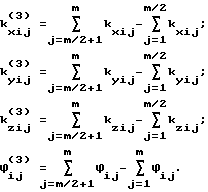
Решение поставленной задачи также достигается тем, что в способе угловой ориентации объекта по радионавигационным сигналам космических аппаратов по варианту 4, основанном на приеме сигналов от n космических аппаратов двумя или более антенно-приемными устройствами, расположенными параллельно одной или двум осям объекта, выделении сигнала с частотой Доплера, определении набега фаз за интервал времени измерения и определении углового положения объекта, согласно изобретению в течение интервала времени измерения производят m измерений фазовых сдвигов между парами антенно-приемных устройств, вычисляют разности фазовых сдвигов принятых сигналов в (m-j)-m и j-м измерениях, а угловое положение объекта определяют путем решения следующей системы уравнений: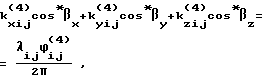
где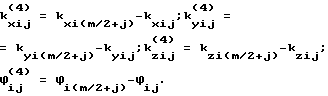
Сущность предлагаемого способа можно пояснить следующим образом.
При определении угловых координат объектов используют результаты косинусов углов αi между вектором - базой и вектором - направлением на i-тый навигационный космический аппарат (НКА) глобальных навигационных спутниковых систем.
Фазовый сдвиг сигнала i-го НКА, принимаемого двумя пространственно разнесенными антеннами и косинус угла между вектором-базой и вектором-направлением на НКА связаны выражением: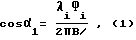
где
i = 1, n; n - общее число НКА, используемых для определения ориентации объекта:
λi - длина волны сигнала i-го НКА:
Фi - фазовый сдвиг сигналов, принятых разнесенными антеннами:
B - расстояние между антеннами;
Вычисления направляющих косинусов вектора-базы осуществляют на основе уравнения, полученного исходя из свойства скалярного произведения векторов в декартовой системе координат: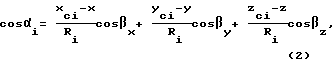
где
x, y, z - координаты потребителя в геоцентрической системе координат (ГЦСК);
xci, yci, zci - координаты i-го спутника в ГЦСК;
cosβx,cosβy,cosβz - - направляющие косинусы вектора-базы;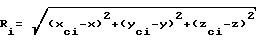 - расстояние между потребителем и i-тым НКА;
- расстояние между потребителем и i-тым НКА;
Введем обозначения: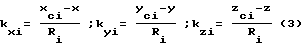
Коэффициенты kxi,yi,zi являются направляющими косинусами векторов-направлений между потребителем и i-тым НКА, cosβx,cosβy,cosβz - направляющие косинусы вектора-базы, представляющие собой координаты векторов единичной длины, по направлению совпадающего с базой.
С учетом принятых обозначений система уравнений (2) запишется следующим образом: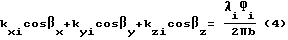
Систему уравнений (4) можно дополнить нелинейным уравнением связи между направляющими косинусами, которое имеет вид:
(cosβx)2+(cosβy)2+(cosβx)2= 1 (5)
При определении угловых координат потребителя часто неизвестными являются не только направляющие косинусы вектора-базы, но и сама величина базы B. При этом выражения (4) и (5) запишутся следующим образом: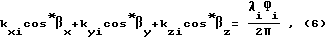
(cos*βx)2+(cos*βy)2+(cos*βz)2= B2, (7)
где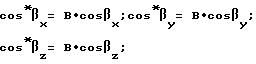
Величины cos*βx;cos*βy,cos*βz являются геоцентрическими координатами фазового центра второй антенны относительно фазового центра первой антенны.
В дальнейших материалах заявки рассматриваются решение системы уравнений (6) и определение относительных координат второй антенны с последующим нахождением направляющих косинусов вектора-базы и расстояния между антенно-приемными устройствами B при помощи уравнения (7).
Как правило, при определении углового положения вектора-базы в целях повышения точности используют интерферометры с размером базы, существенно превышающим длины волн принимаемых сигналов. Так, например, длина волны НКА спутниковой радионавигационной системы ГЛОНАСС составляет около 20 см, величина базы может быть около 2 м. Реальная фазоизмерительная аппаратура имеет диапазон однозначных измерений в пределах 180o или 360o, т. е. λ/2 или λ. Кроме того, при измерениях фазовых сдвигов возникают аппаратурные систематические погрешности, обусловленные разным временем прохождения принятых сигналов в антенно-приемных устройствах. В связи с этим выражение для полного фазового сдвига принятых сигналов можно записать в виде
Фi= 2πki+Δϕci+ϕi, (8)
где
ki - число целых циклов неоднозначности 360o в полной разности фаз сигнала i-го НКА;
/Δϕci - не зависящая от времени аппаратурная систематическая погрешность измерения фазового сдвига сигнала i-го НКА.
ϕi - измеренное значение разности фаз сигналов i-го НКА, принятых на 2 антенны интерферометра.
С учетом наличия систематической погрешности и неоднозначности система уравнений (6) примет вид: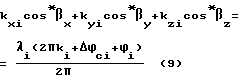
Система уравнений (9) записана для одного момента измерений по n НКА. При проведении ряда разновременных измерений система примет вид: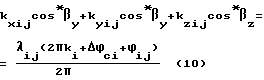
Система (10) записана при условии, что измерения выполняются путем непрерывного слежения за фазовыми сдвигами принятых сигналов. Исходя из этого величина ki не зависит от номера измерения j и является начальной неоднозначностью для первого измерения фазового сдвига сигнала i-го НКА.
Также можно считать, что длины волн принятых сигналов не меняются в процессе измерений. Частота принятых сигналов меняется с течением времени за счет эффекта Доплера, при этом относительное изменение частоты сигнала спутника за время нахождения его в зоне радиовидимости определяется соотношением: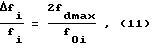
где
fdmax - максимальное значение доплеровского сдвига частоты принятых сигналов. Для неподвижного потребителя эта величина не превысит 5000 Гц;
fOi- значение несущей частоты сигнала i-го спутника.
Так для спутниковой радионавигационной системы ГЛОНАСС значения несущих частот НКА располагаются в диапазоне 1602.5625 - 1615.5 МГц, для оценки относительного изменения частоты можно принять fOi = 1610 МГц. В системе GPS все НКА излучают сигналы с частотой 1575.42 МГц.
Таким образом относительное изменение частоты сигналов составляет 6.21•10-6 и 6.34•10-6 для систем ГЛОНАСС и GPS соответственно. Как видим, относительное изменение частоты сигнала за время пролета НКА невелико и практически не внесет изменения в длины волн принятых сигналов, поэтому можно считать λij= λi= const, не зависящей от j.
Для упрощения дальнейшего изложения объединим не зависящие от времени неоднозначность 2πki и аппаратурную составляющую систематической погрешности Δϕci/ и перенесем их в левую часть системы (10).
С учетом вышеприведенных упрощений система (10) запишется в виде: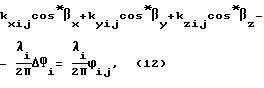
где
ΔФi= 2πki+Δϕi - систематическая погрешность измерения фазового сдвига сигнала i-го НКА.
Система уравнений (12) содержит n•m уравнений с n+3 неизвестными. Неизвестными в системе (12) являются относительные координаты антенны A2 по отношению к Al - cos*βx,cos*βy,cos*βz, а также систематические погрешности измерения фазовых сдвигов по каждому из спутников ΔФ1,ΔФ2,...ΔФn.
Определение угловой ориентации по варианту 1 производится путем проведения m последовательных измерений фазовых сдвигов принятых сигналов путем решения системы уравнений (12). При этом помимо угловой ориентации объектов выполняется оценка систематических погрешностей измерения фазовых сдвигов по сигналам каждого из спутников.
С целью уменьшения числа неизвестных и облегчения решения система (12) может быть преобразована при помощи перехода к различным комбинациям разностей уравнений, взятых в разные моменты времени. При этом из числа неизвестных исключаются систематические погрешности измерений ΔФ1,ΔФ2,...ΔФn, поскольку они не меняются во времени.
Решение поставленной задачи по варианту 2 достигается тем, что после проведения m измерений фазовых сдвигов между парами антенно-приемных устройств вычисляют разности фазовых сдвигов принятых сигналов в (m/2 + j)-м и j-м измерениях. Система уравнений для определения угловой ориентации в этом случае имеет вид: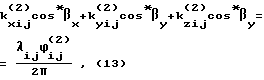
где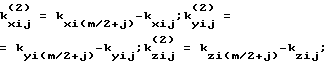
ϕ
Решение поставленной задачи по варианту 3 достигается тем, что после проведения m измерений фазовых сдвигов между парами антенно-приемных устройств вычисляют разности сумм фазовых сдвигов накопленных в интервалах (1, . . ., m/2) и (m/2 + 1, ..., m) измерений. Система уравнений для определения угловой ориентации в этом случае имеет вид: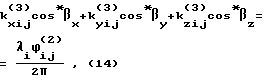
где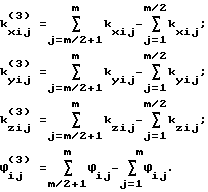
Решение поставленной задачи по варианту 4 достигается тем, что после проведения m измерений фазовых сдвигов между парами антенно-приемных устройств вычисляют разности фазовых сдвигов принятых сигналов в (m-j)-м и j-м измерениях. Система уравнений для определения угловой ориентации в этом случае имеет вид: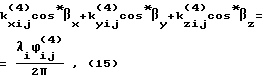
где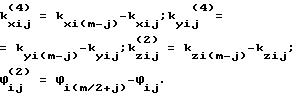
В результате решения систем (12) - (15) получают относительные координаты фазового центра второй антенны 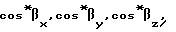 по которым с использованием уравнения (7) определяют расстояние между антеннами B, и осуществляют переход к направляющим косинусам оси объекта по формулам:
по которым с использованием уравнения (7) определяют расстояние между антеннами B, и осуществляют переход к направляющим косинусам оси объекта по формулам: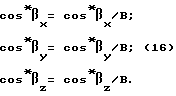
На чертеже приведена структурная схема устройства, реализующего предложенный способ.
Устройство содержит антенны 1, 2, расположенные параллельно осевой линии объекта, последовательно соединенные с ними малошумящие усилители (МШУ) 3, 4, радиотракты 5, 6, блоки цифровой обработки сигналов 7, 8, формирователь опорных сигналов 9, включающий в себя синтезатор частот и генератор псевдослучайной последовательности (ПСП), подключенный ко вторым входам радиотрактов 5, 6 и блоков цифровой обработки 7, 8, опорный генератор 10, первый выход которого подключен ко входу формирователя опорных сигналов 9, а второй выход - к входу синхронизации вычислительного процессора 11, на информационные входы которого поступают сигналы с блоков цифровой обработки 7 и 8.
Сигналы n НКА принимаются двумя разнесенными антеннами 1 и 2, усиливаются малошумящими усилителями 3 и 4, преобразуются в сигналы промежуточной частоты и усиливаются радиотрактами 5 и 6 и затем поступают в блоки цифровой обработки сигналов 7 и 8, где происходит разделение сигналов каждого из спутников. Блоки цифровой обработки 7 и 8 реализованы по схеме оптимального корреляционного приемника, на выходе которых формируются отсчеты корреляционных интегралов I и Q для сигналов, каждого из НКА, которые соответствуют результатам корреляционного перемножения принимаемых сигналов на синфазную и ортогональную составляющие опорного сигнала, формируемые генератором опорных сигналов 9 для каждого из спутников. На вычислительный процессор 11 возложены функции управления режимами работы приемника, включающими в себя поиск, захват сигналов по частоте и задержке, частотную и фазовую автоподстройку, синхронизацию по метке времени и границе бита служебной информации, прием и декодирование служебной информации и измерение радионавигационных параметров сигнала. К радионавигационным параметрам сигнала относятся его задержка, частота и фаза. Кроме управления режимами работы и измерения радионавигационных параметров вычислительный процессор 11 решает задачи вторичной обработки измеренных параметров, заключающиеся в определении координат НКА на момент проведения измерений (задача размножения эфемерид) на основе принятой служебной информации, вычисления координат места потребителя и определения угловой ориентации антенной платформы. Также на вычислительный процессор 11 возложена задача прогноза сеансов навигационных определений и управления режимами работы блоков 7 и 8 для НКА, появляющихся или покидающих зону радиовидимости.
Координаты места потребителя определяются на основе измерений задержек сигналов, принятых с борта каждого НКА. Для проведения таких измерений сигналы каждого НКА модулируются псевдослучайными последовательностями (ПСП), называемыми дальномерным кодом. Путем сравнения ПСП сигнала, сформированного блоком 9, с ПСП принятого сигнала происходит определение времени задержки принятого сигнала. Дальность до НКА, излучившего сигнал, получают путем умножения времени задержки на скорость распространения радиосигналов. Следует отметить, что, вследствие несовпадения бортового времени потребителя с опорным временем спутниковой радионавигационной системы, эта дальность не соответствует истиной и поэтому получила название псевдодальности. Координаты потребителя на основе измеренных значений псевдодальностей получают путем решения системы уравнений вида: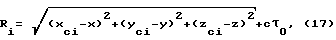
где
i=1...n - текущий номер сигнала принимаемого НКА;
n - число НКА, по которым выполняются измерения псевдодальностей;
xci, yci, zci - координаты i-го НКА в геоцентрической системе координат, вычисленные на момент проведения измерений путем решения задачи размножения эфемерид;
x, y, z - неизвестные координаты потребителя в геоцентрической системе координат;
Ri - измеренные величины псевдодальностей;
c - скорость распространения радиосигналов в вакууме равная 3•108 м/с
τ0 -
неизвестное расхождение шкалы времени потребителя с системным временем спутниковой радионавигационной системы.
Система уравнений (17) содержит 4 неизвестных и для ее однозначного решения необходимо принять сигналы не менее 4-х НКА. Способы решения таких систем рассмотрены, например, в [В.С. Шебшаевич, П.П. Дмитриев, Н.В. Иванцевич и др. Сетевые спутниковые радионавигационные системы./ Под ред. В.С. Шебшаевича. - М.: Радио и связь, 1993, с. 230 - 231].
Для определения угловой ориентации объекта вычислительный процессор 11 производит оптимальную оценку начальных фаз сигналов, принятых антенно-приемными устройствами на основе значений корреляционных интегралов I и Q, накопленных на измерительном интервале по формуле: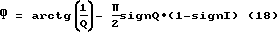
где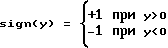
Ф - начальная фаза принятого сигнала в диапазоне однозначных измерений (-π,+π).
После оценки начальных фаз сигналов, принятых каждым из антенно-приемных устройств вычисляют значения фазовых сдвигов сигналов принятых двумя пространственно разнесенными антеннами ϕi по каждому из спутников, которые в дальнейшем используются для определения углового положения осей измеряемого объекта путем решения вышеприведенных систем уравнений для 1-4 вариантов реализации способа.
Моделирование способа производилось при следующих исходных данных:
количество радионавигационных сигналов космических аппаратов глобальной навигационной спутниковой системы ГЛОНАСС:n = 6;
число проведенных измерений m=300, что соответствует интервалу измерений 5 мин., проводимых с дискретностью 1 с;
расстояние между антеннами B = 2 м;
погрешность измерения фазовых сдвигов принятых сигналов σϕ = 1o.
Координаты космических аппаратов были получены путем решения задачи размножения эфемерид, содержащихся в кадре оперативной информации принятых сигналов.
В результате моделирования были получены следующие значения погрешностей оценки угловой ориентации и расстояния между антеннами.
В таблице проиллюстрированы погрешности оценки расстояния угловых координат объекта и расстояния между антеннами для различных вариантов реализации способа. Значения, приведенные в таблице, могут изменяться в зависимости от угловой ориентации объекта и взаимного расположения НКА.
Как видно из таблицы, применение вариантов 2, 3, 4 приводит к снижению погрешности оценки угловой ориентации в 5 - 6 раз по сравнению с известным способом. Наименьшую погрешность имеет вариант 1, выполняющий оценку угловой ориентации с погрешностью, в 10 раз меньшей чем в известном способе.
Экспериментальные исследования подтвердили полученные результаты.

Изобретение относится к спутниковой навигации и может использоваться для определения углового положения объектов в пространстве или на плоскости. В предлагаемом способе определение угловой ориентации объекта осуществляют по измерениям фазовых сдвигов радионавигационных сигналов космических аппаратов двумя и более антенно-приемными устройствами, расположенными параллельно одной или двум осям объекта. Технический результат заключается в том, что определение ориентации неподвижного объекта при заданном времени измерения осуществляется с минималной погрешностью. 1 табл., 1 ил.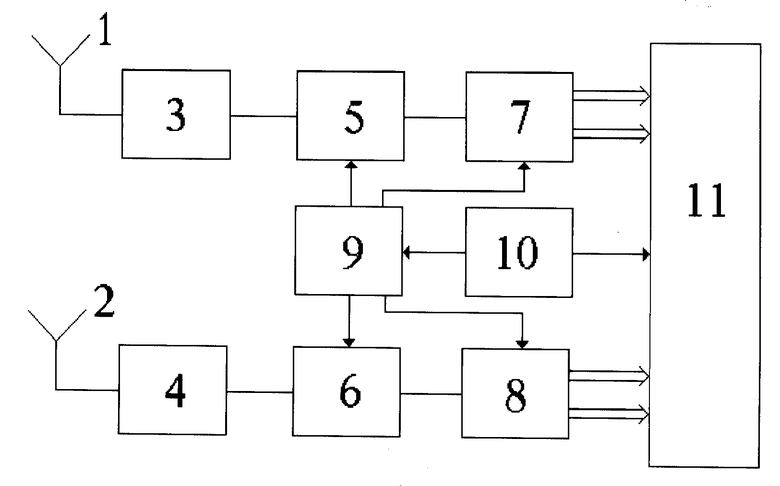
Способ угловой ориентации объекта по радионавигационным сигналам космических аппаратов, основанный на приеме сигналов от n космических аппаратов двумя или более антенно-приемными устройствами, расположенными параллельно одной или двум осям объекта, выделении сигнала с частотой Доплера, определении набега фаз за интервал времени измерения и определении углового положения объекта, отличающийся тем, что в течение интервала времени измерения производят m измерений фазовых сдвигов между парами антенно-приемных устройств, а угловое положение объекта определяют путем решения следующей системы уравнений: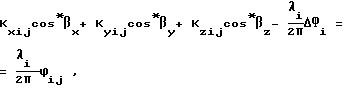
где i=1..., n - текущий навигационный космический аппарат (НКА), сигнал которого принимается;
j=1,..., m - текущее измерение фазовых сдвигов сигналов n НКА;
cos*βxyz = B•cosβxyz - произведение неизвестной базы В (расстояния между антенно-приемными устройствами) на ее направляющие косинусы cosβxyz , подлежащие определению; Kxij, Kyij, Kzij - направляющие косинусы направлений потребитель - i - тый НКА; λi - длина волны сигнала i-го космического аппарата; ϕij - измеренное значение разности фаз сигналов i-го НКА, принятых антеннами потребителя в j-м измерении; ΔФi - систематическая погрешность измеренной разности фаз, обусловленная разным временем прохождения сигналов в каналах приемоиндикатора и неоднозначностью, вызванной тем, что расстояние между антеннами превышает длины волн принимаемых сигналов.
| СПОСОБ ОПРЕДЕЛЕНИЯ КУРСОВОГО УГЛА И КООРДИНАТ МЕСТОПОЛОЖЕНИЯ ОБЪЕКТОВ ПО РАДИОНАВИГАЦИОННЫМ СИГНАЛАМ КОСМИЧЕСКИХ АППАРАТОВ | 1992 |
|
RU2022294C1 |
| RU 94018148 A1, 20.03.96 | |||
| RU 94031143 A1, 27.08.96 | |||
| US 4161730 A, 17.07.79 | |||
| DE 3305478 A, 15.09.83 | |||
| DE 4340955 A, 09.06.94 | |||
| DE 4411720 A, 06.10.94 | |||
| Лукин В.Н., Мищенко И.Н., Новиков И.А | |||
| Использование системы для определения угловой ориентации объектов, - Зарубежная радиоэлектроника, N 1, 1991. | |||
Авторы
Даты
1998-11-20—Публикация
1997-05-15—Подача