Изобретение относится к машиностроению и может быть использовано в отраслях техники, где применяются сосуды, работающие под давлением.
Известны цилиндрические оболочки эллиптического сечения, работающие под действием равномерно распределенного внутреннего давления [1], уравнение направляющей поверхности которых можно описать уравнением эллипса.
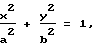 ,
,
где
X, Y - координаты направляющей поверхности в прямоугольной декартовой системе координат;
a, b - полуоси эллипса.
Известен сосуд давления, содержащий цилиндрическую обечайку и гладкосопряженные с нею днища, по крайней мере одно из которых представляет собой оболочку вращения, состоящую из сферической центральной и периферийных частей, плавно соединенных по меридиану с цилиндрической частью, причем периферийная часть днища выполнена в виде оболочки вращения с непрерывно изменяющимся радиусом кривизны меридиана от наибольшего на линии сопряжения ее со сферической частью до наименьшего на линии сопряжения с цилиндрической обечайкой [2].
Известен также сосуд давления, содержащий цилиндрическую обечайку и гладкосопряженные с нею днища [3], геометрическая форма которых задана уравнением эллипсоида [4]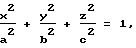 ,
,
где
X, Y, Z - координаты поверхности днища в прямоугольной декартовой системе координат;
a, b - полуоси эллипсоида, равные радиусу цилиндрической обечайки;
c - полуось эллипсоида, равная длине днища.
Недостатком приведенных аналогов является неполное использование объема в отведенных ему габаритных размерах (длина, высота, ширина).
Наиболее близким аналогом, выбранным в качестве прототипа, является сосуд давления, описанный в источнике [2].
Основной задачей разработки является создание сосуда давления с максимально выбранным объемом в заданных габаритных размерах.
Целью изобретения является увеличение внутреннего объема сосуда давления при сохранении заданных габаритных размеров.
Поставленная задача и указанная цель изобретения достигается тем, что в сосуде давления, содержащем обечайку и гладкосопряженные с нею днища, геометрическая форма его поверхности задана уравнением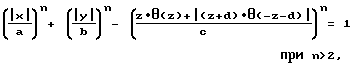 ,
,
где
X, Y, Z - координаты поверхности сосуда давления в прямоугольной декартовой системе координат;
θ(...) - функция Хевисайда;
a - половина ширины обечайки (2a - ширина обечайки);
b - половина высоты обечайки (2b - высота обечайки);
c - длина днища;
d - длина обечайки.
Отличительной особенностью предлагаемого технического решения является новая форма поверхности сосуда давления, задаваемая вышеописанным уравнением.
Указанная отличительная особенность сосуда давления является существенным признаком, так как направлена на решение поставленной задачи и достижение нового положительного эффекта в соответствии с целью изобретения.
Наличие нового существенного признака, отличающего предлагаемое техническое решение от прототипа, позволяет сделать вывод о соответствии его критерию "новизна".
Единая совокупность нового существенного признака с общими известными позволяет получить новый положительный эффект, является результатом научно-исследовательской работы и творческого вклада.
Указанная совокупность признаков неизвестна в данной области техники, что позволяет сделать вывод о соответствии нового технического решения критерию "изобретательский уровень".
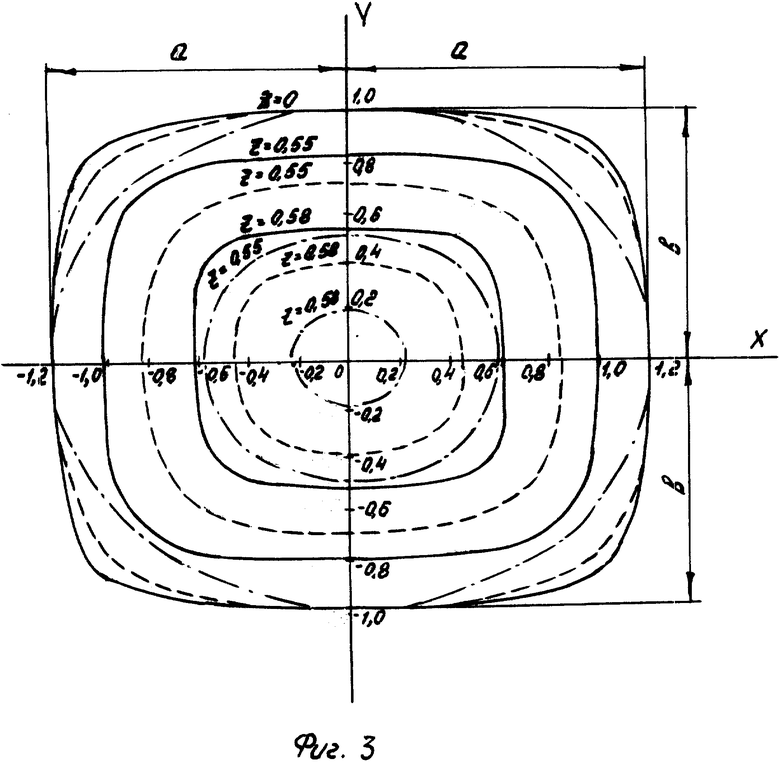
На фиг. 1 показан продольный разрез предлагаемых сосудов давления, геометрическая форма поверхности которых задана уравнением с показателями степени n = 2; 3; 4; на фиг. 2, 3 - поперечные сечения тех же сосудов давления при значении Z = 0; 0,55; 0,58; на фиг. 4 - график зависимости внутреннего объема обечаек (штриховые линии) и днищ (сплошные линии0 от показателей степени n. Сосуд давления содержит обечайку 1, днища 2 и 3. Геометрическая форма его поверхности задана уровнем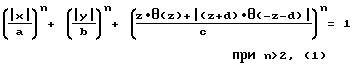 ,
,
где
X, Y, Z - координаты поверхности сосуда давления в прямоугольной декартовой системе координат;
θ(...) - функция Хевисайда;
a - половина ширины обечайки (2 • a - ширина обечайки);
b - половина высоты обечайки (2 • b - высота обечайки);
c - длина днища;
d - длина обечайки.
При увеличении показателя степени n более полно используется внутреннее пространство гипотетического прямоугольного параллелепипеда со сторонами 2 • a, 2 • b и 2 • c + d, описанного около сосуда с поверхностью, соответствующей предлагаемому решению.
Результатом использования уравнения (1) является получение сосуда, содержащего обечайку с некруговой цилиндрической поверхностью и квазиэллипсоидальные, гладкосопряженные с обечайкой днища.
На фиг. 1 - 3 показано влияние на геометрию сосуда давления показателя степени n на примере его значений 2, 3 и 4 при c = 0,6 и b = d = 1; на фиг. 2 a = 1; на фиг. 3 a - 1,2. На графиках фиг. 1 - 3 сплошными линиями приведены кривые при показателе степени n = 4; штриховыми - при n = 3; штрихпунктирными - n = 2.
Рассчитанные значения объема при изменении показателя степени n от 2 до 4 для обечайки и днищ с параметрами фиг. 1 - 3 приведены на графике показанном на фиг. 4, из которого видно, что с увеличением показателя степени n до 4 внутренний объем днищ увеличивается на приблизительно 15%, а обечайки на приблизительно 12% по сравнению с аналогами.
Увеличение показателя степени n и различия между a, b и с приводят к увеличению разницы между радиусами кривизны в сечениях и, как следствие, к различию в них напряжений под действием внутреннего давления, создаваемого в сосуде. Необходимые толщины для обеспечения прочности рассматриваемого сосуда под действием давления могут быть определены при помощи, например, конечноэлементного расчета.
Данное техническое решение позволяет максимально увеличить внутренний объем сосудов давления при сохранении заданных габаритных размеров, повысить вместимость складских помещений и сократить затраты при транспортировке за счет снижения количества транспортных средств, что соответствует критерию "промышленная применимость" т.е. уровню изобретения.
Источники информации
1. Лизин В.Т., Пяткин В.А. Проектирование тонкостенных конструкций. М.: Машиностроение, 1985, с. 203.
2. Авт. св. СССР N 1227901, кл. F 17 C 1/00, 1984, (прототип).
3. Лизин В.Т., Пяткин В.А. Проектирование тонкостенных конструкций. М.: Машиностроение, 1985, с. 132, рис. 65а.
4. Каазик Ю.Я. Математический словарь, Таллин. - Валгус, 1985, с. 275.
| название | год | авторы | номер документа |
|---|---|---|---|
| АВИАТРАНСФОРМЕР | 2010 |
|
RU2444445C1 |
| АВИАТРАНСФОРМЕР | 2012 |
|
RU2519307C1 |
| ТРУБА-ОБОЛОЧКА ИЗ КОМПОЗИЦИОННОГО МАТЕРИАЛА | 2009 |
|
RU2434748C2 |
| СОСУД ДАВЛЕНИЯ | 1989 |
|
RU2019775C1 |
| СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ | 1998 |
|
RU2159201C2 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО ОБЪЕМНОГО ИЗМЕРЕНИЯ ВЕКТОРНОЙ ФУНКЦИИ МАГНИТНОЙ ИНДУКЦИИ НЕОДНОРОДНО РАСПРЕДЕЛЕННОГО В ПРОСТРАНСТВЕ И ПЕРИОДИЧЕСКИ ИЗМЕНЯЮЩЕГОСЯ ВО ВРЕМЕНИ МАГНИТНОГО ПОЛЯ | 2012 |
|
RU2490659C1 |
| ВИБРАТОРНАЯ АНТЕННА | 2014 |
|
RU2571156C2 |
| КОНТЕЙНЕР-ЦИСТЕРНА | 1997 |
|
RU2115606C1 |
| Способ определения формы эталона поверхности сварного шва | 2018 |
|
RU2709177C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО ОТРАЖАЮЩЕЙ ПОВЕРХНОСТИ | 1993 |
|
RU2072528C1 |


Сущность изобретения: сосуд давления содержит обечайку и днища. Геометрическая форма его поверхности задана следующим уравнением: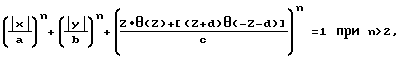
где x, y, z - координаты поверхности сосуда давления в прямоугольной декартовой системе координат, θ - функция Хевисайда, а - половина ширины обечайки, b - половина высоты обечайки, c - длина днища, d - длина обечайки. 4 ил.
Сосуд давления, содержащий обечайку и гладкосопряженные с нею днища, отличающийся тем, что геометрическая форма его поверхности задана уравнением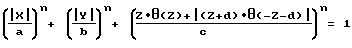
при n > 2,
где X, Y, Z - координаты поверхности сосуда давления в прямоугольной декартовой системе координат;
θ(...) - функция Хевисайда;
a - половина ширины обечайки (2a - ширина обечайки);
b - половина высоты обечайки (2b - высота обечайки);
c - длина днища;
d - длина обечайки.
| Лизин В.Т., Пяткин В.А | |||
| Проектирование тонкостенных конструкций | |||
| - М.: Машиностроение, 1985, с.203 | |||
| SU, Авторское свидетельство, 1227901, кл | |||
| Печь для сжигания твердых и жидких нечистот | 1920 |
|
SU17A1 |
Авторы
Даты
1998-04-20—Публикация
1994-06-08—Подача